一种基于再入飞行器的单平台无源定位技术

孙瑞祺，孟 刚，高志勇，高 路，李 虎

（1. 北京航天长征飞行器研究所，北京，100076；2. 空军驻航天一院军事代表办公室，北京，100076）

0 引 言

随着无源定位技术的发展，可用于定位的观测量已经从简单的来波方向向着复杂的脉内信息发展。由多种观测量和多种体制构成的无源定位系统相继出现。在系统定位精度不断提高的过程中，对定位环境的要求也在逐渐降低。对于一些成本较高，平台数量较少，要求稳定性高的平台，单平台无源定位技术有着广泛的应用前景。

传统的测来波方向单平台无源定位系统虽然算法技术成熟，简单易行，但是结构要求高，需要侦察平台提供额外的测向硬件设备，平台兼容性较差，很难在再入飞行器等结构尺寸要求较高的平台使用。因此，通过一些较易获得的其它脉冲描述字实现单平台无源定位是无源定位中重要的研究方向。

针对卫星装置平台，文献[1]、[2]中提出并详细介绍了一类基于质点运动学的单平台无源定位体制。这类技术体制已经运用到一些实际装备中，并取得了良好的定位侦察效果。

质点运动学无源定位技术是通过目标与侦察平台间的相对运动学信息对接受到的脉冲描述字的影响实现对目标的定位。在平台实际运动中通过多次侦收信号形成一组虚拟多平台。基于单平台运动合成多平台的思想，以及文献[2]中研究的频差无源定位技术，本文研究了一种基于运动学原理的频差单平台无源定位体制在高速再入飞行装置中的应用。此处的频差是指不同时刻观测平台所接收到辐射源信号的多普勒频率之差，是平台较易获得的脉冲描述字。当运动平台与目标辐射源之间存在相对运动时，频率的变化信息可以反应这种运动，用于定位[2]。即：

式中rV为辐射源与平台间的相对速度；λ为波长；f∆为信号的多普勒频率。

频差无源定位方法可以分为短基线与长基线两类。相较于将多个接收机安装在同一侦察装置的短基线侦察定位方法，将多个接收机安装在不同侦察装置的长基线频差定位具有较好的定位精度和发展前景。然而，在多平台频差定位时，需要使用的平台数量众多，各平台接收机的频率基准一般是不一致的，从而使得频差测量值有偏差。本文针对单平台高速再入飞行器进行仿真研究。在短测量时间间隔内，飞行器侦收位置之间可以拉开很长的基线，实现单平台合成长基线的频差无源定位侦察[3]。

1 定位模型

本文研究的单平台频差定位系统是针对高速再入空间飞行装置设计分析的。平台每隔一段时间对辐射源的辐射信号进行接收分选与脉内信息分析。通过一段时间的3次侦收，将3次定位侦收的位置记录下来。平台将融合3次观测的信号、平台位置、速度等参数，估计出第1次与第2次观测的多普勒频率差、第3次与第1次观测的多普勒频率差，然后结合地球表面的约束条件，解算出辐射源的位置，实现单平台合成多平台的频差无源定位。

本文在地心地固标系下推导单平台频差无源定位公式。单平台运动频差定位如图1所示。由图1可知，该坐标系下，各坐标轴与地球固定连接；Z轴与地球的自转轴重合，X，Y相互垂直并固定在赤道平面上，X轴由地心向外指向格林尼治子午圈与赤道的交点，Y轴与X，Z轴成右手关系。辐射源默认存在于地球表面上，平台距地球表面有一定高度[4]。

图1 单平台运动频差定位示意Fig.1 Schematic Diagram of Single Station Location

在平台运动过程中，3次观测可获得3个频率测量值。而3个频率测量值之间的差，也就是多普勒频率差在辐射源频率不变的情况下是由于径向速度不同造成的。根据此性质，建立频差观测方程，即：

式中 ( x1,y1,z1)， ( x2, y2,z2)，(x0,y0,z0)分别为第1、2、3次观测时的平台坐标位置；(x ,y,z)为待定位辐射源真实位置； R为地球半径，R=6371 km。λ为辐射源波长，λ= c /f0，其中，c为光速； f0为信号频率。

(vxi, vyi, vzi)为平台侦察时刻进行侦收时的速度。∆f2和∆f1分别是第2次测量与第1次测量和第3次测量与第1次测量平台与辐射源目标之间相对多普勒频率之差。通常辐射源位于地球表面，因此地球面也是一个重要的约束方程。

对地面或海面固定辐射源定位言，通常可以假定其海拔高度已知，即其位于一个半径已知的球面上（忽略实际的地球表面不是一个正球面的影响）。

通过式（2）可以对辐射源位置求解。由于上述方程都是非线性的，求解会相当复杂。在求解这类非线性方程组的方法中，通常的方法是采用牛顿迭代法和多级搜索2种方法。第1种迭代计算的效果依赖于初值点的选取和迭代格式的建立，可以获得数值结果；第2种方法是针对解非线性方程组的无源定位方法提出的似然函数逐级搜索法的定位解算方法[9]。2种方法均可应用于该种体制的定位解算上。

运用单平台的运动产生的虚拟多平台对目标辐射源进行定位相当于多平台直线布站情况下的无源定位。由于构型的原因，定位精度需要平台高速运动拉开基线来弥补。除此之外，该体制需要目标辐射源的信号体制在一定时间有一定的重频规律。

与传统的单平台测向定位相比，本文研究的定位体制需要额外增加速度测量信息。在实际的定位过程中，3次定位的位置信息、速度信息均由导航设备提供，存在测量误差，影响定位精度。在理论分析中一般建模为高斯白噪声信号，如式（3）所示：

式中 i=0，1，2； Ui， nUi分别为平台在第i次观测时的位置矢量观测值及噪声； Vi， nVi分别为平台在第 i次观测时的速度矢量观测值及噪声[5]。

2 误差分析

对方程组（2）中的3个式子在目标点( ),,xyz处微分，可得式（4）：

在每次侦收过程中，可认为平台速度是几乎不变的。假设各误差均值为零且它们之间互不相关，测量的协方差阵 RZ=E[dzdzT]，平台位置误差协方差阵

R =E[dsdsT]，平台速度误差协方差阵 R =E[dvd vT]，则

Sv

在地心地固坐标系中定位协方差矩阵为

因此定位误差为

式中 tr()P为矩阵的迹。

在矩阵P的左右乘上坐标转移矩阵以及其转置，可以将地固坐标系上的 GDOP值转换成大地坐标系上的GDOP值，即经度、纬度、高程来表示位置。本次仿真结果是采用地固坐标系进行的理论误差计算，再转换成大地坐标系的经度、纬度和高度表示定位误差结果。

3 运算仿真

为了更好地对各个定位影响因素进行分析，仿真分析中先假定某飞行器匀速在70 km高度飞行，飞行方向和速度不变，运动方向平行于地面。3次侦收的坐标位置分别为O0（东经101.13°、北纬21.76°）、O1（东经101.13°、北纬21.81°）、O2（东经101.13°、北纬21.86°）。辐射源信号的频率为3 GHz，频差均方根误差为100 Hz。平台位置的均方根误差为 50 m，速度误差为1 m/s。以下仿真中若无特殊指明，各仿真参数取上述默认值[6]。

3.1 平台速度对定位效果的影响

在仅改变辐射源频率和的情况下，仿真结果如图2至图4所示。图中等高线上的数字表示GDOP（定位误差几何稀释）误差和相对定位误差，即定位误差与目标到平台距离之比。定位误差曲线以侦收位置连线为轴对称。

图2 速度为2km/s的定位误差曲线Fig.2 Location Error Curve with Speed of 2km/s

续图2

图3 速度为3km/s的定位误差曲线Fig.3 Location Error Curve with Speed of 3km/s

图4 速度为4km/s的定位误差曲线Fig.4 Location Error Curve with Speed of 4km/s

续图4

由图2至图4可知：平台的速度越大，3%和5%相对定位误差线所围的区域越大，说明高精度的定位区域增大，总体定位精度越高。

3.2 辐射源频率对定位效果的影响

通过控制变量法，控制飞行器的速度恒为4 km/s。通过改变辐射源信号频率1～5 GHz，研究辐射源频率对相对定位误差曲线的影响，仿真结果如图5所示。

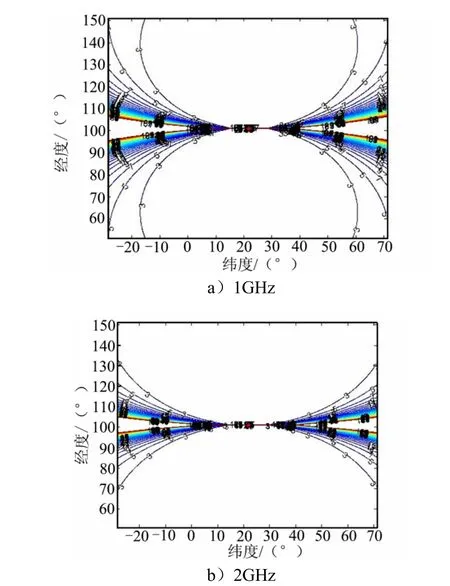
图5 相对误差曲线Fig.5 Relative Error Curve

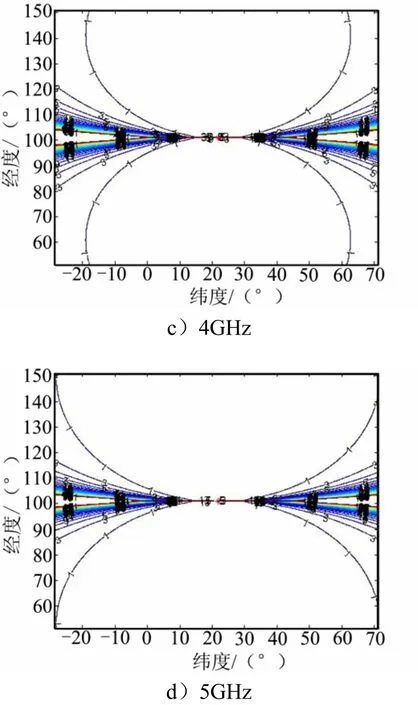
续图5

由图5可知：辐射源信号频率越大，3%和5%相对定位误差线所围的区域越大，说明总体定位效果越好。仿真结果说明单平台频差定位系统可更好地定位高频辐射源信号，而火控雷达等与武器紧密联系的有源雷达系统通常工作在高频段，从而采用该体制可实现定位，具有较好的应用前景。

3.3 平台自定位误差对定位精度的影响

单平台运动时的自定位信息与测速信息是频差无源定位中重要的输入信息。因此，此次仿真中通过控制变量法，分析自定位输入误差对飞行器定位结果的影响。自定位精度为10 m、50 m时的相对误差曲线如图6、图7所示。

图6 自定位精度为10m时的相对误差曲线Fig.6 Relative Error Curve for Self Positioning Accuracy of 10m

图7 自定位精度为50m时的相对误差曲线Fig.7 Relative Error Curve for Self Positioning Accuracy of 50m

由图6、图7可知：单平台位置自定位误差对定位性能的影响力相对较小；而单平台速度误差的影响力相对较大。这说明如果要提高单平台频差定位性能，需要采用较好的惯阻和陀螺，保证对平台的速度测量精度。

3.4 实际再入飞行器轨道的定位效果

仿真通过STK软件得到了一条再入飞行器轨迹。取轨迹中300～400 s之间的两组观测位置（观测位置用红点标出）进行了实际的误差仿真分析。每组点的位置如图8和图9所示，高度在130 km左右。仿真中的频率测量误差为100 Hz，速度测量误差为10 m/s。

图 8 实际再入飞行器第1组轨迹定位效果Fig.8 Simulation Effect of Reentry Vehicle First Group Positioning

图9 实际再入飞行器第2组轨迹定位效果Fig.9 Simulation Effect of Reentry Vehicle Second Group Positioning

从图8、图9中可以看出：在一定区域内的理论定位误差为100～200 km量级，所以该定位技术可以在很大一片区域达到3%以内的相对定位误差。

整个定位误差曲线是关于再入飞行器航迹对称的。再入飞行器的起点和落点在误差曲线中是较为特殊的点，为多条等误差曲线的交点。

4 结 论

在固定辐射源无源定位场景下，本文提出了基于再入飞行器的单平台运动合成多平台的频差无源定位体制。考虑频差偏差和辐射源频率以及自定位误差等条件下，本文分析了假想飞行器单平台频差无源定位性能，获得了若干结论，包括：a）平台运动速度越大，辐射源频率越高，定位效果越好；b）平台的自定位误差对定位效果影响不大。

通过再入飞行器的轨迹数据仿真了该种定位体制在再入飞行器上应用的可行性，绘制出了定位误差GDOP的分布图。通过误差曲线可以看出该定位体制对平台正下方的定位精度很差，无法完成定位。对运动轨迹两侧的辐射源有较好的定位效果。该体制在定位精度上不及现有的时差与频差定位系统，对平台的速度的大小以及辐射源的信号稳定性要求较高。但是，该定位体制可以实现单一再入飞行器平台对地面固定辐射源较好的相对定位效果，依然有着良好的发展和研究前景。