环形通道中湍流减阻技术及其机理研究

王春光，尤军锋，许桂阳，邓 哲，巩伦昆

（1. 西安近代化学研究所，西安，710065；2. 西安航天动力技术研究所，西安，710025）

0 引 言

有关减阻的研究可追溯到20世纪30年代但直到20世纪60年代中期，研究工作主要集中在减小表面的粗糙度上。湍流非光滑减阻技术的研究开始于20世纪70年代，并随着能源的紧缺越来越多[1]。湍流是自然界和工程技术中普遍存在的一种流动状态，降低湍流阻力对节约能源、提高效率以及消声减振等方面的研究具有十分重大的学术和实际意义。目前关于减小湍流边界层摩擦阻力的方法很多，且减阻效果均比较明显，主要包括以下3类[2]：a）壁面添加其他物质法：这类方法主要包括微气泡减阻法和表面高分子涂层减阻法2种。b）边界层控制法：对边界层的控制就是设法延缓或避免边界层的转挟，保持更大的层流区域。具体控制边界层的方法有弹性壁面法、边界层加热法以及壁面吹气和吸气法等。c）非光滑表面法：这种方法最常用的就是沟槽表面减阻法，这种方法是在表面加工条纹沟槽的方法来实现减阻目的。近年来人们对各种形状的沟槽进行了减阻性能的研究，包括矩形、T型、U型、V型以及半圆型等多种形状，都得到了一定程度上的减阻效果，大量研究结论已经表明，沟槽减阻的确是一种十分有效的减阻方法[3～10]。

本文主要研究了一种环形管道中湍流流动的结构形式。这种结构流动形式在石油工程、热交换器、涡轮机械，燃料电池、航空发动机和各种化工设备中广泛存在，对这些设备的效率产生重大影响。近些年，对于环状流的稳定性问题和介于层流和湍流状态的经典问题有诸多研究[11～14]。其中，Moradi[15,16]做了大量关于环形管道中具有顺流向沟槽的层流流动研究，分析了影响减阻效果的各种因素，包括波数、管道半径、沟槽的高度，以及不同形状的沟槽对减阻效果的影响，并分析了减阻系数的变化机理，所得结论对工程应用具有重要的参考意义。

本文主要研究环形通道中顺沟槽方向湍流状态下减阻系数的变化规律，分析其内在机理。首先将任意形状的沟槽形状表达为一阶傅里叶模式，同时建立该模式的单位化无量纲模型用来计算不同状态下的压降损失。通过Fluent流场分析软件研究不同的半径、幅值和波数对减阻系数的影响。分别分析内壁与外壁具有沟槽时对减阻系数的影响，并分析二者差别的内在原因。同时研究了内壁、外壁同时具有沟槽时的减阻特性。输出不同情况下流体速度场随几何形状的变化情况，研究流动分布的变化规律，分析影响减阻系数的内在机理。

1 计算模型和方法

1.1 计算模型

假设在一个充分发展的环形通道中，流体的流动状态为湍流状态。流体被同心内外光滑表面约束。内表面和外表面的函数表达形式分别为inr和outr，如图 1所示。

图1 单位化模型Fig.1 Unit Model

内、外表面的平均位置分别在 Rin= R 和Rout= R + 2 H，取H为特征长度，进行单位化处理。

内、外表面均为任意形状的沟槽，利用一阶傅里叶模式对其进行近似。内、外表面的函数表达式如式（1）所示：

式中inr，outr表示沟槽的几何形状；S代表沟槽的幅值；M为波的数目，MRα=，其中α为波数，量纲化模型中槽的半高R为1；ϕ为相位角。

流场分析软件Fluent中的计算模型如图2所示，为节省计算资源，建立周期对称模型。网格由ANSYS ICEM CFD 14.5生成，利用块技术生成高质量的结构化网格，且沿着壁面方向进行加密，以保证近壁面位置的计算精度，网格总数为40 000。

图2 Fluent计算网格Fig.2 Fluent Calculation Grids

对网格的有效性进行校验，输出上下壁面 y+的大小， y+均小于1，说明Fluent的自带函数可以较精确地计算近壁面的层流底层内的问题。同时为了进一步提高计算精度，结果的收敛残差设置为小于当地残差10-7，并且选取二阶迎风格式来计算所有的平衡方程。

1.2 计算方法

不可压黏性流体的RANS平衡方程如下：

本文利用商业通用流体计算软件 ANSYS Fluent 14.5对流动过程进行模拟并求解 RANS方程，选取kω- SST作为湍流模型，同时选取Low-Re correction选项。

剪切应力输运模型是标准kω-模型的一种变形形式，结合了原有kω-模型对近壁面位置的精确计算以及标准kω-模型对远离壁面位置的混合函数，涡的黏性规则被适当修改以使湍流剪切应力输运效果精确计算。

Low-Re correction选项可以对湍流的层流边界层直接计算而不必采取近似的壁面函数，因此 Low-Re correction具有更高的精度。

假设存在一种理想的牛顿流体，设其密度1ρ=，动力黏度1µ=。在单位模型中沟槽的特征尺寸取一半槽的高度为1，因此雷诺数Re可由下列公式计算：

入口边界条件为质量流率入口，由下式给出：

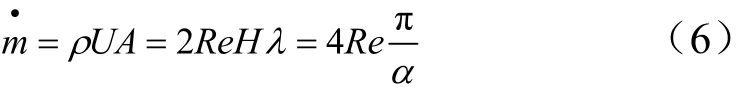
计算入口面积时需要注意，必须保证有沟槽通道的面积与光滑通道面积相等，因此对于光滑通道半径R1或 R1+ 2需根据面积相等原理进行计算修正。而对于内表面或外表面单独具有沟槽，或者双壁面都具有沟槽的情况，通道面积 A的计算公式是不同的。这里只给出最终结果，如式（7）～（9）所示。

仅有内壁具有沟槽情况下的通道面积：

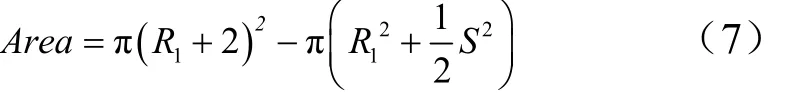
仅有外壁具有沟槽情况下的通道面积：

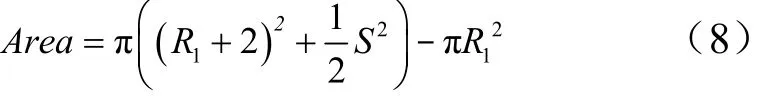
两侧都具有沟槽情况下的通道面积：

对压强及坐标进行单位化，并进行变化如下：

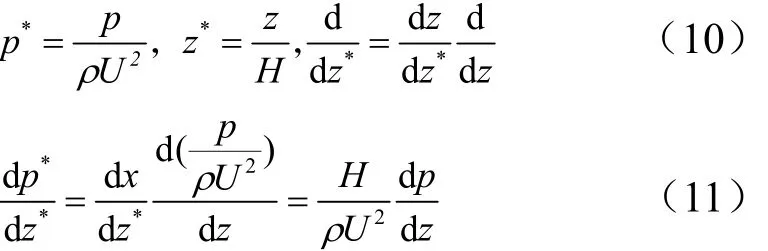
从而可得压降的计算方法如式（12）所示：

摩擦系数由式（13）求得：

将式（12）带入到式（13）中，可以得到摩擦系数计算公式如下：

式中 d p*/dz*可以直接由Fluent计算输出。

减阻系数由式（15）给出，下标“0”代表无沟槽的光滑环形通道，下标“1”代表壁面有沟槽环形通道。

式中 下标“0”代表无沟槽的光滑环形通道；下标“1”代表壁面有沟槽环形通道。

2 计算模型的校验

2.1 试验对比

Moradi[15,16]做了大量关于环形管道中具有顺流向沟槽的层流流动研究。通过公式推导，获得了环形管道具有顺向沟槽层流流动的离散化方程，结合 Matlab数值计算，得到了减阻系数随几何形状的变化规律。为了校核本文所建模型的合理性，选取相同状态下的流动参数进行流动仿真分析。计算工况为1R=2、M=5和M=10、S=0.4，与Moradi文章中的1R=1、M=5和M=10、S=0.4相对应。计算模型以及Moradi的计算结果如 图3所示（本文的计算结果只是其曲线中的2个点）。

图3 计算模型验证Fig.3 The Validation of Calculation Model

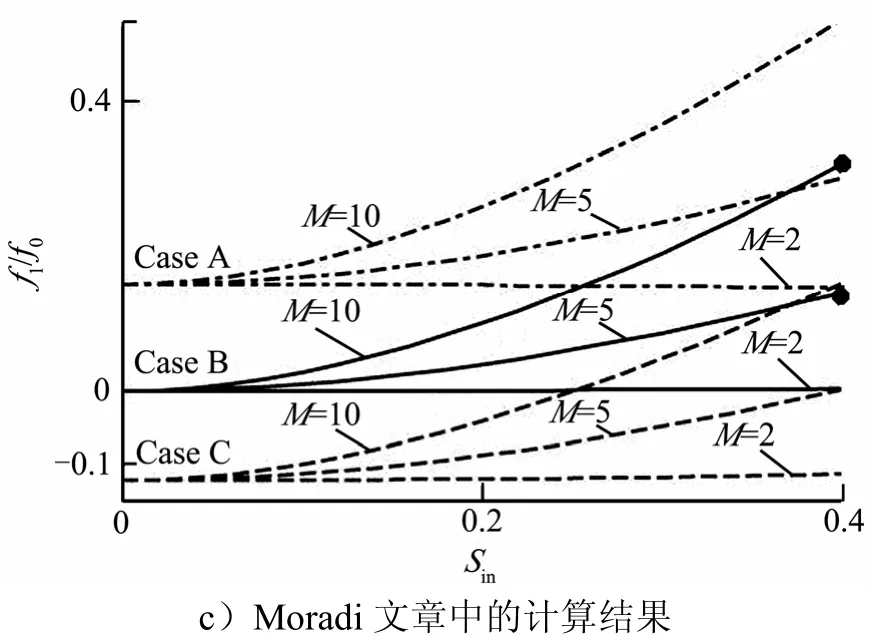
续图3

本文计算方法的计算结果分别为 f '5=0.1182和f '10=0.2927，与 Moradi的计算结果 ( f1/ f0)M=5=0.1179和(f1/ f0)M=10=0.2926非常接近，证明本文的计算模型设置合理。

2.2 与DNS结果对比

为了验证上述RANS方程ω-k SST模型在模拟湍流流动时的精度，将相同的边界条件及网格划分应用在直通道情况，与文献[16]中的直接数值模拟 DNS计算结果进行对比。由于DNS计算结果将减阻效果增加表示为相同条件下质量流率的增加，所以需要将RANS的计算结果输出为质量流率的变化。计算工况选取为幅值S=0.5，波数α分别从0.25变化到2.0的7个工况。计算结果对比如表1所示，两者的变化规律如图4所示。

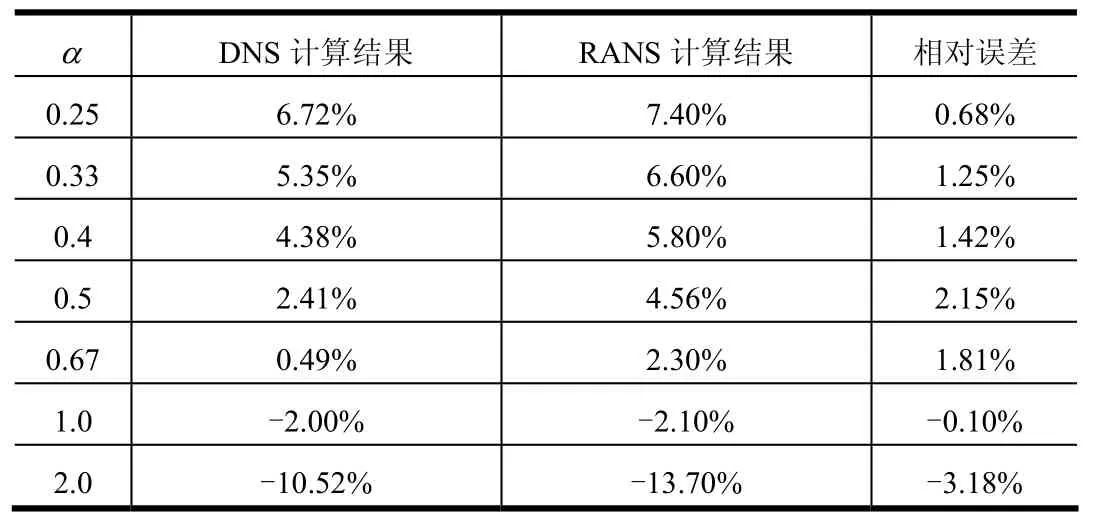
表1 RANS计算结果与DNS计算结果对比Tab.1 Comparison of DNS and RANS Results for the Change in Discharge Flow Rate for a Grooved

图4 DNS与RANS方法所得质量流率变化对比Fig.4 Plot of DNS and RANS Results for the Change in Discharge Flow Rate for a Grooved Channel

由表1和图4可以看出，RANS计算结果与DNS的计算结果变化趋势一致，最大的绝对误差仅为3.18%。在x轴的上方，即沟槽增加质量流率的情况下，RANS的计算结果略大于DNS结果；在x轴的下方，即沟槽降低质量流率的情况下，RANS的计算结果略小于DNS结果。总之，从7个点值上可以看出，RANS结果中质量流率改变的绝对值均大于DNS的结果。说明在湍流减阻预测时，应该注意RANS方法所得结果会略大。

DNS计算结果更接近实际情况，但其主要缺点是需要非常庞大的计算机内存与机时耗费，其消耗大致与3Re成正比。因此在研究雷诺数变化范围较大的湍流流动时（本文Re选取1000至30000范围内），本文研究的内容，不同几何形状模型大概上千个，需要的计算资源较多。因此当精度在可以接受的范围内时，选择RANS方法（上文已经比较），可以节省大量计算资源和时间，且能够得到合理的变化规律。

3 几何参数对减阻系数变化规律的影响

3.1 内壁具有沟槽通道减阻系数变化规律

首先计算外壁面为无沟槽光滑表面，内壁面为沟槽表面的环形通道减阻系数。内、外形面的表达式如式（16）所示：

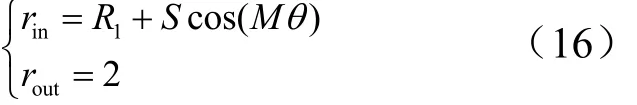
因为需要一定的压强降低才能保证驱动一定的质量流率，因此定义沿通道的压强降低即为阻力损失。而通道内径1R、沟槽的幅值S、波数RM/=α的变化都会影响压强的损失，下面分别针对不同的半径、幅值、波数进行计算，研究减阻系数随其变化规律。

Re=2648，幅值S=0.75，α由0.1变化到1.0，M由 1变化到7，计算不同状态下的减阻系数 'f，计算结果如图5所示。从图5中可以看出，波数M相同的情况下，随通道半径 R1的增加，即α逐渐降低情况下，减阻系数逐渐降低，减阻效果增加， 'f趋近一个极限值。以1=M为例，1.0→α时，环形通道的减阻系数逐渐趋近于-0.070 49。与直沟槽渠道的结果-0.070 43非常接近，如图5b所示。其他M数也可以得到相同结论，说明当R大到一定程度时，便可以忽略环形通道曲率的影响，直接借用直沟槽通道的减阻系数结果。另外从图5中也可以看出，半径R不变情况下。M数增加不利于减阻效果的降低，即M增加将会导致α增加，会降低减阻效果，这一结论与直沟槽渠道结论一致。

图5 减阻系数随几何形状的变化规律Fig.5 Drag Reduction Factor Changing with the Geometry

3.2 外壁具有沟槽通道减阻系数变化规律

研究内表面为无沟槽光滑表面，外表面为沟槽表面的环形通道减阻系数。内、外形面的表达式如式（17）所示：

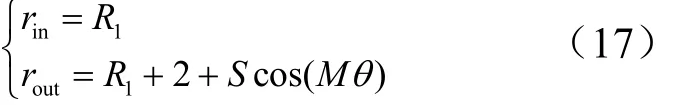
Re=2648，幅值S=0.75，α由0.1变化到1.0，M选取3个值分别为1，4，7，计算不同状态下的减阻系数 'f，将结果与内壁具有沟槽情况对比，如图6所示。

图6 减阻系数随几何形状的变化规律（外壁沟槽）Fig.6 Drag Reduction Factor Changing with the Geometry实线—内壁具有沟槽情况；虚线—外壁具有沟槽情况

从图6可以看出，在具有相同半径和波数的情况下，外壁具有沟槽情况下的减阻系数与内壁具有沟槽情况相差较小，变化趋势相同。随着半径 R1的增加，差别逐渐减小，且均趋近一个临界值。在α较小时，外壁具有沟槽情况下的减阻系数略小于内壁具有沟槽情况。分析认为，相同参数条件下，外壁沟槽情况的波数 α = M /(R1+2)略小于内壁沟槽情况下的波数α= M/R1，因此减阻系数略小，减阻效果略高。

3.3 内、外壁均具有沟槽通道减阻系数变化规律

内、外形面的表达式如式（18）所示：

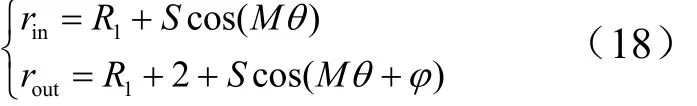
对于不同相位角ϕ对减阻系数的影响进行分析，层流状态下，当ϕ=π时可以获得最大的减阻系数，即“converging-diverging”位置[3,4,16]。同样，对于湍流状态，同样是当ϕ=π时可以得到最大的减阻系数。后续的数值计算，对于内外壁面都具有沟槽情况，都选取converging-diverging形式进行计算分析。

Re=2648，幅值S=0.75，α由0.1变化到1.0，M选取3个值分别为1，4，7，计算不同状态下的减阻系数 f '，将结果与内、外壁具有沟槽情况对比，如图 7所示。从图7可以看出，双面具有沟槽情况，可以获得更大的减阻系数，最大可以达到单壁面具有沟槽通道的3.25倍。同样，同一M数条件下，随通道半径R1的增加，即α逐渐降低情况下，减阻系数逐渐降低，减阻效果增加， f '趋近一个极限值。以M=1为例，α→ 0.1时，环形通道的减阻系数逐渐趋近于-0.2532。查看前期直沟槽渠道的结果为-0.2 523，如图7b所示。其他M数也可以得到相同结论，说明当半径大到一定程度时，便可以直接借用直沟槽通道的减阻系数结果。

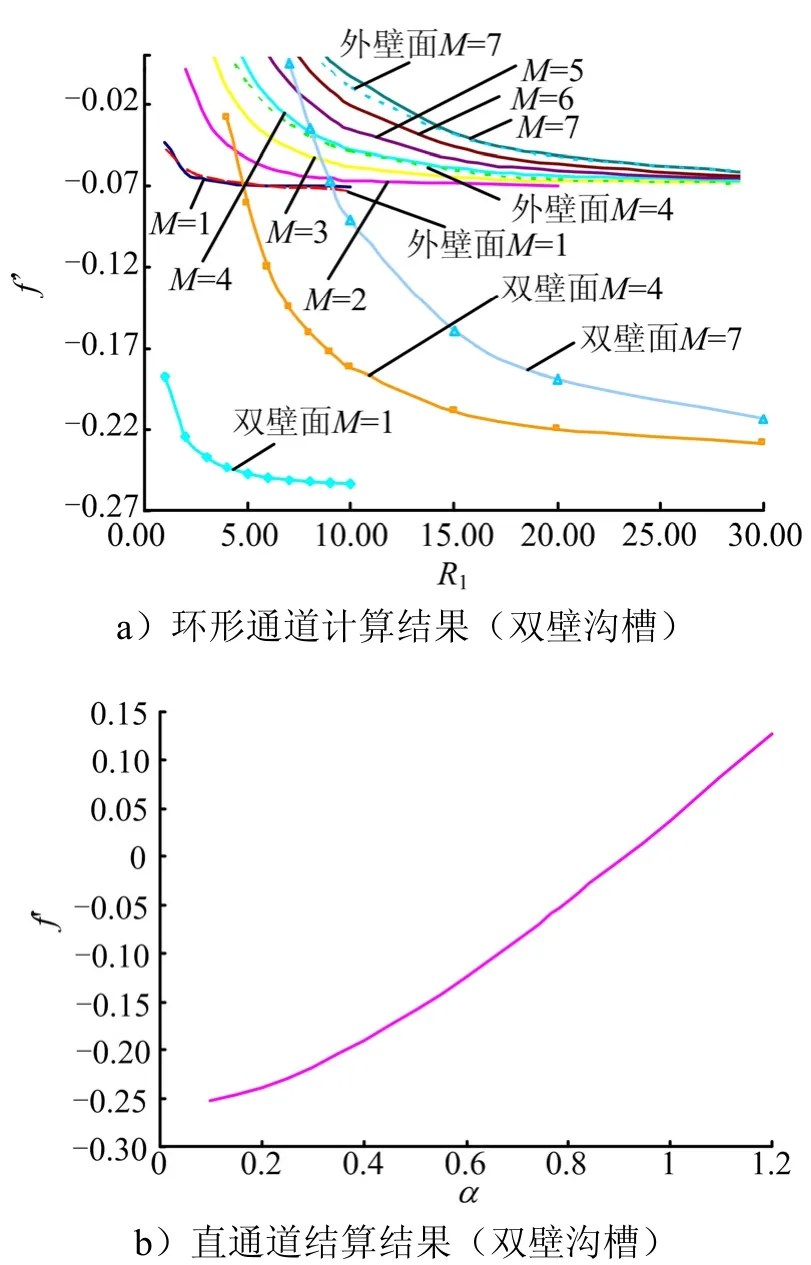
图7 减阻系数随几何形状的变化规律Fig.7 Drag Reduction Factor Changing with the Geometry

3.4 沟槽幅值对减阻系数的影响

为了研究幅值对减阻系数的影响，选取波数α=0.5的情况（M=4、1R=8），计算不同幅值S下的减阻系数，具体如图8所示。

图8 幅值对减阻系数影响Fig. 8 The Effect of Amplitude on Drag Reduction

从图 8可以看出，随幅值S的增加，减阻系数降低，通道的减阻效果增加。对于内壁面沟槽情况，f'S=1.5=-0.1054和 f 'S=0.25=-0.0151，幅值1.5可以达到幅值0.25的7倍。对于双面沟槽情况，f 'S=0.75=-0.1694和 f 'S=0.25=-0.03371，幅值0.75可以达到幅值0.25的5倍。可见，在减阻范围内，增加沟槽的幅值，更有利于增加通道的减阻效果。

3.5 不同形状沟槽对减阻系数的影响

本文对其他几种类似形式的沟槽进行了同样的计算分析，具体的几种形状如图9所示。波数（M=4）、幅值（S=0.75）、半径及边界条件均相同，计算结果如图10所示。

图9 不同形状沟槽示意Fig. 9 Different Shape Groove on Annuli

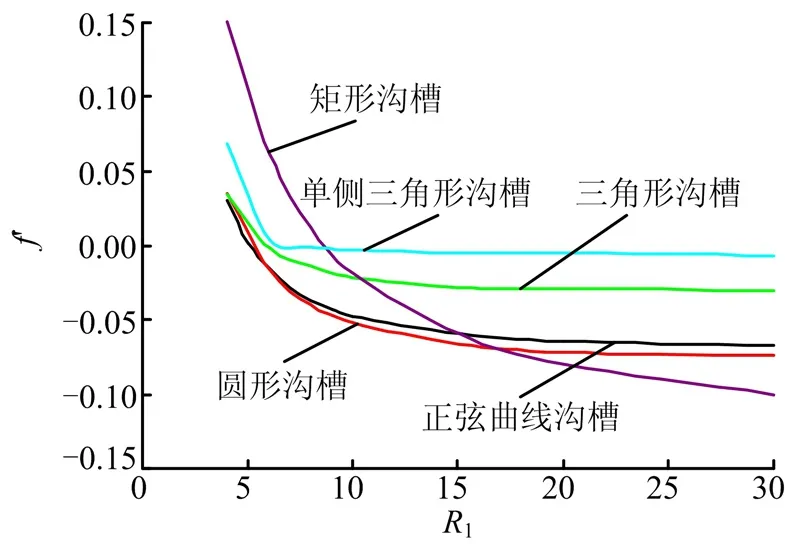
图10 不同形状沟槽下的结果Fig.10 The Results of Different Annuli with Different Shape Grooves

从图10中可以看出，单侧沟槽减阻能力最弱，图中单侧三角形沟槽曲线几乎接近X=0的轴线，随半径增加，减阻能力增加并不明显；圆形等深沟槽与正弦曲线沟槽的减阻能力相当，差别较小；三角形等深沟槽的减阻能力较正弦曲线沟槽小近1倍；矩形沟槽的减阻系数变化幅度较大，当半径较小时（约小于8），并无减阻能力，随半径增大，其减阻能力迅速增加，变化斜率大于圆形等深沟槽和正弦曲线沟槽。从方便制造加工角度讲，矩形沟槽更容易实现，但是选择这种形式时，通道的半径应该足够大（即保证波数α较小）。

4 减阻机理讨论

为了分析几何形状影响减阻效果的内在机理，将不同情况下，通道内部的流体流速输出，如图11所示，波数M=4，通道内径1R=8，幅值S=0.75。

从图11中可以看出，相比于光滑通道，由于沟槽的存在，流体的流动分布发生变化，沟槽中心速度较大，流体大部分质量流集中在沟槽中心位置，壁面位置的流速减小。对于湍流流动，近壁面位置有薄薄的附面层，剪切应力与速度变化率密切相关，可以通过式（19）求出。附面层的速度梯度变化，必然导致壁面剪应力变化。根据平衡原理，剪应力变化将导致压降变化，从而影响减阻系数变化。

式中 τ为壁面黏性层的剪切应力；µ为黏性系数；du/dy为沿y方向（与流体速度方向垂直）的速度梯度。

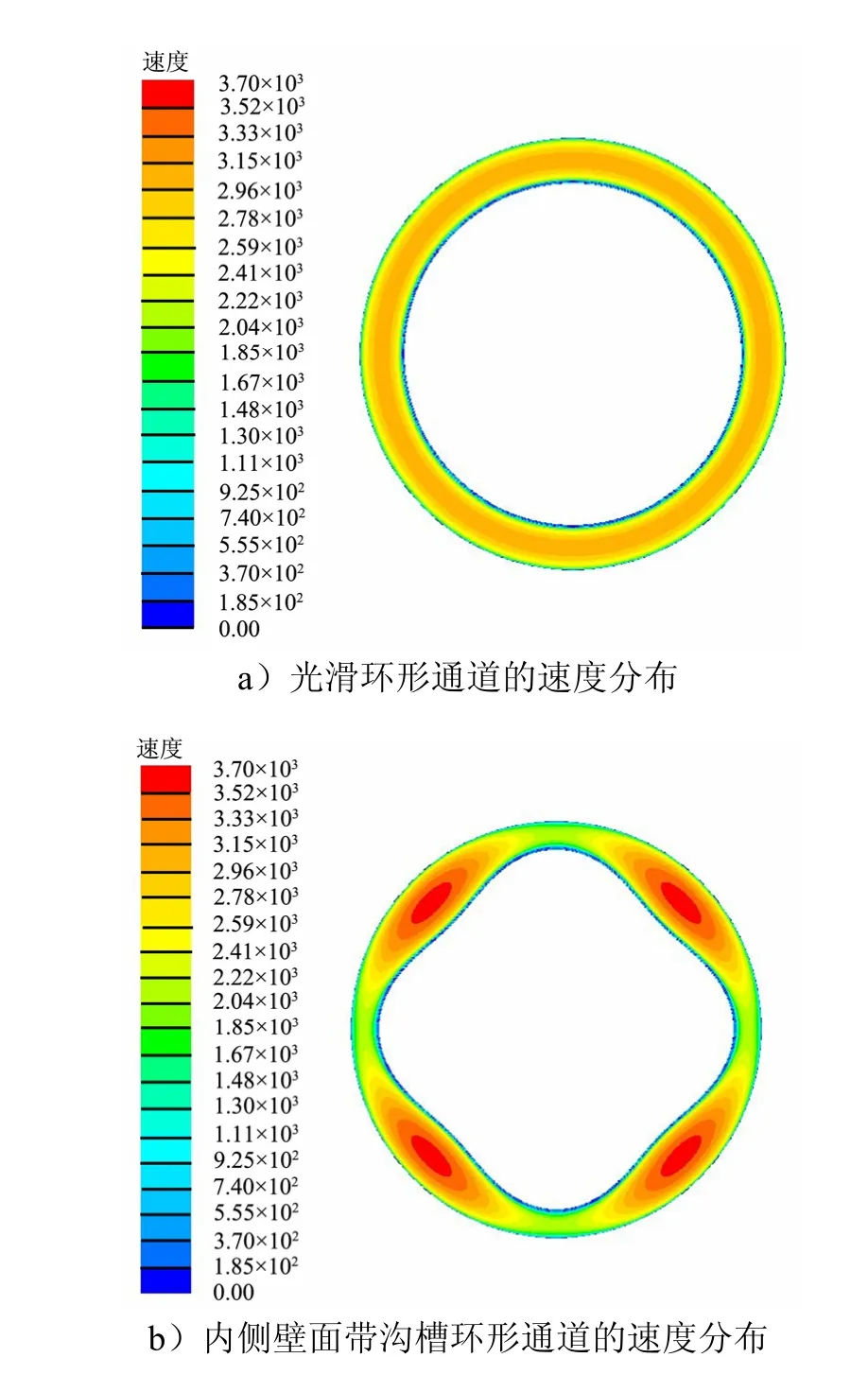
图11 通道的速度分布Fig.11 The Velocity Distribution of Annuli

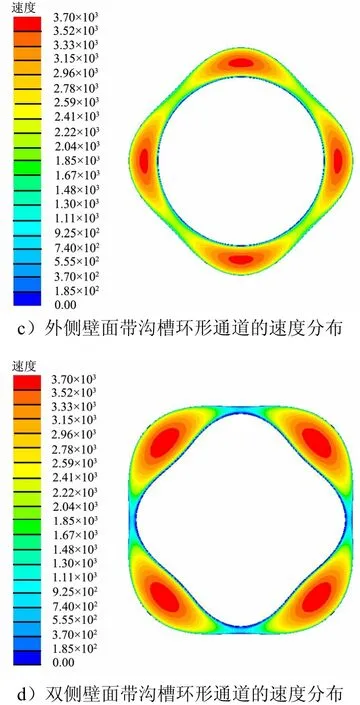
续图11

如图11b、11c所示，对于相同情况下，内、外壁面分别具有沟槽时的速度分布相似。同样根据式（19）可知，壁面的剪应力分布相似，从而压降相似导致减阻系数相差不大。对于内外壁面均有沟槽，且位置为“分离-聚合”的形式时，沟槽中心的速度明显大于一侧具有沟槽的情况，如图 11d所示，中心速度增加，流体质量流集中在中心位置，壁面附近流过的流体质量减小，黏性摩擦降低，剪应力降低将导致压降降低，减阻系数降低，沟槽的减阻效果增加。

5 结 论

a）对于环形通道，适当的增加沟槽可以实现减阻效果。相同波数情况下，随通道半径R1的增加，即α逐渐降低情况下，减阻系数逐渐降低，减阻效果增加， 'f趋近一个极限值。当R1大到一定程度时，便可以忽略环形通道曲率的影响，直接借用直沟槽通道的减阻系数结果。

b）具有相同半径 R1和波数M的情况下，外壁具有沟槽情况下的减阻系数与内壁具有沟槽情况相差较小，变化趋势相同。随着半径R1的增加，差别逐渐减小，且均趋近一个临界值。在α较小时，外壁具有沟槽情况下的减阻系数略小于内壁具有沟槽情况。分析认为，相同参数条件下，外壁沟槽情况的波数α= M /(R1+2)略小于内壁沟槽情况下的波数 α = M/R1，因此减阻系数略小，减阻效果略高。

c）双面具有沟槽情况，“分离-聚合”形式可以获得更大的减阻系数，最大可以达到单壁面具有沟槽通道的3.25倍。同样，同一M数条件下，随通道半径R的增加，即α逐渐降低情况下，减阻系数逐渐降低，减阻效果增加， f '趋近一个极限值。当R大到一定程度时，便可以直接借用直沟槽通道的减阻系数结果。

d）相比于光滑通道，沟槽将导致流体的流动分布变化，沟槽中心速度较大，流体大部分质量流集中在沟槽中心位置，壁面位置流过的流体质量减小，黏性摩擦降低。根据平衡原理，黏性摩擦剪应力降低将导致压降降低，减阻系数降低，通道的减阻效果增加。

e）对于其他形式的减阻沟槽，单侧沟槽减阻能力最弱。圆形等深沟槽与正弦曲线沟槽的减阻能力相当。三角形等深沟槽的减阻能力较正弦曲线沟槽小近1倍。矩形沟槽的减阻系数变化幅度较大，随半径增大，其减阻能力迅速增加。选择矩形沟槽时，通道的半径应该足够大（即保证波数α较小）。