货车驾驶室悬置系统性能参数优化设计

黄德惠 向建东 张吉平 耿志广 周强

（一汽解放青岛汽车有限公司，青岛266043）

主题词：悬置优化 参数识别 曲线拟合DOE设计

1 前言

货车驾驶室悬置优化设计是提升货车舒适性的关键技术，准确的仿真模型是驾驶室悬置优化设计的基础。目前，相关学者[1-6]均基于多体动力学对货车悬置系统进行建模和试验验证，但在研究过程中均未提及模型参数的校正问题，而在驾驶室悬置优化设计中，由于驾驶室前、后悬置都存在橡胶衬套，且衬套参数常常难以精确获取，同时悬置系统铰链连接处存在装配间隙和摩擦，因而模型建立过程不可避免会进行简化，这些都会对优化设计结果产生一定影响[7-10]。

针对上述问题，本文采用模态频率为目标的刚度辨识和传递函数曲线为目标的曲线拟合方法，分别修正模型的刚度和阻尼参数，获取了准确的仿真模型，并对其进行了优化设计和试验验证。

2 驾驶室悬置模型搭建

本文采用交互式建模方法,即根据元件实际尺寸通过CAD软件建立实体模型,并导入机械系统动力学自动分析软件（ADAMS）中，在ADAMS中添加力和约束并修改相关参数，最终得到完整的虚拟样机模型。

2.1 驾驶室多体参数化建模

以驾驶室悬置半浮系统为研究对象，以前悬衬套六向刚度和阻尼、后悬液压锁衬套六向刚度和阻尼和后悬弹簧减振器刚度和阻尼为设计参数变量，在ADAMS中建立驾驶室悬置系统参数化辨识模型，如图1所示。

前悬衬套六向刚度、后悬液压锁衬套刚度和后悬弹簧减振器刚度、阻尼设计参数变量设计值如表1所列。

图1 驾驶室悬置系统参数模型

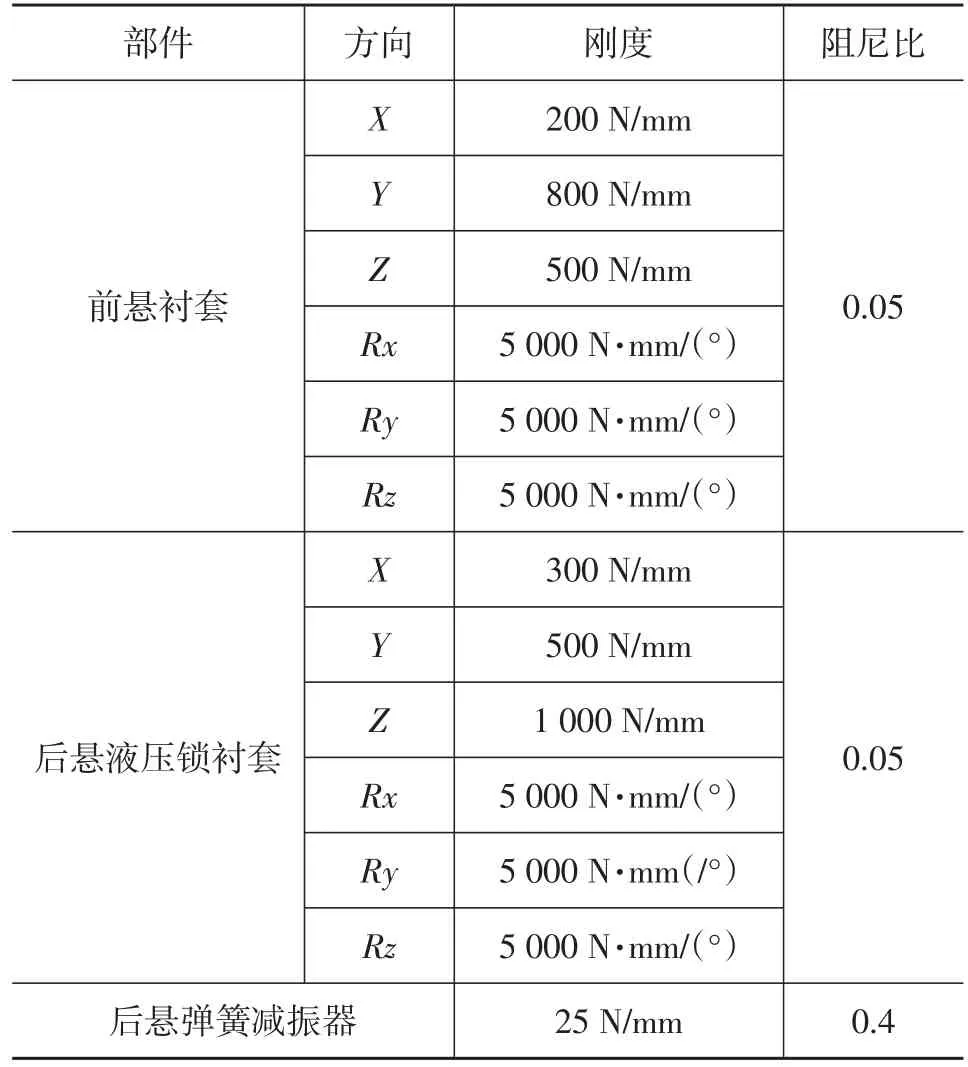
表1 设计变量参数

2.2 驾驶室悬置模态测试

驾驶室在外界激励下的振动是其各阶模态振型叠加的结果，而对振动的主要贡献来自驾驶室前几阶模态[7]。本文采用MOOG六自由度试验台架（图2）进行扫频激励来获取驾驶室六阶刚体模态（按振型分为前后、左右、上下、侧倾、俯仰、横摆等6个方向的模态），模态频率仿真结果和试验结果对比如表2所列。由表2可知，俯仰、前后与上下3个方向模态频率的仿真和试验较一致，均小于10%，但是在侧倾、横摆和左右3个方向模态频率差距较大，需要对模型相关参数进行修正。

图2 驾驶室悬置系统模态测试台架

表2 仿真模态频率与试验模态频率对比

2.3 模型修正

针对上述仿真模型不够精确的问题，根据表2的扫频试验结果，利用参数辨识的方法识别弹性件的刚度和阻尼，并将辨识刚度与设计刚度的比值称为修正系数α，将辨识阻尼比与设计阻尼的比值设为修正系数β。

2.3.1 刚度参数辨识

通过不断迭代弹性件的刚度修正系数，使ADAMS模型计算得到的模态逼近试验模态，将参数辨识通过优化设计来实现[11]。此流程利用Isight软件集成AD⁃AMS和MATLAB，采用多岛遗传优化迭代的方法，通过修改弹性元件的等效刚度，使ADAMS计算的六向频率逼近设计值，即优化目标最小，其最优结果得到的刚度修正系数即为性能设计参数，此结果为刚度辨识结果，如图3所示。

图3 参数辨识设计

将前悬衬套六向刚度、液压锁衬套六向刚度和后悬弹簧减振器刚度共计13个修正系数分别设为α1～α13，并将它们设为辨识参数。将刚体模态仿真模态频率和试验模态频率的最小差值obj作为辨识目标，则

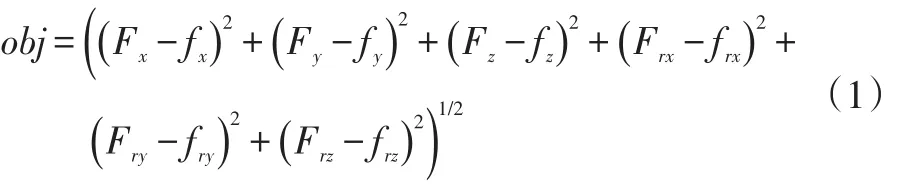
式中，obj为仿真模态频率与试验模态频率的差值；Fx、Fy、Fz分别为仿真的前后、左右、上下运动模态频率；Frx、Fry、Frz分别为仿真的侧倾运动、俯仰运动、横摆运动模态频率；fx、fy、fz分别为试验的前后、左右、上下运动模态频率；frx、fry、frz分别为试验的侧倾运动、俯仰运动、横摆运动的模态频率。

通过对刚度参数进行修正，修正系数如表3所示，得到新的仿真模态频率。刚度参数辨识后，仿真模态频率与试验模态频率对比如表4所列。

表3 刚度修正系数结果

表4 刚度辨识后模态频率结果对比

由表4可知，经刚度参数辨识后，仿真模态频率与试验频率相比误差小于10%。

2.3.2 阻尼参数辨识

经刚度参数辨识后，保证了仿真频率的准确性，为进一步提升仿真模态的准确性，要保证悬置系统传递函数曲线吻合度。

基于刚度辨识结果，对驾驶室悬置系统进行上下方向扫频仿真分析，与MOOG六自由度台架上下方向扫频结果进行对比，其传递函数如图4所示。

图4 辨识前仿真与试验传递函数曲线对比

由图4可知，上下方向模态频率一致，但仿真与试验的幅值误差较大。这主要是因为仿真模型中阻尼与实际不符合导致，故需要对前悬衬套六向阻尼比、液压锁衬套六向阻尼比和后悬弹簧减振器13个阻尼比进行辨识修正，修正系数设为β1～β13。采用Isight软件集成ADAMS和MATLAB，通过修改阻尼比使ADAMS扫频仿真传递函数曲线与MOOG试验仿真曲线不断逼近，得到阻尼修正系数。

通过传递函数曲线辨识结果，其修正阻尼比系数如表5所列，俯仰运动仿真与试验传递函数曲线对比如图5所示，仿真模型与试验模型误差均＜5%，可用于后续优化设计。

表5 阻尼比修正系数结果

图5 辨识后仿真与试验传递函数曲线对比

3 试验设计（DOE）

对半浮驾驶室舒适性进行优化设计的原理主要是优化其模态分布，使其尽量避免驾驶室与车辆其它总成产生共振,有效降低驾驶室内的振动，故需要对影响其模态分布的弹性元件参数和尺寸参数进行试验设计（Design of Experiment,DOE）。

3.1 弹性元件参数灵敏度分析

由于弹性元件相关参数对驾驶室模态的影响程度尚不明确，因此将这些参数全部作为试验因子进行分析。在试验设计中分别以前悬6向刚度、后悬弹簧刚度以及液压锁衬套6向刚度共13个因素作为研究因子。为准确分析出因子对系统的影响，试验设计中水平范围根据因子特性选取，应尽量包含因子的全局极值点。但是水平范围也要考虑系统的稳定性，不能过大造成系统失稳或不真实。通常情况下，每个因子常取2～3个水平。

因为随着因子水平的增加试验次数会激增，进而影响计算分析效率，因此每个因子选择3个水平，因子取值如表6所列。

联合Isight和ADMAS进行灵敏度分析，其流程如图6所示。

分析结果表明，对于半浮驾驶室悬置系统，前悬衬套的刚度对模态频率的影响最大，它的Z向刚度基本上决定了上下运动和侧倾运动的模态频率，Z向和Y向刚度共同决定了左右运动的模态频率。对于半浮驾驶室最重视的是俯仰运动，俯仰运动的灵敏度分析结果如图7所示，由图7可看出，前悬衬套的Z向和Y向刚度以及液压锁衬套的X向刚度、后悬弹簧减振器的刚度对俯仰运动的模态频率影响较大。

表6 设计变量刚度参数因子水平

图6 灵敏度分析流程

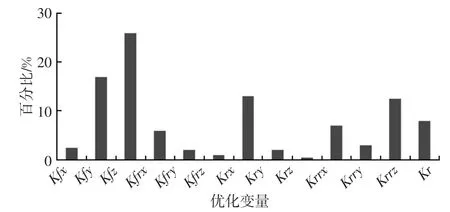
图7 俯仰运动灵敏度分析结果

3.2 尺寸参数灵敏度分析

除了弹性元件对驾驶室模态存在影响外，后悬液压锁臂横臂的长度L也对驾驶室系统模态存在影响。图8为后悬结构图，由图8可知，A点与B点的距离L即为液压锁横臂的长度，保持A点位置不动，改变B点的坐标，分别计算L为140、175、210、245和280的模态，模态频率仿真结果如图9所示。通过对比分析可以看出，随L的增大，各阶频率都有减小的趋势，其中二阶俯仰频率减小最为明显。

图8 后悬结构示意

图9 液压锁横臂长度变化对模态的影响程度

4 驾驶室悬置系统优化设计

4.1 优化模型的建立

根据前述分析结果，取前悬衬套的三向平动刚度、液压锁衬套的X向刚度、后悬弹簧减振器刚度以及液压锁臂的长度L（yB）共计6个参数作为优化变量，液压锁臂长度L取结构能实现安装的范围，以驾驶室悬置系统的前后悬置的动挠度作为约束条件，参照试验车辆的设计标准，前悬动挠度小于10 mm，后悬动挠度小于50 mm，以驾驶室座椅地板处的三向加权加速度均方根值作为整车行驶平顺性的优化目标，输入为海南采集路谱。其优化数学模型可表示为：

式中，wk为座椅地板处三向加速度均方根值；kfx、kfz、kfz为前悬衬套的三向刚度；krx为液压锁衬套的向等效刚度；kr为后悬减振器的刚度；yB为液压锁与后悬支架连接点处的y坐标；zf为前悬支架与驾驶室连接处的z坐标；zA为液压锁与减振器上部连接点的z坐标。

4.2 优化结果

采用多岛遗传算法，经过150次迭代，最优解为第82次，如图10所示。此时，驾驶室地板三向加速度均方根值为0.502 1 m/s2，则各设计变量的优化值如表7所列。

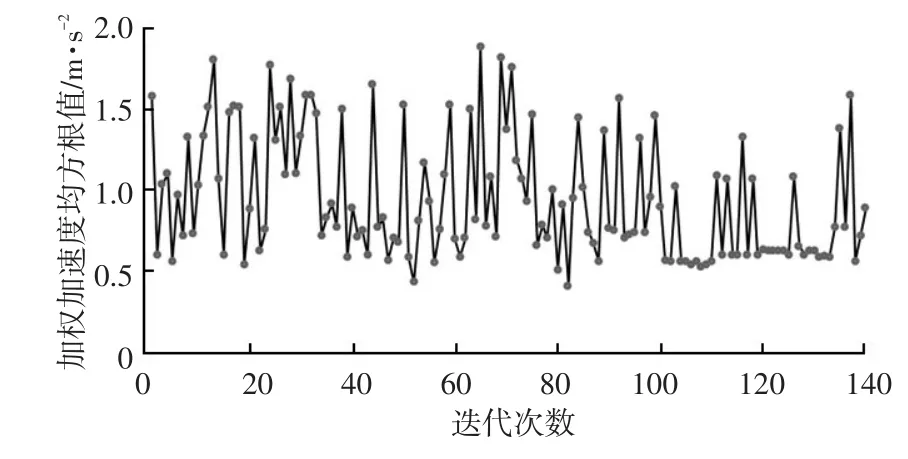
图10 目标值随迭代次数变化曲线

表7 设计变量优化结果

4.3 试验验证

利用刚度修正系数可以求出设计刚度，刚度修正结果如表8所列。

表8 设计变量修正前、后对比

对修正后优化结果进行试验验证，前悬衬套三向平动刚度X、Y、Z分别取250 N/mm、650 N/mm和400 N/mm，液压锁衬套X向刚度取250 N/mm，取后悬弹簧减振器刚度为20 N/mm，并设计新的后悬液压锁长臂，将其长度L由140 mm增长为280 mm。在6自由度台架上对原结构和新结构进行试验验证，在台架上导入50～80 km/h各车速段采集的路谱进行平顺性分析，分析结果如图11所示。通过对比可知，新悬置组合的平顺性比原悬置组合提高了20%左右，提高了驾驶室的舒适性。

图11 结构改进前、后地板平顺性对比

5 结束语

建立了驾驶室悬置半浮系统的多体动力学仿真模型，提出采用试验模态频率为刚度辨识的目标修正刚度参数，再用传递函数曲线为曲线拟合的辨识目标修正阻尼参数的方法，对仿真模型进行了修正，获取准确的等效仿真模型。进一步采用DOE试验方法，对影响模态频率的弹性性能参数和尺寸性能参数进行了灵敏度分析，并对影响隔振性能的主因进行优化设计并进行试验验证，试验结果表明，优化后的驾驶室地板平顺性提升了20%，该方法合理有效，对其它悬置结构设计具有借鉴作用。