基于奇异值分解法对某矿用自卸车驾驶室平顺性的试验研究

马 娜,周新涛

(1.陕西同力重工股份有限公司 研发中心,陕西 咸阳 712000; 2.西安汽车科技职业学院 机械工程系,西安 710600)

随着矿山开采机械设备大型化的发展,矿用运输车辆的承载量和车辆悬置系统的刚度也均在增大,导致驾驶室的振动情况加剧,使其驾乘舒适性变差[1].人体若长时间暴露在这种环境中,就会影响车辆驾驶的稳定性，降低工作效率,甚至导致事故的发生[2-3].故在这种情况下,对驾驶室悬置系统隔振性的研究就显得尤为重要.而矿用自卸车驾驶室悬置系统各结构件的布置位置较为紧凑,采用改变悬置系统的结构形式难以实现减振的目的.通常情况下,为悬置系统的刚度和阻尼等参数进行合理的匹配,可以改善其减振效果[4].但是,这要经过复杂的理论计算才能获得较为理想的结果,且理论值与实测值存在误差,将会导致驾驶室悬置系统的减振性达不到预定的效果.

目前,对矿车自卸车驾驶室悬置系统减振性研究,最准确的方式是矿区实车试验法[5-6].而矿区的工作环境非常恶劣,试验测得的数据受到了各种激励源的干扰,使得振动特征提取的难度大大增加,因此，对试验数据需要进行降噪处理.在实际应用中,信号降噪的方法有很多[7-9],而每种降噪方法都有特定的局限性.本文结合矿用自卸车的运行情况和驾驶室悬置系统的结构特点[10],采用奇异值分解[11](Singular Value Decomposition,SVD)法对试验信号进行降噪预处理.该法不存在相位延迟的现象,且具有较好的稳定性、旋转不变性和比例不变性等优点,能得到较好降噪效果.

1 振动特征分析理论

本节对振动数据降噪分析的方法进行简单介绍,为后续矿用自卸车驾驶室悬置系统振动实测信号的预处理及悬置振动特征研究作基础.

1.1 SVD理论

SVD的实质是将实测信号进行正交变换,对信号中的高频随机噪声有很好的过滤效果,其变换关系式为

(1)

SVD法所得到的矩阵奇异值,具有唯一性、稳定性和比例不变性等性质.奇异值降噪的关键因素是确定重构相空间的阶数和矩阵重机分离阶数.

1.2 奇异值差分谱

由式(1)计算出信号矩阵H的奇异值σ,为了描述相邻两奇异值与谱值变化序列的变化关系,在本节处引入奇异值差分谱(Singular Values Difference Spectrum)D的计算关系式为

(2)

式中:i=1,2,…,r-1.

由式(2)计算出整个时间序列中的差分谱值,其奇异值差分谱序列为

(3)

1.3 奇异值重构阶数的确定

由SVD降噪原理将振动信号构建一个Hankel矩阵,按式(1)计算出整个时间序列上的奇异值.再根据式(2)和式(3)计算出奇异值差分谱值,按照

(4)

就能得出奇异值差分谱序列的峰值谱N,以及相应的重构阶数.如差分谱峰值dk,以角标数字k找出奇异值序列中的对应峰值σk,即在k值前的奇异值变化较大,而之后的奇异值将接近于某一值后稳定.说明峰值σk是信号与噪声的分界点,此时取k值前的奇异值重构信号,该信号就是降噪处理后的真实振动特征数据.

2 SVD法降噪仿真分析

为了验证SVD法的可靠性,采用一组含有高斯脉冲信号和随机信号等噪声信号进行试验仿真,其仿真信号y(t)为

(5)

式中:v(t)=cos(2π15t)为无噪声的真实信号;n(t)为随机信号,其均值为0,方差为0.6;e(t)为高斯脉冲信号.

采用采样频率为2 000 Hz、采样点数为1 000个样本来进行仿真模拟,其模拟信号y(t)的时域波形如图1所示.真实信号与含噪声信号相比,真实信号受到了复杂的干扰,如图1(b)时域曲线图上的毛刺状干扰信号,增加了真实特性提取的复杂程度.

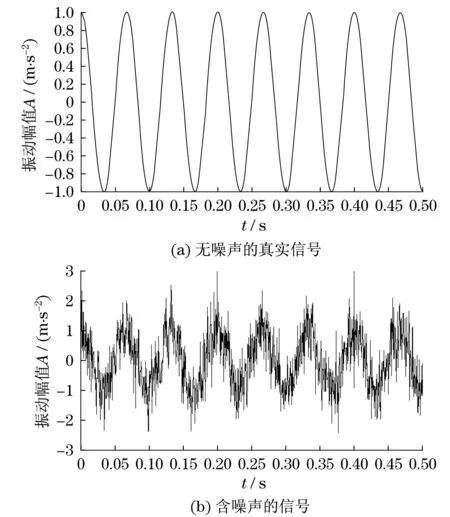
图1 振动信号的时域图Fig.1 Time-domain graph of vibration signals

将图1(b)中含噪声的振动信号进行SVD,得出如图2所示的奇异值及奇异值差分谱曲线图.由图2可以确定,奇异值重构相空间的阶数为2.然后,在该相空间内将奇异值进行重构,得出降噪后的信号,如图3所示.从图3中可以看出，降噪后的信号与无噪声干扰的真实信号,其频率、幅值等基本相同.由此可见,采用SVD法对含有噪声的信号有很好的降噪效果.

图2 奇异值与差分谱曲线图Fig.2 The graph of singular value and difference spectrum

图3 降噪后的振动信号Fig.3 The vibration signals after noise reduction

3 道路测试及结果分析

3.1 实车测试

根据矿用自卸车的运行特点及国家试验标准[12-13]设置本次试验,并按照矿用自卸车在矿区常用的运行速度,试验车速分别选择10,20,30,40 km/h 4种.路面激励向上传递到驾驶室时,座椅悬置系统是最终的减振装置，且座椅面直接与人体接触,此处的振动能量将会直接作用到人体.故本次对驾驶室平顺性研究,主要集中在驾驶室座椅处的测点上(座椅坐垫处),试验条件如表1所示.

表1 试验条件Tab.1 The test conditions

测点分别布置在板簧、车架、驾驶室悬置、驾驶室地面(脚垫)和座椅支撑面(座垫)等位置处(见图4).在每个工况下分别进行两次测试,以确保测试后获得的信号正常有效,其试验场地如图5所示.

图4 测点布置情况Fig.4 Survey point layout

图5 试验场地Fig.5 The test site

3.2 测试数据的降噪处理

本次测试布置的测点较多,本文以矿用车最常用的速度20 km/h时座椅座垫处的振动情况为例.其时域数据如图6所示,座椅处在3轴向的振动信号受到了干扰,需要将其进行降噪处理.

依据SVD原理,将本次所测得的振动信号进行降噪处理.过滤掉噪声等干扰信号后,经过多次调整和试算,利用SVD的逆运算重构出振动相空间矩阵.该矩阵就是降噪后振动信号的最佳逼近值,如图7所示.

同理,得出座椅处在4种不同车速下奇异值差分谱的关系,如图8所示.由图8中的值,可以确定在不同车速下奇异值的重构阶数.

按照图7和图8中的计算参数,将奇异值在其相空间内重构,得出如图9所示的重构信号,即为降噪后无干扰的振动信号.

图6 20 km/h时座椅处实测振动加速度时域图Fig.6 The time-domain diagram of measured vibration acceleration in seat at 20 km/h

图7 座椅处振动信号奇异值的分布图Fig.7 The distribution of singular values of vibration signals at seat

图8 座椅处振动信号奇异值差分谱的分布图Fig.8 The distribution of singular difference spectrum of vibration signal at seat

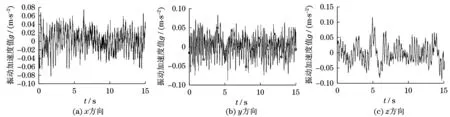
图9 20 km/h时座椅处经SVD降噪后的振动加速度时域图Fig.9 The time-domain diagram of vibration acceleration after SVD noise reduction in seat at 20 km/h

3.3 振动数据的加权均方根分析

按照国家标准[12-13],将降噪后的试验数据在数值分析软件中进行加权计算.主要为座椅处测点的x,y,z轴加速度值进行加权,其加权系数分别是1.4,1.4和1.0.得出座椅处的加权均方根值,如表2所示.

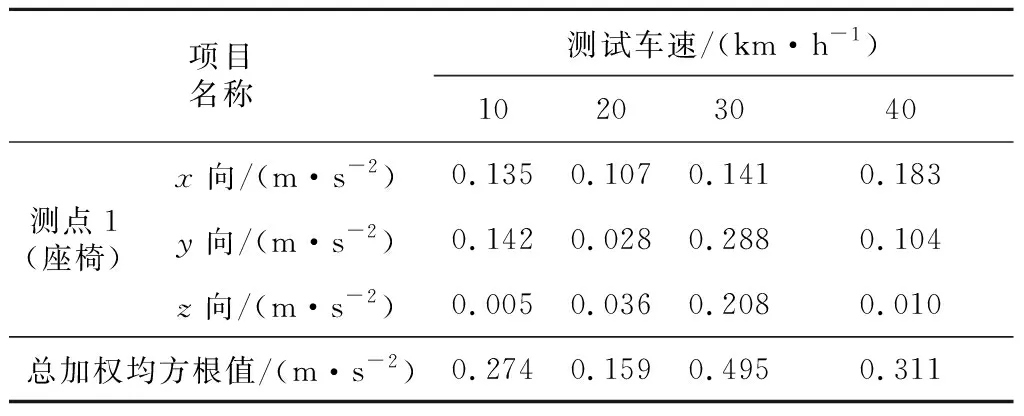
表2 座椅处的加权加速度均方根值Tab.2 Weighted acceleration mean square root value at seat

由表2得出当车速在20 km/h时,驾驶室的平顺性最好;当车速在30 km/h时,其驾驶室的平顺性最差.

4 驾驶室振动的频响分析

座椅处振动的均方根值较大,使得驾驶室的驾乘舒适性较差.将此测点处降噪后的信号进行频响分析,找出该处的振动特性.通过将其进行快速傅立叶变换(Fast Fourier Transformation,FFT)后,得出座椅处的频响特性,如图10所示.由图10可得座椅处在4种不同车速下,其主要振动频段在0～10 Hz的范围内,刚好与人体敏感频段重叠.故该类矿用自卸车在任何速度下的驾乘舒适性均不太理想,且车速为30 km/h时的舒适性最差.因此,后续需要对车辆的簧载悬架系统、驾驶室悬置系统和座椅减振系统进行优化,以降低振动幅度提升驾乘舒适性.

图10 座椅处经SVD降噪后的频响特性关系图Fig.10 The frequency response characteristics of seats reduced by SVD

5 结论

本文采用SVD法,对某型矿用自卸车驾驶室平顺性的试验数据进行降噪处理.根据SVD的基本原理,使用数值模拟方法,仿真结果表明：该法具有很好的降噪效果.同时,采用该法将矿用自卸车驾驶室座椅处的试验数据进行奇异值和奇异值差分谱分析,得出该测点处的试验数据随车速的变化规律.通过多次调整和试算,确定信号奇异值的重构阶数并对振动信号重构,得出无噪声干扰的纯净信号.最后,对座椅处进行加权均方根计算和频响分析,得出该类型车辆驾驶室的平顺性较差.指出后续需要对车辆各悬置系统进行减振优化,以提升该车驾乘的舒适性.