无迹信息滤波耦合交互式多模型的多传感器机器人轨迹控制

卢 晨,刘 正

(苏州工业园区服务外包职业学院 信息工程学院,江苏 苏州 215123)

随着工业自动化的快速发展,越来越多的机器人参与到智能制造中,特别是在搬运和传送等工作简单繁琐需要投入大量人力的岗位上,机器人发挥着重要的作用[1-2].机器人在各生产线上一旦投入使用,且需要调整新的生产线时,其原有的控制程序将需要大量的维护和编程投入,此外,在多机器人协同作业方面,对机器人位置的定位是实现协同工作的基础,因此,对机器人轨迹跟踪是机械制造行业发展的必然需求[3].

多传感器数据融合由于能从多种传感器中提取优势互补的数据,具有更高的精度和更好的鲁棒性,已广泛应用于车辆定位、组合导航、目标跟踪等工程实践中[4-5].在多传感器数据融合算法中,由于卡尔曼滤波结合信息滤波实现简单,广泛应用于处理多传感器数据.该算法能很好地处理线性系统的数据融合,但对于非线性系统效果欠佳[6-7].针对非线性系统的融合,Lee等[8]提出了无迹信息过滤器(Unscented Information Filtering，UIF),该滤波算法基于Sigma点滤波器的无迹变换方法从扩展信息滤波结构中获得,可直接对非线性系统进行处理,避免了线性化误差,能够实现多传感器估计的信息滤波器的有效性.无迹信息滤波被大量应用于非线性系统中[9-10],然而,随着传感器数量的增多,如何对多传感器之间的数据进行有效融合,提高多传感器的测量精度,成为需要研究的问题.交互多模型(Interacting Multiple Model，IMM)是用于机器人跟踪最常用的多模型算法之一[11],IMM滤波器由多个并行运行的滤波器组成,利用模型概率将每个滤波器的状态估计和协方差结合起来.数据融合与IMM滤波器的一个缺点是它不使用以前的组合估计来预测下一个状态和协方差,但这是常规信息过滤器计算信息所需要的[12].

本文利用UIF和IMM各自的优点,提出了一种基于分布式多传感器融合结构下的信息融合算法(Unscented Information Filtering and Interacting Multiple Models，UIF-IMM).该算法融合了每个由IMM滤波器组成的UIF信息,而不是IMM滤波器简单的组合估计,融合的信息不仅是信息状态贡献和信息矩阵,而且是模式似然函数,在实现机器人定位方面具有较好的特性.

1 UIF

采用UIF代替线性信息滤波器,UIF在扩展信息滤波体系结构中，嵌入了一种源于Sigma点滤波器的无迹变换方法,其非线性离散时间状态空间模型定义如下:

(1)

式中:xk为状态向量;zk为测量向量；wk，vk分别为过程噪声和零均值高斯序列的测量噪声,相应的协方差矩阵分别为Qk和Rk.

利用当前估计状态(xk|k)和协方差(Pk|k)计算一系列Sigma点,以预测下一帧的状态和协方差，即

(2)

式中:χ，W分别为2n+1个Sigma点和权重,通过缩放参数κ计算.

对Sigma点的状态进行传播,利用无迹变换计算出下一时刻状态和协方差为

(3)

(4)

(5)

信息状态贡献ik+1和关联信息矩阵Ik+1计算公式为

(6)

(7)

如果多个传感器获得的测量结果是同步的,则状态将与所有测量的叠加向量同时更新.在这种情况下,信息贡献项在回波和测量矩阵方面具有组对角线结构.因此,多传感器估计和数据融合的更新方程被表示为局部信息贡献项的线性组合，即

(8)

式中:m为传感器数量.

状态估计和误差协方差估计值被计算为

(9)

2 UIF-IMM

将UIF方法和IMM相结合,提出UIF-IMM算法.主要思想是使用IMM每一动作模式的估计进行数据融合,而不是将IMM的估计简单结合在一起.此外,该算法共享每个动作模式的模型似然函数,以提高多传感器系统中动作模式检测的性能.关于UIF-IMM算法的结构如图1所示,主要分为交互、滤波和融合3部分.

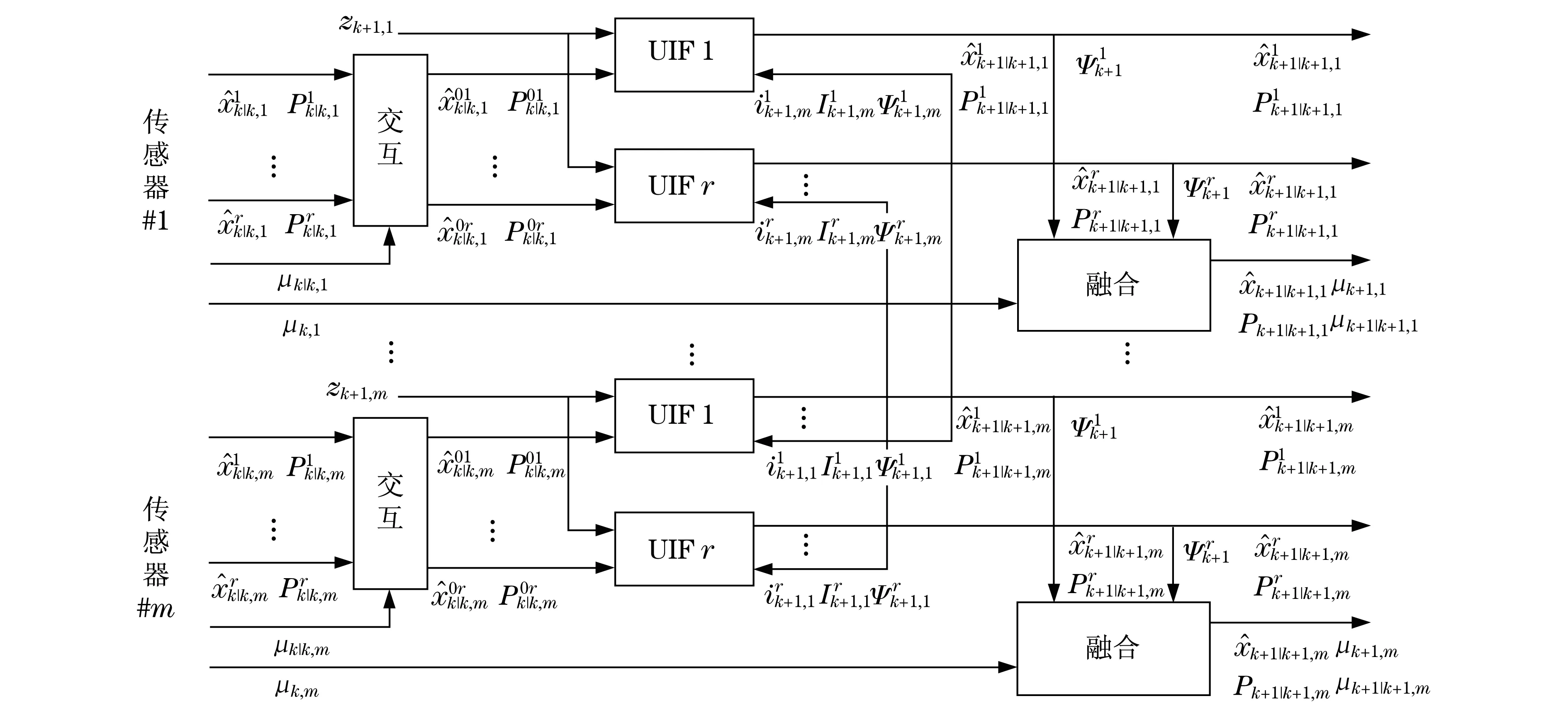
图1 UIF-IMM算法结构框图Fig.1 Block diagram of UIF-IMM algorithm structure

(10)

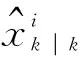
(11)

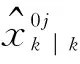
(12)

预测状态和误差协方差计算为

(13)

利用预测状态和误差协方差计算出信息状态向量和Fisher信息矩阵为

(14)

预测观测向量、回波协方差和交叉协方差分别被预测为

(15)

假设测量是同步得到的,则将IMM滤波器的每个动作模式的信息状态向量和信息矩阵更新为局部信息贡献项的线性组合，即

(16)

各传感器动作模式的状态估计和误差协方差为

(17)

对每个局部传感器节点的状态和状态协方差进行上述估计后,利用模型概率对状态和状态协方差进行组合,同时，利用IMM滤波器中的模型似然函数计算模型概率,IMM中每个动作模式的似然函数为

(18)

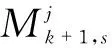
由于式(18)中的模型似然函数是通过局部测量和局部测量单元的估算计算的,因此，如果有多个传感器测量可用,可以通过融合其他局部模型似然函数来更新.每个动作模式的更新局部似然函数表示为累积似然函数，即

(19)

使用更新后的模型似然函数计算模型概率为

(20)

利用模型概率组合了每一种动作模式的状态估计和协方差估计，即

(21)

3 仿真结果

3.1 仿真条件

将UIF-IMM算法应用于机器人定位系统中.机器人移动速度为0.3 m/s,其运行轨迹如图1所示,轨迹规划目标如表1所示,采样时间为0.1 s.

图2 机器人运动轨迹Fig.2 Robot motion track表1 轨迹规划目标Tab.1 Trajectory planning target

阶段开始时间/s持续时间/s转角速率/(rad·s-1)10700.0270404.53110700.0418060-3.05240600.0

3.2 模型和参数

假定传感器站点的每个局部过滤器都使用由恒速(Constant Velocity,CV)模型和常数旋转(Constant Turn,CT)模型组成的IMM.

CV模型被定义为

(22)

式中:ξ，η为水平平面上的正交坐标;vk为零均值高斯白噪声的过程噪声,用于以标准偏差σv=3 mm/s2模拟加速度.

CT模型被定义为

(23)

式中:ω为转角速度;vk为具有零均值高斯白噪声的过程噪声,其标准偏差分别为σva=1.6 mm/s2σvω=0.2 rad·s-2.

3.3 仿真结果

从具有100次蒙特卡罗仿真实验中获得机器人跟踪估计误差.为了观测模型似然函数的影响,本文选择了两种UIF-IMM设计方案,UIF-IMM 1表示除式(20)外的IMM滤波器,而UIF-IMM 2则完全将UIM和IMM融合.为了验证该融合算法的有效性,本文对单传感器系统和集中式融合系统的跟踪结果进行了对比分析.机器人位置估计误差、角度跟踪误差分别如图3和图4所示,其统计结果如表2所示.

图3 位置跟踪误差Fig.3 Position tracking error

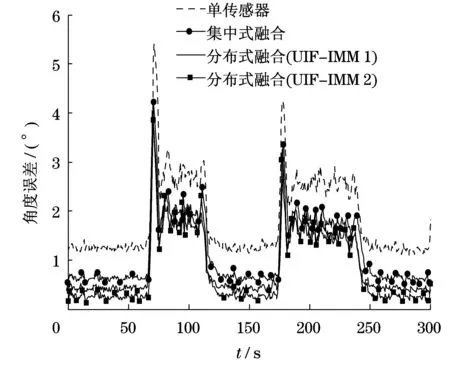
图4 角度跟踪误差Fig.4 Angle tracking error表2 估计误差Tab.2 Error of estimation

误差单传感器多传感器集中式UIF-IMM 1UIF-IMM 2RMS位置误差0.1580.0590.0680.047RMS角度误差2.11.21.20.9

分析图3和图4可知：采用多传感器对机器人跟踪具有更高的精度,因为其比单传感器跟踪系统可分析处理更多的测量结果,一定程度上避免噪声及外部干扰引起的误差.此外,在分布式传感器节点(UIF-IMM 2)中,采用模型似然函数组合的多传感器融合算法,其位置精度和角度精度均优于不进行组合的多传感器融合算法(UIF-IMM 1).在4种目标跟踪算法中,本文提出的算法定位误差最小,跟踪效果最好.

由表2可知：基于UIF-IMM 2的均方根位置误差和角度误差均最小,分别为0.047和0.9.而UIF-IMM 1的均方根误差与集中式融合系统的均方根误差几乎是重叠的,表明除了状态和状态协方差外,还应该采用模型似然函数的融合,以防止在分布式系统融合过程中的信息丢失.

进一步对模型概率估计结果进行了研究,以对比UIF-IMM 2与UIF-IMM 1两种方法,找出提高位置和角度精度的原因.如图5所示,UIF-IMM 2考虑了基于各种传感器的累积似然函数,使滤波器能够更精确地估计模型概率,从而对状态和协方差进行更精确的融合和估计.

图5 模型概率Fig.5 Model probability

4 结语

本文提出了一种新的机器人多传感器数据融合算法,该算法将UIF算法与IMM算法相结合,实现了分布式系统中的多传感器数据融合(UIF-IMM).为了提高动作模式检测和变化的性能以及跟踪精度,在UIF-IMM中提出了一种融合IMM滤波器模型似然函数的方法.对比不同算法下的机器人跟踪结果表明：本文提出的滤波方法可以很好地解决分布式多传感器环境下机器人的跟踪问题.