基于稀疏性非负矩阵分解的滚动轴承复合故障诊断

朱晓洁

(黄河科技学院 职业技术学院,郑州 450063)

当滚动轴承发生复合故障时,由于不同部位故障信号之间的相互干扰及耦合效应,复合故障信号表现得非常复杂,基于信号处理特征提取的滚动轴承复合故障难以取得好的效果.当前，大多采用智能诊断方法对滚动轴承复合故障类型进行分类[1-5].智能诊断中最关键的一步是特征提取,有效的故障输入特征不仅能提高分类正确率,而且还能提高计算效率.本文尝试将图像处理中的常用方法即非负矩阵分解方法用于滚动轴承复合故障的特征提取，进而实现滚动轴承的复合故障诊断.

1 非负矩阵分解

非负矩阵分解(No-negative Matrix Factorization,NMF)本义可追溯为一种矩阵分解和投影的多变量分析技术.用矩阵Vn×m表示待处理的m×n维多维样本数据,可对矩阵Vn×m进行分解,即

(1)

式中:Wn×r为基矩阵,也称为特征矩阵;Hr×m为系数矩阵.W,H均要求非负.

图1 非负矩阵图像处理示意图Fig.1 The sketch map of NMF

上述的非负性要求在图像处理中有着重要的实际意义,图1解释了NMF的基本思想:用Original表示原始特征图像,其可以表示为矩阵W和H的乘积,两个矩阵分别代表特征图像与系数矩阵.在NMF中要求特征矩阵与系数矩阵均为非负的:图像像素为负的物理现象在图像处理中是无法解释的,一系列标准的特征图像组成了特征矩阵中的各个列向量,其非负性就有效避免了上述无法解释物理意义现象的发生.此外,对于任意图像都具有一个公用的特征矩阵W,各个图像表现出的相异性体现在各自所对应的系数矩阵H上.据此,提取出图像的系数矩阵，并将其作为智能分类器的训练及测试特征向量，可有效提高智能诊断的效率和精确度.

2 稀疏性非负矩阵分解

稀疏性非负矩阵分解(Sparse No-negative Matrix Factorization，SNMF)是在NMF基础上与稀疏分解思想相结合而发展而来的一种NMF算法,它是在NMF基础上，对系数矩阵H添加稀疏性约束条件的算法.相对于NMF,SNMF算法具有如下优点:① 更稳定;② 更直观地反映原始数据的局部特征;③ 分解后的系数矩阵H具有更稀疏的数学表达,从而能用最少的特征维数来最有效地表示原始数据的特征;④ 求解收敛速度快.

下式求解的过程就是通过迭代更新,使V和WH的误差即‖V-WH‖最小化.可以用Frobenius范数作为目标函数来量化误差，即

(2)

并采用如下形式的交替乘法更新规则，进行迭代求解，即

(3)

从基于过完备字典的稀疏表示方式看,式(3)的目标函数可以写成如下的过完备字典学习的函数形式，即

(4)

s.t.W≥0, ∀i,Hi≥0,

C≜{W∈Rm×r

被称作矩阵凸集,其中矩阵W相当于稀疏分解中的过完备字典.在式(4)中W,Hi均要求非负性.从某种意义上来说,基于局部表达的NMF算法也是一种稀疏表示,只是这种表示的稀疏能力及程度相对较弱且还存在着控制难的缺点.通过对目标函数增添l1正则化的稀疏性约束条件,Hoyer等[6]提出SNMF方法,基于式(4)其目标函数为

(5)

由式(5)可知:当λ=0时,此式等价于NMF.相对于NMF,SNMF具有下述优点:不仅保留了NMF对局部特征稳定直观表达的优点,并且还能有效对分解后矩阵的稀疏度进行自由控制;SNMF处理后的系数矩阵与特征矩阵之间的相关性更小;SNMF增加的迭代次数不会对分解误差造成明显影响.

利用最小角回归(Least Angle Regression,LARS)算法在稀疏编码阶段对Ht进行求解，得

(6)

在矩阵更新阶段,通过极小化凸集上的目标函数来求Wt,得

(7)

采用块坐标下降法由Wt-1来求Wt,这样可将式(7)转化为

(8)

式中：A和B分别为稀疏矩阵、稀疏稀疏的权重因子.

3 所述方法流程

基于双谱时频图SNMF的滚动轴承故障诊断流程图如图2所示,大致分为如下步骤:

图2 基于双谱时频图SNMF的滚动轴承故障 诊断流程图 Fig.2 The bearing’ compound fault diagnosis process based on time-frequency SNMF

步骤1分别采集滚动轴承3种运行状态(内圈外圈复合故障、外圈滚动体复合故障及内圈外圈滚动体复合故障)下的振动信号,对每种运行状态下的数据进行分段,并分别对每段数据进行双谱变换.

步骤2分别随机选择3种运行状态下部分双谱时频图组成训练样本集XTrain(i)(i=1,2,3)(i代表滚动轴承的3种运行状态),对训练样本集XTrain(i)(i=1,2,3)的子集Vi(i=1,2,3)分别进行SNMF,得到3种运行状态下的标准图像集Wi(i=1,2,3).

步骤3将所有训练样本集XTrain(i)(i=1,2,3)分别向各自所对应标准样本集Wi(i=1,2,3)进行投影,得到每一副图像对应的系数向量,这些向量共同形成降维后的样本集HTrain(i)(i=1,2,3).

步骤4分别用HTrain(i)(i=1,2,3)训练支持向量数据描述(Support Vector Data Description,SVDD)轴承3种运行状态下的诊断模型.

步骤5同样,对测试样本集HTrain(i)(i=1,2,3)分别向标准图像集Wi(i=1,2,3)进行投影,得到每一副图像对应的向量系数,这些向量共同形成降维后的测试集HTest(i)(i=1,2,3).

步骤6将HTest(i)(i=1,2,3)分别输入到第4步训练后的诊断模型,从而对XTest(i)(i=1,2,3)所对应的轴承运行状态进行模式识别.

4 实验

以UN205滚动轴承为实验轴承进行相关实验,通过线切割的方式分别在轴承试件的外圈、内圈及滚动体上加工故障(零部件上的所加工的故障如图3所示),然后再组合滚动轴承的3种复合故障.

图3 试件各部位故障Fig.3 The fault location of the test bearing

3种复合故障的时域波形图分别如图4(a)～图4(c)所示.

分别对3种故障状态下的数据进行分段处理:每种状态下连续的512个采样数据作为一个样本,每组样本之间以重复1/2的数据方式依次向后连续截取.3种运行状态按上述数据样本截取方式分别取80组采样样本,其中每种状态下的前30组采样样本经过双谱时频分析后,将得到的双谱时频图进行SNMF分解,提取图像稀疏系数矩阵作为SVDD的训练样本训练3种SVDD模型:内圈外圈故障SVDD诊断模型、外圈滚动体故障SVDD诊断模型及内圈外圈滚动体故障SVDD诊断模型;同样每种运行状态下的后50组采样样本用同样方法特征提取后作为测试样本输入到上述训练好的SVDD模型中,进而进行分类.

图5(a)～图5(c)分别是轴承3种运行状态下某一采样样本的双谱时频图.图5中可以看出,虽然轴承在不同故障运行状态下双谱图存在很大差异,可以为后续SVDD诊断所需的特征提取提供很好的素材.但由于滚动轴承复合故障运行状态下，各个单个故障信号之间的相互干扰极有可能出现耦合现象,很难直接在其双谱时频图上提取有效的故障特征信息.

图4 滚动轴承3种复合故障的时域波形图Fig.4 The time-domain waveforms of the bearing’ three kinds of compound fault

以下对SNMF计算过程中的关键参数——特征维数、稀疏性因子λ以及迭代次数T的选取进行讨论.

(1) 特征维数的选择.首先选取迭代次数T=200,稀疏性因子λ=0.2,特征维数对分类精度的影响如图6所示.由图6可见,当特征维数选为4时,所述方法的分类精度比较低.其原因在于较小的特征维数选择不能全面有效表达原始特征图像中所蕴含的故障特征信息,造成部分故障特征信息的丢失,进而导致后续SVDD分类正确率的下降.当特征维数等于24时,所述方法取得了最高的分类正确率,说明了24维与实际的特征空间的维数相一致或相接近,正好蕴含了原始时频图中的所有故障信息.因此,取得了最高的SVDD分离结果.当特征维数大于24时,分类正确率虽然下降不多,但维数的增加会降低计算效率,而且还可能出现信息冗余及维数灾难等不好的结果.

图5 滚动轴承3种复合故障下的双谱时频图Fig.5 The bispectrums of the bearing’ three kinds of compound fault

图6 不同特征维数所对应的分类正确率Fig.6 The classification accuracy using different feature dimensions

(2) 稀疏性因子及迭代次数的选择.稀疏因子的作用是SNMF分解过程中控制稀疏矩阵的稀疏性,图7给出了不同稀疏因子所对应的目标函数误差(特征维数选为24,迭代次数为200).图7中可以看出:当系数因子等于0时,SNMF等价于NMF,会产生较大的目标函数误差;当目标因子不等于0时,虽然在理论上越大的稀疏因子就对应着更稀疏的稀疏矩阵,即得到最精炼的故障特征信息;目标函数的误差也随着稀疏因子的增大而增大,说明随着稀疏因子的增加,原始时频图像中所蕴含的故障特征信息损失也随之增加.

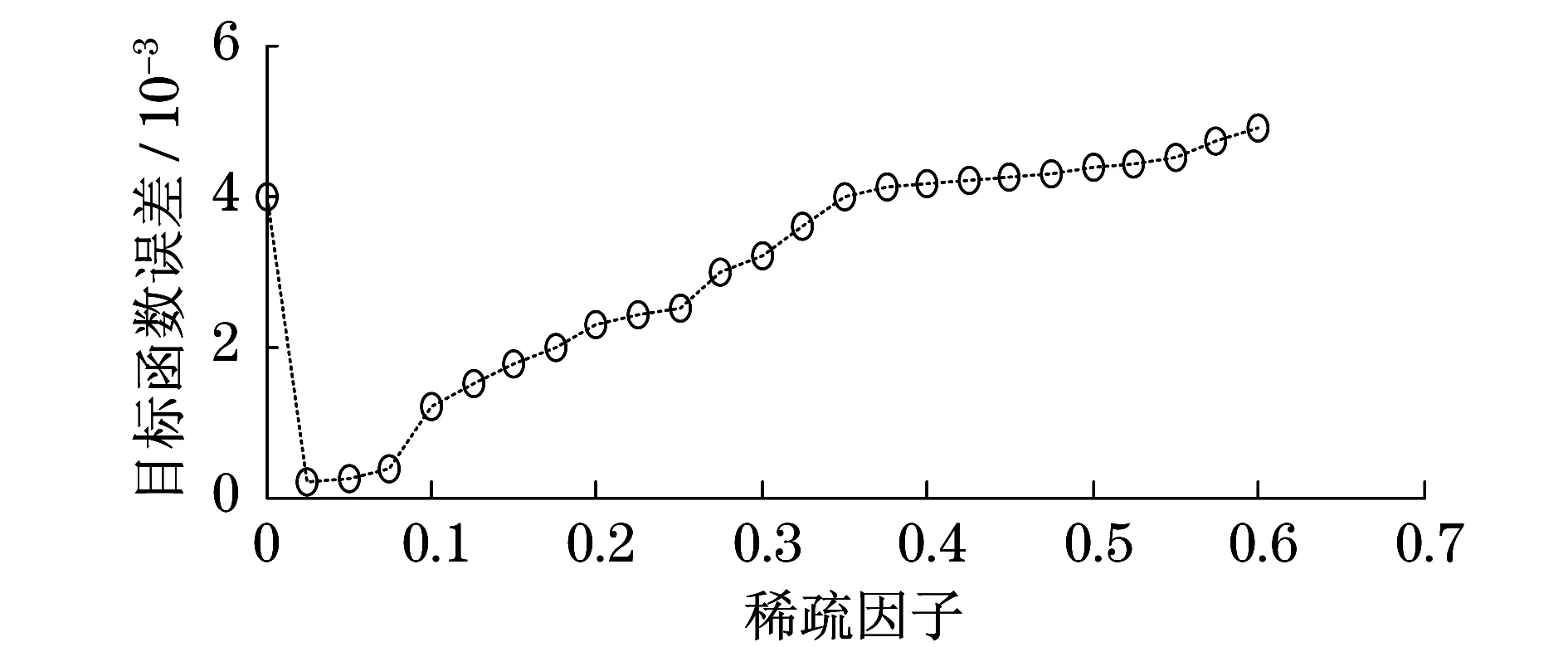
图7 稀疏因子对目标函数误差的影响Fig.7 The influence of sparse factor on objective function error

图8给出了不同稀疏因子所对应的分类正确率.太小或太大的稀疏因子都不能取得最理想的分类正确率;太小的稀疏因子造成矩阵稀疏系数的稀疏性不够,从而造成信息冗余或维数灾难;太大的稀疏因子会造成原始时频图像中故障特征信息的损失.从图8可以得出，稀疏因子选为0.2是最佳选择.

图8 不同稀疏因子所对应的分类正确率Fig.8 The different classification ratio using different sparse factors

迭代次数的选择没有具体的参考,按文献[6]选为200.

按图2所示的相关步骤进行特征选取后,首先用30组内圈外圈的训练故障特征信息进行SVDD诊断模型训练;然后将50组内圈外圈复合故障测试特征信息、50组外圈滚动体复合故障测试特征信息及50组内圈外圈滚动体复合故障测试特征信息共150组测试向量,输入到训练好的SVDD模型中,分类结果如图9(a)所示.其中1～50组对应的内圈外圈故障测试特征向量,51～100组对应外圈滚动体复合故障测试特征向量,101～150组对应内圈外圈滚动体复合故障测试特征向量.由分类结果可以看出:50组内圈外圈故障特征向量只有两组被误分,分类正确率达到了96%;而后两种故障(滚动体外圈复合故障、内圈外圈滚动体复合故障) 均被分类为非目标样本,正确率达到100%；总体分类正确率为98%,达到了理想的测试效果.同样,图9(b)和图9(c)是滚动轴承外圈滚动体、外圈内圈滚动体复合故障的分类结果,同样取得了好的分类效果.

图9 基于双谱时频图SNMF特征提取SVDD的诊断结果Fig.9 The fault diagnosis result based on bispectrum time-frequency SNMF feature extraction SVDD

5 结论

本文将基于图像处理的思想引入到滚动轴承的故障特征提取中来,提出基于SNMF-SVDD的滚动轴承复合故障诊断.首先对滚动轴承的3种复合故障信号进行双谱分析,得到3种运行状态下的双谱时频图像.对时频图像进行SNMF进行分解,得到双谱时频图像的稀疏系数矩阵作为SVDD的训练及测试特征向量.通过实验验证了所述方法具有较高的分类精度.此外,为突出SNMF在双谱时频图像特征提取中的优越性,对比了基于NMF-SVDD的分类结果.结果证明所述方法具有高的分类精度.