非奇异H-矩阵的几个判定条件*

李真好，余 敏，莫宏敏

(吉首大学数学与统计学院，湖南 吉首 416000)

非奇异H矩阵是一类特殊矩阵，在计算数学、经济数学和控制论等领域都有广泛的应用.如何给出非奇异H-矩阵的简捷的判定条件，一直是研究的热点[1-9].笔者拟改进文献[2]的主要结果，给出非奇异H矩阵的几个新的判定条件.

1 相关定义和引理

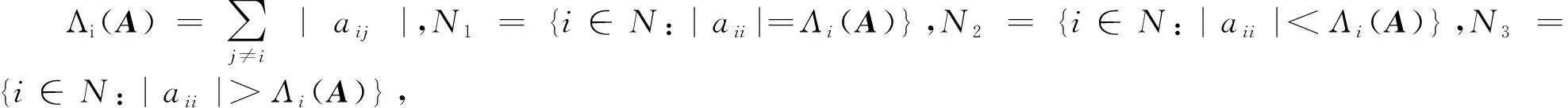
定义1[2]设不可约矩阵A=(aij)∈Cn×n，满足|aii|≥Λi(A),i∈N,且至少有1个严格不等式成立，则称A为不可约对角占优矩阵.

定义2[2]设A=(aij)∈Cn×n，满足|aii|≥Λi(A),i∈N,且至少有1个不等式严格成立，以及对每一个等式成立的下标i存在非零元素链aij1aj1j2…ajk-1jk,满足|ajkjk|>Λjk(A)，则称A为具有非零元素链的对角占优矩阵.

引理1[3]设A为不可约矩阵，X为正对角矩阵，若B=AX,则B也为不可约矩阵.

引理2[4]设A=(aij)∈Cn×n，若存在正对角矩阵X使得AX是非奇异H-矩阵，则A也是非奇异H-矩阵.

2 主要结果及其证明

设A=(aij)∈Cn×n，记

定理1设A=(aij)∈Cn×n，若

(1)

(2)

则A为非奇异H-矩阵.

证明由假设，对于∀i∈N1,有

(3)

对于∀i∈N2,有

(4)

(5)

构造正对角矩阵X=diag(d1,d2,…,dn),记B=AX=(bij),其中

因为ε≠+∞,所以di≠+∞.下面只需证明B∈D即可.

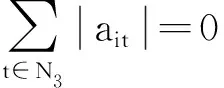
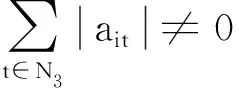
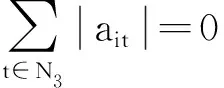
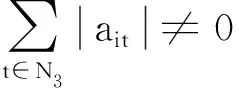
(ⅲ)∀i∈N3.由r的定义，有

则

综上所述，|bii|>Λi(B),i∈N+,即B∈D,故A是非奇异H-矩阵.

定理2设不可约矩阵A=(aij)∈Cn×n，若

(6)

(7)

且(6)和(7)式中至少有1个严格不等式成立，则A是非奇异H-矩阵.

证明构造正对角矩阵X=diag(d1,d2,…,dn),其中

设B=AX=(aij)∈Cn×n,则：

(ⅰ)对于∀i∈N1,有

(ⅱ)对于∀i∈N2,有

(ⅲ)对于∀i∈N3,由r的定义，有

于是，

即|bii|≥Λi(B).由引理1和引理2可知A为非奇异H-矩阵.

定理3设A=(aij)∈Cn×n，若(6)和(7)式中至少有1个严格不等式成立，且对每一个等式成立的i存在非零元素链aij1aj1j2…ajk-1jk,使得

或者，

则A是非奇异H-矩阵.

定理3的证明与定理2的类似，这里省略.

3 数值实例

由定理1可知，A满足定理的条件，故A为非奇异H-矩阵.又

由文献[2]中定理1可知，A不满足定理的条件，故无法判定A为非奇异H-矩阵.

由例1可知，定理1是文献[2]中的定理1的改进.