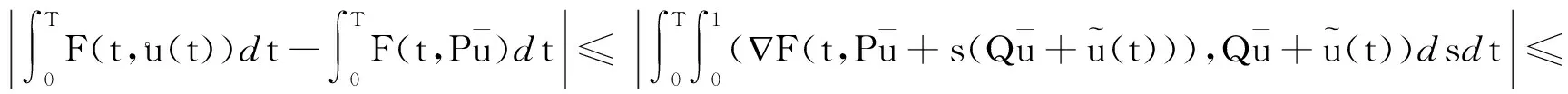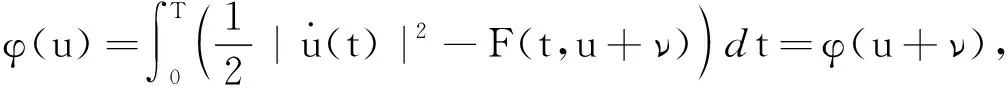一类二阶哈密顿系统的多重周期解*
孙 旸,张申贵
(西北民族大学数学与计算机科学学院,甘肃 兰州 730030)
考虑二阶哈密顿系统
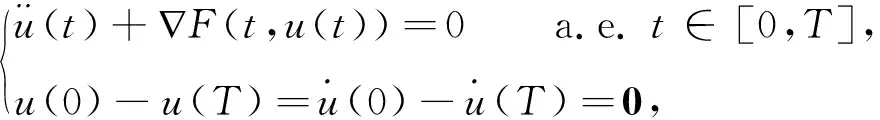
(1)
其中T为正常数.假设位势函数F:[0,T]×RN→R满足:
(H0)对于∀x∈RN,F(t,x)关于变量t可测;对于a.e.t∈[0,T],F(t,x)关于变量x连续可微,且存在函数a∈C(R+,R+)和b∈L1([0,T];R+),使得|F(t,x)|≤a(|x|)b(t),|F(t,x)|≤a(|x|)b(t).
{非线性哈密顿系统研究一直是数学和物理学中的热点课题,天体运动所对应的一些数学模型也可以转化为哈密顿系统的周期边值问题.1989年,J Mawhin等[1]讨论了二阶哈密顿系统的变分结构,并得到一系列可解性条件.随后,许多学者研究了二阶哈密顿系统周期解、次调和解和同宿轨的存在性.特别地,当具有线性增长非线性项,即存在函数f,g∈L1([0,T];R+),使得
|F(t,x)|≤f(t)|x|+g(t),
(2)
对于a.e.t∈[0,T]和∀x∈RN成立时,学者们[2-10]利用临界点理论探讨了二阶哈密顿系统周期解的存在性.笔者拟用一类控制函数w(|x|)替换(2)式中的|x|,从而推广文献[2-10]中的结果.
1 假设与主要结果
假设以下条件成立:
(H1)存在常数Mi(i=0,1,2)和非负函数ω∈C([0,+∞),[0,+∞)),满足:(ⅰ)ω(s)≤ω(t),∀s≤t,s,t∈[0,+∞);(ⅱ)ω(s+t)≤M0(ω(s)+ω(t)),∀s,t∈[0,+∞);(ⅲ)0≤ω(s)≤M1s+M2,∀s,t∈[0,+∞);(ⅴ)当s→+∞时,ω(s)→+∞.
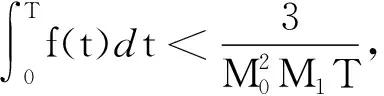
|F(t,x)|≤f(t)ω(|x|)+g(t),
(3)
对于a.e.t∈[0,T]和∀x∈RN成立.
(H3)
(4)
对于a.e.t∈[0,T]和x∈span{er+1,er+2,…,eN}成立,{ei}为RN中的标准基.
(H4)位势函数F(t,x)关于xi(1≤i≤r≤N)是Ti-周期的,即
(5)
对于a.e.t∈[0,T]和∀x∈RN成立,其中{ei}为RN中的标准基.

注1易知当控制函数ω(|x|)=|x|时,(H2)退化为线性增长条件,即(2)式.
(5)式中,当r=N时,称位势函数F(t,x)是周期的;当0≤r 其中β(t)∈L1([0,T];R+),则F(t,x)满足定理1的所有条件,但不满足文献[1-10]中定理的条件. (6) (7) 引理1[1]设X是巴纳赫空间,G是X上的离散子群.若泛函φ∈C1(X,R)有下界且G-不变,φ在X上满足(PS)G条件且r=dim(spanG)<+∞,则φ在X上至少有r+1个不同的临界点. 定理1的证明由条件(H1),对于s∈[0,1],有 (8) 由(6)—(8)式,有 (9) 从而,由(9)式可得 (10) 由(10)式,有 (11)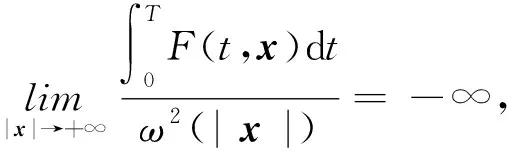
2 预备知识

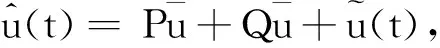

3 主要结果的证明