基于阻尼振动的轴承摩擦力矩测量方法

邢化友，孙瑞峰，田景志，张 涛，张 路

（1.西安轻工业钟表研究所有限公司，陕西 西安 710061；2.长安大学，陕西 西安710064）

轴承摩擦力矩是轴承领域用来衡量轴承特性的重要技术指标之一，轴承摩擦力矩的准确测定在许多工业和科学研究领域中都有重要意义。但是在测量轴承摩擦力矩时，必须了解各类测量设备的测量原理和适用范围。目前国内外在对轴承进行摩擦力矩测量时，多为径向加载测量且测量时轴承与测量装置之间有其他轴承摩擦外力介入，测量系统复杂且存在一定的测量误差。

本文所提出的轴承摩擦力矩测量方法是利用单摆原理径向加载的方式，通过能量守恒定律得到轴承摩擦力矩与摆角的关系，使用非接触式圆光栅测量系统，测量出摆锤第一次和最后一次摆至左侧或右侧时的最大摆角，可以得到该轴承的平均摩擦力矩，整个测量过程无外力介入且测量精度及效率都较高。

1 测试原理

基于能量守恒原理，如图1所示。在轴承内圈中穿过一固定圆轴，轴承外圈可在摆锤带动下自由地转动。在没有外力作用的情况下，根据能量守恒定律，摆锤每次摆动的最大角度相同。而摆锤在实际的往复摆动过程中，由于存在轴承的摩擦力矩和摆锤摆动产生的空气阻力，摆动的角度会逐渐变小，也就是说部分能量被消耗。因此，通过测量摆动角度的变化，可以计算出轴承的摩擦力矩和摆锤空气阻力共同作用下的能量损耗。另一方面，由于摆动速度很慢而且摆锤的迎风面很小。因此，在轴承摩擦力矩的测试过程中可以忽略空气阻力影响，通过测量摆动角度的变化，计算出轴承的平均摩擦力矩。

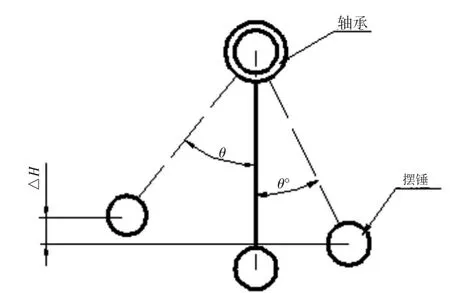
图1 测试示意图

假设摆锤质量为m，重力加速度为g，将摆锤摆放至与垂直位置夹角为θ的位置作为初始位置，使摆锤自由摆动至另一侧的最高位置θ′处。设初始位置和另一侧最高位置的高度差为△H.则根据能量守恒定律，轴承摩擦扭矩所耗能量W为：

在实际测试过程中，由于轴承的摩擦力矩很小，摆锤单次摆角的衰减量极其微小，通过传感器很难分辨两侧的摆角差值，因此在摆锤摆动多次后对多次累计的摆角衰减量进行测量。设质心与回转中心距离为l的摆锤由初始位置角度θ0自由释放，经过n个周期后传感器测出摆锤的摆角为θn.则根据式（1）得：

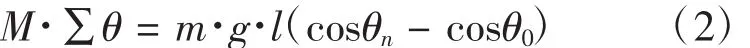
式中：M为轴承摩擦力矩；∑θ为摆锤摆动的角度和。

摆锤做往复运动的过程中，摆锤的摆动是一种欠阻尼的自由振动，检测的摆锤的摆动角度为振动幅值。可知任意两个相邻的幅值的比值为减幅系数是一定值，在摆锤连续的n次摆动中相邻摆角有以下关系：

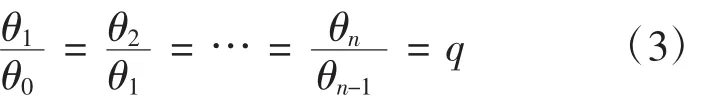
其比值为摆动的减幅系数q，在一个摆动周期后的摆角为初始摆角除以减幅系数，在阻尼振动中减幅系数为一指数量，其值如下：

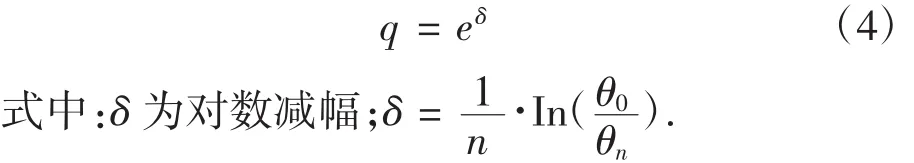
由式（3）和（4）可知摆角的初始值θ0和停止摆动角度θn之间有以下关系：

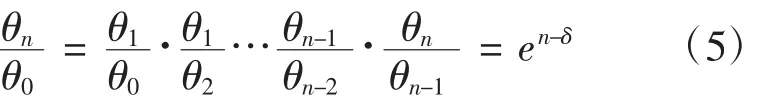
因此可以求出摆动过程中的减幅系数为：

由于过线轮摩擦力矩很小，两侧的摆动角度的差值十分微小，传感器无法分辨其差值，致使摆锤摆到另一侧位置时的角度无法测量，传感器检测的摆锤摆角始终为一侧的摆角，因此可取同侧两相邻幅值得均值作为另一侧的幅值，则在n个周期内，没有被传感器检测的一侧的摆角和为：

通过数列求和便可求出摆动的摆角和Σθ，根据式（3）可得轴承的摩擦力矩为：

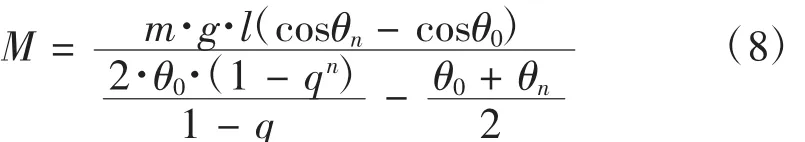
其中，M为轴承摩擦力矩，m为径向加载的重量，l为轴承回转中心到整个单摆质心的距离，q为一定周期内单摆摆动到左侧最大角度的减幅系数，n为第n个周期，g为重力加速度。

通过使用MathCAD软件对式（8）进行分析，得出影响误差的关键因素除传感器的精度外，初始摆角对测量误差同样存在较大影响，经过分析，在其他条件一定的情况下，随着初始角度的增大，测试的原理误差会随之降低，因此为保证有较高的测试精度，摆角的初始值不能选取的过小，可以在确定其余参数后，通过计算选取合适的初始角度保证测试精度。本文根据测试传感器及其余设备的精度，选取初始角度为10°，测试原理精度误差为0.02.

2 测试装置及结果

试验装置由圆光栅传感器[1]系统，数据采集系统及上位机数据处理组成，如图2所示：

a）圆光栅传感器系统由7200线码盘、读数头及细分盒等组成；

b）数据采集系统主要由以STM32F407IGT6为核心的采集卡组成；

c）上位机数据处理由Visual C++2017开发以适应Windows测试平台。

图2 测试装置组成及示意图

选取同一个轴承测量10次，分别径向加载10 kg、20 kg的条件下使用专用测量装置对轴承摩擦力矩进行测量。

周期内左右摆角的减幅很小。由于摆锤在摆动的过程中，在极限位置对测试装置产生轻微振动，圆光栅系统的测头和码盘发生相对位移，使传感器角度采集产生微小的偏差，造成实时曲线在左右两侧极限位置出现波动。见图3、图4.

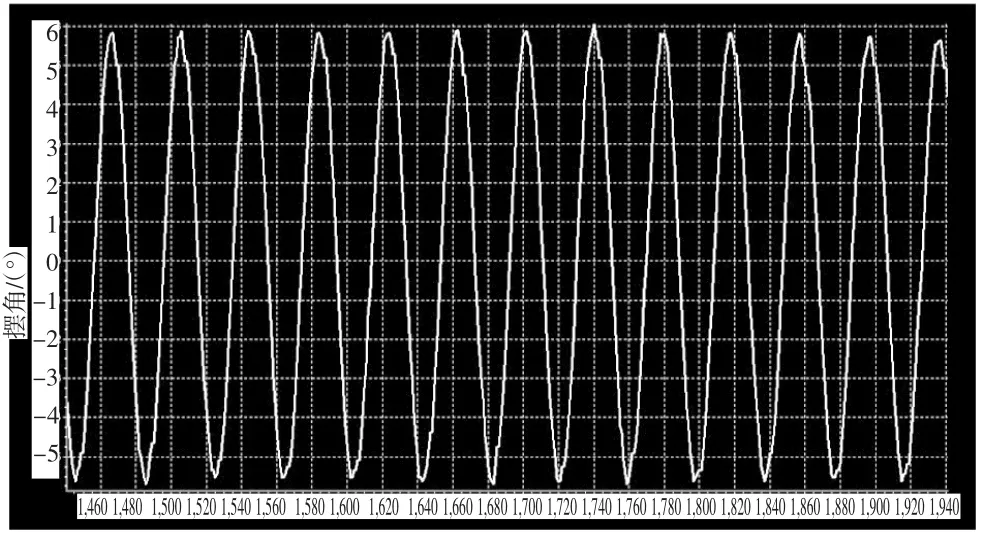
图3 径向负载10 kg下摆角实时曲线

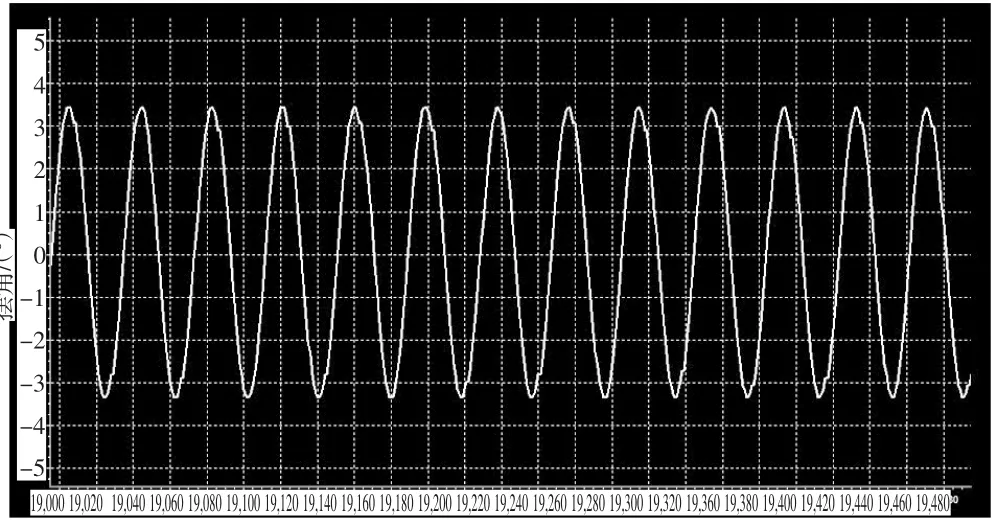
图4 轴承摩擦力矩试验平台

测试数据见表1、表2所示，从表中数据可以看出测试结果与计算得出的结果基本吻合，测试数据中存在的误差是由测试的原理误差和测试装置的加工制造误差组成，由于每个轴承加工的精度存在差异，同一个批次的轴承的摩擦力矩之间同样存在差异，但是整体的相对误差很小，同一批次的轴承的摩擦力矩不存在较大波动。由对比结果可以看出，本文给出的轴承摩擦力矩计算方法和为测试轴承摩擦力矩设计的专用测量装置稳定可靠。

表1 10 kg负载下测试数据

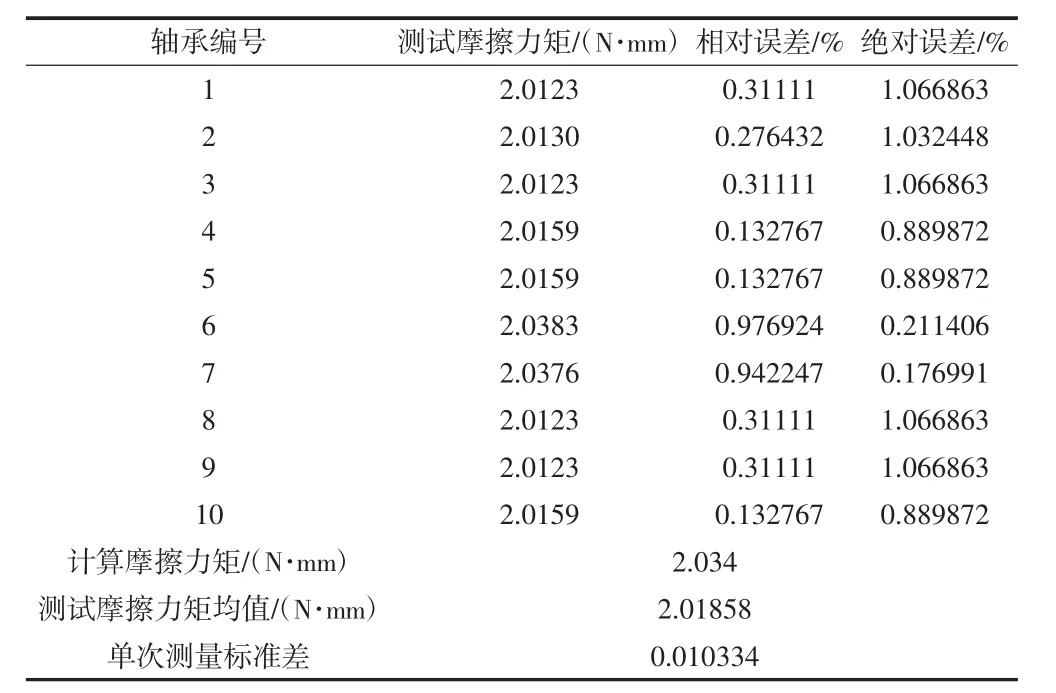
表2 20 kg负载下测试数据

3 结束语

本文对轴承的运动情况进行分析，给出了基于阻尼振动的轴承摩擦力矩测量运动方程，最终推导出摩擦力矩与摆角的关系并研制出了高精度摩擦力矩及摩擦系数测量设备。通过分析该测试方法及装置的误差，最终通过试验验证，对试验数据进行分析，分析结果表明在对同一个批次的轴承分别施加10 kg、20 kg径向负载进行摩擦力矩测试时，相对误差[2]在 0.15%～0.97%，绝对误差[2]在 0.17%～4.26%，通过测试结果可以看出该测量方法稳定可靠。

本文建立了用于进行轴承摩擦力矩测量的数学模型、测量方法及试验，不仅测量方法思想独特，而且所创建的结果新颖。通过实践证明，此测量原理、测试方法在工程上的适用性和可信性强，能够为轴承领域中对轴承摩擦力矩参数的测量提供有效的参考。