基于CATIA二次开发的直升机燃油重心计算及应用

蒋 辉，赵 辉，王 庆

（中国直升机设计研究所，江西 景德镇333001）

直升机的重心位置直接影响着飞行性能和操纵使用安全，直升机的重心包线是直升机在飞行使用中不可逾越的一道安全线，如果装载不当会造成重心位置超出重心包线范围，可能会造成机毁人亡的惨剧[1-3]，而直升机各部件、系统、设备、乘员、旅客、货物、武器、燃/滑油的重量重心位置，都将影响到直升机全机的重心，因此，在总体布置和安排时，应全面考虑和综合安排，使得直升机在各种使用任务状态下，其重心不得超出重心包线的范围[4]。

作为直升机基本系统之一的燃油系统，其燃油的消耗以及在载油不满的油箱中燃油所处姿态和位置（由于飞机姿态和加速度），都对直升机重心有较大影响[5]。由于燃油重心大幅变化所带来的飞行不稳定，一方面，将增加飞行操纵的负担，另一方面也将降低直升机的飞行品质，影响飞行任务的执行。因此，正确计算燃油重心的变化是确定飞机重心变化的重要依据[6]。

目前在燃油重心的计算方法上，已有不少的研究机构和学者提出了多种研究方法，包括切片法[7-9]、SPH 法[10-11]、ALE 法[12]以及 VOF 法[13]等等。基于切片法的燃油重心计算，可以较快地获得飞行器在稳态飞行过程中的燃油重心，是飞行器型号工程设计过程中比较常用的一种方法。而基于SPH法、ALE法以及VOF方法的燃油重心计算，则主要是利用有限元的方法来进行仿真计算，这三种方法可以在考虑油面晃动的情况下，对燃油重心进行短时瞬态的分析，分析精确较高，但其仅适用于时间历程较短的仿真计算，在做长时间历程（比如基于飞行剖面时间历程）进行分析时，计算量较大，计算耗时较长。

在直升机型号设计过程中，往往是根据不同飞行任务，以特定的燃油量来计算全机的重心，很少考虑因直升机飞行状态的不同，而导致的燃油重心变化，进而带来对全机重心的影响。本文将基于直升机的飞行剖面数据，考虑燃油液面的变化，对CATIA Automation API宏进行二次开发，采用切片计算与寻优分析相结合的方式，对某型直升机的燃油重心进行自动计算，并对燃油重心在全机重心评估中的应用进行简要介绍。

1 基于CATIA Automation API宏二次开发的燃油重心计算

CATIA的Automation API（自动化应用接口）提供了交互的方式，可通过录制宏（自动生成VBScript等）或Visual Basic平台等方式实现用户所需功能。该应用接口的模型设计功能比较全面，并具备了与任何OLE（对象连接与嵌入技术）所兼容的平台进行通信能力[14]。

1.1 燃油体及油平面

为便于燃油重心的计算，需要将油箱的燃油存储空间封闭为一个几何实体，即燃油体。以某型直升机为例，其燃油体如图1所示。

图1 燃油体模型

不同燃油量下的燃油体重心计算，应当首先确定出燃油的液面状态。虽然在直升机的飞行过程中，油箱内的燃油处于时时晃动的状态，燃油液面呈现出不规则的复杂曲面形状，但是对处于稳态飞行姿态下的燃油油面，工程上常常忽略燃油液面的复杂波动而把油面简化成平面来看待，即油平面，并经验证，这种简化能够满足解决工程问题的需要[9，15]。

根据相关文献[7，16]所述，油平面方程可表示为：

式中：A、B和C不同时为零，D为常数项。

由于油平面的法向向量N=（A，B，C）与过载向量n=（nx，ny，nz）的方向相同，其中nx、ny和nz分别为机体坐标系下X、Y、Z三个方向的过载分量[5]。因此，可以通过在CATIA中构建垂直于过载向量n=（nx，ny，nz）的切割平面来切割燃油体。油平面如图2所示。

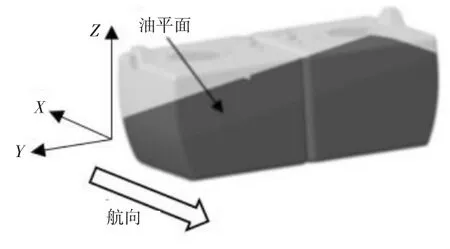
图2 油平面

1.2 基于Automation API宏的燃油重心计算

基于Automation API宏的燃油重心计算，可按图3所示流程进行。

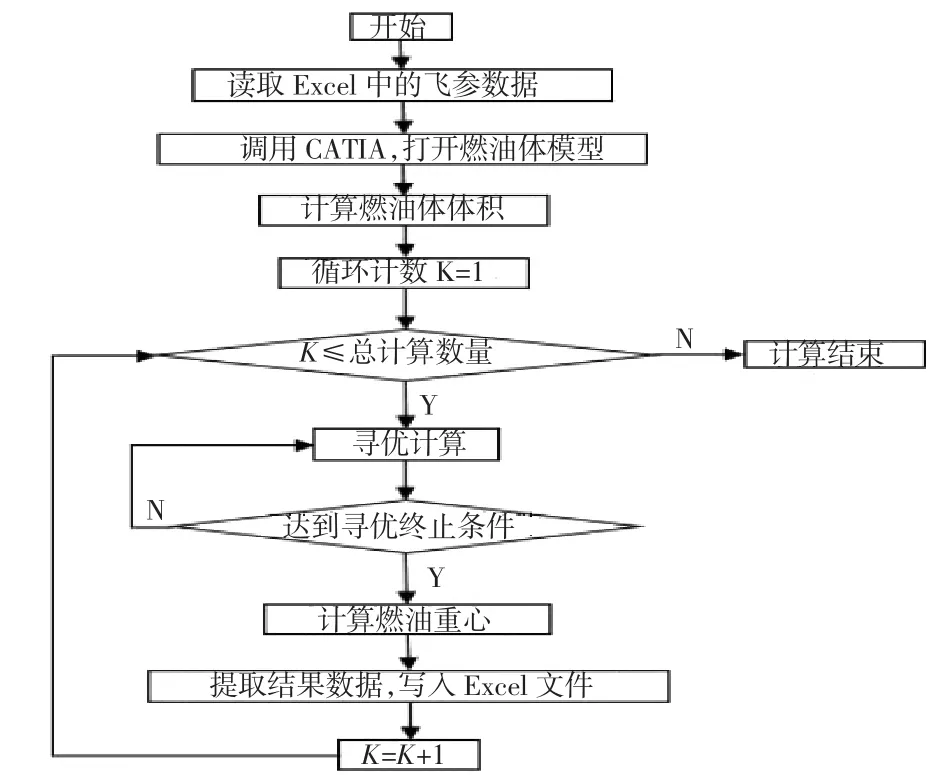
图3 燃油重心计算流程

1.2.1 飞行剖面数据读取

飞行剖面是指为完成某一特定飞行任务而绘制的飞机航迹图形，它由若干飞行状态组成，对于直升机而言，它包括滑行、起飞、垂直爬升、巡航、悬停、下滑、垂直着陆等飞行状态[17]。飞行剖面是飞行器战术技术要求的组成部分和重要设计依据，也是形象地表达飞行任务的一种形式[18]。飞行器的飞行剖面示意图如图4所示。

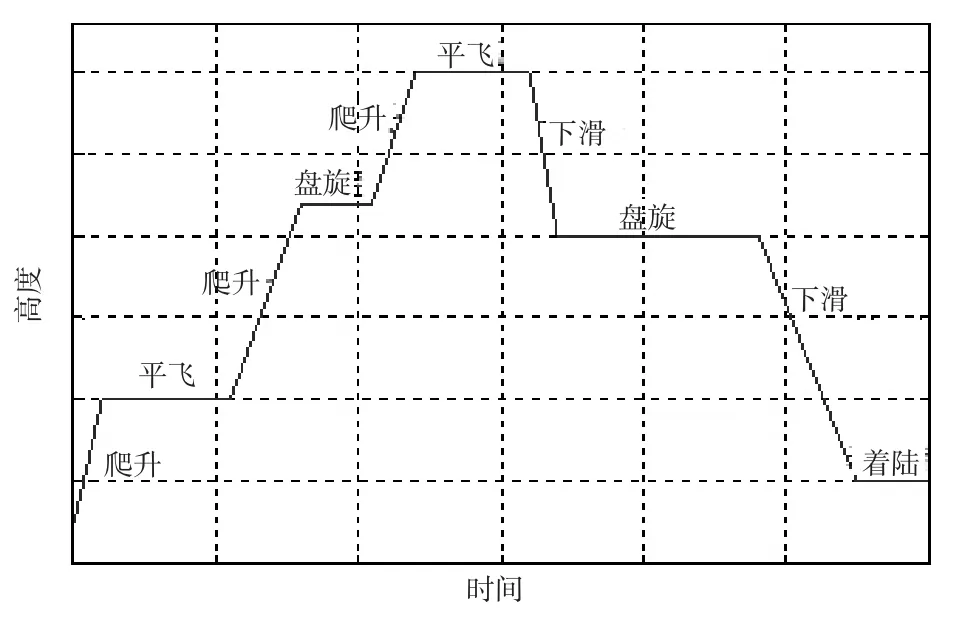
图4 飞行器的飞行剖面示意图

根据某型直升机的飞行剖面数据，计算出了该型直升机在不同飞行状态下三个方向的过载系数和剩余燃油量。表1中给出了部分飞行状态下的过载系数及剩余油量。

表1 过载系数及剩余油量

表1中的V为燃油箱中的剩余燃油量。

在进行燃油重心计算前，首先需要让CATIA能自动读取并存储包含有各飞行状态下过载系数及剩余燃油量的EXCEL数据，对应的CATIA宏流程如图5所示。

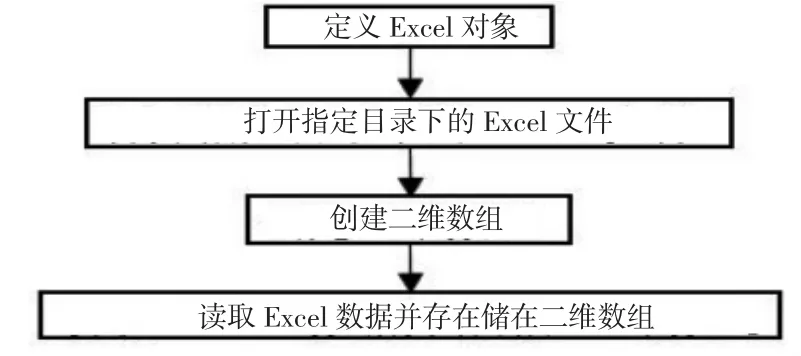
图5 飞行状态数据读取流程图

1.2.2 燃油体模型读取

在读取飞行状态数据后，需要由CATIA打开指定目录下的燃油体模型。

所要打开的燃油体模型中，除了有燃油体之外，还包括有以坐标原点和任意初始点（x0，y0，z0）所创建的直线段，以及垂直于该直线段且通过点（x0，y0，z0）的切割平面。在后续的计算中，点（x0，y0，z0）中的三个坐标值将由点（nx，ny，nz）所代替，则直线段可转变为过载向量的方向线，而切割平面也将平行于油平面。

1.2.3 燃油体的体积计算

为便于后续计算，需要提前定义燃油体的体积参数T，并计算当前燃油体的体积。对应的宏关键语句如式（2）和（3）所示：

//定义体积参数“T”

1.2.4 油量寻优计算

由于是要在给定的剩余燃油量的条件下，对燃油体进行切割，以便切割后的燃油量与表1中所给定的剩余燃油量相同，或者数值上极为接近。为此，需要采用寻优方法，以表1中的剩余燃油量V为寻优目标，以切割平面到原点的距离“L”为寻优变量，进行寻优计算，可建立寻优函数如式（4）所示。

式中，fL为寻优函数，T为每次切割计算后的燃油体体积。

当改变L值使得fL取得最小值时，即min（fL）值最接近于0时，可以认为T近似等于V，则寻优结束，并计算此时燃油体的重心。

在CATIA中，常见的可供使用的寻优方法有模拟退火算法（Simulated Annealing，SA）和共轭梯度算法（Gradient Algorithm）。其中模拟退火算法的思想最早是由N.Metropolis等人于1953年提出的[19]，该算法本质上属于蒙特卡洛方法，它的每次迭代必须进行多次目标函数计算，因而在处理实际问题时计算效率不高，且存在着最优解被忽略的可能性[20]。

共轭梯度算法最早是由Hestenes和Stiefle提出来的[21]，并由Fletcher和Reeves推广到求解非线性优化问题[22]，是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，不但克服了最速下降法收敛慢的缺点，还避免了牛顿法需要存储和计算Hessse矩阵并求逆的缺点，是求解大型线性和非线性方程组最有效的方法之一。

共轭梯度法的原理是在寻优过程中，利用当前点xk处的梯度向量g（xk）和前一迭代点xk-1处的搜索方向dk-1对最速下降方向进行如下修正：

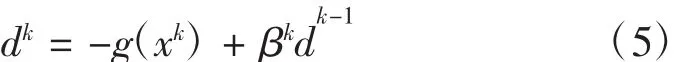
并保证新的搜索方向dk与之前的搜索方向dk-1，dk-2，...，d0之间满足共轭关系。而其中修正系数βk的不同又进一步形成了不同的共轭梯度法[23]。

在CATIA中采用共轭梯度算法进行寻优，需要分别设置寻优目的类别、寻优算法、寻优变量的上下限、寻优迭代终止的判据等四项关键参数。

对于寻优函数式（4），需要在每一个飞行状态点下寻找其最小值，因此，设置寻优目的类别为寻找最小值，即：

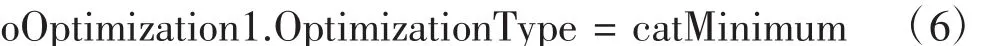
设置寻优算法为共轭梯度法：

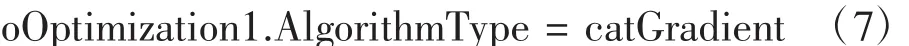
如前所述，需要设置切割平面到原点的距离L为寻优变量，考虑到该型直升机燃油箱模型的实际情况，可设置L的上下限分别为2000和0，即：

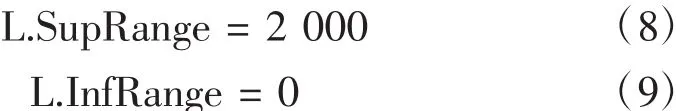
为保证在寻优精度已能满足实际需要的情况下，亦即fL值非常接近于0时，CATIA能够停止当前飞行状态下的寻优计算而进入到下一个飞行状态的寻优计算，可设置单次寻优的最大迭代次数为500次或者设置最长寻优时间为5分钟，即：

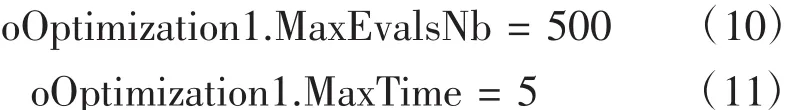
1.2.5 燃油重心计算

经寻优计算后，所得到的被切割后的燃油体体积可以认为等于飞行剖面数据中所给定的剩余燃油体积V，此时便可以通过（12）~（17）这6条关键语句来获得燃油体在X和Y方向上的重心。

//建立当前燃油体的参考“oRef”

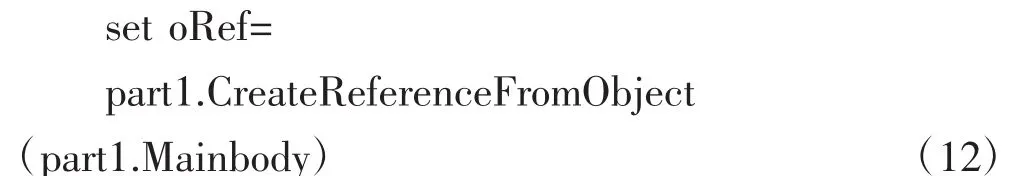
//获取当前工作台的空间分析模块“SPAWorkbench”

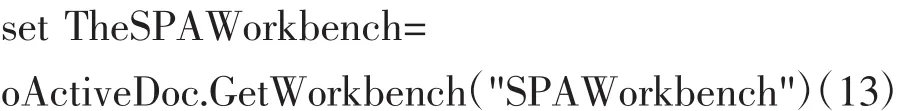
//获取参考“oRef”的可测量对象

//获取参考“oRef”可测量对象中的重心坐标

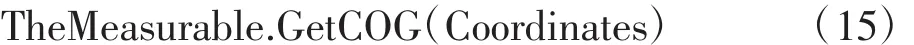
//将重心坐标的x和y值分别赋予Gx和Gy

其中Gx和Gy即为燃油体在X和Y方向上的重心。

由于飞行器在Z方向的重心变化往往较小，且对飞行器的性能影响不大，通常不作Z方向的重心计算。

1.2.6 计算结果输出与分析

通过前面对函数fL以及重心的计算，可得到各飞行状态下fL、X方向重心和Y方向重心变化曲线如图6~图8所示。

从图6中可以看出，通过寻优计算所得到的每一个飞行状态点下的fL值，即切割后的燃油量T与所给定的剩余燃油量V的差值均在10-5量级左右，已足够小，表明切割后的燃油量可以近似等于所给定的剩余燃油量，此时的燃油体可以用于对重心的计算。

图6 fL的变化曲线图

从图7中给出的X方向重心变化曲线图中可以得到，在整个飞行剖面中，直升机的燃油在X方向的重心变化范围为：9 807.219 mm~9 914.871 mm，变化幅度为107.653 mm.

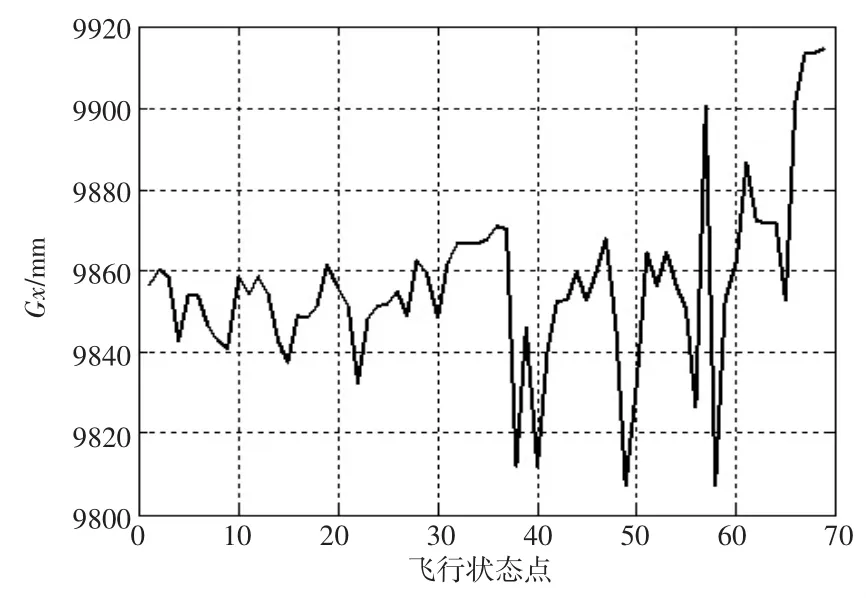
图7 X方向重心变化曲线

其中，X方向上的重心最小值Gx=9 807.219 mm，出现在第49个飞行状态点处，此时对应的飞行状态为水平加速。

X方向上的重心最大值Gx=9 914.871 mm，出现在第69个飞行状态点处，此时对应的飞行状态为垂直着陆。

从图8所给出的Y方向重心变化曲线图中可以得到，在整个飞行剖面中，直升机的燃油在Y方向上的重心点大致交替地位于机身左右两侧，且更大幅度地偏向于机身左侧，即-Y方向。整个Y方向上的重心变化范围为：-197.68 mm~58.545 mm，变化幅度为256.225 mm.

Y方向上的重心最小值Gy=-197.68 mm，出现在第69个飞行状态点处，此时对应的飞行状态为垂直着陆。

Y方向上的重心最大值Gy=58.545 mm，出现在第58个飞行状态点处，此时对应的飞行状态为水平减速。

此外，可以发现，该型直升机在整个飞行剖面中，Y方向上的重心变化范围约为X方向上的重心变化范围的2倍，即燃油在机身横向上的重心变化范围约为纵向重心变化范围的2倍，这不仅与整个飞行剖面中的飞行状态有关，也与燃油箱的横向尺度约为纵向尺度的2倍有关。

2 燃油重心在全机重心评估中的应用

如前所述，燃油重心应当满足全机重心的要求。根据直升机的飞行剖面，其各飞行状态下的全机重心坐标可以表示为[5]：

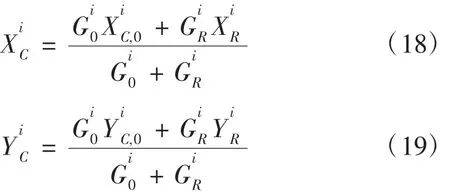
结合各飞行状态下的燃油重量，通过将图7和图8中的燃油重心数据带入式（18）和式（19），可以计算出各飞行状态下的全机重心坐标，并与全机重心包线图进行比较，当且仅当各飞行状态下的重心位置均位于全机重心包线内时（如图9和图10所示），才能满足直升机对重心的使用要求。

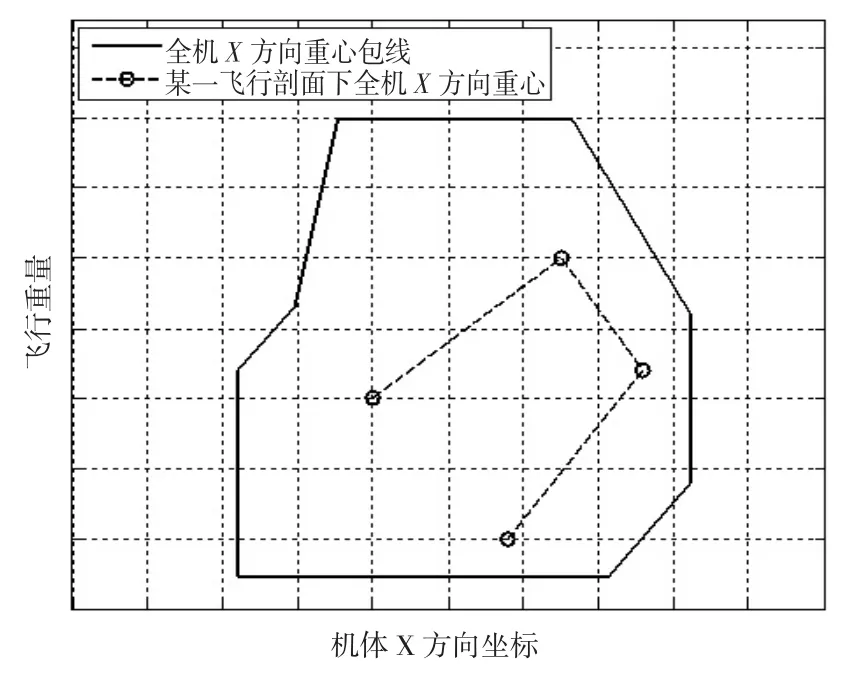
图9 X方向重心包线示意图

图10 Y方向重心包线示意图

如果所计算出的燃油重心使得全机的重心超出了重心包线范围，就至少需要从以下几个方面来考虑对燃油系统进行设计改进：

（1）更改燃油箱的几何外形，以改善燃油在燃油箱中的分布情况；

（2）对于大型燃油箱，可以通过在燃油箱内增加挡板或者将大燃油箱更改为若干个小燃油箱，减少因为燃油在燃油箱中大尺度范围内的晃动而导致重心的剧烈变化；

（3）重新调整燃油箱在直升机上的安装位置；

（4）增设转输系统和引射系统，对各燃油箱里的燃油量进行主动分配和调整；

（5）调整相邻燃油箱之间的高连通孔位置，或者在低连通孔处增设重力单向活门，通过控制燃油在各燃油箱中的蹿流方向，达到控制燃油重心的目的。

通过以上几个方面对燃油系统进行改进设计后，需要重新根据飞行剖面再次计算燃油重心以及全机重心，经多轮迭代，直至能够满足全机重心的要求。

3 总结

（1）以某型直升机燃油箱为研究基础，提出了基于飞行剖面数据，考虑不同过载系数下燃油液面的变化，来对燃油重心进行计算，并以此对全机重心进行评估的思路；

（2）对CATIA Automation API宏进行了二次开发，采用切片计算与寻优分析相结合的方式，对燃油重心进行了自动计算，得到了对应于该型直升机飞行剖面中各飞行状态下的燃油重心变化曲线图，并发现，在该飞行剖面下，燃油在机身横向上的重心变化范围约为纵向重心变化范围的2倍；

（3）给出并解释了基于CATIA Automation API宏二次开发的燃油体积计算、寻优设置以及重心计算的部分关键语句；

（4）对所获得的燃油重心在全机重心评估中的应用进行了介绍。