计及智能电表非同步性特性的配电系统状态估计
林小峰,谭晓虹,宋绍剑,方 治
(广西大学电气工程学院,广西 南宁530004)
状态估计在配电系统运行中起着至关重要的作用。配电系统状态估计为配电管理系统的应用(包括实时监控)提供初始状态/条件,其准确性和可靠性都会对电网的运行造成重要影响[1]。加权最小二乘法为基本算法,在传统配电系统状态估计中广泛应用[2]。但是,配电系统状态估计(DSSE)面临着缺乏足够的、准确的测量值问题[1]。截至2013年10月底,已累计安装应用智能电表1.73亿只[3],智能电表的推广,为配电系统状态估计提供大量冗余测量。但智能电表提供的信号通常不同步,智能电表的测量时间之间也有很大的不同。当智能电表测量一些电变量时,需要记录采样时间。
本文针对实际DSSE中,智能电表的测量异步问题,提出了一种有效的解决方案。改进方法与传统方法相比提高DSSE的精度,并能很好处理负荷突变情况。
1 非同步智能电表的配电系统状态估计
在本文中,设定智能电表的采样周期为15分钟。测量值在这个间隔期间没有更新,称为延时(OD)信号。该方法将短期负荷变量引起的误差分为两个部分:1)测量装置的误差;2)由短期负荷变量引起的误差。
第一个部分已经得到了很好的研究证明,其遵循零均值和特定标准差的高斯概率密度函数(probability density function,PDF)。第二个部分的误差(即从OD信号产生的)可建立为一个服从正态分布的随机变量模型。总误差的建模可以为两个正态分布的随机变量的组合,这也是一种正态变量[4],可纳入DSSE过程

其中 μtotali、μmi和 μODi分别为总平均值,测量设备误差的平均值和OD信号误差的平均值;σtotali、σmi和σODi分别为总标准差、测量设备误差的标准差和OD信号误差的标准差。误差的平均值和标准差可通过智能电表的历史数据得到。
通常情况下,可以假定平均值和标准差在两个连续采样事件之间的时间间隔内呈线性变化。对于一个OD信号,时间自上次更新是通过可变tLU表示。因此,DSSE计算过程中的平均值和标准差为

在改进方法中,总误差的平均值是根据式(1)和(3)计算,测量方差是通过式(2),(4)求得,并且更新相应R矩阵。
2 算例分析
在本节中,用IEEE 33配电测试系统验证改进方法的有效性。智能电表和传统电表的配置见图1,本文安装25个智能电表,安装2个潮流测量电表,即传统电表,测量支路潮流。

图1 IEEE 33母线系统中算例的电表配置
负载变化类似于图2的基于英属哥伦比亚大学记录历史数据的24 h相对于峰值的典型负荷曲线变化,算例研究为24 h内每分钟执行一次DSSE(一天内进行1440次)。为了模拟异步采样,对每个智能仪表分配一个0~15之间的随机整数。这个数字表示每个智能电表第一次采样的时间(min)。假设智能电表的精度为0.5%,传统电表精度为2%.

图224 h相对于峰值的典型负荷曲线
在第一种方法中,进行传统的DSSE,不考虑测量的异步性,而在第二种方法中,采用所提方法调整方差。在利用加权最小二乘法计算状态向量后,可以计算DSSE的误差。在本文中,对所有的母线电压定义DSSE的二范数误差为

随机噪声的影响:由于假设测量噪声是随机的,可以预期每次模拟运行时结果都会发生变化。用式(5)计算各种方法的DSSE误差,结果如图3所示。为了证明这些误差为积累测量,也是集成的DSSE误差,结果如图3(b)所示。如图3中,在一天中改进DSSE方法结果的总累计误差为7.543 9,相比与传统DSSE方法(9.548 3)有明显减少。改进方法对测量值的均值和方差设置不同,从而达到更高的精度。

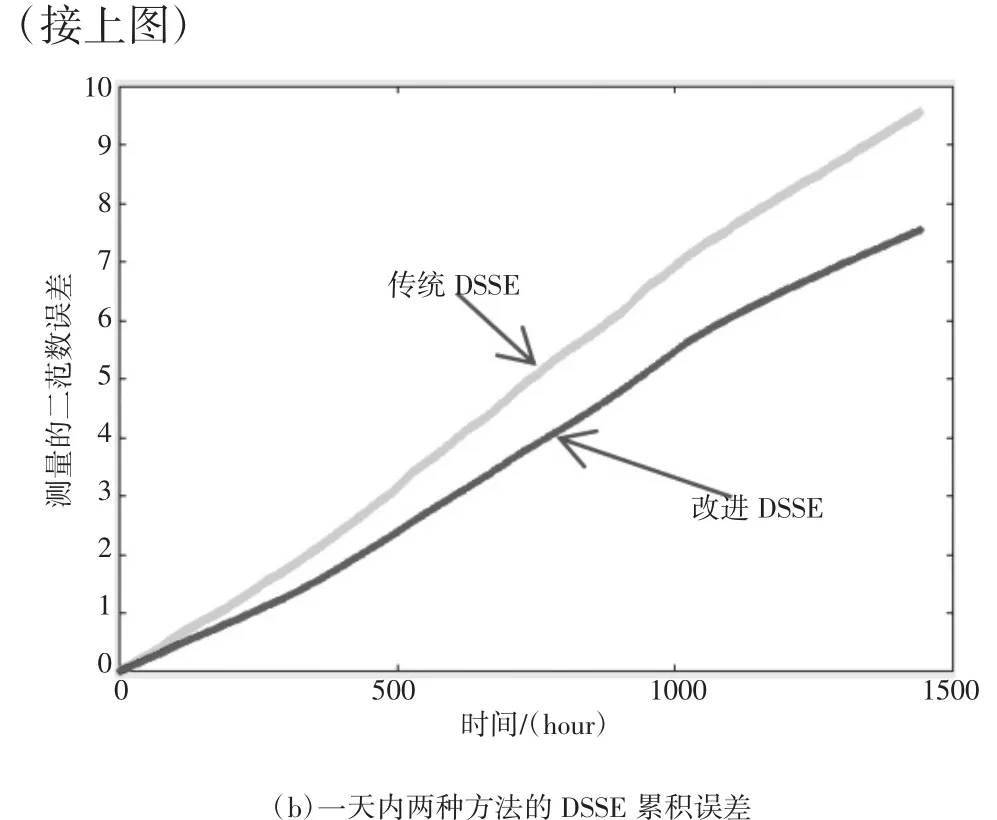
图3 两种方法的精度比较
3 结束语
本文研究配电系统中,针对智能电表非同步特性问题,提出DSSE改进算法。设定在短时间内变化服从正态分布,应用所提算法,根据OD调整每个智能电表测量误差的方差和平均值。相对于传统DSSE,该方法考虑了测量的非同步性。在IEEE 33测试系统中,本文验证了该算法的有效性。仿真结果表明,改进方法明显优于传统方法,改善了DSSE的精度。

