2018全国高中数学联赛安徽省初赛第七题的多种解法与推广
2018-12-22 03:26
中学数学教学 2018年6期
安徽省宿州市砀山中学 (邮编:235300)
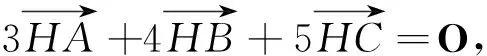
1 解法探究
解法1 (几何法)

图1
由奔驰定理得,S△BHC∶S△AHC∶S△AHB=3∶4∶5,
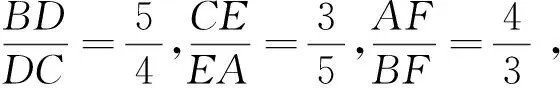
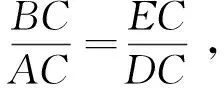
在直角Rt△ADC中,
又因为∠ACB+∠AHB=π,
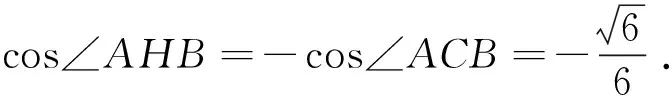
解法2 (向量法)

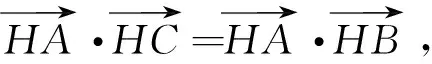
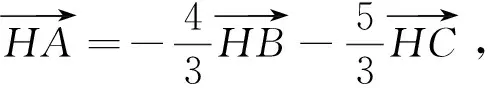

所以
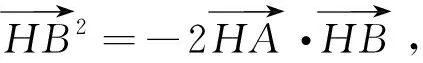
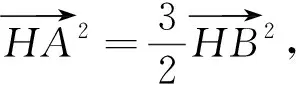
解法3 (坐标法)
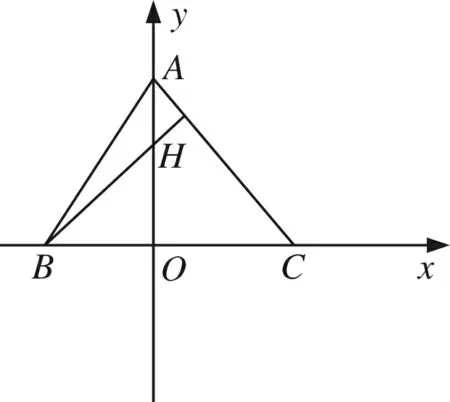
图2
建立如图所示的平面直角坐标系,令A(0,a),B(b,0),C(c,0),H(0,h),

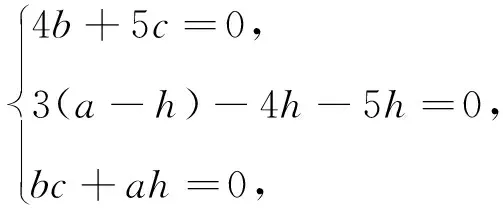
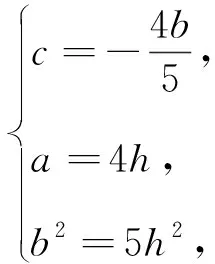
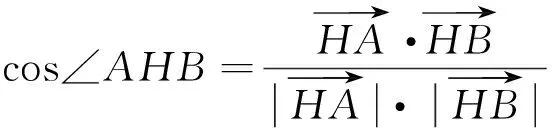
解法4 (垂心性质)
因为H是△ABC的垂心,所以tanA∶tanB∶tanC=3∶4∶5,
令tanA=3k,tanB=4k,tanC=5k,
又因为tanA+tanB+tanC=tanA·tanB·tanC,

又因为 ∠ACB+∠AHB=π,

2 结论推广

图3
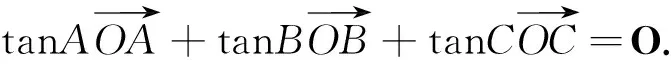
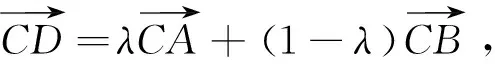

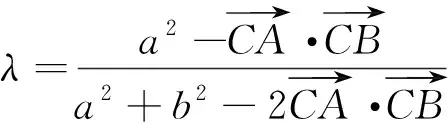
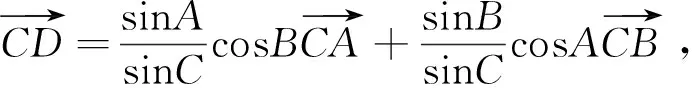

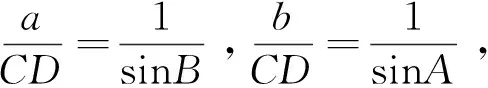



结论2 在△ABC中,角A、B、C所对的边为a、b、c,若O为△ABC的重心,则有x=y=z;
结论三在△ABC中,角A、B、C所对的边为a、b、c,若O为△ABC的外心,则有sin2A∶sin2B∶sin2C=x∶y∶z;
结论四在△ABC中,角A、B、C所对的边为a、b、c,若O为△ABC的内心,则有a∶b∶c=x∶y∶z;
结论五S△BOC∶S△AOC∶S△AOB=|x|∶|y|∶|z|.
3 应用举例
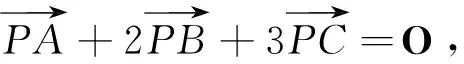

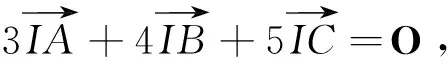
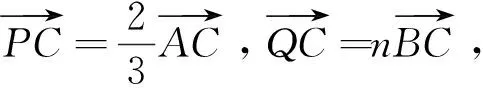
猜你喜欢
今日农业(2022年1期)2022-11-16
长江蔬菜(2022年15期)2022-08-06
学校教育研究(2022年7期)2022-04-24
中学生数理化·高一版(2022年2期)2022-04-05
今日农业(2021年12期)2021-10-14
中等数学(2021年6期)2021-08-14
今日农业(2021年5期)2021-05-22
中学数学研究(江西)(2018年11期)2018-12-04
宝藏(2018年10期)2018-10-18
宝藏(2018年10期)2018-10-18

