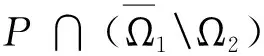一类非线性分数阶微分方程无穷积分边值问题的正解

李耀红，张海燕

宿州学院数学与统计学院,宿州，234000

本文考虑一类分数阶无穷积分边值问题(FBVP)：

(1)

1 预备知识

为了后文叙述方便，给出如下假设：

(H1)f∈C([0,+)×[0,+),[0,+))，在[0,+)×[0,+)上不恒等于0，且在[0,+)上当u有界时f(t,(1+tα-1)u)有界；

(H2)g∈C([0,+),[0,+))，在[0,+)上不恒等于0，且g(t)(1+tα-1)dt<+；

(H3)h(t)∈L[0,+),t∈[0,+)，且Δ1=h(t)tα-1dt<Γ(α)，Δ2=h(t)dt<+。

为简洁，本文略去一些常用的分数阶微分计算的标准定义和定理，其在分数阶相关研究文献中均可阅览，详细内容也可参阅文献[4]。为方便读者，下面给出一些必要的引理作为预备知识。

引理1.1[1]若函数y∈C[0,+)，则方程

(2)

有唯一解

这里G(t,s)=G1(t,s)+G2(t,s),且

(3)

引理1.2[1，5]当k>1时，G(t,s)满足

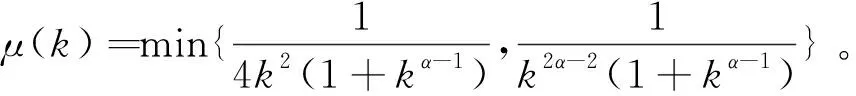
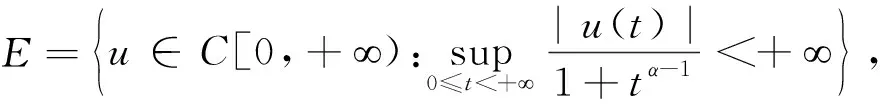
(4)

定义算子A:P→E

引理1.3若(H1)-(H3)成立，则A:P→P是全连续的。

证明首先对∀u∈P，有

=μ(k)||Au||

(5)

因此，可知算子A:P→P。接着利用与文[1]相同方法，可证算子A在锥P的有界集内一致有界，等度连续，同时由勒贝格控制收敛定理和函数f的连续性知，算子A是连续的。综上所述可知：A:P→P是全连续的。

(i) ‖Au‖≤‖u‖,u∈P∩∂Ω1；

‖Au‖≥‖u‖,u∈P∩∂Ω2；

(ii) ‖Au‖≥‖u‖,u∈P∩∂Ω1；

‖Au‖≤‖u‖,u∈P∩∂Ω2，

2 主要结果

为了方便，引入如下记号：

定理2.1若(H1)-(H3)成立，且f=0，f0=+,则FBVP(1)在P中至少有一个正解.

证明由引理1.1知A:P→P是全连续的，因此只需证明算子A在P中至少有一个不动点即可。由f=0，则存在充分大的μ1>0以及一个任意小的ε1>0，使得

f(t,u)≤(f+ε1)u,∀t∈[0,+),u≥μ1

(6)

其中Δ(f+ε1)g(s)(1+sα-1)ds≤1。令Ω1={u∈P,‖u‖<μ1},对∀u∈∂Ω1∩P,利用(3)式和(6)式，可知：

≤Δ(f+ε1)g(s)uds

≤Δ(f

≤Δ(f+ε1)g(s)(1+sα-1)ds‖u‖

≤‖u‖

即

‖Tu‖≤‖u‖，∀u∈∂Ω1∩P

(7)

另一方面，由f0=+，则存在0<μ2<μ1以及一个任意小的ε2>0，使得

f(t,u)≥(f0-ε2)u,∀t∈[0,+),0

(8)

‖Tu‖≥‖u‖,∀u∈∂Ω2∩P

(9)

定理2.2若(H1)-(H3)成立，且f0=0，f=+,则FBVP(1)在P中至少有一个正解。

证明证明方法与定理2.1类似,此处省略。

例2.1一类分数阶无穷积分边值问题(FBVP)