基于模糊PID控制器的变质量-柔性梁结构振动主动控制
马驰骋, 罗亚军, 张希农, 程相孟, 邵明玉
(1.山东理工大学 交通与车辆工程学院,山东 淄博 255000;2.西安交通大学 机械结构强度与振动国家重点实验室,西安 710049)
随着科技的发展,越来越多的人力劳动被机械所替代,在各个工业领域,机械自动化程度越来越高,人们设计出多种多样的机械臂以满足不同的工业需求。由于柔性臂结构具有细长和质量轻等特点,振动频率低,若不采取有效的措施对其振动进行抑制,将严重影响柔性臂结构的操作精度和安全性[1-3]。杜欣等[4]针对末端附带集中质量的双连杆柔性机械臂,采用LQR方法设计作动器控制律,有效地抑制了柔性臂的弹性振动,提高了柔性臂的运动精度。刘旭亮等[5]以三旋转关节刚柔耦合机械臂为研究对象,分析了仿人手柔性臂末端负载引起的残余振动,为机械臂的精确化振动控制提供了参考。为抑制空间机械臂系统在转动过程中激起的柔性臂的弹性振动,娄军强等[6]提出了基于Lyapunov稳定性的模糊自适应速度反馈控制策略,利用压电致动器有效的抑制了柔性臂的弯曲振动和扭转振动,提高了柔性机械臂系统的末端定位精度。
另一方面机械臂结构通常用来传递或者搬运物品,而物品的位置移动或者质量改变都会引起系统质量参数的改变,使得这类结构属于典型的变质量结构。系统质量参数的变化给结构的动力学特性带来显著影响,增加了控制的困难性和复杂性。为解决移动质量作用下的弹性梁结构的振动问题,Nikkhoo等[7]设计了含时变增益矩阵的线性优化控制算法有效的控制了结构的多阶模态。吴忻生等[8]则通过边界控制策略,成功地抑制了末端具有未知扰动的柔性机械臂的振动,该控制策略可达到外界干扰下的指数稳定。李发宗等[9]将船用挖掘机机械臂结构近似处理成含末端集中质量的柔性悬臂梁,建立了含时变参数的船用挖掘机机械臂系统虚拟样机模型,分析机械臂的动态性能,研究结果可以为进一步研究机械臂工作稳定性及运动精度控制提供依据。郭宇飞等[10]建立了坦克弹药传输机械臂刚柔耦合动力学模型,研究了负载变化情况下弹药传输机械臂的位置控制与柔性振动抑制,对于柔性振动和刚性运动分别采用速度反馈控制和连续时变增益PD控制实现弹药传输机械臂点到点位置控制及柔性振动抑制。Ma等[11]针对带有集中变质量的悬臂梁结构采用LQG控制器实现了系统的振动主动控制,但是需要求解时变的Raccati方程,模型复杂,计算量大。
模糊控制对那些数学模型难以获取,动态特性不易掌握或变化非常显著的对象非常适用。模糊控制系统的鲁棒性强,干扰和参数变化对控制效果的影响被大大减弱,尤其适合于非线性、时变及纯滞后系统的控制[12-14]。而PID控制器原理简单,使用方便,适应性强,鲁棒性强。结合模糊控制和PID控制优点的模糊PID控制算法,可以在线调整PID参数,使控制系统的响应速度快,过渡过程时间大大缩短,超调量减少,振荡次数少,具有更强的鲁棒性和稳定性。Kuo等[15]在机器人柔性臂的振动控制问题中,采用一种双时间尺度的模糊控制算法,使机械臂的振动迅速衰减,有效的抑制了结构的振动。魏井君等[16-17]基于查表法设计振动模糊控制器,提出采用修正Fuzzy-PI双模控制方法,有效的抑制了悬臂梁的振动。曹青松等[18]提出基于模糊自整定PID算法的柔性臂振动主动控制方法,试验结果也验证了该算法的有效性。但是对于含变质量参数的柔性臂结构来说,由于结构自身的质量时变、刚度时变或阻尼时变等因素,使其动力学控制规律更加复杂。Aghababa[19]应用一种分数阶滑模控制策略,控制含不确定参数的结构的振动,算例表明该算法具有很强的鲁棒性。Sharma等[20]提出了一种新型的分数阶模糊PID控制器,比较了分数阶模糊PID控制器,分数阶PID控制器,模糊PID控制器和经典PID控制器的控制效果, 数值算例表明分数阶模糊PID控制器有更好的鲁棒性和控制效率。梁捷等[21]开展了参数不确定情况下柔性关节-柔性臂系统的动力学模拟和主动抑制分析,提出了一种基于虚拟力概念的自适应模糊全局滑模控制方案,并利用相关实验证实了该方法的可靠性和有效性。针对系统的变质量特性,本文拟采用模糊PID控制器来时变变质量时变系统的振动控制研究。主要工作如下:首先推导了含变质量构件的压电梁结构的运动方程,研究了系统的振动特性,然后采用PID控制器和模糊PID控制器对质量增大系统和质量减少系统两类变质量时变系统进行了振动控制研究。
1 动力学模型
图1 所示为一个粘贴有压电片的柔性梁结构,其中梁的长度为L,梁末端安装一个集中质量,该质量是时间的函数m(t),单位时间内流入或者流出的质量为dm,v(t)代表dm流入或者流出m(t)时的绝对速度,压电片长度为a,压电的位置用x1表征,载荷f(t)作用在x2处,研究中忽略梁的剪切变形,采用欧拉梁理论,计算中只考虑梁结构的弯曲振动。
如图1所示的含变质量参数的压电梁结构的运动方程为
EbIbKfεpeH(x)+f(t)δ(x2)
(1)

图1 粘贴有压电片的变质量-梁结构

(2)
根据压电材料的本构方程,εpe可以表示为
εpe=d31Va/ha
(3)
式中:d31和ha分别为压电应变常数和压电片厚度。因此压电片的作动力可以写成
fV=EbIbKfεpeH(x)=KVV
(4)
当图1所示的梁结构为悬臂梁时,边界条件为
w(0)=wx(0)=wxx(L)=0
(5)

EbIbwxxx(L)=0
(6)
根据模态叠加法(Mode Superposition Method,MSM),式(1)的解可为前n阶模态φi(x,t)和组合广义坐标qi(t)的形式
(7)
与时不变系统不同,φi(x,t)为瞬时模态,是时间的函数,因此在计算中涉及对时间微分的部分,必须考虑模态函数的导数。φi(x,t)的形式如下
(8)
当末端质量为常数时,Cj为常数,对于变质量系统,末端质量是随时间变化的函数,因此Cj为末端质量的函数,满足如下正交关系

(9)
式中:δij为Kronecker delta函数。βj为末端质量m(t)的函数
cosβjLsinhβjL)
(10)
将式(10)代入式(1),通过Galerkin方法可以得到变质量梁系统的振动控制方程

(11)

M=I
(12)
(13)
(14)
F=F[f(t),fV(t),φ]
(15)
本文主要研究质量线性时变系统,时变质量变化形式为m(t)=m0+γt,其中m0为初始质量,γ为一个表征系统质量变化率的参数。对于质量减小的系统,γ<0,对于质量增大的系统γ>0。数值计算中,对于质量增大的系统,梁末端的集中质量从0线性地增大到2 kg,对于质量减小的系统,梁末端的集中质量从2 kg线性地减小到0。
假设梁结构的材料为线弹性的,压电材料使用其x-z方向的压电特性,梁结构和压电片的材料参数,如表1所示。首先分别使用模态叠加法(MATLAB)和有限元法(ANSYS)计算了不同末端质量时系统的固有频率,如表2所示。从表2可知,使用两种方法得到的结果是一致的。但是模态叠加法求解动力学响应时,自由度少,计算效率更高,而且便于施加控制。

表1 材料参数

表2 不同末端质量时系统的固有频率
时变质量系统自由振动的位移响应曲线,如图2所示,使用模态叠加法和有限元法得到的结果对应一致,从图2可知,当末端质量减小时,位移幅值逐渐增大,而当质量增大时,位移幅值逐渐减小。这是由于质量变化引起了一个非结构阻尼项,该非结构阻尼项正比于系统的质量变化率,当dm/dt<0即γ<0时,质量减少相当于引起了一个非结构负阻尼,该负阻尼使得系统的振幅增大,反之,dm/dt>0时,质量增大相当于引起非结构正阻尼,使得系统振幅加速衰减。

(b) dm/dt>0
2 模糊PID振动控制器
PID是工业控制中应用最广泛、技术最成熟的一种控制方法,经典PID控制器设计,如图3所示。它根据给定值r(t)与实际输出值y(t)构成控制偏差e(t)=r(t)-y(t),将偏差进行比例、积分、微分运算并通过一定规律的线性组合构成控制u(t)对被控量进行控制,满足:
(16)

图3 经典PID控制器
式中:比例系数kp,积分系数ki和微分系数kd往往是固定的。而对于变质量时变系统,系统的质量参数随时变化,使用经典PID控制器无法在整个时变过程中实现优化控制。而对于时变模型,通过模糊控制实时的调节反馈参数,可以有效的提高控制效果,更加适合时变系统的控制。
2.1 模糊PID控制器
在模糊PID控制器中,如图4所示。模糊控制器通过建立PID的反馈系数kp,ki,kd和输入误差e=r(t)-y(t)及误差导数ec=de/dt的模糊逻辑关系,实时得到反馈系数的修正值Δkp,Δki,Δkd,通过改进PID控制器的参数,提高控制效果,参数修正后,使用PID控制器作用于压电作动器,抑制系统的振动。
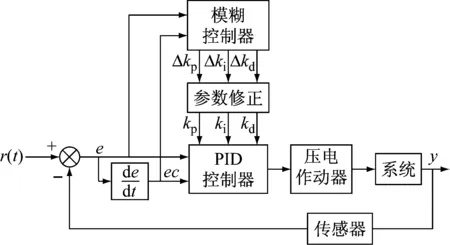
图4 模糊PID控制器示意图
2.2 模糊化
仿真中使用的模糊PID控制器为一个3输入(kp,ki,kd)2输出(e,ec)控制器,但是在模糊控制器设计中,无法直接识别这5个参数,因此在模糊控制器设计中,首先将这5个参数转化为7个模糊变量[NB,NM,NS,ZO,PS,PM,PB],子集中元素分别代表负大,负中,负小,零,正小,正中,正大,这一步称为模糊化。控制器设计中通过系统的振动特性定义输入值和输出值的取值范围,计算中e,ec,kp,ki和kd五个参数的定义域分别为[-6, 6],[-3, 3],[-0.3, 0.3],[-0.3, 0.3]和[-0.3, 0.3]。
2.3 模糊控制规则
Δkp,Δki和Δkd模糊控制规则,如表3~表5所示,在模糊模块中,重力模型和Mamdani算法被用来实现模糊变量的去模糊化。

表3 Δkp模糊控制规则表

表4 Δki模糊控制规则表
根据模糊控制率得到参数修正量Δkp,Δki和Δkd,因此经过模糊模块修正后的PID控制器的三个参数分别为
kp=kp0+Δkp
(17)
ki=ki0+Δki
(18)

表5 Δkd模糊控制规则表
kd=kd0+Δkd
(19)
式中:kp0,ki0和kd0为PID中比例参数、积分参数和微分参数的初始取值。通过模糊策略,在控制过程中,在线、实时的调节控制参数kp,ki,kd,使得PID控制器更适用于该变质量时变系统。
3 时频响应分析
在时变参数系统的振动信号处理中,使用Fourier 变换虽然可以得到信号的部分频域特征,但是无法得到系统共振频率和振动能量的时间特性。而时频分析技术以其强大的功能被扩展到诸多信号处理问题中,多种分布函数如Wigner-Ville分布,Choi-Williams分布等,被广泛应用机械设计、振动监测和故障诊断等领域[23-25],鉴于Choi-Williams分布函数信号密集性好、交叉项抑制能力强等优点,本文采用Choi-Williams分布函数来处理得到的非平稳位移响应信号。
圆锥型Choi-Williams分布函数的形式为
(20)
从式(20)可知,Choi-Williams分布通过建立时间t和频率ω的联合函数,描述信号同时在时间和频率的能量密度或强度,比FFT分析所得到的信息更加完整。其中Ax(η,τ)为Sussman模糊函数,用来修正原始信号,保证信号在时频分析中的稳定性。

(21)
φ(η,τ)为指数型核函数
φ(η,τ)=e-α(ητ)2
(22)
通过调整α值的大小可以控制时频分析的精度。借助MATLAB 时频分析工具箱,可以迅速得到时域信号的时频分解。
4 振动控制计算仿真
系统的振动能量主要集中在前几阶模态振动中,因此低阶振动的控制一直是主动控制的重点。给定图1所示的质量-弹性梁结构一个初始位移然后释放,在结构自由振动过程中,施加模糊PID反馈控制器,调节压电片控制梁结构的振动。通过数值模拟,首先计算了质量减少系统的振动主动控制,控制前后的位移响应曲线,如图5所示。对应的频响曲线,如图6所示。
从图5可知,施加PID和模糊PID控制后,系统的振动都得到了有效的抑制,对比这两种控制后的响应曲线,施加模糊PID控制后,系统的位移响应衰减的更快,说明使用模糊控制部分调节的PID控制器的参数,可以有效改善控制效果。由于系统质量减少,因此系统的频率增大。对比图5(a)和图5(b)中系统的响应曲线可知,kp0越大,反馈增益越大,控制效果越好,但必须保证压电片的驱动电压在使用范围之内,防止电压过大造成压电片的损坏。从幅值谱曲线上也可知,使用PID控制器,幅值下降了60%,而使用模糊PID控制器后,幅值下降了约为85%。
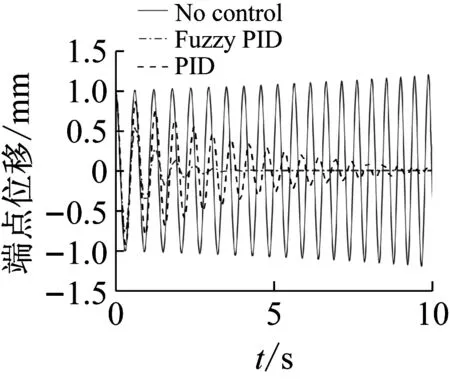
(a) kp0=0.5,ki0=0.05,kd0=0.05

(b) kp0=0.8,ki0=0.05,kd0=0.05
Fig.5 Displacement responses for decreasing mass system with and without control

(a) kp0=0.5,ki0= 0.15,kd0=0.05

(b) kp0=0.8,ki0= 0.15,kd0=0.05
Fig.6 Frequency responses for decreasing mass system with and without control
对图5(a)中的位移响应曲线做CWD(Choi Williams distribution),得到了图7中显示的控制前后系统位移曲线的时频响应谱。系统末端的集中质量从2 kg线性的减小到0,系统的振动频率从1.6 Hz增大到2.4 Hz,从图7(a)可知,系统的振动能量增大,这是非结构负阻尼的作用使得系统的动能增大,施加控制后,因此从能量密度谱上可以看出,系统的振动能量迅速减少,也就是说系统的振动得到了有效的控制。比较图7(b)和图7(c)可知,模糊PID的控制效果由于经典PID控制器。当β<0,kp0=0.8时,系统的时频响应谱图,如图8所示。现象与图7中所示的现象类似,但是由于施加的反馈系数更大,因此控制效果更好。

(a) No control

(b) PID
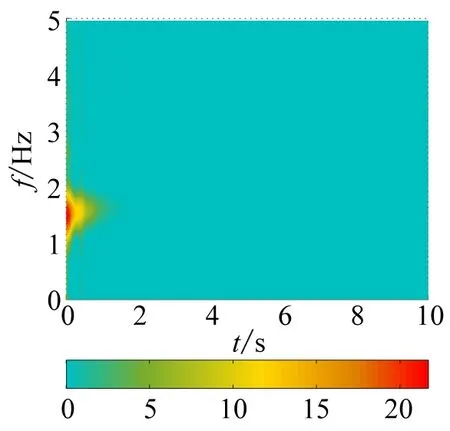
(c) Fuzzy PID

(a) No control

(b) PID

(c) Fuzzy PID
对于质量增大的系统,控制前后系统的位移响应曲线和幅值谱曲线,如图9和图10所示。类似的,从图中可知,施加PID和模糊PID控制后,系统的振动幅值迅速衰减,对比PID和模糊PID控制后的位移响应曲线表明,施加模糊PID控制后,系统的位移响应衰减的更快,说明模糊PID控制器自适应性更强,控制效果更好。从幅值谱曲线上也可以看出,使用PID控制器,幅值下降了54%,而使用模糊PID控制器后,幅值下降了约为83%。
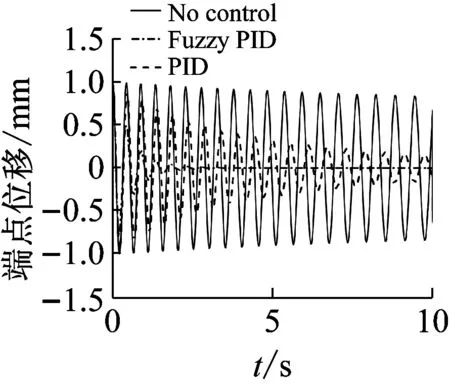
(a) kp0=0.5,ki0=0.05,kd0=0.05
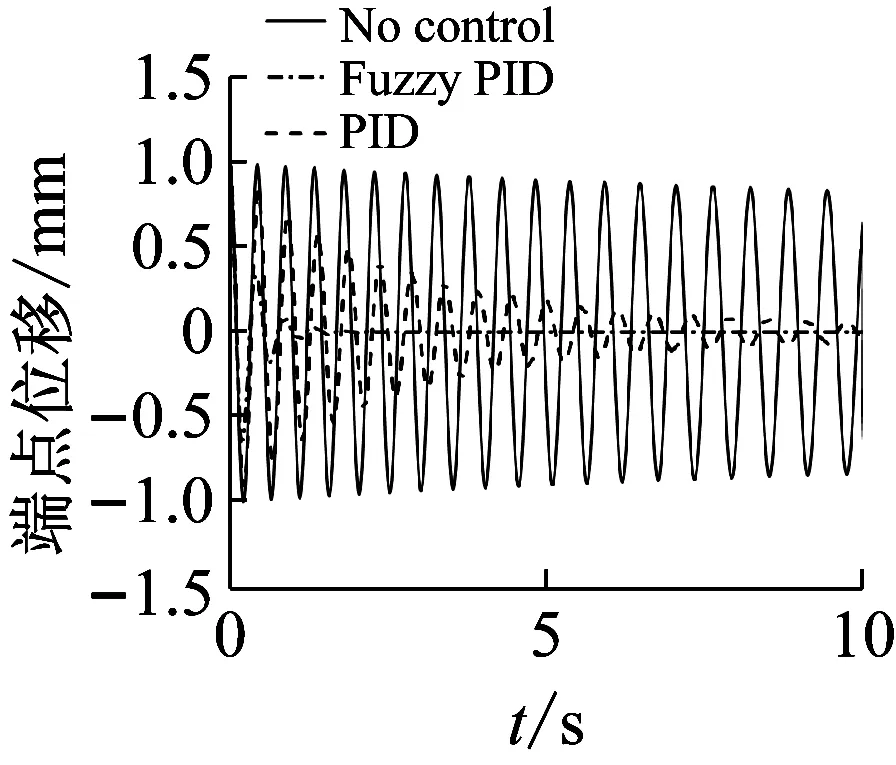
(b) kp0=0.8,ki0=0.05,kd0=0.05
Fig.9 Displacement responses for decreasing mass system with and without control

(a) kp0=0.5,ki0=0.15,kd0=0.05
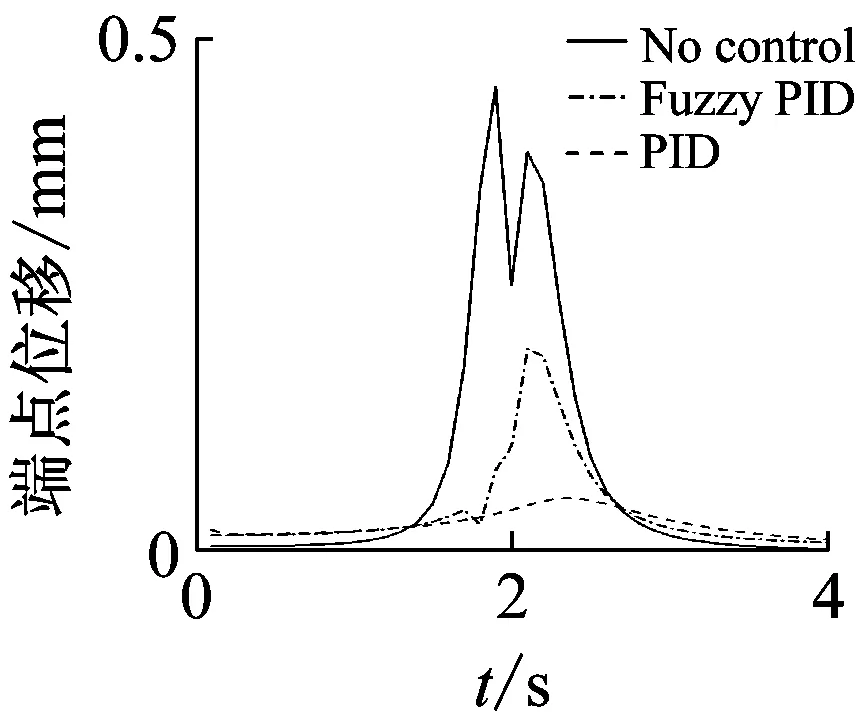
(b) kp0=0.8,ki0=0.15,kd0=0.05
Fig.10 Frequency responses for increasing mass system with and without control

(a) No control

(b) PID
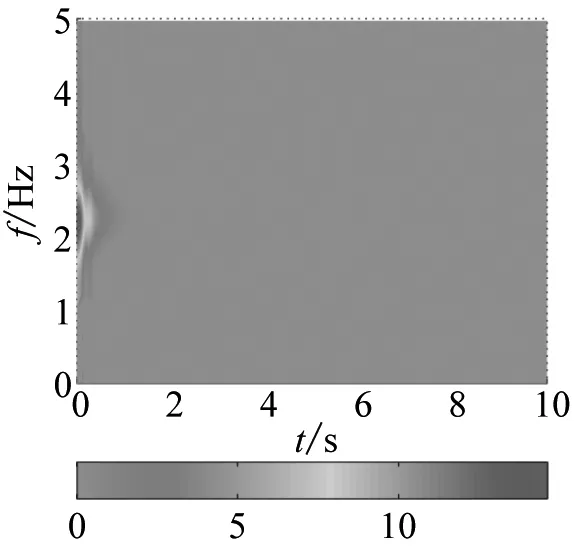
(c) Fuzzy PID

(a) No control
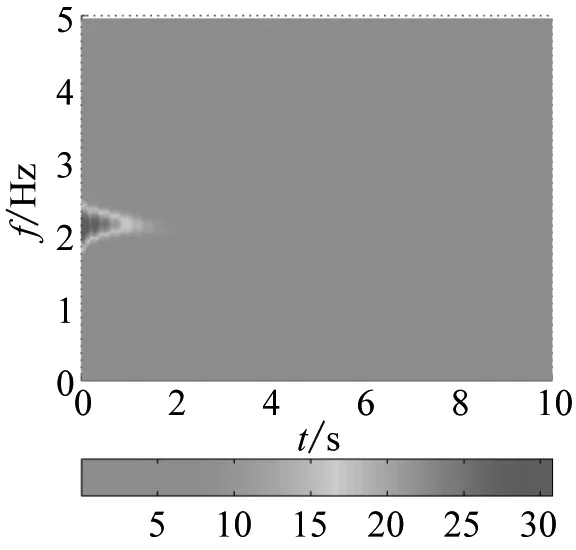
(b) PID
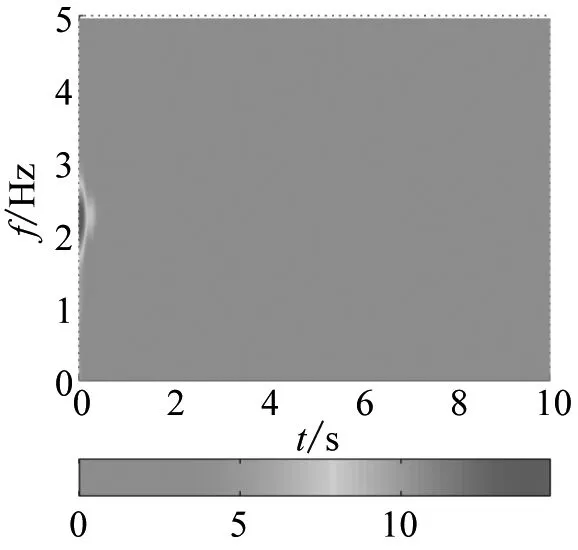
(c) Fuzzy PID
对图9中的位移响应曲线做CWD,得到了质量增大系统位移曲线的时频响应谱,分别如图11和图12所示。梁末端的集中质量从0增大到2 kg时,系统的振动频率从2.37 Hz降低到1.6 Hz左右,使用模糊PID控制,系统振动的衰减更快,同时增大反馈系数,也可以提升控制效果。
5 结 论
本文针对含变质量参数的柔性机械臂结构,推导了粘贴有压电片的变质量-欧拉梁组合结构的控制方程,研究了该类时变系统的动力学特性,并开展了振动主动控制研究,采用经典PID控制器和模糊PID控制器对变质量-弹性梁结构开展主动控制研究。主要结论如下:
(1) 通过模态叠加法和有限单元法得到的结果对比一致,验证了本文计算的正确性。对于变质量时变系统来说,质量变化使得系统振动频率变化的同时,会引起系统振动幅值的改变。这是由于质量变化会引起一个非结构阻尼,当系统质量增加时会引起一个非结构正阻尼,当系统质量减少时,引起非结构负阻尼。
(2) 使PID控制和模糊PID控制两种算法都可以实现系统的振动抑制,在关心频率范围带内都可以对结构的振动都得到了有效的抑制。但是使用模糊自整定PID控制器,鲁棒性高,自适应性强,通过改进PID控制器的参数,可有效的提高控制效果。
(3) 采用时频分析技术分析系统的响应信号,可以显示系统的时频特性,比FFT变换更有优势。

