考虑自由液面影响的有限长脉动圆柱远场声学分析

郭文杰, 李天匀, 朱 翔, 林子钦

(1.华中科技大学 船舶与海洋工程学院，武汉 430074； 2. 华东交通大学 铁路环境振动与噪声教育部工程研究中心, 南昌 330013； 3.高新船舶与深海开发装备协同创新中心，上海 200240； 4.船舶与海洋水动力湖北省重点实验室，武汉 430074)

近水面有限长谐振动圆柱辐射声波时，由于界面的反射作用，反射声波会在结构表面发生刚性散射，而散射声触及界面又会形成回波，继而在结构表面产生多次散射和在自由液面产生多次反射，并最终形成稳态声场。(反射是一种特殊的散射，因此该问题也称之为互散射问题)

半空间结构声振问题的研究多采用数值方法，尤其是边界元方法运用最为广泛。通过和镜像原理的结合，即对三维声学Helmholtz方程基本解的修正[1-3]，实现计及界面影响的耦合振动及声辐射性能计算。邹元杰等[4-5]基于有限元-边界元耦合计算方法分析了自由液面和刚性壁面对水下方箱振动频率的影响。此外边界积分方法也是比较常用的方法，Liu等[6]应用边界积分方法对半空间内声辐射和声散射问题进行研究。类似于半空间边界元方法的处理思路，Seybert等[7]通过修正Helmholtz方程基本解来消除无穷边界积分的难点，并将边界积分方法推广到1/4空间域。

对于半空间问题的解析方法研究较少，且研究的结构较为简单，多为球或者二维圆柱。由于辐射声和散射声数学表达式的相似性，多数文献将其统一表示，并不加以区分。基于镜像原理，反射声均可认为由虚源发出，故将所有辐射声和散射声及其反射声分为两类，即实源声和虚源声。依照此类思路，Huang等[8-9]研究了平面波入射下半空间球壳和二维圆柱的散射声场，Hasheminejad等[10-11]开展了有限空间简谐振动二维圆柱的声学特性研究工作。Avital等[12]通过施加分布载荷来控制结构振动从而改变半空间球壳的散射声场，即从主动控制的角度出发来进行减振降噪。

此外也有学者将声波分为四类：①实源弹性辐射声；②实源刚性散射声；③虚源弹性辐射声；④虚源刚性散射声。白振国等[13]由此建立了有限水深环境中二维圆柱壳的振动声学物理模型，考虑了散射声的影响并探讨了潜深对声场分布和衰减特性的影响规律；以白振国的模型为基础，张林根等[14]建立了近水面双二维圆柱壳声散射模型，并对片体间的相互声遮挡问题进行分析。由于划分声波时区分了辐射和散射的成分，有利于研究互散射效应与浸没深度的关系，这对研究有限域声学问题中关于结构与界面的互散射问题有重要意义。

目前多数文献[15-16]在分析有限半空间或波导环境目标散射问题时，通常都要忽略目标与边界的互散射(称之为单体散射模型)，比如文献[17]提到目标应不十分靠近波导边界时才可忽略目标与边界的互散射。因此究竟浸没深度是如何影响目标与边界的互散射，以及频率是否也是影响因素均值得深入研究。

此外，对于有限长圆柱结构，由于结构轴向有限而流体域轴向是无限的，难以得到声压的解析表达式，因此半空间有限长圆柱简谐振动时声场的解析研究尚属空白。本文通过傅里叶变换，将轴向坐标变换为波数域，易于得到声压的波数域表达式，并由此可通过傅里叶逆变换及稳相法推导出远场声压的表达式，实现了此类问题的解析求解。此外，本文方法是考虑了声波在结构表面与自由液面之间的互散射效应，即使靠近液面，计算结果也是准确可靠的。

1 理论分析

圆柱长度为L，半径为R，浸没深度为H。取圆柱正中心点为坐标原点O，对应直角坐标(x,y,z)以及柱坐标系(x,r,φ)，其中x表示轴向，r表示径向，φ为周向角(与y轴夹角)。P点为空间任意观测点，定义在球坐标(R0,θ,φ)下，其中R0为距离坐标原点距离，θ为观测角(OP向量与x轴空间夹角)，如图1所示。

图1 模型及坐标系

由于自由液面的存在，可以借鉴镜像原理进行分析，所有反射声可认为由虚源发出。虚源坐标系(x′,f′,φ′)与实源坐标系关于自由液面对称，如图2所示。

图2 镜像原理坐标系

本文采用傅里叶变换方法，将轴向x变换到波数域，构建新的壁面连续条件(因为结构在轴向有限但流体在轴向无限，为建立结构表面振速与流体在其表面速度的连续条件，需要假设圆柱两端有两个半无限长声障柱)，再进行逆变换即可求得声压表达式。

定义傅里叶变换及逆变换如下形式

(1)

1.1 模型一

声压可划分为实源声压Pr和虚源声压Pi，根据分离变量法，实源声压可以表示为

(2)

波数域流体声压满足Helmholtz方程

(3)

由式(3)可得到实源傅氏声压如式(4)的解

(4)

同理，虚源傅氏声压可以表示为

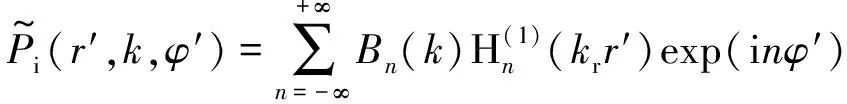
(5)

Bn(k)=-A-n(k)

(6)

为实现耦合方程的解析求解，需要将虚源声压由虚源坐标系迁移到实源坐标系。根据柱贝塞尔函数的Graf加法原理[18]可实现坐标迁移

(7)

式中：Jn()为第n阶第一类贝塞尔函数。

对于谐振动圆柱，径向位移有如下形式

(8)

同理将结构径向位移w变换到波数域，有

(9)

对于脉动振动，若脉动速度为v0，由于是简谐振动，速度幅值为位移幅值的倍，则

(10)

根据壁面处连续条件，变换到波数域，有

(11)

式中：ρf为流体密度。

将虚源傅氏声压迁移到实源坐标系下，因为r=R<2H，有

(12)

交换积分顺序后

(13)

(14)

通过傅里叶逆变换即可求出任意场点声压

(15)

对于远场声压，可以采用稳相法求解。稳相法是一种采用稳定相位点将无穷积分化简为简单的线性运算的数学方法，常用于物理学波场的无穷积分运算中。稳相法广泛的应用于声波[19]、光波[20]、电磁波[21]等相关问题的研究，适用条件是高频或远场。因为本文研究的是远场声辐射，因此稳相法也是适用的。限于篇幅，本文略去详细推导过程，直接给出球坐标系下声压表达式

(16)

式中：{An(kfcosθ)}可由式(14)求得。

1.2 模型二

(17)

式中：{En(k)}和{Fn(k)}可根据自由液面声压为零条件由{Cn(k)}和{Dn(k)}进行替换，如式(6)。

对于模型二，入射声Pinc可认为是由虚源发出，即

(18)

刚性散射声和入射声在结构表面处满足刚性散射条件，在波数域表示为

(19)

由上式可以得到声压幅值向量{Cn(k)}和{Dn(k)}之间的转换关系

{Dn(k)}=[Link]{Cn(k)}

(20)

其中[Link]为辐射声压幅值和散射声压幅值的迁移矩阵。

再根据弹性辐射条件

(21)

正交化处理后可以得到

(21)

同理可以根据稳相法求出四类声压表达式，形式如式(16)。代入Cn(kfcosθ)和Dn(kfcosθ)具体结果可以求出远场四类声压值。

2 数值计算

计算模型参数：圆柱总长L=1 m，半径R=0.2 m，流体密度ρf=1 025 kg/m3，流体声速cf=1 500 m/s。

2.1 收敛性分析

从式(14)和式(16)可知，要使得数值计算成为可能，需要对周向展开项数进行有限截断，因此需要对其进行收敛性分析。假设计算模型脉动速度10-6m/s，计算了R0=1 000 m，θ=π/3和φ=π/6时声压级随频率以及浸没深度的变化规律，如图3所示。

(a) f=200 Hz(b) f=500 Hz(c) f=1 250 Hz

图3 声压级收敛性分析

Fig.3 The convergence curves of the sound pressure level

从图3可知， 随着截断数N的增大，声压级均会趋于收敛。但是N取值大小与浸没深度H以及激励频率f有关。

此外，通过大量的试算发现截断项数N近似的与激励频率f和浸没深度H的乘积相关，具体的规律，如表1所示。

表1 需要的截断项数N

2.2 准确性验证

前文提及边界元方法可通过修正Helmholtz方程基本解进行半空间声学分析。因此，本文通过对比模方法准确性。半空间边界元方法基本思路如下。

Helmholtz半空间积分方程如下所示

(23)

取浸没深度H=4R、频率f=100 Hz和浸没深度H=2R、频率f=1 000 Hz两组工况，圆柱壳表面为脉动速度(表面法向速度均为10-6m/s)，观测点半径R0=1 000 m，观测角θ=π/4，周向角φ取-π/2～π/2。两类方法下计算结果对比，如图4所示。定义声压级SPL=20lg(|P|/P0)，单位dB，其中|P|为声压绝对值，P0=10-6Pa。

图4 本文方法和BEM计算结果对比

由图4可知，本文方法和边界元方法计算的声压指向性曲线吻合的很好，说明本文方法准确可靠。

2.3 两类模型统一性分析

为定量说明这个问题，取浸没深度H=2R和4R，频率f分别为100 Hz和1 000 Hz的脉动圆柱(表面法向速度均为10-6m/s)，计算两类模型在球坐标系(1 000，π/2，0)处场点的总声压。

从表2可知，模型一和模型二计算的总声压级一致，这也验证了两类模型本质是相同的。从公式推导可知，将所有速度连续条件或者刚性散射条件相加，都可以得到总声压引起的法向速度和结构表面法向速度相等这个条件。从物理意义上讲，模型二是将声压的弹性与刚性部分拆分。声波的两类划分方式本质是一样的，但是后者由于划分的更为细致，区分了辐射和散射的成分，有利于研究不同工况下结构与自由液面之间的互散射效应。

表2 两类模型总声压级对比

2.4 散射声与辐射声分析

对于给定的结构尺寸以及速度分布形式，声场散射声和辐射声与浸没深度以及频率有关。可以采用模型二分析此类问题，将实源散射声和其反射声之和定义为总散射声压Ps，将辐射声和其反射声之和定义为总辐射声压Pe，总声压Pt=Pe+Ps，声场中总散射声压Ps相比总辐射声压Pe越大，互散射效应越显著。

模型参数和速度分布不变，为使计算结果尽量与模型尺度无关，频率和浸没深度均无量纲化，定义无量纲频率为kfR，无量纲浸没深度为H/R。分别取kfR=0.1、0.5、2.5，H/R=1.25、5、20共9组工况，分析声压Ps、Pe、Pt的指向性。声场观测点：R0=1 000 m，观测角θ=π/4，周向角φ取-π/2～π/2，如图5所示。

由图5可知，频率一定时，随着浸没深度的增大，各类声压指向性图分瓣(极大值)越多；浸没深度一定时，随着频率增大，分瓣越多。这是因为虚源和实源声压在远场叠加会发生干涉，以两振幅相同而振动相位相反的脉动小球源为例[22]，中垂线即相当于自由液面(声压为零)。由激励频率和两球距离的乘积决定其指向性(分瓣特征)，而且乘积越大，分瓣越显著。

从图5还可知，尽管整体上辐射声量级明显大于散射声，但在浸没深度较小时(H/R=1.25)，散射声对声场的影响不可忽视，当浸没深度较大时(H/R=20)，散射声对声场几乎没有影响。此外，同一浸没深度下(比如H/R=5)，频率越低，散射声对声场影响越小；频率越高，散射声影响越大。

为进一步研究浸没深度如何影响场点声压，取模型参数和速度分布不变，场点位于球坐标系(1 000，π/2，0)处，分别取频率kfR=0.25、0.5、1和2，H/R从1取到20，分析总散射声Ps、总辐射声Pe、总声压Pt的声压级曲线随浸没深度的变化规律，如图6所示。

由图6可知，由于自由液面的存在使声波与其反射声发生干涉，出现类偶极子效应。若将问题简化为点源问题，在场点(1 000，π/2，0)处，虚、实源辐射声波的波程差为2H，若波程差为声波波长整数倍则声压趋于零，即kfH为π的整数倍时出现谷值，总辐射声压随浸没深度增大呈周期变化(无衰减)。散射声波也以相同的周期波动，不同的是，总散射声压随浸没深度增大而波动衰减，并且谷值点与总辐射声不同，存在相位差。这是因为散射声产生的根源是辐射声受到液面的反射而后作用到结构表面，因此散射声与辐射声相位并不一致，此外距离自由液面越远，虚源辐射声到达结构表面时量级越小，但是由于散射声也有干涉效应，因此是波动衰减。

此外，通过图6还可知，一方面在结构贴近自由液面时(H/R<2)，散射声相对量级比较大，互散射效应比较强烈。另一方面无量纲频率较低时，散射声随浸没深度增大衰减得很快，比如kfR=0.25时，浸没深度超过5倍半径以后总辐射声曲线与总声压曲线贴合得很好，散射声的影响几乎可以忽略，这与图4结论是一致的。

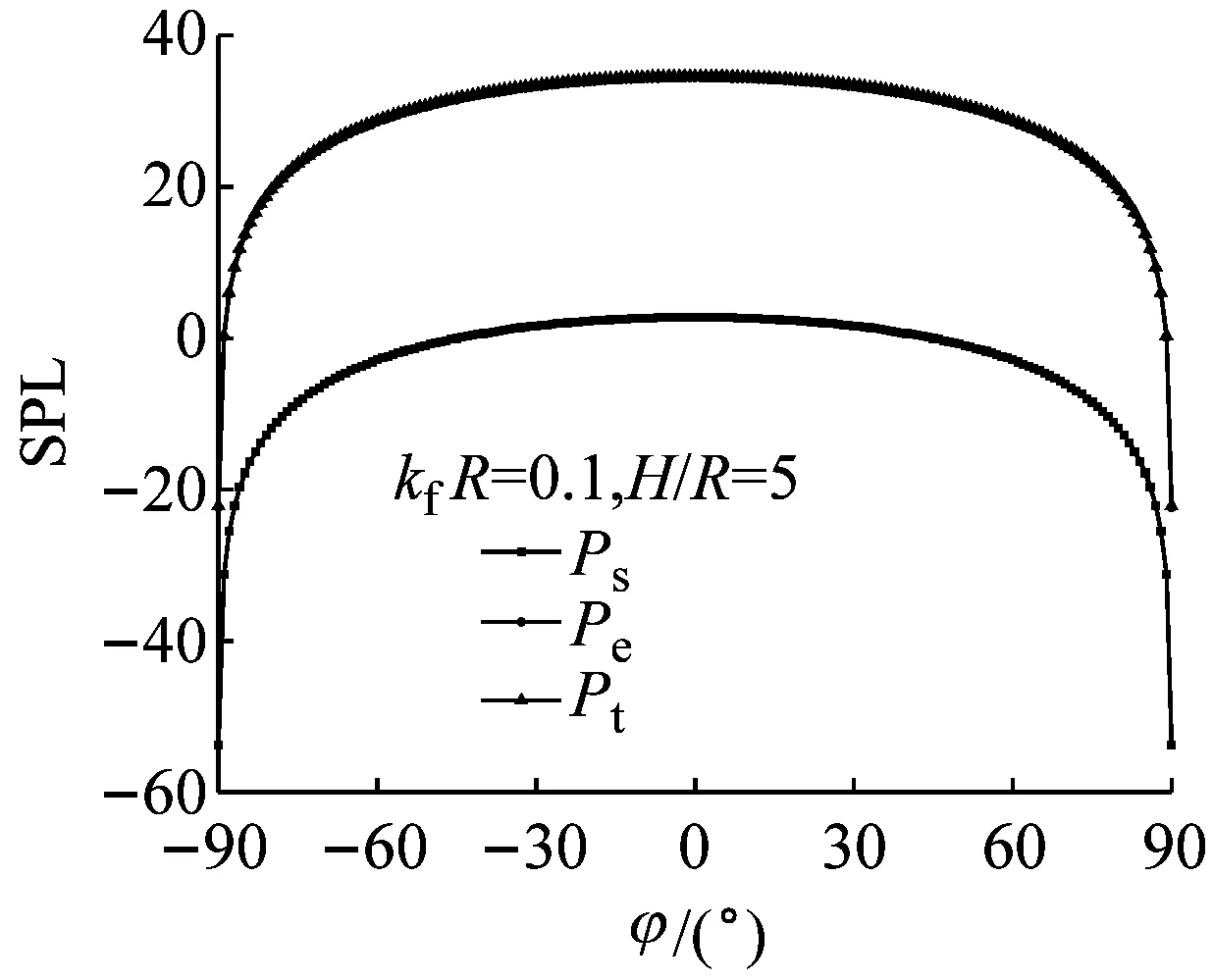
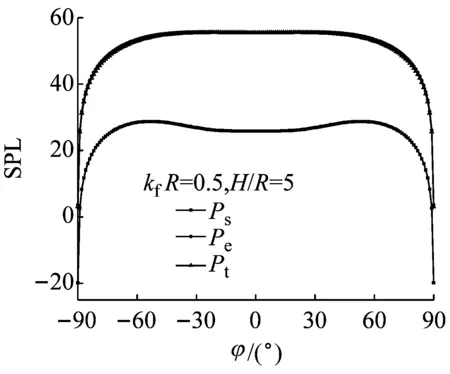
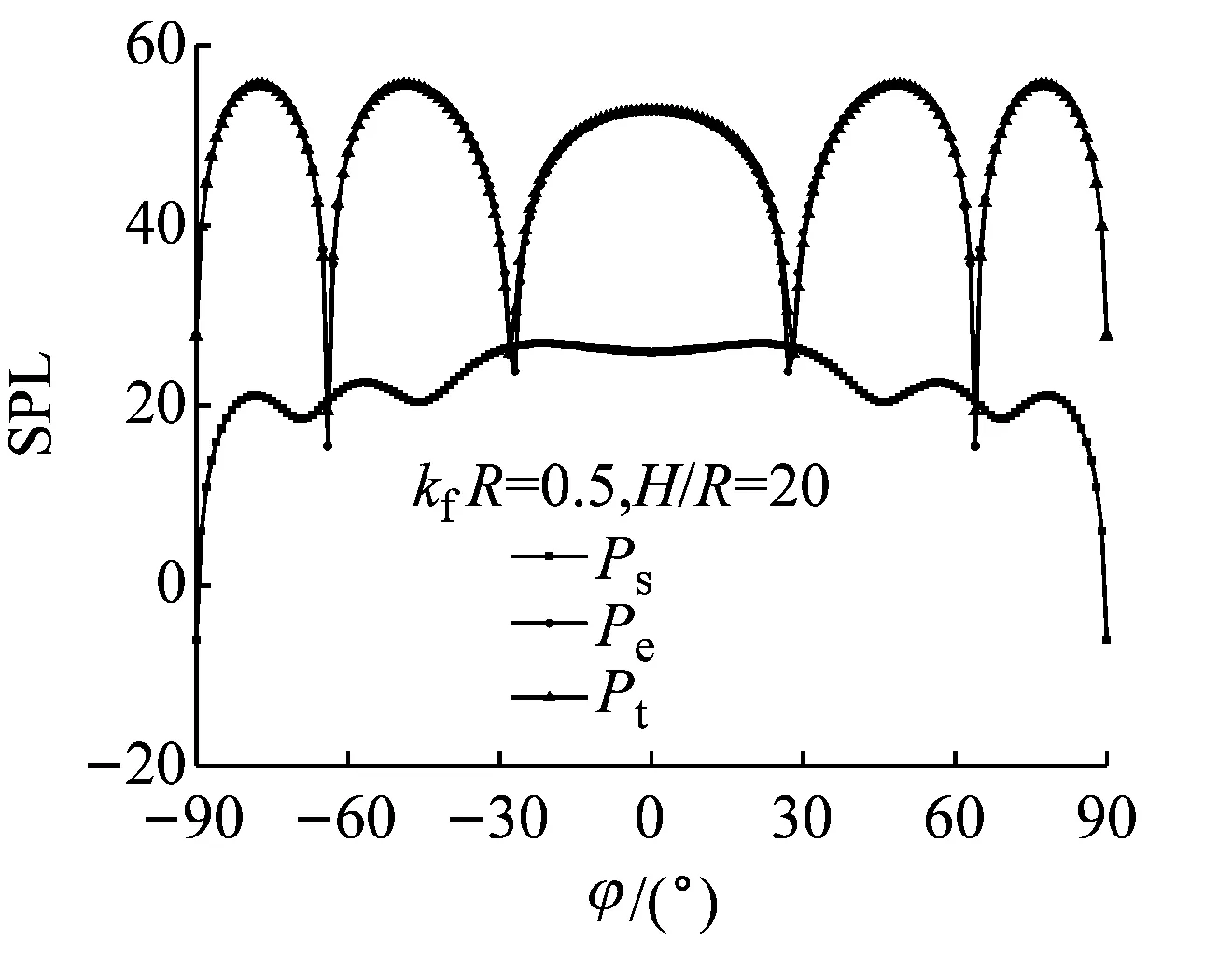
图5 散射声、辐射声、总声压指向性曲线

图6 散射声、辐射声、总声压随浸没深度变化曲线

水下结构辐射噪声时，高频声波由于波长较短，极容易受海洋环境影响而迅速衰减，因此本文主要针对低频互散射效应进行分析。定义指针互散射效应的参数η=|Ps/Pe|，当η<0.05时声场中散射声成分很少，认为互散射效应可以忽略。

取模型参数同上，场点处于(1 000，π/4，π/4)，分别取频率f=30 Hz、100 Hz、300 Hz(无量纲频率0.251)，计算互散射因子随无量纲浸没深度变化规律。

图7 不同频率下互散射效应因子随浸没深度变化曲线

Fig.7 Curves of the mutual scattering effect factors with the immersion depth change at different frequencies

从图7可知，随着浸没深度的增大，互散射因子很快降至<0.05以内，而且频率越低，互散射效应衰减得越快。当频率为30 Hz时，浸没深度>3.2倍半径散射效应可忽略不计；当频率为100 Hz时，浸没深度>3.4倍半径散射效应可以忽略不计；当频率为300 Hz时，这一数据则为4.1倍半径。因此对于低频问题，浸没深度在5倍半径以后，互散射效应可以忽略。

3 结 论

本文建立了半空间有限长脉动圆柱壳的两类数学物理模型，提出了其远场声压求解的解析方法。通过解析方法辨析研究了两类数学物理模型的异同，同时针对模型二开展了互散射效应研究，具体结论如下：

(1) 两类数学物理模型本质是一样的，但是后者区分了辐射和散射的成分，可针对互散射效应进行研究。

(2) 由于自由液面会带来类偶极子效应，随着浸没深度或者频率的增大，远场声压指向性图分瓣越多；场点的辐射声、散射声均会随浸没深度增大呈周期波动，但是散射声会波动衰减。

(3) 浸没深度<2倍半径时，互散射效应很强烈，散射声不可忽略。此外，频率较低时，浸没深度>5倍半径以后，互散射效应可以忽略。