漂浮式风力机结构动力学响应TMD控制及其参数优化研究
丁勤卫, 郝文星, 李 春, 叶柯华, 王渊博
(上海理工大学 能源与动力工程学院,上海 200093)
随着陆上风电场可开发资源的减少,海上风能因能量密度高和湍流度低等优势逐渐为世界各国重视,“由陆地向海洋”业已成为未来风电场发展的必然趋势[1-2]。目前,海上风电场主要集中在浅水区域,对于风资源更丰富、风况更优的深水区域,从经济性考虑必须采用漂浮式。海上风力机运行过程中需始终承受波浪载荷作用,这也是与陆上风力机的最大不同,因此,其载荷特性更加复杂。较之于固定式风力机,漂浮式风力机因底部基础不固定而导致的特有摇荡特性使得其始终处于受力不平衡、运动非定常状态,似此非线性载荷不仅影响机舱内传动系统的正常工作,亦会降低风机的发电效率,甚至可能导致塔架的屈曲、倾覆等事故[3-5]。此外,与传统海工平台相比,漂浮式风力机平台重心位置更高、水线面更小,波浪激励更加剧了平台的运动甚至倾覆。因此,研究漂浮式风力机在复杂多变的在役海洋环境中的安全稳定运行具有理论和应用价值。
目前,国内外学者针对漂浮式风力机稳定性问题展开了一些研究。文献[6]提出将螺旋侧板应用于漂浮式风力机Spar平台的结构设计中,并采用势-黏结合方法研究螺旋侧板对Spar平台动态响应影响,发现螺旋侧板可明显增大其稳定性。文献[7]针对漂浮式风力机对风浪激励响应过大问题提出了共用系泊的大型漂浮式风电场概念设计,并基于AQWA研究其运动响应特性,发现共用系泊可明显增大平台稳定性。上述研究不足之处在于将叶片、塔架及平台等结构简化为刚体,风载荷简化为轴向推力,显然这种简化无法精确描述非定常气动载荷,更无法揭示风浪激励下塔架、叶片等结构的变形、屈曲等非线性动力响应过程。
部分学者通过控制叶片变桨和电机变扭矩以降低叶片气动载荷进而达到提高漂浮式风力机稳定的目的。例如,Namik等[8]提出针对漂浮式风力机的叶片独立变桨技术,研究独立变桨对平台运动的控制效果,结果表明独立变桨降低平台运动的幅度可达39%。再如,Fischer等[9]提出一种基于加速度反馈的非线性控制方法,在理论上分析漂浮式风力机的稳定性。上述方法虽可在一定程度上增大漂浮式风力机稳定性,但会加剧叶片根部疲劳载荷。
此外,一些学者提出将主动结构控制技术应用于提高漂浮式风力机稳定性。例如,文献[10]建立了风波联合作用下Spar平台漂浮式风力机AMD控制系统运动方程,并利用最优二次控制算法实现对风力机纵荡运动的主动控制。主动控制技术虽可取得比被动控制更好的效果,但主动控制不易实现且成本高昂。此外,现代风力机作为人类目前建造的最大的旋转机械其结构巨大,主动控制时所需控制力非常巨大,已有学者指出,采用被动控制技术最适合于漂浮式风力机结构控制[11]。
调频减振装置主要包括:调频质量阻尼器(Tuned Mass Damper,TMD)和调频液体阻尼器(Tuned Liquid Damper,TLD),其作为结构控制技术被广泛应用于高耸柔性结构设计中。实验及数值计算均表明其对高楼、电视塔等高耸柔性结构减振效果明显[12]。风力机塔架属典型高耸柔性结构,因此,部分学者提出将调谐减振装置应用于风力机被动结构控制领域。国内外学者针对TMD/TLD对提高风力机稳定性效果亦开展了相关研究。文献[13]将TMD应用于海上风力机塔架中,并采用有限元方法研究其对风力机塔架振动的减振效果,但其将风轮和机舱简化为塔尖堆聚非旋转集中质量,此简化无法获知叶片等结构的动力学响应,更无法描述叶片-塔架等结构的耦合振动效应。Gordon等[14-16]研究TMD对漂浮式风力机稳定性的影响,但其不仅未考虑外载荷作用,且其工作仅为自由振动分析。文献[17]借助开源软件FAST考虑风浪载荷影响研究了TMD对Spar平台漂浮式风力机稳定性影响,其工作虽然考虑水动-气动-结构耦合作用,但其并未对TMD参数进行优化分析。
综上所述,旨在提高漂浮式风力机稳定性的研究虽在漂浮式平台结构设计、系泊系统优化及TMD结构控制方面开展了一些工作,但是:①多数研究均做了适当简化,漂浮式风力机系统是复杂的强耦合非线性系统,如叶片挥舞-塔架前后振动耦合,如叶片摆振-塔架左右振动耦合,对结构、自由度等的简化无法描述气动-水动-结构耦合作用;②显然,TMD控制效果与其固有质量、弹簧刚度及阻尼器阻尼均有关,但上述研究并未涉及其结构参数优化,因而导致其对振动位移及载荷等指标抑制率并不明显;③目前国内外学者针对提高漂浮式风力机稳定的研究大都基于张力腿平台、Spar平台等,基于Barge平台漂浮式风力机的甚少。
因此,本文借鉴相关学者研究经验,提出将TMD结构控制技术应用到提高Barge平台漂浮式风力机稳定性的研究中,进一步采用多岛遗传算法(Multi-Island Genetic Algorithm,MIGA)对所配置TMD的参数进行全局优化,以期为海上漂浮式风力机的稳定性控制提供一定的理论参考。
1 研究对象
本文研究对象为基于ITI Barge平台NREL 5 MW风力机,风力机参数[18]如表1所示。平台参数[19]如表2所示。漂浮式风力机模型,如图1所示。
2 研究方法及TMD控制
基于NREL开发的气动弹性结构动力学仿真软件FAST研究TMD对漂浮式风力机的结构动力学响应影响,相关学者采用FAST对风力机结构动力学响应进行仿真分析并将计算结果与GH-Bladed进行对比发现二者计算结果具有极高的吻合度,可验证FAST计算结果准确可信[20]。

表1 NREL 5 MW风力机参数

表2 ITI Barge平台参数
FAST考虑气动-水动-结构-控制耦合基于时间推进方法实现对非线性运动方程的求解[21-22]。气动模块基于Pitt-Peters动态入流理论并考虑轴向及切向风诱导的影响求解风轮平台诱导速度,进一步基于叶素动量理论考虑叶尖损失、轮毂损失及Beddoes-Leishman动态失速模型修正求解风轮气动力;水动模块计算漂浮式平台的水动力载荷,包括水线面面积矩和浮力;针对大尺度结构采用辐射/绕射理论求解波浪力,针对小尺度结构采用Morison方程考虑黏性效应和附加质量效应影响,但无法考虑VIV(Vortex Induced Vibration)激振力;系泊系统采用悬链线模型。弹性模块通过Kane方法结合模态法并考虑子结构刚柔特性建立风力机多体动力学模型,其中叶片、塔架及低速传动轴为柔性体模型,具有分布的质量、刚度及模态,而将轮毂、高速传动轴及机舱等视为刚性体模型。以气动模块求解气动力及水动模块求解的水动力作为输入激励,得到该时间步的结构动力学响应并反馈至控制模型、水动模块及气动模块,控制模块则根据结构模块反馈信息作出相应的控制策略,如变桨控制、偏航控制及TMD控制等。具体仿真流程,如图2所示。

图1 Barge平台漂浮式风力机示意图
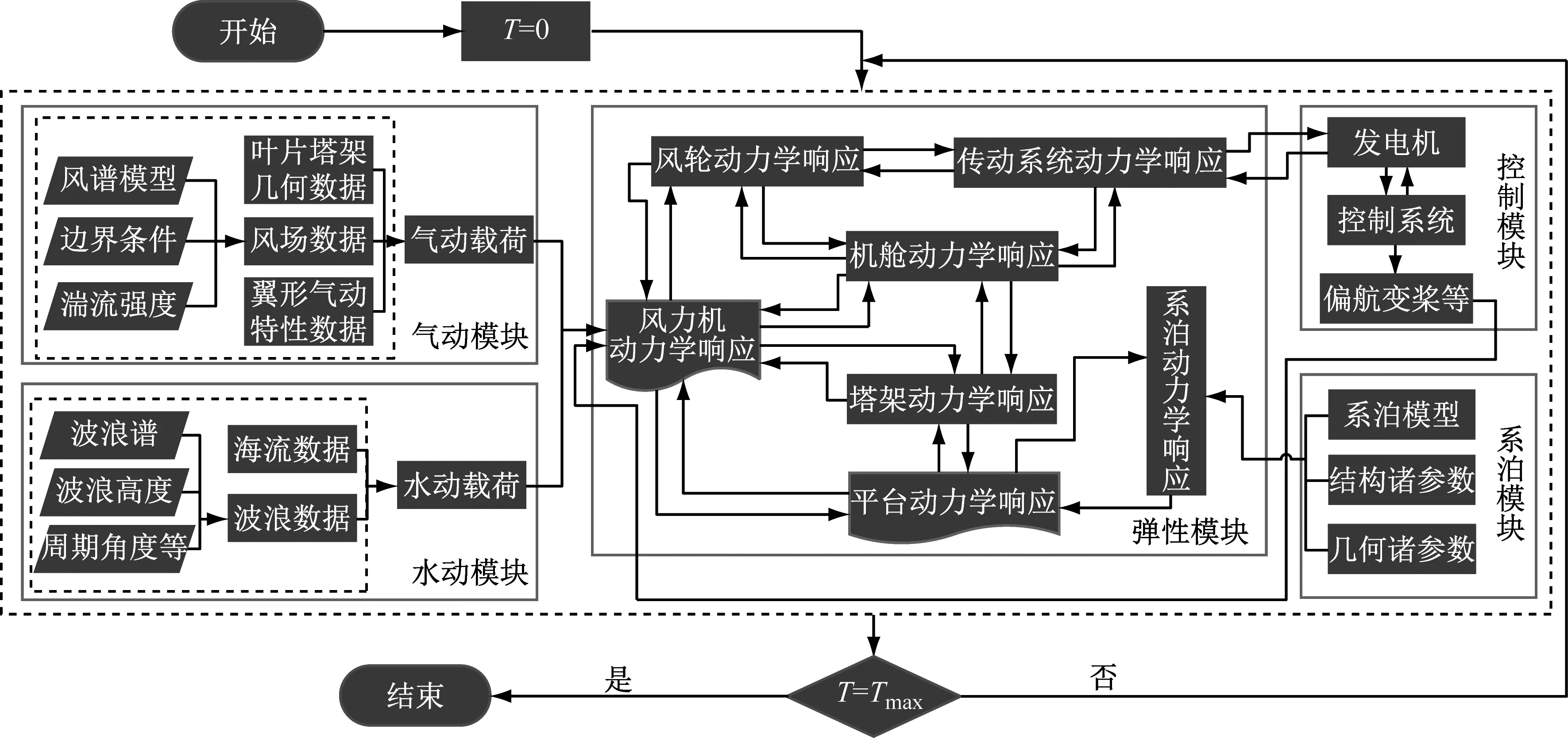
图2 仿真流程图
TMD由质量系统、弹簧系统、阻尼系统及支撑系统组成,其通过改变自身阻尼或刚度来达到调整自振频率的目的,使其接近被减振结构的固有频率或外部激励频率,当结构在外部激励下产生振动时,将带动TMD振动,TMD产生的调谐惯性力将反作用到结构上,并通过阻尼系统将能量耗散,以达到结构稳定性控制的目的。本文将TMD布置在机舱内部示意图,如图3所示。

图3 机舱布置TMD示意图
3 湍流风场及不规则波建模
3.1 风场模型建立
为更真实模拟时域高风速湍流风作用下漂浮式风力机的结构动力学响应特性,建立随时间及空间均变化的湍流风是仿真首先需要解决的问题。目前,常见的风场建模方法有:①基于测风塔实测数据,通过模糊逻辑预测、神经网络预测等方法得到一定空间范围内风速分布,该方法针对小空间风场建模较为准确,若要针对大空间风场建模,需要极度丰富实测数据,成本较高;②基于LES方法,考虑大气边界层效应等实现风场建模,但该方法所需计算资源极大;③基于风电场实测数据,通过气象分析方法获得风场风速分开,但该方法同样适合小尺度空间风场建模,针对大尺度空间风场建模误差较大。鉴于此,本文基于Kaimal风谱并考虑空间相干性建立三维时变风场模型。
根据所研究风力机几何参数,设定风场覆盖区域为195 m(水平方向)×195 m(垂直方向),之所以风场区域远远超过风轮扫略区域,是因为本文研究对象为漂浮式风力机,漂浮式平台六自由度运动导致叶片存在垂荡、横荡运动,为保障所建三维风场始终完全覆盖叶片,故将风场布置较大。进一步设定网格节点为15×15,如图4所示。考虑空间相干性,通过Kaimal风谱获得每一节点的风速分布,进一步通过空间相干模型获得整个风场的风速分布。空间相干模型如下
(1)
式中:Si,j(f)为节点i,j的互功率谱;C(Δr,f)为空间相干大小,节点之间距离为Δr;Si,i(f)Sj,j(f)分别为节点i,j的功率谱。
以轮毂中心为参考点,以时历平均风速11.4 m/s为参考风速,仿真时间为600 s,建立三维时变湍流风风场,轮毂高度处三维风速分布,如图5所示。轮毂点时域风速分布,如图6所示。由图6可知,所建湍流风在u方向波动范围为10.52~12.55 m/s,v方向波动范围为-1.052~0.993 2 m/s,w方向波动范围为-0.637 8~0.664 8 m/s。其中u方向为来流入射方向,v方向水平方向,w方向为垂直方向。
图4 风场计算区域及网格划分

图5 轮毂高度处风速分布
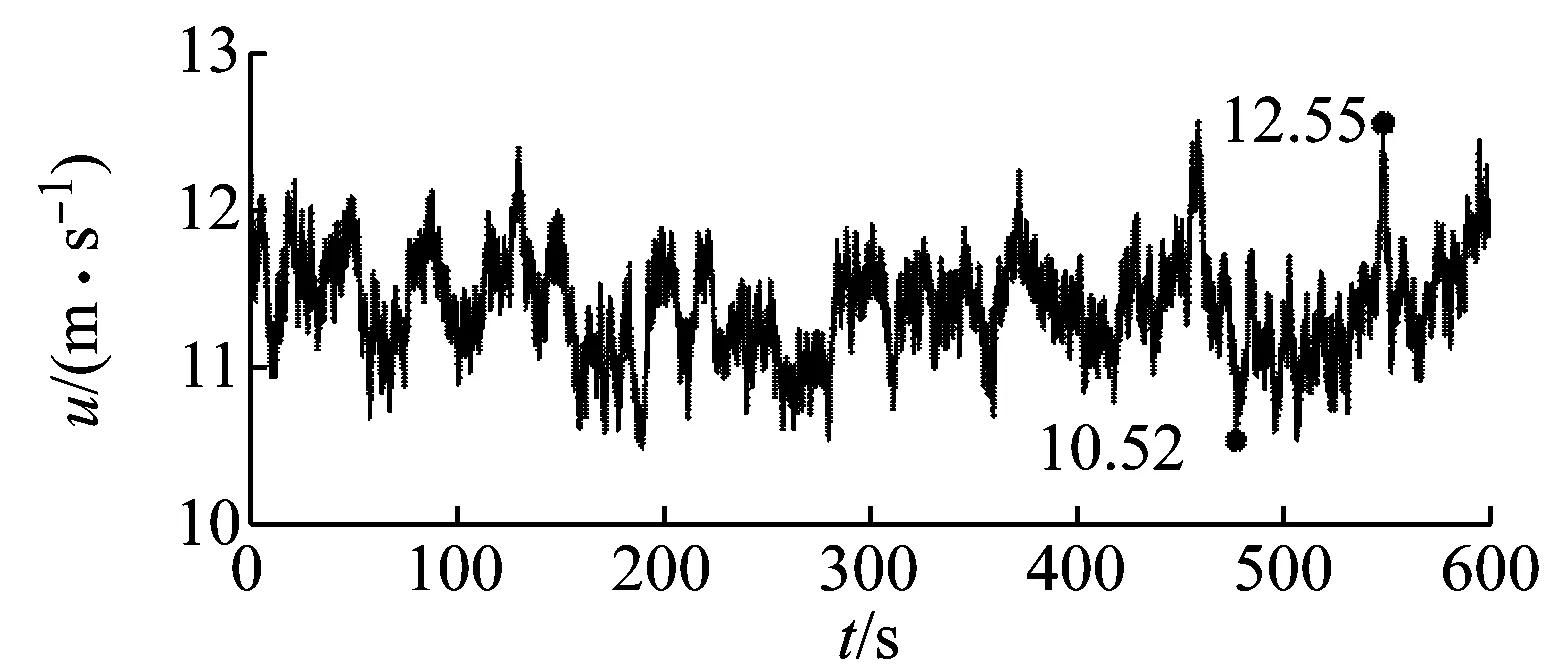
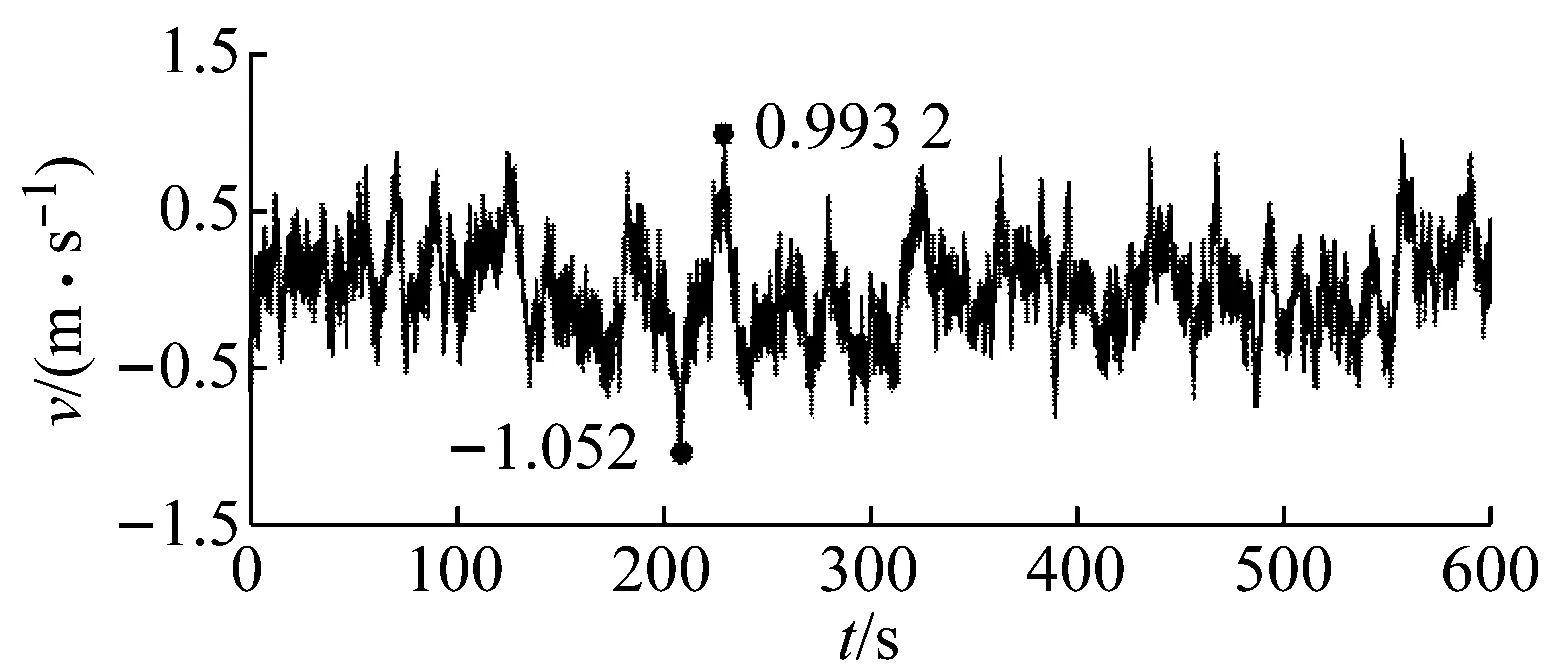

图6 轮毂点时域风速分布
3.2 波浪谱及不规则波浪建模
波浪谱以风因素和波浪因素为参量,通过定义有义波高、波浪周期及有限风区等参数即可得到波浪的大致形式。波浪谱是随机波浪的重要统计信息,可直接给出波能相对频率和方向的分布。国内外学者所做海洋结构的研究针对波浪载荷的考虑几乎全部采用波浪谱方法[23-27]。目前,常见的波浪谱有P-M谱、Jonswap谱和布氏谱等[28]。其中P-M谱根据大西洋波浪统计数据分析得出,其适合描述充分发展的波浪[29],其形式为
(2)
式中:U为某参考高度处平均风速;g为重力加速度;ω为波浪圆频率。
选取P-M波浪谱生成有义波高为5 m,谱峰周期为12.4 s的波浪,基于设定参数建立不规则波浪,如图7所示。
4 TMD对漂浮式风力机稳定性影响
4.1 TMD对平台摇荡特性影响
TMD结构控制技术广泛应用于高楼、电视塔等高耸结构,结构参数大都按照Den Hartog原则[30-31]确定,鉴于目前尚未有漂浮式风力机TMD结构控制参数设定的原则,故本文借鉴高楼、电视塔等设计经验,采用Den Hartog原则设定。此处TMD质量、阻尼及刚度质量为20 000 kg,刚度为10 000 N/m,阻尼为50 000 N/(m/s)。漂浮式风力机在TMD控制下平台摇荡特性的时程图,如图8所示。其中横坐标为时间,纵坐标为平台各自由度运动响应。

图7 不规则波浪模型

由图8可知,TMD控制下,TMD控制前后,平台纵荡、垂荡及纵摇响应改变甚微,几乎未发生变化,但平台横荡、横摇及首摇响应变化较明显。横荡波动幅值由-1.03~1.12 m降低到-0.65~0.85 m,波动幅度降低约30%,横荡最大值由1.12 m减小到0.85 m。横摇波动幅值由-1.11~1.38°减小到-0.54~0.88°,波动幅度降低约40%,最大值由1.37°减小到0.88°。配置TMD前后,首摇运动虽发生较大变化,但运动幅度变化较小。由计算可知,TMD控制前后,平台横荡标准差分别为0.477和0.352,平台横荡稳定性提高约25%;平台横摇标准差分别为0.492和0.289,比较可知,平台横摇稳定性提高约40%。
由上述时域分析可知,平台纵荡、垂荡、纵摇和首摇的变化不明显。因此,此处仅给出横荡与横摇的幅值谱,如图9所示。其中横坐标为频率,纵坐标为幅值响应。
由图9可知,平台横摇的频谱峰值约为0.09 Hz,横荡峰值频率约为0.01 Hz。此外,平台的横荡和横摇频谱峰值减小非常明显,进一步从频域角度验证了TMD对平台横荡和横摇控制效果显著。

图9 平台横荡及横摇运动幅频特性曲线
4.2 TMD对塔架顶部位移影响
漂浮式风力机在TMD控制下的塔尖位移时程图,如图10所示。其中横坐标为时间,纵坐标为塔尖前后及侧向位移。
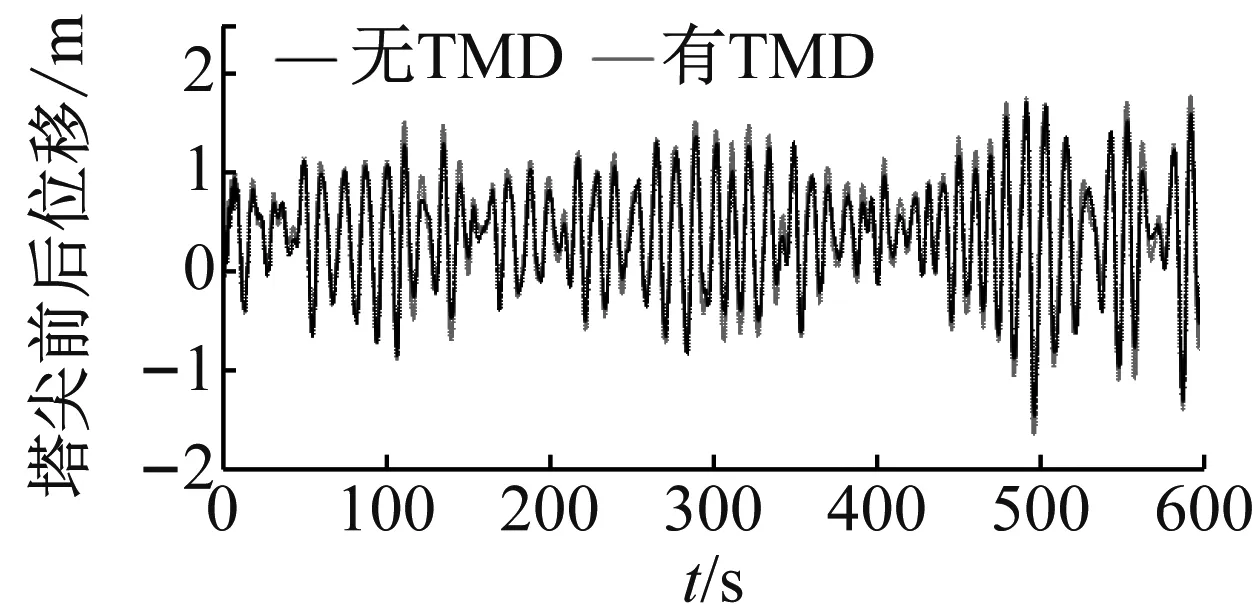

图10 塔尖前后及侧向位移时历曲线
由图10可知,TMD控制前后,塔尖前后位移均在-0.8~1 m之间无规律波动,TMD对塔尖前后位移影响甚微。配置TMD前后,前300 s差别不明显,300 s之后,TMD控制后塔尖侧向位移明显降低,且减小幅度非常明显。计算可知,TMD控制前后,塔尖侧向位移的标准差分别为0.066和0.041,塔尖侧向位移稳定性提高约38%。
对塔尖前后及侧向位移时域数据进行快速傅里叶变化,得到其幅值谱,如图11所示。其中横坐标为频率,纵坐标为幅值响应。


图11 塔架前后及侧向位移幅频特性曲线
由图11可知,塔尖前后及侧向位移的频谱峰值均约为0.09 Hz。比较有无TMD控制两种情况可知,无TMD控制时,塔尖前后及侧向位移幅值均大于受控时的幅值,但是塔尖前后位移幅值变化较小,而侧向位移幅值减小非常明显。
5 TMD参数优化
由前文时域及频域结果分析可知,机舱布置TMD对平台横荡、横摇运动及塔尖侧向运动起到明显的抑制作用,但影响TMD控制效果的参数包括质量系统质量、弹簧系统刚度及阻尼系统阻尼。TMD结构参数组合对优化漂浮式风力机稳定性效果必然不同,因此,探究较优的TMD结构参数组合对于提高漂浮式风力机的稳定性具有重要意义。本文采用多岛遗传优化算法对TMD结构参数进行优化,以确定较优的TMD结构参数组合。
多岛遗传算法[32]是在传统遗传算法基础上建立的一种基于群体分组的并行性遗传算法。多岛遗传算法将整个种群分解为多个子群(“岛”),并将各个子群互相隔绝于不同的“岛屿”上,对每个子群中的个体进行传统遗传算法操作(选择、杂交、变异操作),各个子群独立地进化,而不是全部种群采用相同的进化机制,并且各个“岛屿”间以一定的时间间隔进行“迁移”操作,使各个“岛屿”间进行信息交换。并且每隔几代挑选子群中的个体进行交换(迁移操作),保证了进化过程中优化解的多样性,从而有效抑制了早熟现象的出现,有利于找到全局最优解。
MIGA反复地使用算子和选择原则,从亲代到子代再到孙代直至重孙代不停地繁衍,从而种群对环境的适应性得到不断地升高。流程如下:
第1步 初始化群体;
第2步 计算个体的适应度函数值;
第3步 按个体适应度值决定的某种规则选择进入下一代的个体;
第4步 按概率Pc进行交叉操作;
第5步 按概率Pm进行突变操作;
第6步 若未满足停止条件,则转“第2步”,否则进入“第7步”;
第7步 输出种群中适应度值最优的染色体作为问题的满意解或最优解。
MIGA流程图,如图12所示。
目标函数:以漂浮式风力机塔架的塔尖侧向位移标准差σ1及平台的横摇标准差σ2之和最小为目标函数。
约束条件:
质量m:10 000 kg≤m≤40 000 kg
刚度k:5 000 N/m≤k≤25 000 N/m
阻尼d:6 000 N/(m/s)≤d≤21 000 N/(m/s)
优化设计所使用的MIGA算法控制参数中种群数、交叉概率、变异概率、迁移概率及最大代数分别为50、0.85、0.02、0.3和20。
6 TMD参数优化结果与分析
依据所设计的优化目标及多岛遗传算法参数设置方法,采用MIGA算法对计算结果进行优化,对质量、刚度及阻尼进行搜索寻优。

图12 多岛遗传算法优化流程图
图13为塔尖侧向位移标准差σ1值随质量m、刚度k及阻尼d样本点分布的四维云图。图14为σ1随质量m变化的剖面图。由图14可知,随着TMD质量增加,σ1变化较明显,呈现出先减小后增大的趋势,在15 000~25 000 kg区间内,塔尖侧向位移偏差σ1较小。进一步,将图14质量为15 000~25 000 kg间的剖面图局部细化,得到图15所示部分剖面图。由图15可知,当质量为18 695~22 935 kg区间内,塔尖的侧向位移偏差存在极小值;当阻尼取值不变时,σ1随刚度变化趋势较小,说明刚度变化对σ1影响不明显;当刚度取值不变,阻尼取值在12 000~17 000 N/(m/s)区间时,σ1存在明显变化。

图13 σ1四维图
图16所示平台横摇标准差σ2值随质量m、刚度k及阻尼d样本点分布的四维云图。图17所示σ2随质量m变化的剖面图。由图17可知,随着TMD质量增加,σ2变化较明显,呈现出先减小后增大的趋势,在20 000~30 000 kg区间内,平台的横摇偏差σ2较小。将该区域细化,得到局部剖面图,如图18所示。由图18可知,当质量取值在18 315~25 905 kg区间内,平台横摇的标准差σ2存在极小值;当阻尼取值不变时,刚度变化对σ2影响较小;当刚度取值不变,阻尼取值在12 000~17 000 N/(m/s)区间时,σ2存在明显变化。

图14 σ1剖面图
针对平台横摇运动,由图19可知,TMD控制后,平台横摇运动得到明显抑制,优化后TMD控制效果更好。优化TMD控制下,平台的横摇范围减小到-0.49~0.85°。由横摇运动时间序列数据计算可知,优化TMD控制后,平台横摇运动标准差约为0.23,均小于前文无TMD控制时的0.492和普通TMD控制时的0.289,平台稳定性提高约53%。结果表明,参数优化后TMD对平台横摇运动具有显著的控制效果。针对塔尖侧向位移,由图19可知,TMD控制后,塔尖侧向位移得到明显抑制,与对平台横摇运动的控制效果类似,优化后的TMD对塔尖侧向位移的抑制效果更好。优化TMD控制下,塔尖侧向位移波动范围为-1.53~0.071 m。由塔尖侧向位移时间序列计算可知,优化TMD控制后,塔尖侧向位移标准差约为0.034,亦均小于前文无TMD控制时的0.066和普通TMD控制时的0.041,塔尖侧向位移稳定性提高约50%。结果表明,参数优化后TMD对塔尖侧向位移同样具有显著的控制效果。综上所述,优化后TMD对平台横摇运动、塔尖侧向振动具有明显的抑制效果,计算结果与分析表明本文所提出的优化方法、优化算法及计算结果的准确性。
表3为MIGA算法优化后得到的TMD设计参数。为验证优化方法的可靠性及优化结果的准确性,依据优化结果重新配置TMD质量、刚度和阻尼并进行计算,结果如图19所示。为更清晰展示优化效果,此处选取300~600 s区间数据。


m=16 575 kgm=18 695 kgm=20 815 kgm=22 935 kgm=25 055 kgm=27 175 kg
图15σ1随m变化局部剖面图
Fig.15 A partial cross-section ofσ1

图16 σ2四维图

图17 σ2剖面图
7 结 论
本文以NERL的ITI Barge型漂浮式风力机为研究对象,采用在机舱配置TMD控制方法,考虑漂浮式风力机实际部署海域的风况与海况,研究环境载荷作用下漂浮式风力机无控和受控时的稳定性,后采用MIGA对TMD各参数进行全局优化,结论如下:
(1) TMD对漂浮式风力机塔尖侧向位移控制效果较明显,稳定性提高约38%;TMD控制下,漂浮式风力机平台横荡和横摇降幅明显。其中,平台横荡稳定性提高了25%,横摇稳定性提高了40%。
(2) 通过MIGA算法对TMD参数进行全局优化,结果表明漂浮式风力机的塔尖侧向位移及平台的横摇随TMD参数变化趋势相似。随TMD质量增加,均呈现出先减小后增大的趋势;当阻尼取值不变时,刚度变化影响不明显;当刚度取值不变,阻尼存在一定变化。
(3) 通过对比分析漂浮式风力机无控、普通TMD及优化后TMD的控制效果,验证了MIGA优化结果的有效性,可为海上漂浮式风力机配置TMD提供一定的理论参考。


m=15 605 kgm=18 315 kgm=21 025 kgm=23 735 kgm=25 905 kgm=28 615 kg

图18 σ2随m变化局部剖面图
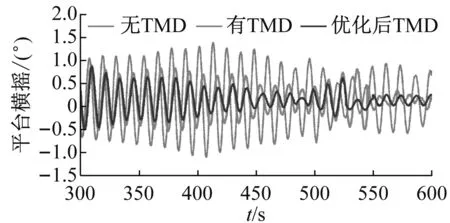

图19 优化后TMD对平台横摇及塔尖侧向位移影响

