含环向表面裂纹充液圆柱壳的耦合振动特性分析

金超超， 朱 翔， 李天匀， 方 敏

(1. 华中科技大学 船舶与海洋工程学院，武汉 430074； 2. 湖北省船舶与海洋工程水动力学重点实验室，武汉 430074； 3. 高新船舶与深海开发装备协同创新中心，上海 200240)

充液圆柱壳结构被广泛地应用于石油化工，船舶与海洋工程和土木建筑等工程领域，有大量文献对充液圆柱壳的振动特性进行了研究。Zhang等[1-2]通过波传播法研究了真空中和充液圆柱壳的自由振动特性，并与有限元和边界元方法的结果进行了对比，验证了其准确性。刘敬喜等[3]针对埋地管道研究了充液圆柱壳在弹性介质中的轴对称自由振动特性，其研究表明圆柱壳外围弹性介质会使得圆柱壳固有频率提高。Iqbal等[4]采用波传播法研究了多种边界条件下功能梯度圆柱壳的耦合振动特性。Amabili[5]通过添加虚拟质量的方法处理流体和结构的耦合作用，并采用传递函数法研究了圆柱壳的自由振动。郭文杰等[6]基于能量泛函变分方法和镜像原理，提出了有限浸没深度下圆柱壳振动特性的解析方法。受恶劣工作环境的影响，圆柱壳结构中往往会产生裂纹等损伤，造成安全隐患。裂纹的存在改变了结构的动力学特性，可以根据动力学参数的改变进行裂纹诊断。国内外学者就裂纹结构的振动开展了广泛的研究。由Rice等[7]首先提出的线弹模型已广泛应用于具有表面或内部裂纹的板和壳体的振动分析。Nikpour[8]用线弹簧模型研究了环向裂纹对圆柱壳对称振动的影响。彭凡等[9]基于铁木辛柯梁理论，结合线弹簧模型研究了含裂纹简支梁横向振动特性，并给出了裂纹位置识别方法。Zhu等[10-11]结合线弹簧模型，研究了含裂纹有限大平板和无限长圆柱壳的振动功率流特性，并提出了基于功率流的裂纹损伤检测方法。Yin等[12-13]针对含环向表面裂纹圆柱壳的振动特性提出了一种求解方法，其分析表明，短壳相比长壳对环向裂纹的存在更为敏感。罗志钢等[14]通过局部加权残量法将裂纹以虚拟边界引入，融入到系统振动特征方程中，通过测试固有频率识别悬臂梁裂纹深度。对于工程中应用十分广泛的充液圆柱壳结构，从已经发表的文献来看，目前尚无其含裂纹损伤情况下振动特性的解析研究。

本文针对含环向表面裂纹有限长充液圆柱壳的耦合振动特性提出了一种解析求解方法。根据Flügge[15]薄壳理论建立了充液圆柱壳的控制方程。利用线弹簧模型模拟环向表面裂纹。与文献和有限元结果进行了对比，验证了本文方法的准确性。讨论了裂纹参数对耦合振动特性的影响。

1 数学模型

1.1 研究模型

图1给出了含环向表面裂纹有限长充液圆柱壳的几何模型及参数。壳体材料密度为ρ；杨氏模量E；泊松比为μ；壳体厚度为h；半径为R；长度为L。所充液体的声速为Cf；密度为ρf。壳体在柱坐标系下x，θ，r方向上的位移分别为u，v，w。裂纹与壳体端部距离为cL；裂纹深度为a。

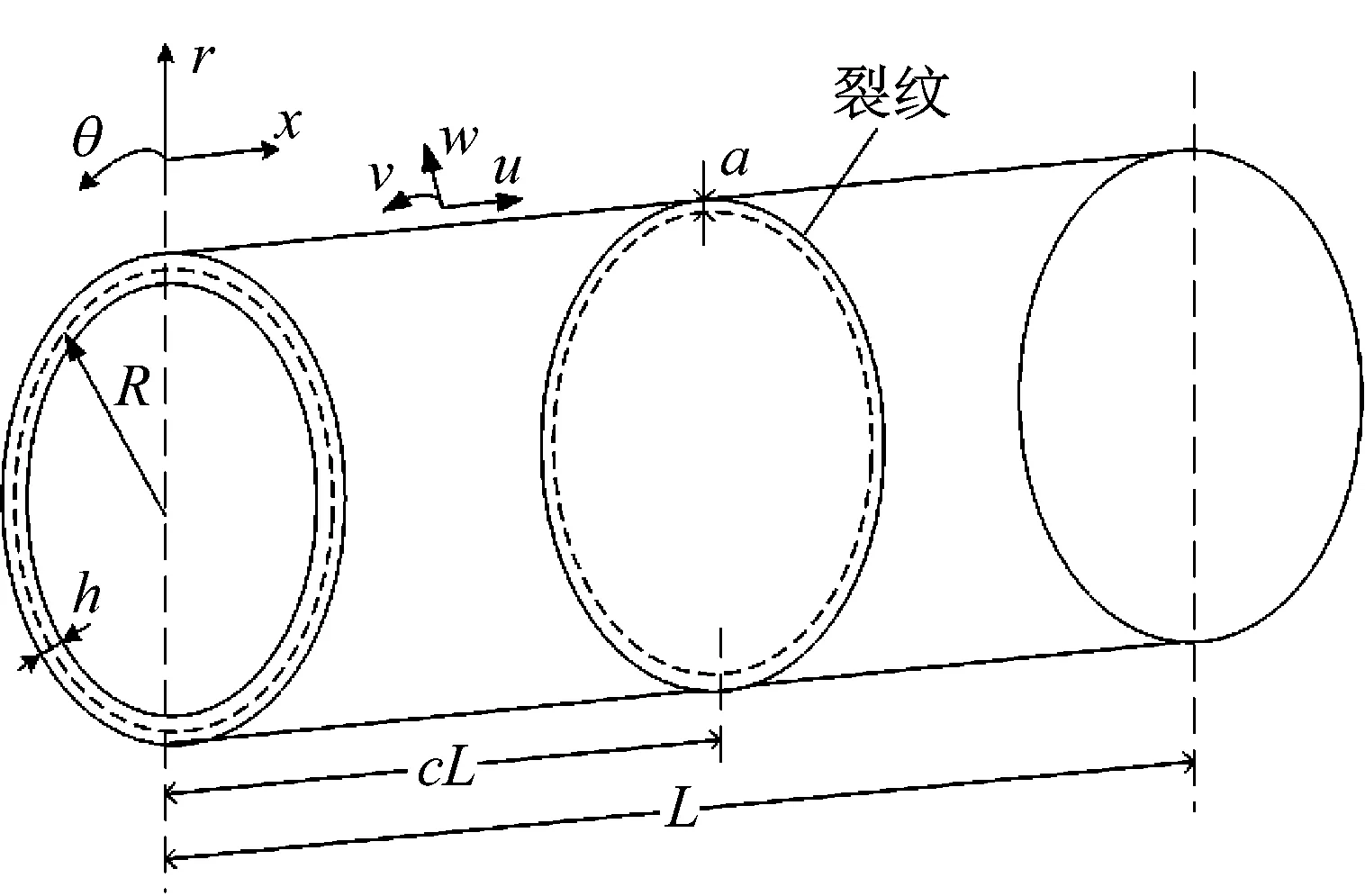
图1 含环向表面裂纹充液圆柱壳模型

1.2 控制方程

根据Flügge的理论，圆柱壳壳体微元的运动平衡方程可以表示为

(1)

式中：Pf为作用壳体表面上的流体声载荷。矩阵[L]3×3的各个元素如下

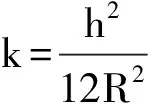
理想流体在柱坐标系下的Helmholtz波动方程为

(2)

基于波传播法，将壳体中面位移展开成为双级数简谐波形式为[16]

(3)

式中：ω为圆频率；n为周向模态阶数；kns为轴向波数；s为频散方程中轴向波数解的序号;Uns，Vns，Wns分别为轴向、周向和径向的位移幅值。

对于声压场，满足Helmholtz波动方程的流体声压有如下形式的解

(4)

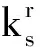
在流体与壳体的接触面上，流体径向速度必须等于壳体的径向速度，即

(5)

将式(3)和式(4)代入式(5)中可以得到对每一组(n,s)流体的声压幅值：

(6)

将式(6)代入式(4)，并将式(4)和式(3)代入式(1)中，便得到充液圆柱壳耦合系统的运动方程，用矩阵形式表示为

(7)

矩阵[T]3×3的各个元素如下

T33=-(1+k)-k(λ2-n2)2+2kn2+Ω2+FL

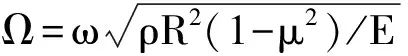
要保证式(7)中Uns，Vns，Wns有非零解，矩阵[T]3×3的行列式为零

|T|=0

(8)

1.3 边界条件和裂纹位置连续性条件

几种典型的边界条件：

自由端Nx=0,Mx=0,Sx=0,Txθ=0

简支端v=0,w=0,Nx=0,Mx=0

固支端u=0,v=0,w=0, ∂w/∂x=0

其中：Nx轴向力；Mx为弯矩；Sx为有效径向剪力；Txθ为有效周向剪力。

在x=cL处的部分穿透表面裂纹通过线弹簧模型来进行模拟。裂纹两边应满足内力连续条件，并且考虑由裂纹引起的附加广义位移

(9)

式中：下标l和r分别为裂纹位置的左右两侧。矩阵H4×4是由裂纹引起的局部柔度矩阵。H4×4中的每个元素如下

H21=H12;H31=H13;H32=H23;

H14=H24=H34=H41=H42=H43=0

式中：

F1=F4[0.752+1.287α+0.37(1-sinα)3]/cosα

F2=F4[0.923+0.199(1-sinα)4]/cosα

在平面应力状态下E′=E，平面应变状态下E′=E/(1-μ2)，k=1+μ

对于含环向表面裂纹有限长圆柱壳，需要同时考虑圆柱壳两端各4个边界条件，裂纹位置4个内力连续条件，以及裂纹引起的4个附加广义位移，写成关于径向幅值系数W的表达式，可以描述为以下16×16的矩阵

(10)

式中：W1，W2，…，W8为裂纹左端圆柱壳振动的8个径向位移幅值系数，W9，W10，…，W16为裂纹右端圆柱壳振动的8个径向位移幅值系数。为了保证这16个径向位移幅值系数有非零解，矩阵[G]16×16的行列式值应为零

|G|=0

(11)

2 计算方法

对于充液圆柱壳，由于式(7)中的流体载荷项中含有贝塞尔函数，系统的特征方程是复平面上的复数高阶超越方程，不能直接通过常规的实数方程求解方法求解式(8)来得到对应某个频率f的在复平面上的8个轴向波数。因此，这里采用一维优化迭代的方法。对于一个特定的频率，先计算出真空中圆柱壳的8个轴向波数作为初值，然后逐步将流体载荷项FL加入到控制方程中。以控制方程的特征行列式值作为为目标变量，采用割线法可以快速迭代收敛得到充液情况下足够精确的8个轴向波数。由于边界条件和裂纹位置连续性条件方程应满足式(11)的条件，为了高效地求解圆柱壳的固有频率，同样采用优化迭代的方法进行处理。计算方法的基本过程如下：

(1) 通过梁函数法计算对应边界条件下的固有频率初值；

(2) 设置流体载荷项为零，FL=0，由式(8)计算真空中的轴向波数k作为初值；

(3) 添加流体载荷，FL≠0，以行列式值|T|作为目标变量，通过迭代计算充液情况下的轴向波数k；

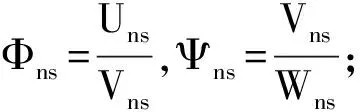
(5) 将轴向波数k和位移幅值比Φns，Ψns代入式(11)计算行列式值|G|；

(6) 以|G|作为目标变量，采用优化迭代算法计算满足该边界条件和裂纹位置连续性条件的耦合系统固有频率。

需要注意的是，对于某一模态周向波数n，有多个固有频率，分别对应不同阶次模态轴向半波数m，而且流体载荷的加入会使得圆柱壳固有频率有较大的变化，因此在整个迭代计算中，流体载荷项需要逐步添加上去以确保最后求得的固有频率值收敛于所求模态阶次(m，n)真实对应的结果。

3 方法验证

本节对本文的理论模型和算法进行验证。由于查阅文献尚未见到有关含环向裂纹的充液圆柱壳振动分析，为此本文对模型进行退化来验证方法的正确性。

首先，将裂纹深度a和流体密度ρf设置为0，模型退化为真空中完善圆柱壳，取圆柱壳几何和材料参数，如表1所示。

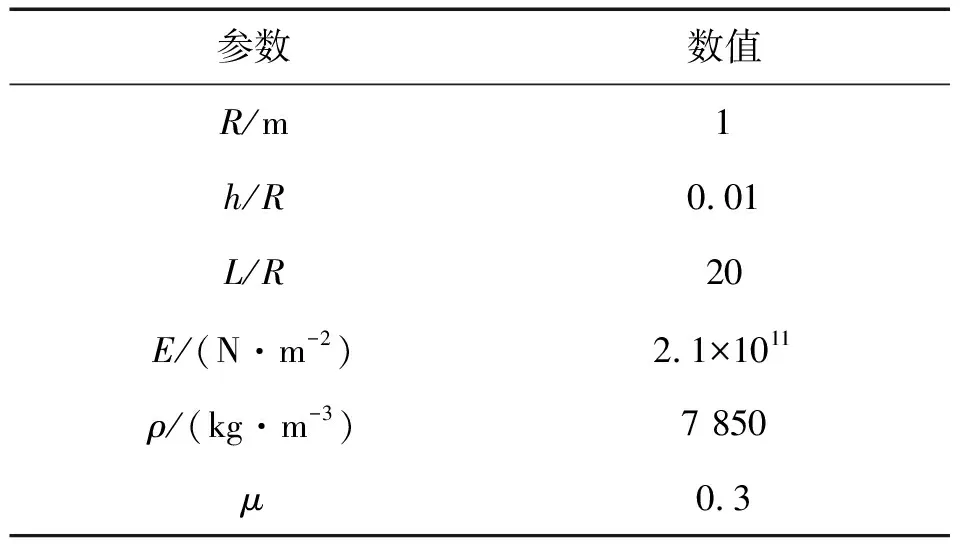
表1 圆柱壳参数

两端固支情况下本文方法和参考文献以及有限元前十阶固有频率对比结果，如表2所示。由表2可知，本文方法与文献和FEM方法的结果误差非常小，<0.1%。

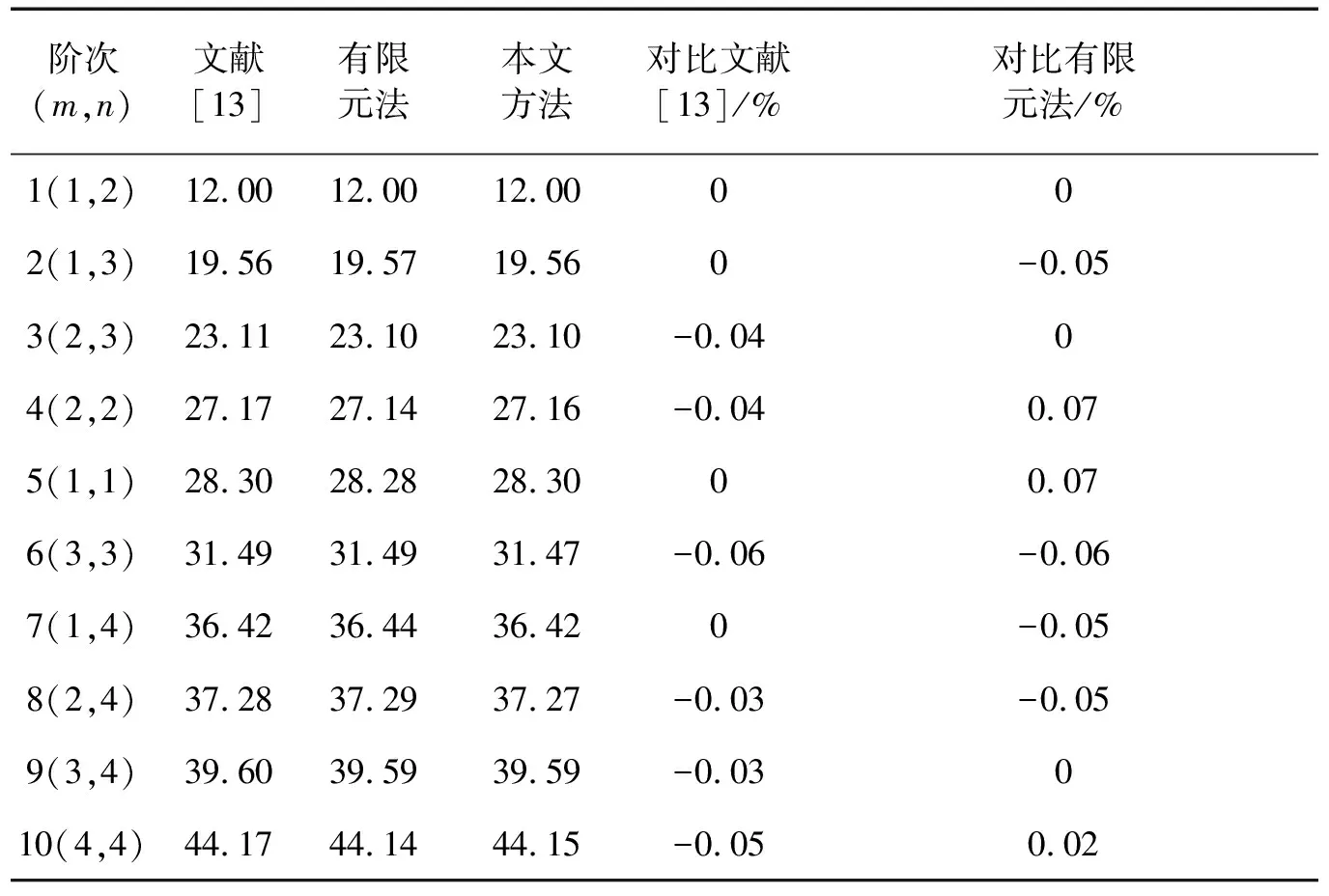
表2 真空中完善圆柱壳的固有频率

然后用本文方法来验证真空中含环向表面裂纹有限长圆柱壳的固有频率结果，裂纹参数为a/h=0.6，c=0.3，圆柱壳其他的物理参数与以上模型相同，与文献[13]的对比结果，如表3所示。

由表3结果可知，对于真空中裂纹圆柱壳模型，本文方法得到的固有频率和文献的十分接近，误差在1%以内。需要注意的是，对于以上研究的壳长比较大，壳厚比较小的圆柱壳，由于前几阶模态对应于圆柱壳的整体振动，局部位置存在裂纹引起的整体刚度减小并不明显，裂纹引起的固有频率改变相对较小。

最后将裂纹深度设置为0，所充流体的密度和声速分别为ρf=1 000 kg/m3，Cf=1 500 m/s，其他参数与前述相同，模型退化为充液完善圆柱壳，计算前8阶固有频率，并与文献[2]进行对比结果，如表4所示。

表3 真空中裂纹圆柱壳的固有频率

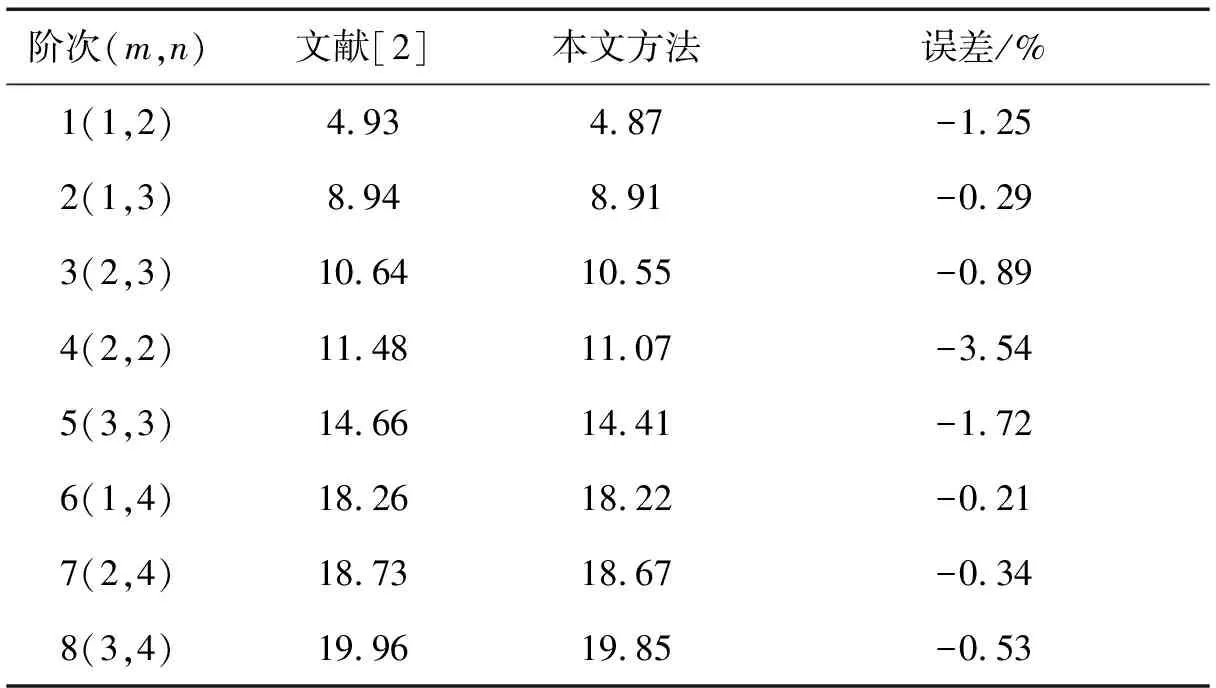
表4 充液完善圆柱壳的固有频率

由表4可知，对于充液完善圆柱壳，本文方法得到的固有频率与文献[2]吻合较好，误差大多<1%。比较表4和表2可知，流体载荷的引入会导致圆柱壳固有频率明显地减小。

由以上三个退化模型的对比验证可以得出，本文方法处理裂纹圆柱壳和充液圆柱壳的振动均和文献吻合较好，均有较高的精度，是一种精确有效的方法。

4 参数研究

由前述的研究可以看出，对于以上讨论的圆柱壳模型，裂纹引起的圆柱壳固有频率改变量相对较小，因此，以下讨论一个壳长比相对较小，壳厚比相对较大的圆柱壳模型(仍满足薄壳理论应用条件)。壳体的几何和材料参数，如表5所示。

算例中流体密度ρf=1 000 kg/m3，流体声速Cf=1 500 m/s，裂纹相对位置和相对深度分别为c=0.3，a/h=0.6。两端固支和两端简支边界条件下充液圆柱壳固有频率结果，分别如表6和表7所示。对应(1,4)阶模态沿轴向三个方向上的模态振型，分别如图2和图3所示。

表5 圆柱壳参数

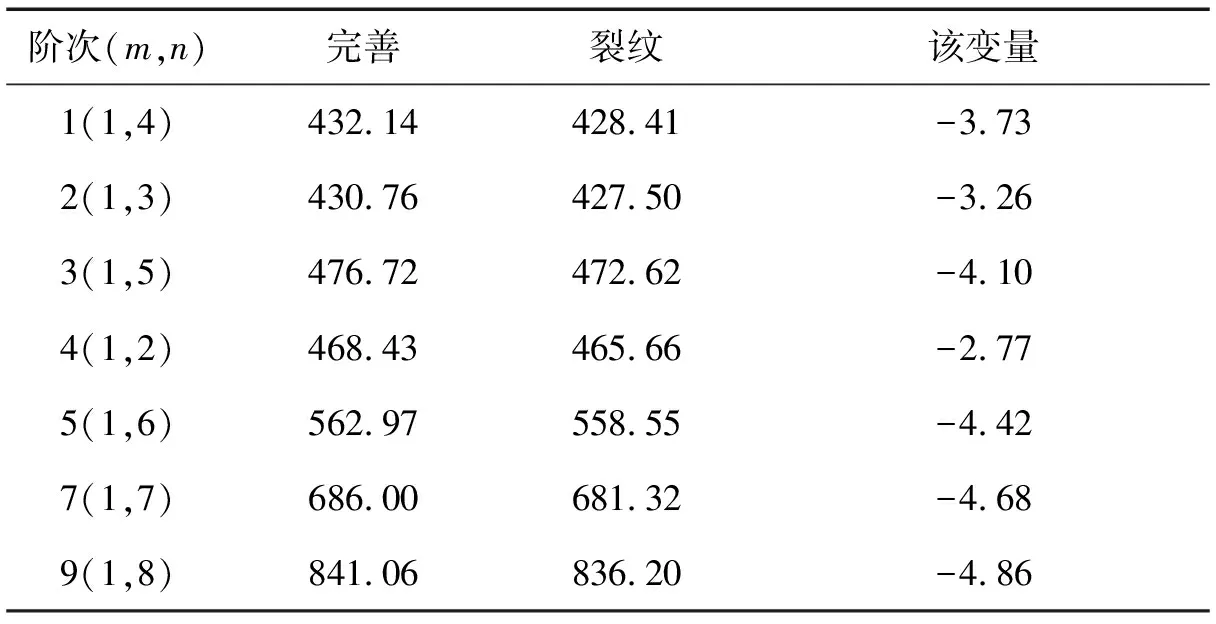
表6 裂纹充液圆柱壳的固有频率(两端固支)

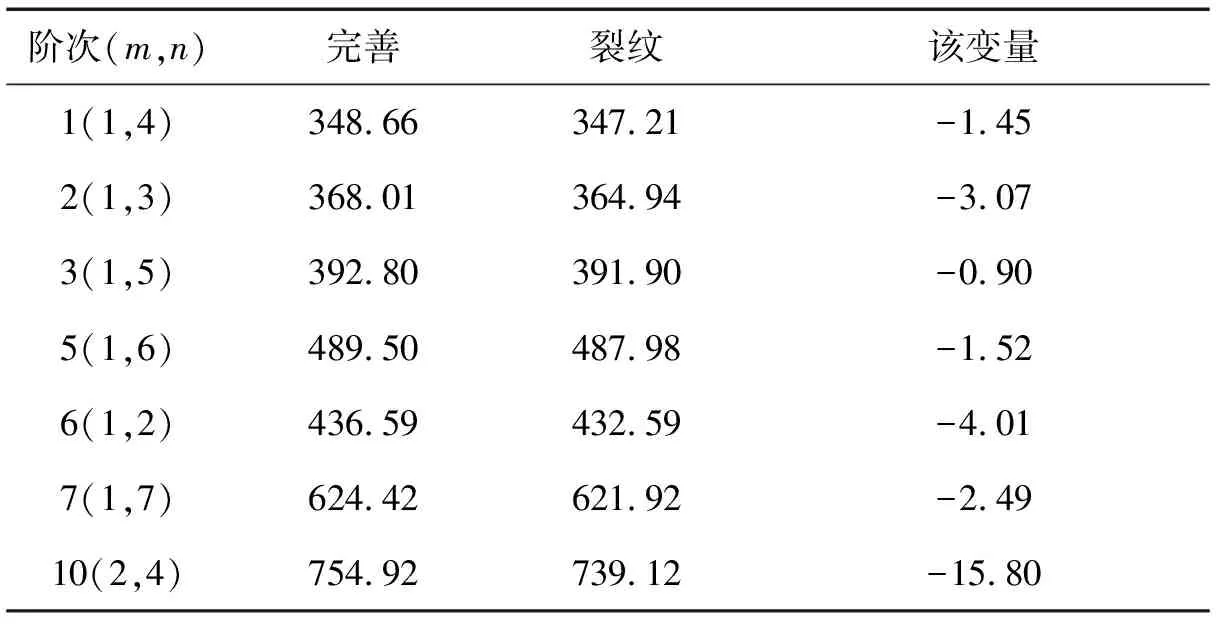
表7 裂纹充液圆柱壳的固有频率(两端简支)

由以上结果可知，对于低阶模态，两端固支边界条件下裂纹引起的固有频率减小大约为4 Hz，整体上两种边界条件下都表现出固有频率改变量随模态阶次提高而增大的趋势。这是由于阶次较高的模态表现出更加明显的局部振动，局部位置存在的裂纹能引起更加明显的振动特性改变。两端固支边界条件下裂纹引起模态振型的改变主要表现为裂纹位置壳体轴向位移上的突变，而两端简支边界情况则主要表现为靠近裂纹端壳体轴向位移幅值的改变。

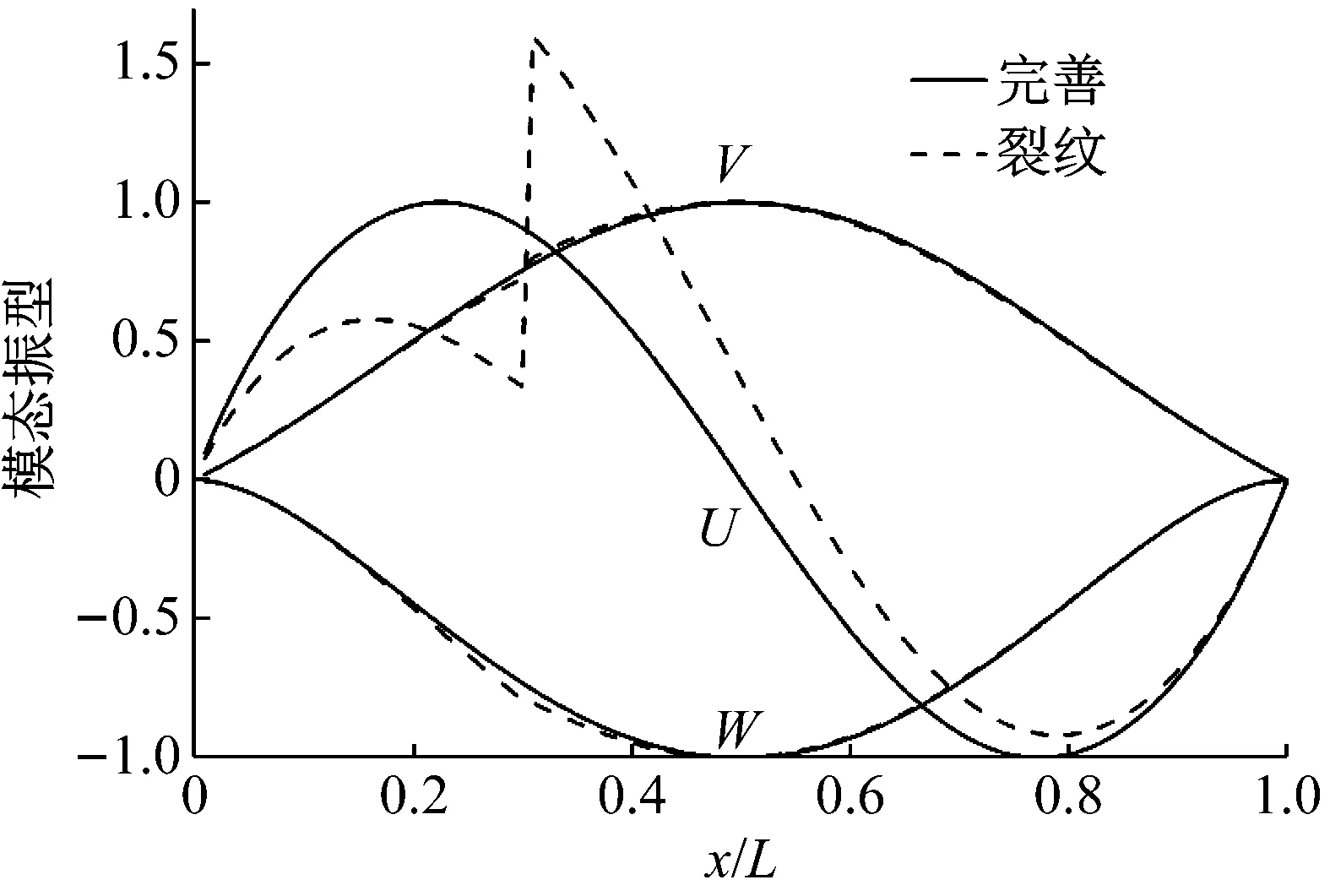
图2 (1,4)阶模态振型(两端固支)

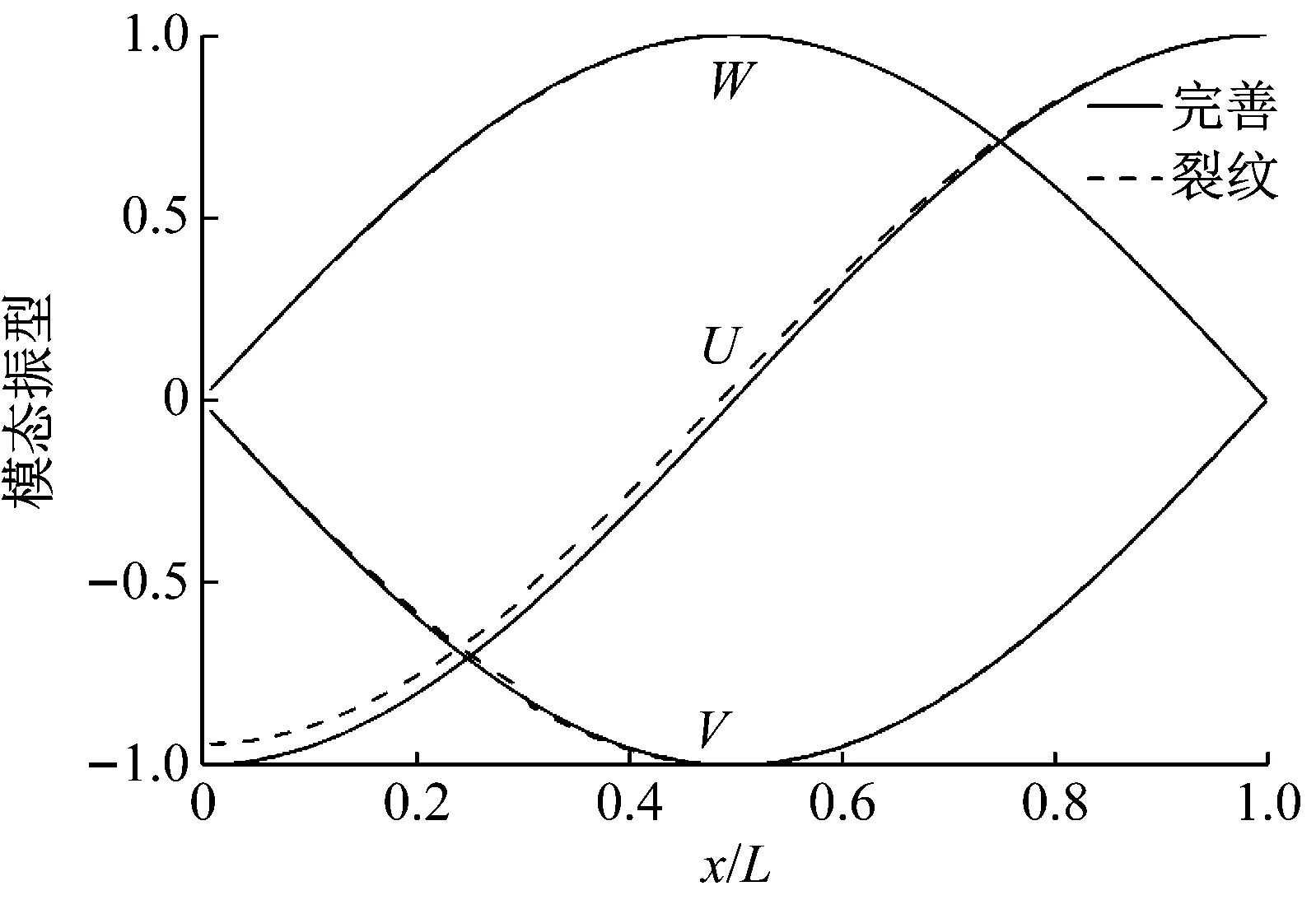
图3 (1,4)阶模态振型(两端简支)

进一步研究裂纹深度和裂纹位置改变对充液圆柱壳固有频率的影响。对于(1,4)阶模态，不同裂纹深度下两端固支和两端简支固有频率结果，分别如图4和图5所示，裂纹相对位置改变的影响，如图6和图7所示。

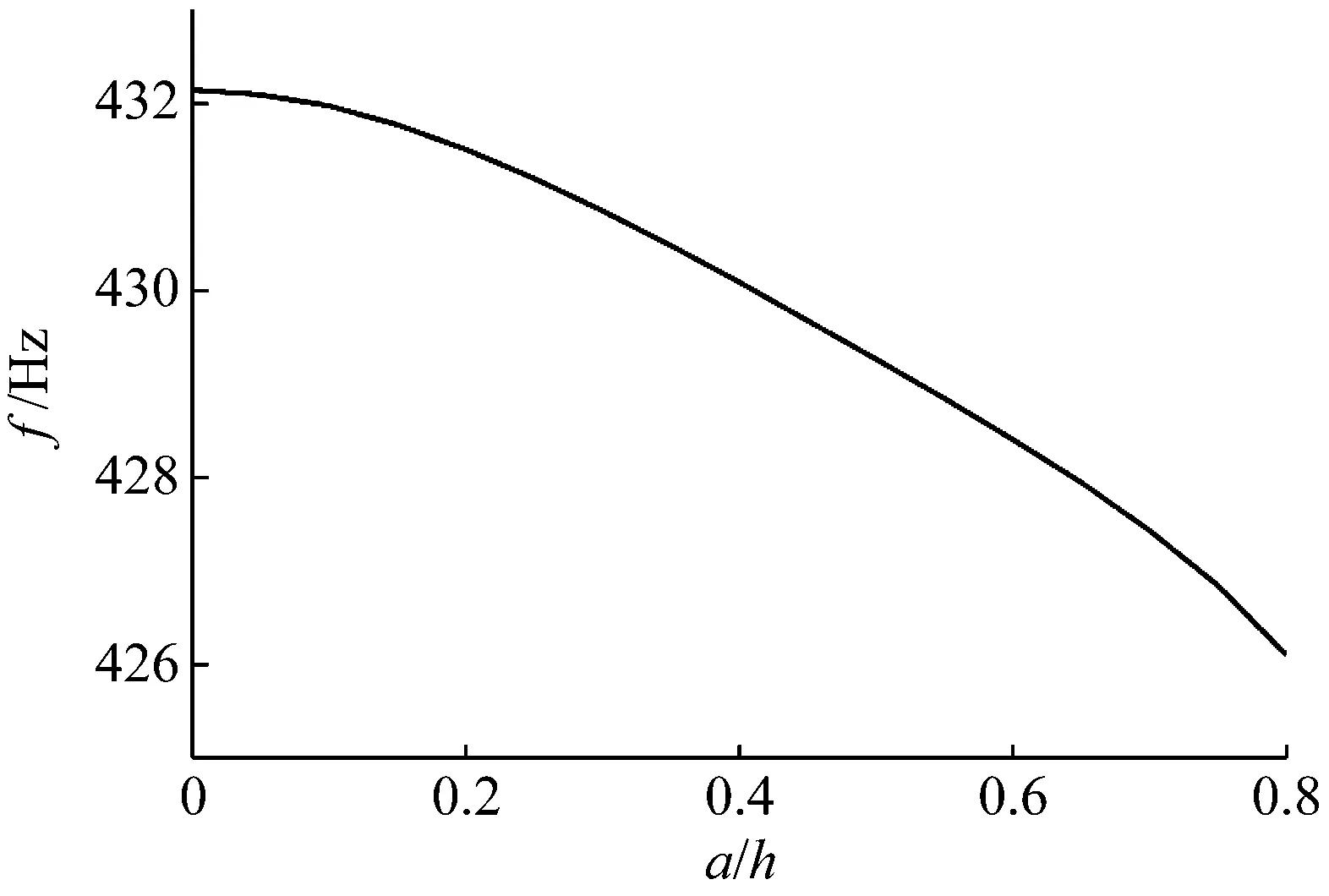
图4 裂纹深度改变对(1,4)阶固有频率的影响(两端固支)

Fig.4 Natural frequencies of the (1,4) mode for different depths of the crack (C-C)

由以上结果可知，随着裂纹深度的增加，充液圆柱壳的固有频率逐渐减小。这是由于裂纹深度增大导致了圆柱壳整体柔度的增加。由图6和图7结果可知，当裂纹的位置更加接近圆柱壳的支撑端时，固有频率减小更加明显。这是由于对于该阶模态，在上述位置壳体中的内力整体较大，裂纹引起的附加广义位移更加明显，即裂纹靠近支撑边界时，裂纹对充液圆柱壳的低阶固有频率影响更显著。

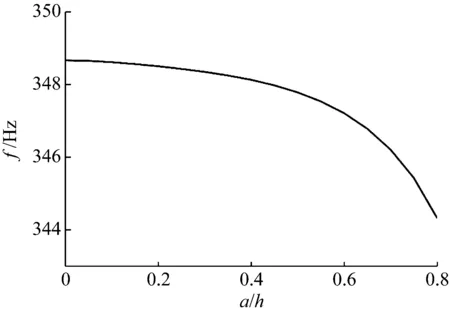
图5 裂纹深度改变对(1,4)阶固有频率的影响(两端简支)

Fig.5 Natural frequencies of the (1,4) mode for different depths of the crack (SS-SS)

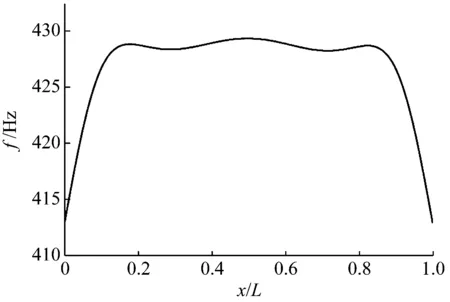
图6 裂纹位置改变对(1,4)阶固有频率的影响(两端固支)

Fig.6 Natural frequencies of the (1,4) mode for different locations of the crack (C-C)

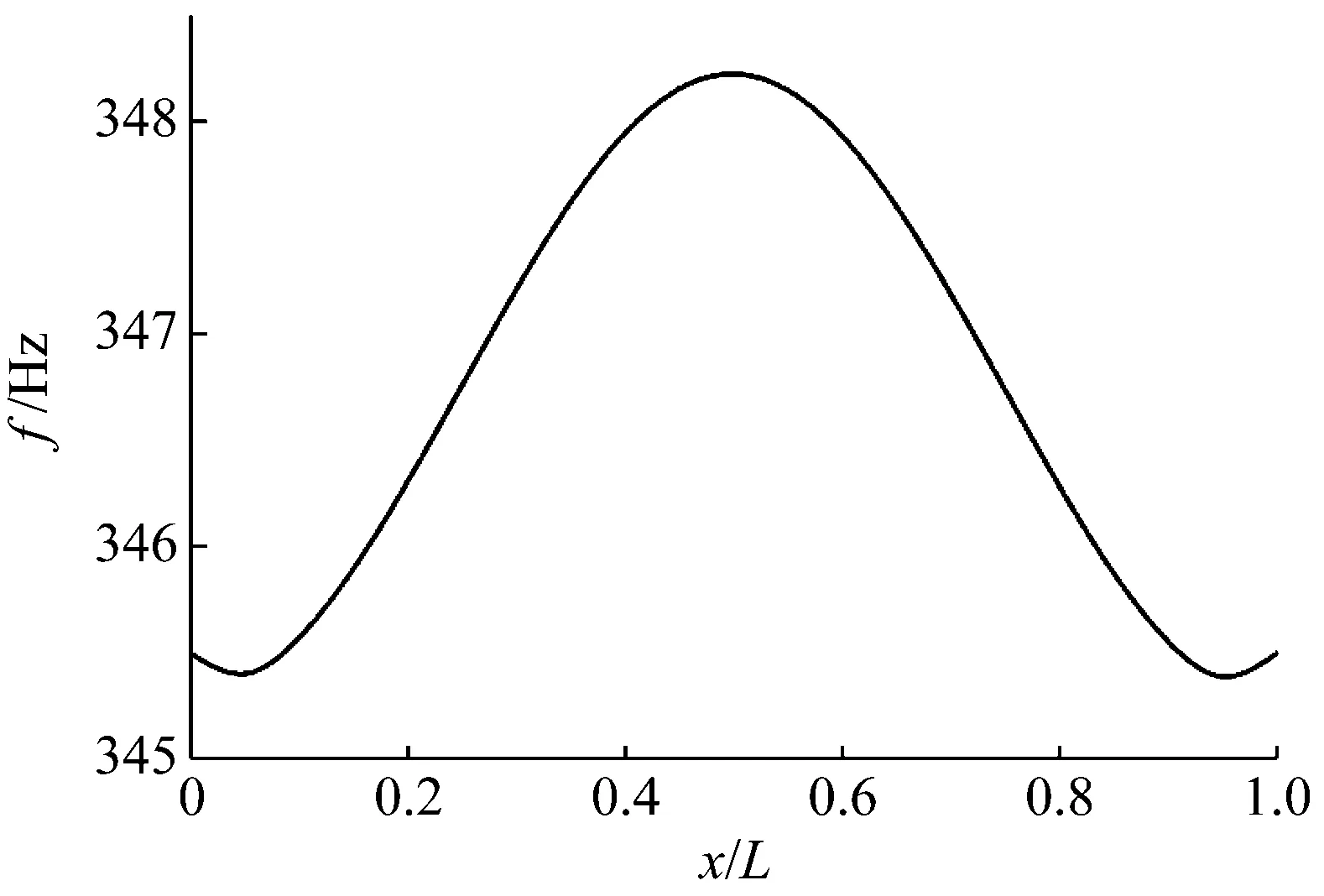
图7 裂纹位置改变对(1,4)阶固有频率的影响(两端简支)

Fig.7 Natural frequencies of the (1,4) mode for different locations of the crack (SS-SS)

5 结 论

本文提出了含环向表面裂纹有限长充液圆柱壳固有频率的理论计算方法。建立了耦合系统的控制方程，通过线弹簧模型来模拟环向裂纹损伤。将本文方法结果与参考文献以及有限元的结果进行对比，验证了本文方法的准确性。通过改变裂纹参数，讨论发现裂纹深度的增加会导致圆柱壳固有频率进一步降低，并且对于两端固支和两端简支边界条件，当裂纹靠近支撑端时，含有裂纹充液圆柱壳固有频率的改变会更敏感。