基于冲击-光纤法的焊接型钢梁损伤检测理论与实验研究
许 颖, 牛 丽, 祖红光
(哈尔滨工业大学 深圳研究生院,广东 深圳 518055)
Ⅰ形钢有横向和纵向两个对称轴,故具有优良的力学性能,被广泛应用于各种工程建筑、桥梁、支架和机械等方面[1]。焊接Ⅰ形钢在翼缘与腹板的连接处受力复杂,这一部位是实际使用中最容易发生疲劳破坏的区域: 某厂平台装机轨道的疲劳破坏实例中,梁上翼缘与腹板连接焊缝全部开裂,梁上轨道因此下沉[2]。
在检测钢结构疲劳损伤[3]方面,传统的无损检测技术存在一些不足: 磁粉和涡流检测只能检测到表面的缺陷[4-5];渗透法只能检测到表面开口的缺陷,并且检测成本较高[6];射线法虽然比较方便,但是对身体伤害很大。近年来出现了很多新兴的无损检测方法[7],但是目前发展还不是很成熟。超声波法是目前使用最广泛的钢结构疲劳损伤检测技术,具有穿透性好、灵敏度高、成本较低、对人体无害等特点。其中冲击回波法是超声检测中常用的一种方法,它利用小锤或者小钢球轻敲结构表面产生低频应力波,应力波在结构体内传播,遇到损伤或结构界面发生反射,反射波被冲击点附近的传感器接收,通过对接收信号的时频域分析可得到结构厚度和损伤位置等信息[8-10]。
本文将能激发宽频信号[11]的冲击回波法和光纤传感器相结合,提出一种冲击-光纤无损检测技术,与压电陶瓷(Piezoelectric Ceramic Transducer, PZT)传感器[12]相比具有以下优点: ①光纤灵敏度相比于其他传感器灵敏度很高[13],检测数量级可以达到纳米,能捕捉到极小的应变变化;②在实际工程中,本文所述方法可以预先将光纤沿梁的长度方向粘贴在钢梁表面,这种检测方法适用于只能接触钢梁一个表面的情况,因为在实际工程中,损伤多发生在梁上翼缘与腹板连接处,而上翼缘连接着桥板,不可直接放置检测设备;③检测过程中冲击荷载只需用力锤敲击梁翼缘表面,具有检测快速、数据处理方便[14]等优点,而传统的脉冲超声法则需要在激励设备和钢梁以及接受设备和钢梁表面之间加耦合剂,操作繁琐且耦合效果不好,经常会导致激励信号太弱而无法有效传递到钢梁。 所以本文所述检测方法较适合土木工程粗放型作业的要求,能克服传统无损检测方法的不足,提高检测效率,便捷快速地检测到疲劳损伤的发生,及时采取补救措施, 从而避免灾难的发生。
1 冲击-光纤检测技术原理
当钢梁内无损伤时,应力波在钢梁上下翼缘表面来回反射,上下两界面均为钢-空气界面,每次反射后其相位都会发生改变。波在梁上下界面发生反射的情况如图1所示,实线表示压缩波,虚线表示拉伸波,冲击荷载产生的原始P波都是压缩波,从图中可以看出,经底面反射到达冲击面的P波都是拉伸波,压缩波在界面上产生向外位移,而拉伸波在界面上产生向内位移。设初始波为P,到达底面的奇次反射波3P,5P,7P是压缩波,到达冲击面的偶次反射波2P,4P,6P是拉伸波。在冲击点和P波经一次反射到达冲击面的波2P传播的距离为两倍梁高2D,经历时间t=2D/Cp,并且随后到达冲击面的波4P,6P为等间隔,因此,P波每次到达冲击面引起的上表面位移呈周期性,t为周期,频率为
(1)
式中:D为梁高;fD为应力波在在Ⅰ形梁上下翼缘表面多次反射的频率;CP为波在钢梁中的传播速度。该公式为冲击回波法检测钢梁损伤的核心。

图1 冲击回波法检测原理图Fig.1 Shock echo method schematic diagram
冲击-光纤检测法是在应力波频谱分析的基础上用光纤干涉仪来检测损伤的方法,冲击荷载使梁内产生应力波,粘贴在构件表面的光纤传感臂接收应力波信号,经信号解调和信号处理技术得到信号频谱,对频谱进行分析确定梁内损伤的位置及尺寸。图2为Ⅰ形钢梁的检测结构示意图。

图2 Ⅰ形钢梁损伤检测结构示意图Fig.2 Schematic of damage detection for steel Ⅰ-beam structure
如图2中a点所示,激励作用在上翼缘中心线位置。如图2中AB所示,干涉仪的传感臂粘贴在Ⅰ形截面梁的上表面用来检测其动应变。当激励不在损伤上方时,应力波在Ⅰ形钢梁上下翼缘表面来回反射,在频谱上产生一个主频fD,当激励在损伤上方时,主要产生两个反射波,一个仍为应力波在梁上下翼缘表面的来回反射,第二个为应力波在梁内损伤处和上翼缘表面间的来回反射,此主频为
(2)
式中:d为上翼缘表面和损伤之间的距离;fd为应力波在上翼缘表面和损伤之间多次反射产生的频率。注意在实验中采集到的信号会受环境干扰,应力波遇到其他界面反射也会对其造成一定的影响,信号的去噪将在3.2进行详细阐述。
在上述力学原理的基础上,损伤的位置可按照以下的方法确定: 计算出超声波在钢梁中的传播速度Cp, 通过式(1)和式(2)得到两种主频fD和fd, 如果在频谱中发现fd处有较大峰值,那么敲击所对应位置即为梁的损伤位置。
2 有限元分析
2.1 有限元模型参数
(1) 单元网格尺寸
网格划分的基本准则是在波的传播方向上,单元网格[15]划分尺寸Δx不低于最小波长的1/20。 根据应力波波长,频率及波速之间的关系,取波速[16]v=CP=5 944 m/s,最终得到单元网格尺寸Δx≤3.96 mm。 在满足ANSYS的应力梯度条件,并且保证计算效率的前提下,最终选取Δx=3.5 mm。网格划分在损伤处局部加密,加密单元网格尺寸取整体模型尺寸的1/4。
(2) 积分时间步长
在用ANSYS软件求解波动问题时,积分步长应满足以下两个条件: ①Δt应小到当波在单元之间传播时足以捕捉到波动效应[17]; ②满足Newmark积分法中对于步长的规定。另一方面,本课题需要将位移时程曲线进行快速傅里叶(FFT)变换得到时域信号,FFT变换后的频域图分辨率与Δt成反比, 如果Δt取得太小,将会导致频域图分辨率太低,影响损伤位置判断精度。
2.2 建立Ⅰ形钢梁三维有限元模型
采用ANSYS有限元分析软件进行数值模拟。钢材密度ρ=7 850 kg/m3,泊松比σ=0.3, 弹性模量E=2.06×1011Pa, 三维Ⅰ形钢梁实体选用八节点Solid185单元。Solid185单元为一次单元,单元质量均匀分配到节点上,适合模拟波的传播。网格划分尺寸为3.5 mm,模型两端简支约束(一端约束UX,UY,UZ,ROTX,另一端约束UX,UZ),模型如图3(a)所示。为了方便实验制作,更为了清晰区分超声在损伤界面反射及在梁上下翼缘表面来回反射的信号,本文采用贯穿式损伤来模拟疲劳损伤。图3(b)为通过布尔运算构造的跨中贯穿式疲劳损伤(疲劳损伤在宽度方向上扩展至贯穿腹板的整个厚度方向[18-19])细部图。疲劳损伤与一般损伤的最大区别在于随着荷载循环次数的增加,疲劳中的损伤存在一个累积的过程。本文为了模拟方便,所以在每个模型中损伤的大小是确定的,通过采用带有不同长度贯穿式损伤的模型来模拟贯穿式损伤在长度方向上的扩展情况。这个贯穿式损伤存在一定局限性,其原因是: ①真实的疲劳损伤不规则;②真实疲劳损伤是动态损伤,从非贯穿式慢慢发展直至变成贯穿式损伤。

图3 Ⅰ形钢梁三维建模和疲劳损伤细部Fig.3 Steel Ⅰ-beam 3D model and fatigue damage detail
2.3 不同截面Ⅰ形钢梁跨中损伤可测性
三维模拟采用在Ⅰ形梁上翼缘直接施加半个周期的正弦冲击来模拟实验中小锤敲击产生的冲击波。采用互相关法求解模型中应力波波速为5 208 m/s。
为了表明冲击-光纤法检测Ⅰ形钢梁翼缘与腹板交接处疲劳损伤的普适性,本节对带有不同个数、长度、和位置损伤的不同截面Ⅰ形钢梁进行损伤检测。数值模拟中选择5根不同型号钢梁进行研究分析,其中1~3号Ⅰ形钢梁模型尺寸与实验相同,梁长1 m,损伤位于Ⅰ形梁腹板与下翼缘交接处。Ⅰ形梁的横截面尺寸参数如表1所示,Ⅰ形钢梁损伤位置、长度和个数汇总如表2所示,单位为mm,损伤厚度均为0.5 mm。

表1 Ⅰ形梁横截面尺寸表Tab.1 Cross-section size of Ⅰ-beam

表2 Ⅰ形钢梁损伤位置及长度汇总表Tab.2 Location and length of damage of steel Ⅰ-beams
1号、2号、3号梁分别在损伤正上方(跨中)和距离损伤正上方中心250 mm处上翼缘表面施加激励荷载,激励形式同本章前文所述;4号和5号梁由于梁高较大,在四分之一跨处,应力波比较容易受边界影响,所以选择在跨中和梁右侧距离跨中150 mm处激励。提取上翼缘表面处沿梁长度方向两节点位移差时程曲线来模拟光纤接收信号,经FFT变换得到各截面尺寸Ⅰ形梁对应的频谱,图4为2号梁检测信号频谱。
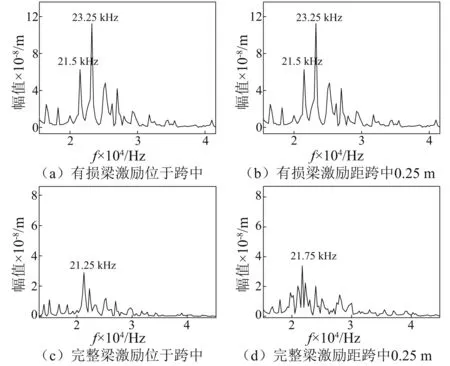
图4 2号Ⅰ形梁(有损及无损)频谱图Fig.4 Frequency spectrum of No.2 Ⅰ-beam with or without mid-span damage
在荷载激励下,不同截面Ⅰ形梁频谱图中对应的主频可由式(1)和式(2)得到理论计算值。钢梁响应所选取的频段可根据理论算出的主频fD和fd来选择。当激励源位于损伤上方时,根据理论计算频谱中将出现21.7 kHz和23.35 kHz两个峰值;当激励源不在损伤上方时,频谱中应仅有21.7 kHz一个峰值。从图4(a)和图4(b)有损梁不同激励位置频谱比较可以看出,当激励源位于有损梁损伤上方时,频谱中出现23.25 kHz和21.5 kHz两个较大峰值,23.25 kHz对应理论中的fd,且23.25 kHz的幅值比21.5 kHz的幅值大很多;当激励源不在损伤上方时,频谱图中只有21.75 kHz一个较大峰值。为了排除激励点位置对检测结果的造成影响的可能性,本文还在完整梁相应位置施加相同激励,得到对应频谱如图4(c)和图4(d)所示。从图4(c)和图4(d)可以看出,在完整梁中激励时,不同激励位置所得到的频谱图的峰值频率只有一个,且数值与fD基本一致,不会随着激励点位置的变化而变化,因此数值模拟结果与理论计算值基本吻合,验证了模型的可靠性,也说明了当激励源在沿梁长方向逐点施加时,可以根据频谱中是否出现峰值较大的fd频率来判断I型梁是否存在损伤以及损伤的位置。
表3为位于跨中长度为100 mm损伤检测结果汇总,可以看出,当损伤长度为100 mm,厚度为0.5 mm时, 5种不同型号的梁均能检测到损伤的存在。

表3 100 mm长跨中损伤模拟结果汇总Tab.3 Mid-span 100 mm damage simulation results
2.4 不同截面Ⅰ形钢梁非跨中损伤可测性
建立损伤位于非跨中处钢梁三维有限元模型,梁尺寸和损伤信息参照表1和表2,分别在损伤正上方(四分之一跨处或者距离跨中0.15 m处)和跨中处梁上翼缘表面施加激励,得到不同截面Ⅰ形梁的频谱,图5为带有100 mm损伤的2号梁检测频谱,从图中可以看出,当激励远离损伤处时频谱中峰值对应的频率为波在梁上下翼缘来回反射形成的主频;当激励位于损伤上方时,得到的频谱中较大峰值所对应的频率比激励不在损伤上方时要大,此峰值就是波在Ⅰ形钢梁上翼缘与损伤处来回反射的主频。将图5和图4对比可知,当损伤位于非跨中位置时,得到的频谱更为复杂。但仍然可以较清晰判断主频的位置。
表4为损伤在梁四分之一跨处或距离跨中0.15 m处不同截面梁的检测结果汇总,可以看出本文提出的检测方法对于损伤位于非跨中处仍然适用。

图5 2号梁损伤位于非跨中处频谱图Fig.5 Frequency spectrum of No.2 Ⅰ-beam with non-mid-span damage

表4 四分之一跨损伤模拟结果汇总Tab.4 Quarter-span damage simulation results
2.5 Ⅰ形钢梁多个损伤的可测性
根据表1和表2建立损伤同时位于跨中和梁四分之一跨(或者距离跨中0.15 m)处的钢梁三维有限元模型。分别在损伤正上方(跨中和右四分之一跨处)以及远离损伤处(距离损伤0.15 m以外)梁上翼缘表面施加激励,得到不同截面梁的频谱图,图6为2号梁存在多个损伤时在不同激励点位置的频谱。
当激励分别位于梁跨中损伤正上方和非跨中损伤正上方时,其结果如图6(a)和图6(b)所示,频谱中会出现两个主频,其中幅值较大的主频对应fd, 能反应损伤的存在和位置信息;当激励远离两个损伤时,其结果如图6(c)所示,频谱中只有一个主频,该主频对应fD, 反应了梁高度信息。本课题分别对1~5号Ⅰ型梁进行了数值模拟,验证了本方法对同时存在多个梁损伤的可测性,由于篇幅有限,此处不再敖述。

图6 2号梁多个损伤频谱图Fig.6 Frequency spectrum of No.2 Ⅰ-beam with multi-damages
2.6 损伤的最小可检测长度数值解
对梁高0.1~0.18 m的有损梁进行损伤检测,损伤长度采用二分法逐渐变小,当损伤位于跨中位置时可以得到如图7所示损伤最小可检测长度随梁高度变化的关系曲线,从图中可见,对梁高0.1 m的Ⅰ型钢梁,理论上可检测到的最小损伤长度为25 mm。图中虚线为模拟数值曲线的线性拟合,从拟合结果来看,损伤最小可检测长度随梁高的增大而逐渐变大,且成一定的线性关系,即梁高越高,能够检测到的最小损伤尺寸越大。对于损伤位于非跨中位置以及多个梁损伤的情况,得到和图7类似的关系曲线。

图7 损伤最小可检测长度随梁高变化关系曲线Fig.7 The relationship curve between the minimum detectable length of damage and the beam height
2.7 损伤测量精度
声场的指向性和扩散性,使损伤长度的测量存在一定的误差。测量精度可定义为损伤可被感应范围(损伤检测长度)与损伤实际长度之差的绝对值。分别对梁高0.1 m和梁高0.14 m的跨中损伤梁进行检测。模型的建立以及检测方法同前文所述,激励点从损伤正中心逐渐向两端移动。由于模型具有对称性,模拟中只研究梁右半跨。表5为损伤测量精度分析表,从模拟结果可知,损伤的测量误差为10 mm左右,是一个绝对值,损伤长度的误差不随梁高和损伤实际长度而变化。

表5 损伤长度的测量精度分析表Tab.5 Accuracy analysis of damage length
3 实验研究
3.1 实验仪器与实验布置
实验中使用力锤敲击梁上翼缘表面中心产生宽频冲击荷载,通过M-Z光纤干涉仪进行信号接收与解调。M-Z光纤干涉仪由分束器构成,当相干光从输入端输入后,输出端的两根基本相同长度的光纤会在汇合处产生干涉,形成干涉场,而干涉场的干涉条纹与输出端的夹角及光程差相关。若固定夹角,则外界条件的改变将直接影响干涉场的干涉条纹并引起光程差即相位差的变化,通过相位差变化可分析出外界因素的变化情况。定义粘贴在钢梁部分光纤传感臂长度为L,则本文中光纤干涉仪所测量的参量为粘贴在钢梁部分光纤长度的变化量ΔL,ΔL与相位差成正比。由文献[14]可知,总相位变化和由超声脉冲引起的应力波所产生的动力应变直接有关。实验示意图如图8所示。被测梁以简支梁形式放置,在腹板/翼缘连接处构造人为损伤,损伤厚度为0.5 mm。跟数值模型一致,疲劳损伤放在下翼缘/腹板连接处,而激励沿着梁的上翼缘表面移动,干涉仪的传感臂通过双面胶粘贴在I 形钢梁的上表面用来检测其动应变。

图8 实验示意图Fig.8 Experiment schematic diagram
根据实验简图连接实验设备,连接后的实物图如图9所示。光纤干涉仪将接收到的信号输入计算机,通过计算机Appl-one软件将信号输出。

图9 实验布置图Fig.9 Experiment layout
3.2 信号采集与处理
光纤传感系统采样频率设为150 kHz,采样时间为5 s。通过光纤传感器对实验室环境噪音进行信号采集,发现采集到的主要为低频信号,其中在49.5 Hz的地方有一个明显的峰值,此频率为实验室的主要噪音频率。由于本文所进行的损伤检测中,我们所关心的频率在10~35 kHz的高频区域,与实验室环境低频噪音差距较大,故可通过对0~100 Hz低频滤波器对实验室环境噪音信号进行信号去噪。
图10(a)为原始信号时域图。对原始信号选取有效时间振动信号后去除低频趋势项,再进行小波滤波,将最终得到的时域图进行FFT变化得到信号频谱。从信号频谱中可以看到两个明显的峰值,如图10(b)所示。
从图10中发现实验频谱曲线中有较多其他频率峰值,不过它们都不在fd频率处,且从图10可见这些频率幅值相对于fD和fd都较小,因此对本文的可测性影响不大;另外,本文检测方法是有参考检测法,即在对损伤位置未知的梁进行检测时,可通过数值模拟或者实验方法获得完整梁的频谱图作为参考。如果被检测梁在某激励点下的频谱图和完整梁基本相同,则认为在此激励点下没有损伤存在;如果被检测梁在某激励点下的频谱图中在频率fd附近出现完整梁频谱图没有的且幅值较大的主频,则可初步认为在此激励点附近存在损伤。

图10 原始信号时域图以及处理后信号频谱图Fig.10 Original time-domain signal and frequency spectrum of processed signal
3.3 不同尺寸Ⅰ形钢梁疲劳损伤检测
实验中采用的Ⅰ形钢尺寸参照表1中1~3号梁尺寸, 损伤的个数、长度及位置如表2所示。
实验时用力锤分别在损伤正上方和远离损伤处敲击,为了能更好地检测到损伤的存在,在损伤处敲击时,将激励加载点选在损伤正上方中心处,远离损伤处激励点应同时满足不受梁两端边界干扰和不受损伤干扰的条件,这里我们选距离损伤0.15~0.25 m同时距离梁两端边界0.2~0.25 m的几个点施加激励。
图11为损伤长50 mm时1~3号梁试件的检测结果频谱图,其结果与数值模拟结果一致,从图中可以看出,当力锤敲击远离损伤时,检测结果频谱中仅出现一个比较大的峰值,此峰值对应的频率为应力波在梁上下翼缘表面来回反射的频率fD,说明在这些位置不存在损伤;当力锤敲击位于损伤正上方时,得到的检测结果频谱中除了fD以外,还会出现另一个更大的峰值,此峰值对应的频率为应力波在梁上翼缘表面与损伤界面之间来回反射的频率fd,此时敲击所对应位置即为损伤位置。
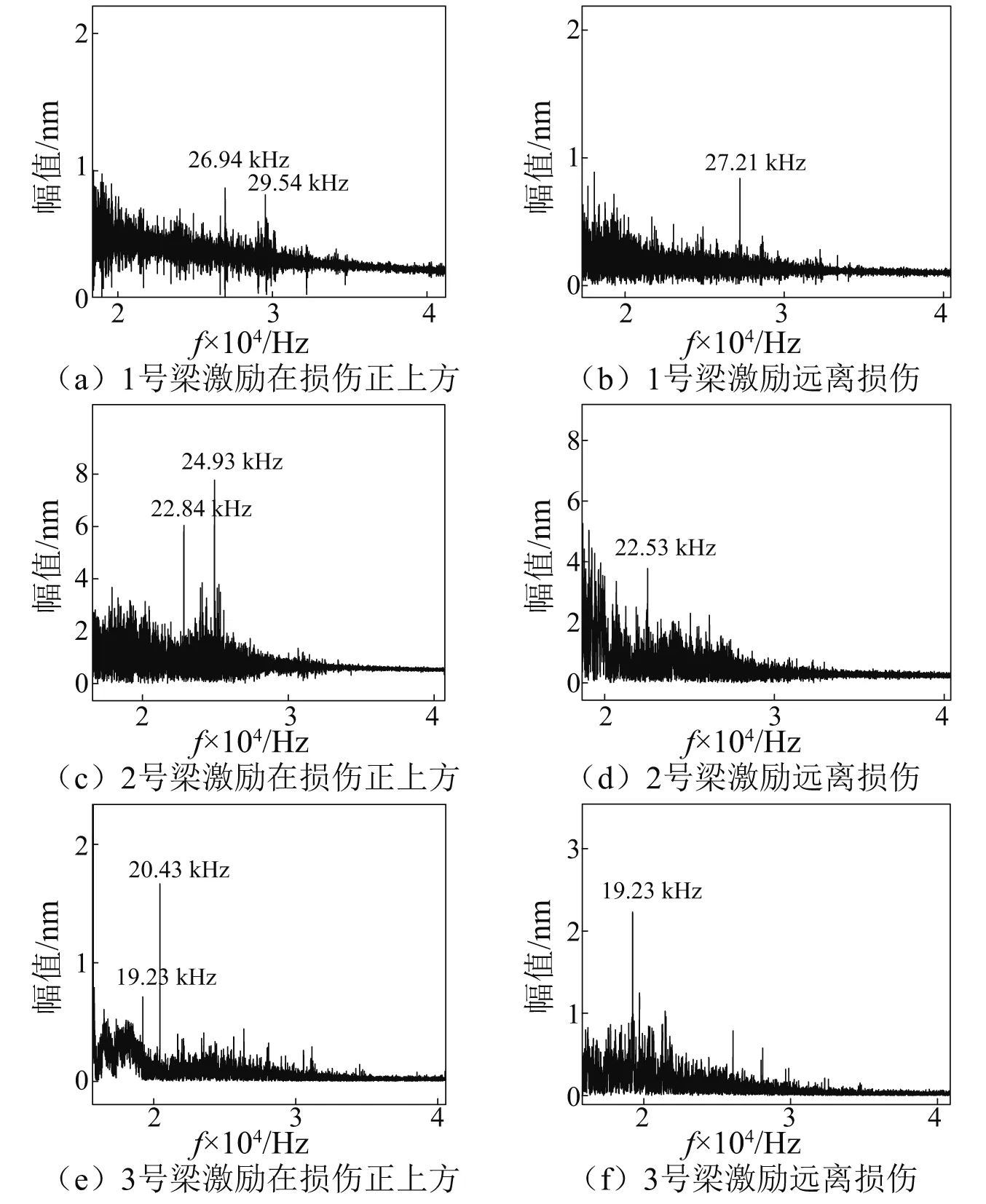
图11 跨中损伤50 mmⅠ形钢梁频谱图Fig.11 Spectrum of 50 mm damage at mid-span of the Ⅰ-beam
表6为位于跨中长度为50 mm损伤时检测结果,可以看出,对于三种不同型号Ⅰ形梁,均能检测到损伤的存在以及位置。但当损伤长度为30 mm时,对于三种不同型号Ⅰ形梁,无论激励施加在损伤上方还是远离损伤处,得到的信号频谱中都只有一个峰值fD,可认为采用本文所述检测方法在实际应用中对长度为30 mm以下的损伤敏感性不足,不能准确找到损伤位置。因此本实验方法对于梁高为1~1.5 m的Ⅰ型梁可检测损伤最小长度为30 mm左右。这个结果和前文中的2.6数值分析结果基本一致。

表6 50 mm长跨中损伤检测结果分析表Tab.6 50 mm mid-span damage detection results
损伤位于四分之一跨位置以及梁内同时存在两处损伤时钢梁的检测结果见表7和表8, 从表7和表8可知这两种情况与损伤位于跨中位置大致相同,可认为采用冲击-光纤法对Ⅰ形钢梁疲劳损伤进行实验检测时,能较准确检测到表2中所列情况损伤的存在以及位置。

表7 50 mm四分之一跨损伤检测结果分析表Tab.7 50 mm 1/4-span damage detection results
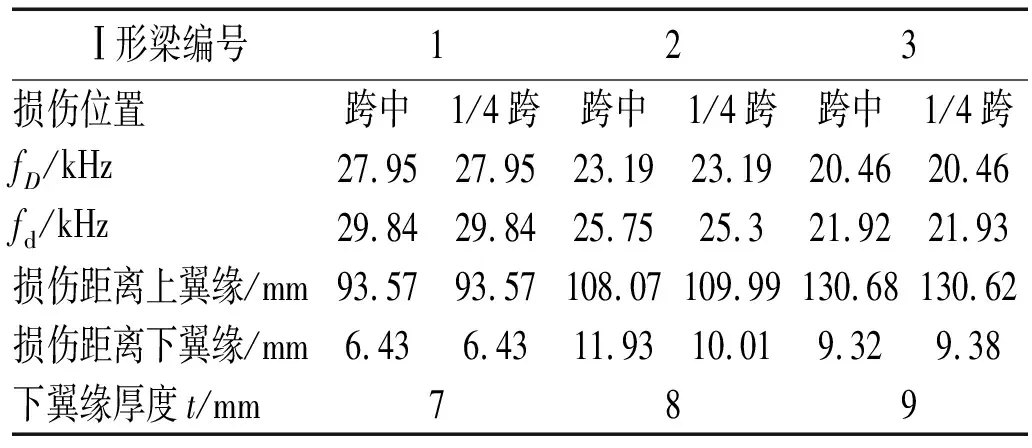
表8 100 mm多个梁损伤检测结果分析表Tab.8 100 mm multi-damage detection results
3.4 光纤粘贴位置对检测的影响
本章前面部分实验均是将光纤粘贴在梁上翼缘表面位置进行损伤检测,实验发现光纤粘贴位置对于检测结果具有一定的影响,本节通过实验来探究光纤粘贴位置对于梁损伤检测结果的影响。这里仅对1~3号三种型号梁长度为100 mm的跨中损伤进行探究,通过信号频谱图来观察当光纤粘贴在腹板不同位置时对损伤可测性影响。光纤粘贴位置如图12所示,分别将光纤粘贴在梁中性轴处的腹板表面以及距离上下翼缘四分之一梁高处腹板表面,用力锤敲击梁上翼缘损伤正上方,经信号采集以及处理后,得到1号梁光纤粘贴在不同位置时实验信号频谱如图13所示。

图12 光纤粘贴位置示意图Fig.12 Fiber position schematic diagram
从图13中可以看出,对于1号梁,当光纤粘贴在腹板3H/4处和腹板H/4处时也能检测到损伤的存在,且频谱图中主频和光纤粘贴在梁上翼缘表面中心处基本相同;当光纤粘贴在腹板H/2处时,得到的信号频谱图中仅有一个峰值,此峰值对应频率为应力波在梁上下翼缘表面来回反射形成的主频,即这种粘贴位置对损伤的存在不敏感。

图13 1号梁光纤粘贴在不同位置时实验信号频谱Fig.13 Frequency spectrum of different optical fiber positions of No.1 beam from experiment
为了验证实验结果的可靠性,通过有限元模型进行了数值分析。图14为通过二维模拟得到的1号梁光纤粘贴在不同位置时数值信号频谱图,从图中可以看出光纤粘贴在梁上翼缘表面、腹板3H/4处和腹板H/4处均能检测到损伤的存在,而当光纤粘贴在腹板H/2时无法通过频谱判断损伤的存在,模拟结果与实验具有一致性,即当光纤粘贴在腹板中部时,本检测方法对损伤的存在不敏感。这可能是因为当光纤粘贴在腹板中部时,光纤的位置接近Ⅰ型钢梁的中性轴位置,中性轴位置既不受拉也不受压,故对应力变化不敏感,因此,在检测条件允许情况下,光纤位置尽可能不要粘贴在腹板中部。

图14 1号梁光纤粘贴在不同位置时数值信号频谱Fig.14 Frequency spectrum of different optical fiber positions of No.1 beam from numerical analysis
4 结 论
(1) 数值模拟和实验研究结果表明,本文所述方法对于不同型号的Ⅰ形梁跨中损伤、非跨中损伤以及梁内多个损伤均具有可测性。当力锤沿梁长敲击在非损伤位置上方时, 在频谱中只有一个主频,此主频对应应力波在梁上下翼缘表面来回反射的频率fD;当力锤沿梁长敲击在损伤位置上方时, 在频谱中除了存在梁上下翼缘表面来回反射的频率fD外,还会增加另外一个主频,此主频对应应力波在梁上翼缘表面与损伤界面之间来回反射的频率fd,通过此时额外增加的主频可判断损伤的存在和位置(长度方向) 。
(2) 数值模拟和实验检测结果表明,本文所述检测方法对于梁高为1~1.5 m的Ⅰ型梁可检测损伤最小长度为30~50 mm左右,且损伤最小可检测长度与梁高大致成线性关系,这一现象无论当损伤位于梁跨中、非跨中还是梁内存在多处损伤时都同样存在;损伤检测长度的绝对误差在10 mm以内。
(3) 通过实验和数值模拟研究了光纤粘贴位置对检测的影响,发现当光纤粘贴在梁上翼缘表面、腹板3H/4处和腹板H/4处均能检测到损伤的存在,而当光纤粘贴在腹板中部时,本检测方法对损伤的存在不敏感。因此,在检测条件允许情况下,光纤位置尽可能不要粘贴在腹板中部。

