考虑颗粒形状的面板堆石坝振动台模型试验DEM模拟

井向阳， 杨利福， 马 刚， 周 伟

(1. 中国电建集团成都勘测设计研究院有限公司，成都 610072； 2. 钦州市水利局，广西 钦州 535000；3. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

粗粒料因取材方便、抗震性能好、施工快捷等优点被大量用于岩土工程中，尤其在超大体积填筑工程中，粗粒料往往被设计者优先考虑为工程主体填筑材料，如碎石桩、铁(公)路路基、建筑基础、堆石坝等。近年来，在我国西南强震区已建、在建或拟建一大批高土石坝(水布垭、天生桥一级、洪家渡、三板溪、糯扎渡、双江口、两河口、如美、马吉等)，其中许多堆石坝坝高达到了200～300 m级，超过现行规范规定的坝高。由于坝高、库大，一旦遭遇超强震而失事，不仅会造成重大经济损失，而且所形成的次生灾害将严重威胁下游人民生命财产安全。因此，有必要对堆石坝动力条件下的力学响应进行深入研究，为堆石坝抗震设计提供参考依据。

汶川地震以来，堆石坝震害引起了国内外学者广泛关注，并开展了大量试验研究。在堆石坝动力响应试验研究方面，杨正权等[1-3]对双江口高心墙堆石坝、两河口高心墙堆石坝和猴子岩高面板堆石坝进行了大型振动台模型试验研究；孔宪京等[4]进行了地震作用下面板堆石坝面板错台振动台模型试验研究，并在土石坝坝坡模型振动台破坏试验基础上，通过数值分析研究了坝坡动力特性[5]；Yuan等[6]制备了心墙堆石坝和面板堆石坝室内缩尺模型，并通过振动台上施加不同动力激励研究了堆石体的动力响应；Torisu等[7]通过大型振动台模型试验和室内剪切试验预测了堆石坝的动力残余变形；徐泽平等[8]采用离心模型试验研究了新疆察汗乌苏砂砾石面板坝在施工期和蓄水期坝体动力响应；程嵩等[9-10]通过动力离心模型试验研究面板堆石坝震动响应及变形规律；Kim等[11]通过动力离心模型试验研究了心墙堆石坝和面板堆石坝的地震响应。堆石坝震害现象观察和振动台动力模型试验表明，堆石坝地震破坏始于下游坡面顶部的堆石体松动、滚落，最终导致坝顶坍塌。

在数值试验研究方面，受计算机处理能力限制，堆石坝动力响应较多采用连续介质理论进行数值分析。刘汉龙等[12]研究了云鹏心墙土石坝的地震易损性；张锐等[13]在研究了土石坝地震加速度动态分布、坝坡抗震能力；Arici等[14-15]在地基振动不同步、不同方向振动荷载对堆石坝动力响应的影响做了大量研究。目前，也有一些学者采用非连续介质力学方法对堆石坝动力响应机制进行研究。孔宪京等[16]结合振动台物理试验，采用非连续变形分析方法(Discontinuous Deformation Analysis,DDA)研究了面板堆石坝地震响应特征及破坏过程；刘汉龙等[17]利用离散元软件PFC2D模拟了土石坝振动台模型试验。

离散单元法(Discrete Element Method, DEM)是研究颗粒系统宏细观力学特性的数值模拟方法之一，其能够从细观角度对颗粒体的各种力学特性进行分析，为研究地震条件下堆石坝动力特性提供了一条有效途径。本文借助有限元网格划分技术，提出了复杂形状颗粒DEM模拟方法，实现了包括了凹多边形在内的不规则随机多边形颗粒模拟；考虑堆石体颗粒复杂形状，模拟了堆石坝模型振动台试验，研究了地震峰值加速度对面板堆石坝动力响应的影响，并揭示了堆石坝细观动力特性。

1 复杂形状颗粒DEM模拟

在有限元-离散元耦合分析方法(Combined Finite-Discrete Element Method, FDEM)中，可以采用随机多边形(或多面体)来模拟颗粒形状[18-19]，然而，当颗粒形状拓扑结构比较复杂(如凹多边形)时，FDEM接触检索方法将无法准确识别接触颗粒。在DEM模拟中，颗粒的形状多为二维圆盘或三维圆球，无法考虑颗粒之间的嵌入咬合作用，数值模拟结果与实际颗粒的力学性质存在一定差异。为此，许多学者将形状简单的圆盘或圆球通过一定的方式组合在一起形成“颗粒簇”(cluster)或“超级颗粒”(clump)来反映颗粒的不规则形状[20-21]。此外，在DEM方法中也有以椭圆或者椭球为基本颗粒的，通过改变椭圆的长短轴之比来模拟不同颗粒形状[22]。上述DEM研究只能模拟一些形状简单且规则的颗粒，对于岩土工程中的复杂形状颗粒往往需要借助图像获取技术才能实现真实颗粒形状的再现。Wang等[23-24]采用CT扫描技术获得颗粒表面信息后，在离散元模拟中用“超级颗粒”重构了真实颗粒形状，但CT扫描方法能提供的颗粒形状很有限，无法反映真实岩土颗粒形状的随机性和多样性。

常晓林等[25]在椭球面上随机布点后生成三维凸多面体颗粒，通过改变椭球长短轴之比和颗粒点数来控制颗粒形状。本文提出的随机多边形模拟方式可以生成包括凹多边形在内的复杂颗粒形状。复杂多边形颗粒由边数、极角、圆半径表征确定，如图1所示, 具体生成方法包括六个步骤。

图1 复杂多边形颗粒的表征Fig.1 Characterization of polygon particles

步骤1在指定区域内按照给定级配曲线生成随机圆形颗粒，此时，颗粒圆心位置(x0，y0)和半径r已知。

步骤2指定最大边数和最小边数，生成多边形随机边数。

n=nmin+int[(nmax-nmin)rand]

(1)

式中:n为生成随机多边形的边数；nmin为最小边数； int为取整函数；nmax为最大边数； rand为0～1的随机数。

θk=2π[1+(2rand-1)δ]/n

(2)

(3)

步骤4获取多边形顶点坐标。

考虑到本文数据结果表征的不足，课题下一步的重点是修正生态足迹模型，筛选恰当变量指标，使数据结果更为精确，希期为宁德市经济、社会、生态可持续发展提供科学的理论参考和数据借鉴。

(4)

图2、图3分别为λ=0和λ=0.2时生成的随机多边形。 当λ=0时，所生成的随机多边形为圆内接凸多边形，随着边数的增加，随机多边形的形状越接近圆。 当λ≠0时，本文提出的随机多边形生成方法可以生成凸多边形和凹多边形，当边数较少时，所生成的多边形为凸多边形但与圆无内接关系，随着边数的增加，颗粒形状就越复杂，与岩土工程中的真实颗粒形状越接近。

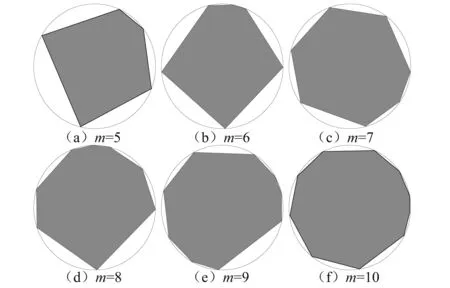
图2 生成的凸随机多边形(λ=0)Fig.2 Polygon particles considering λ=0

图3 生成的复杂随机多边形(λ=0.2)Fig.3 Polygon particles considering λ=0.2

步骤5根据以上复杂多边形的边数、极角、圆半径等几何信息，在有限元软件ANSYS中生成多边形面，并对各个面进行网格划分。

步骤6通过在有限元软件ANSYS中获取的网格形心位置及网格面积等信息，在离散元软件PFC2D中用等面积同形心圆盘替换各个网格，并将同一多边形内的圆盘采用clump命令组构成为“超级颗粒”，以此模拟复杂随机多边形，如图4所示。在PFC2D中clump作为一个独立的刚体参与计算，clump内部的颗粒重叠将会被忽略。

图4 有限元网格与DEM计算颗粒Fig.4 Finite element meshes and DEM clumps

2 堆石坝振动台试验DEM模拟

2.1 计算模型与参数

模型坝体断面为梯形，如图5所示，模型坝坝高取为0.6 m，上游水位0.55 m，上下游边坡均为1∶1.4，坝顶宽0.08 m，面板厚度6 mm，坝体采用粒径0.008～0.024 m的均匀级配，初始孔隙率设定为0.15。

图5 振动台试验DEM模型Fig.5 Discrete element model of shaking table model test

在振动过程中颗粒间的相互作用会消耗部分能量，为了模拟系统中能量的耗散，本文引入黏滞阻尼与局部阻尼作为耗能机制，局部阻尼系数取0.1，法向和切向黏滞阻尼系数均取为0.2[26]。数值模拟中涉及到的参数有: 颗粒密度取为2 650 kg/m3，颗粒间摩擦因数取0.5，多边形颗粒间的接触采用修正的线性接触模型，即kn=k0×r，kn为法向接触刚度，r为多边形颗粒等效半径，k0取1×105kN/m2， 切向刚度ks=kn。 采用汶川波作为输入地震荷载，见图6。为了减小颗粒振动分离对数值模拟的影响，所施加的地震荷载为水平方向，振动持续15 s，并设置了峰值加速度不同的三组输入地震荷载作为对比试验，分别为0.12g，0.26g和0.445g。通过时间积分，得到不同峰值加速度下的速度曲线，将经过基线校正的速度曲线作为坝体底部墙体的水平运动速度。

图6 汶川地震加速度记录曲线Fig.6 Acceleration of Wenchuan earthquake time history

2.2 结果分析

图7和图8 所示为不同峰值加速度下面板堆石坝震后变形模拟结果。由图可知，当峰值加速度为0.12g时，下游坝坡表层颗粒近乎平行原坝坡面滑动；随着峰值加速度的增大，下游坝坡颗粒滑移面角度变大，坝坡坍塌明显，这与文献[27]一致。受面板约束和上游水压力作用影响，上游坝坡位移较小，但面板与底板出现了滑动，最大位移出现在坡脚附近，表明面板止水部位在地震作用下容易受损。在竖直方向上，不同加速度下坝体内部颗粒均出现了向下位移，且随着加速度的增大，颗粒沉降越明显。

图7 震后堆石坝水平向变形Fig.7 Horizontal displacement of CFRD after the earthquake

图8 震后堆石坝竖直向变形Fig.8 Vertical displacement of CFRD after the earthquake

由地震前后坝体轮廓变化可见，地震导致了坝顶的坍塌和上下游坝坡向外鼓出，为了定量比较峰值加速度对坝体变形的响，统计了不同峰值加速度下面板堆石坝模型震后轮廓特性，如图9。震前，上下游坝坡斜率均为0.714 3，震后上下游坡脚向外扩张，坝坡斜率减小，且下游坝坡比上游坝坡更缓，随着峰值加速度的增加，下游坝坡斜率从0.623 9变为0.556 9，坝顶高程从0.559 2 m减小为0.537 8 m。在0.12g峰值加速度汶川波作用坝体断面面积从0.552 m2最大增大到了

图9 震后堆石坝轮廓线Fig.9 Skeleton for CFRD after the earthquake

0.567 2 m2，峰值加速度越大，坝体剪胀越明显。模拟结果与紫平铺面板坝汶川地震后实际变形不一致[28]，但与室内振动台模型试验一致。这主要是堆石体在低围压下剪胀变形而高围压下颗粒破碎抑制剪胀，振动台试验未考虑堆石体颗粒破碎效应，模拟结果(包括物理试验和数值试验)与高堆石坝震后变形不一致。

图10为不同峰值面板堆石坝震后力链分布图。图中接触力大于平均力且被接触力较小颗粒围绕的柱状结构颗粒体系的接触被定义为强力链[29-30]。由图可知，坝体蓄水后强力链基本呈对称分布。地震过程中，静力平衡下的强力链开始崩塌，并伴有新的强力链形成。震后坝体强力链总体分布向下游倾斜。

颗粒材料堆积特性与其细观组构密切相关。Rothenburg等[31]采用傅里叶函数来拟合强力链法向接触力的角域分布，其表达式为

fn(θ)=f0[1+ancos 2(θ-θa)]

(5)

式中:f0为颗粒法向接触力平均值；θ为颗粒接触法向与试样水平面的夹角；θa分别为法向接触力各向异性

图10 震后堆石坝力链分布图Fig.10 Force chain distribution of CFRD after the earthquake

的主方向；an为反映法向接触力各向异性程度的傅里叶系数。

图11给出了不同峰值加速度下堆石颗粒间接触法向力各向异性分布图和相应的傅里叶函数拟合结果。图中每6°一个区间，统计接触法向落入角度区间内的强力链平均法向接触力。震前，坝体强力链玫瑰图呈“花生状”分布，法向接触力主轴方向接近于竖直方向。震后，坝体强力链玫瑰图呈“椭圆状”分布，法向接触力主轴方向减小，即向下游偏转，与图10结果相似。与震前相比，震后法向接触力各向异性变小，但随着峰值加速度的增大，颗粒间接触法向接触力各向异性程度逐渐增强。

图12为地震过程中面板堆石坝内部强力链数演化图。由图12可知，地震过程中，坝体内部强力链的失效多于新的强力链形成，且随着峰值加速度的增大，强力链失效强度越大。为了研究颗粒接触处的摩擦特性，定义摩擦激励指标Im=|ft|/(fntanφu)，IM为颗粒集合体中所有接触的平均摩擦激励指标，图13为不同峰值加速度下的坝体平均激励指标IM在地震程中的演化过程。地震初期，平均摩擦激励有所减小。随着峰值加速度增加，平均摩擦激励增大，但峰值加速度为0.26g和0.445g时，坝体平均摩擦激励相差很小，在0.62处波动，即在不同地震荷载下，坝体破坏时所激发的平均摩擦激励是一个定值。说明面板堆石坝在相同初始组构条件下抵抗地震破坏的能力是一定的，与加载条件无关。

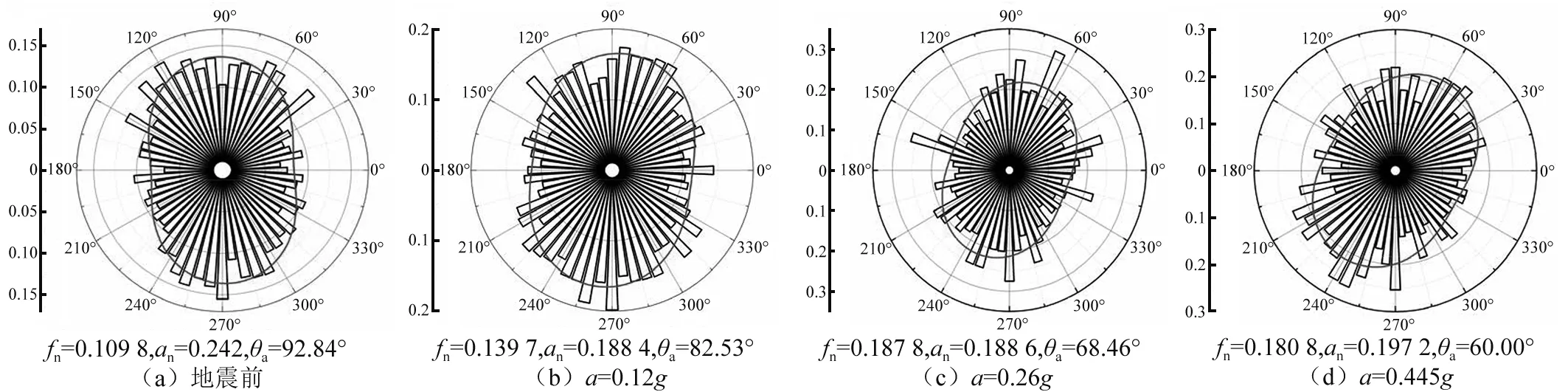
图11 震后堆石坝法向接触力各向异性分布图Fig.11 Normal contact forces anisotropy distribution for CFRD after the earthquake

图12 地震过程中堆石坝内部强力链数Fig.12 Number of strong force chain for CFRD during the earthquake

图13 地震过程中堆石坝摩擦激励演化规律Fig.13 Evolutions of average friction mobilization for CFRD during the earthquake

3 结 论

本文提出了复杂形状颗粒DEM模拟方法，模拟了面板堆石坝振动台模型试验，从细观角度揭示了面板堆石坝动力特性，主要结论如下:

(1) 提出了复杂形状颗粒DEM模拟方法，在PFC2D中实现了包括凹多边形在内的复杂形状颗粒模拟，通过参数控制使得生成的颗粒形状更加真实。

(2) 峰值加速度较小时，下游坝坡表层颗粒沿原坝坡面方向滑动；随着峰值加速度的增大，下游坝坡颗粒滑移面角度变大，坝坡坍塌明显。面板与底板出现了滑动。不考虑颗粒破碎时，地震导致上下游坡脚向外扩张，坝顶沉降，但坝体剪胀。

(3) 震前坝体强力链玫瑰图呈“花生状”分布，法向接触力主轴方向接近于竖直方向。震后，坝体强力链玫瑰图呈“椭圆状”分布，法向接触力主轴方向向下游偏转。随着峰值加速度的增大，颗粒间接触法向接触力各向异性程度逐渐增强。

(4) 地震过程中平均摩擦激励先减小后增大到一个稳定水平。随着峰值加速度增加，平均摩擦激励增大，但在较高加速度下，坝体最大平均摩擦激变化不大，说明堆石坝在相同初始组构条件下抵抗地震破坏的能力是一定的，与加载条件无关。