基于ARIMA模型对广东省生猪价格的短期预测

黄文玲，郑晓颖，Breda McCarthy，张大斌

（1.华南农业大学 数学与信息学院，广东广州 510642；2.詹姆斯•库克大学商业、法律与管理学院，澳大利亚汤斯维尔 4810）

生猪是我国主要的大宗交易农产品之一，也是我国居民主要的生活必需品。据国家统计年鉴数据显示，2013—2016年我国人均猪肉消费量占家庭人均肉类消费量的70%以上[1]。近年来，我国生猪价格周期性波动幅度比较大。自2000 年以来，我国生猪价格大致经历了4 个波幅较大的波动周期，某些地区波幅最高达到80%左右，不仅给生产者和消费者造成了利益损失，而且严重影响到整个农村经济的发展[2-3]。李骥泽等[4]认为，对未来价格周期波动趋势研究不足，不能及时指导生猪养殖户合理调整养殖结构致使养猪跟风，助推了猪肉价格波幅上升。因此，提前预测生猪价格对调控生猪市场供需关系、稳定猪肉价格有着非常重要的意义。

近年来，许多学者展开了生猪价格预测研究，分别用回归分析法[5]、时间序列分析法[6]、人工神经网络模型[7]、结构方程模型[8]、灰系统预测模型[9]以及以上模型的组合[10-11]等定量分析方法刻画生猪价格的波动趋势 ，为更深入探讨生猪价格的波动提供了理论与方法支持。本文将采用ARIMA时间序列分析方法对广东省生猪价格进行短期预测。

1 时间序列与ARIMA模型

时间序列分析与预测已经发展成为一种成熟的价格分析与预测方法，其中，ARIMA模型是时间序列分析与预测常用的方法之一[12]。ARIMA模型是1976年由G.E. P. Box和G. M. Jenkins提出的著名的时间序列方法，用于进行时间序列预测方面的研究，并被改进衍生出了诸多精度优良的模型。ARIMA的基本思想是用一定的数学模型近似地描述和识别预测对象的时间序列，以达到根据历史观测值来预测该序列未来值的目的。

大量学者运用ARIMA模型进行农产品价格预测研究，并获得了良好的预测效果。史冠宇等[13]运用ARIMA模型对青岛市大蒜价格进行了预测，发现了大蒜价格在短期内有持续上涨的趋势；傅如南等[14]运用ARIMA模型对肉鸡价格进行预测，显示肉鸡价格变化明显呈 AR(3)模型规律；罗创国等[15]运用ARIMA模型短期预测中国生猪价格，结果表明，ARIMA模型对生猪价格预测的精度较高，其能准确地预见生猪价格短期波动趋势。以上研究表明，ARIMA模型对农产品价格的短期预测是可行的。

1.1 ARIMA模型结构 在ARIMA模型中，最常用的是差分自回归移动平均模型ARIMA（p，d，q）。该模型中，AR是自回归过程，参数p是其自回归项项数；MA是移动平均过程，参数q是其移动平均项数；参数d表示对研究对象的时间序列平稳化达到平稳状态时的差分次数。

ARIMA（p，d，q）模型的结构[16]：

1.2 ARIMA模型建模流程 ARIMA模型的建模流程见图1。

图1 ARIMA模型建模流程

1）获得观察序列。根据构造的时序图可以初步判定时间序列的平稳性。

2）构造检验统计量。通过构建该时间序列的自相关函数、偏相关函数、单位根等检验统计量来具体检验该时间序列的方差、趋势、季节性变化规律。识别该时间序列是平稳时间序列还是非平稳时间序列。一般情况下，价格、产量、消费指数等时间序列都是非平稳序列[17]。

3）将非平稳时间序列平稳化。如果研究对象为非平稳时间序列，且具有增长或者下降的波动趋势，可进行差分处理来使序列达到平稳状态。如果序列存在异方差，就需要做一定的技术处理，使自相关函数值和偏相关函数值无显著地异于零。

4）基于模型的识别规则来为平稳化后的时间序列建立初步的模型。平稳化后序列的偏相关函数截尾、自相关函数拖尾，则判定可建立AR模型；偏相关函数拖尾、自相关函数截尾，则判定可建立MA模型；当偏相关函数和自相关函数均为拖尾，则判定可建立ARIMA模型。

5）估计模型的参数，对模型进行定阶，并检验具体的模型的可行性。只有可行的模型才具有统计意义。

6）进行假设检验，判定残差序列是否为白噪声序列。

7）经过检验后，用确定好的参数来进行具体的建模，并用该模型来为时间序列进行预测和分析。

2 构建生猪价格预测模型

2.1 数据来源与预处理 本研究原始数据取自“中国猪业网”（http://www.chinapig.cn/）的每日全国生猪价格日报（外三元），选取2012年1月1日—2017年3月31日的广东省生猪价格的日数据作为初始数据（单位：元/kg），以算数平均法求得每月生猪的平均价格。

2.2 绘制时序图 使用SPSS 19.0软件进行数据分析。将处理后的月均价数据录入到SPSS中，构造广东省生猪月均价的时序图，如图2所示。广东省生猪月均价在一定范围内震荡波动，且波动幅度相对较大。初步判断广东省生猪月均价的时间序列是一个非平稳时间序列。ARIMA模型的建立只能基于平稳的时间序列，若序列不具平稳性，首先要进行序列差分。

图2 广东省生猪月均价时序图

2.3 构造检验统计量 为了进一步确定原序列的平稳性，对原序列进行单位根检验。采用ADF检验方法对单位根进行检验。使用Eviews 9.0对原序列进行ADF检验的结果如表1所示，ADF检验统计值约为-1.52 7，均大于1%、5%、10%检验水平的临界值，接受有单位根的假设，表明原序列为不平稳的时间序列。

表1 原序列单位根检验结果

再对原序列的一阶差分进行ADF检验，结果如表2所示。ADF检验统计值约为-5.096，均小于1%、5%、10%检验水平的临界值，且P值极小，仅为0.0001，严格拒绝有单位根的假设，表明原序列的一阶差分为平稳时间序列。由此，可以确定ARIMA模型中的d取值为1。

表2 原序列一阶差分单位根检验结果

2.4 将时间序列平稳化处理 对广东省生猪月均价进行差分处理，生成月均价1阶差分的时序图、自相关图和偏相关图（图3～5）。从图3可以看出，经过1阶差分后的数据能比较均匀地落在0的两侧，序列基本平稳。

图3 广东省生猪月均价1阶差分时序图

图4显示，自相关函数1阶和12阶后的数值趋向于0，后续数值呈现正弦波振动，即呈拖尾性状态；由于1阶与12阶后数值显著趋近0，参数p数值可尝试取1与2、11与12与13。图5显示，偏自相关函数在3阶迅速向0逼近，后续数值呈现正弦波振动但不均为0，即也呈拖尾性状态，参数q数值可尝试在2、3、4中取值。由于自相关ACF检验和偏自相关PACF检验均呈现拖尾性，可考虑采用ARIMA（p，d，q）进行建模。

图4 月均价1阶差分自相关图

图5 月均价1阶差分偏自相关图

2.5 模型参数估计与显著性检验 对上述p、d、q 3个参数的所有可能取值进行组合，基于广东省生猪2012—2015年的月度数据对2016年的月度数据预测进行建模（为了更方便观察预测值与实际值，这里舍弃了2017年1—3月数据）。根据AIC原则并通过反复测试，在所有参数组合中，ARIMA(11,1,4)的建模效果最佳。ARIMA(11, 1, 4)模型的模型统计量表如表3所示。

在模型统计量表中，R的平方数值达到0.805，Ljung- Box Q统计量和显著性都显著大于0.1，证明该模型的拟合程度较高。

再观察ARIMA（11,1,4）模型的ACF和PACF残差图（图6），模型残差序列的自相关系数和偏自相关系数的绝对值均不超过随机区间的范围，均在95%的置信区间内，且序列平稳，即残差序列为白噪声序列，该模型信息提取充分。因此，可以利用ARIMA（11,1,4）为广东省生猪月均价时间序列进行建模并预测。

表3 ARIMA（11，1，4）模型统计量表

图6 ARIMA（11，1，4）模型ACF残差与PACF残差图

图7 基于ARIMA（11，1，4）模型的预测时序图

3 对广东省生猪价格的短期预测

将采用广东省生猪2012年1月—2015年12月的月度数据来预测2016年的月均价格，预测图形如图7所示，拟合值曲线和观测值曲线整体吻合度较高。进一步观察广东省2016年生猪月均价预测值与实际值对比时序图（图8），可以看出，预测值在走势上整体呈现先升后降最后小幅度回升的走势，与实际值的走势方向相同，只是预测值的峰值稍有滞后。表4将预测值和实际值进行具体的数值对比，预测值与实际值的平均误差为-1.10元，平均的偏离程度为-5.42%，误差率在可接受的范围。

4 结论与分析

图8 广东省2016年生猪月均价预测值与实际值对比图

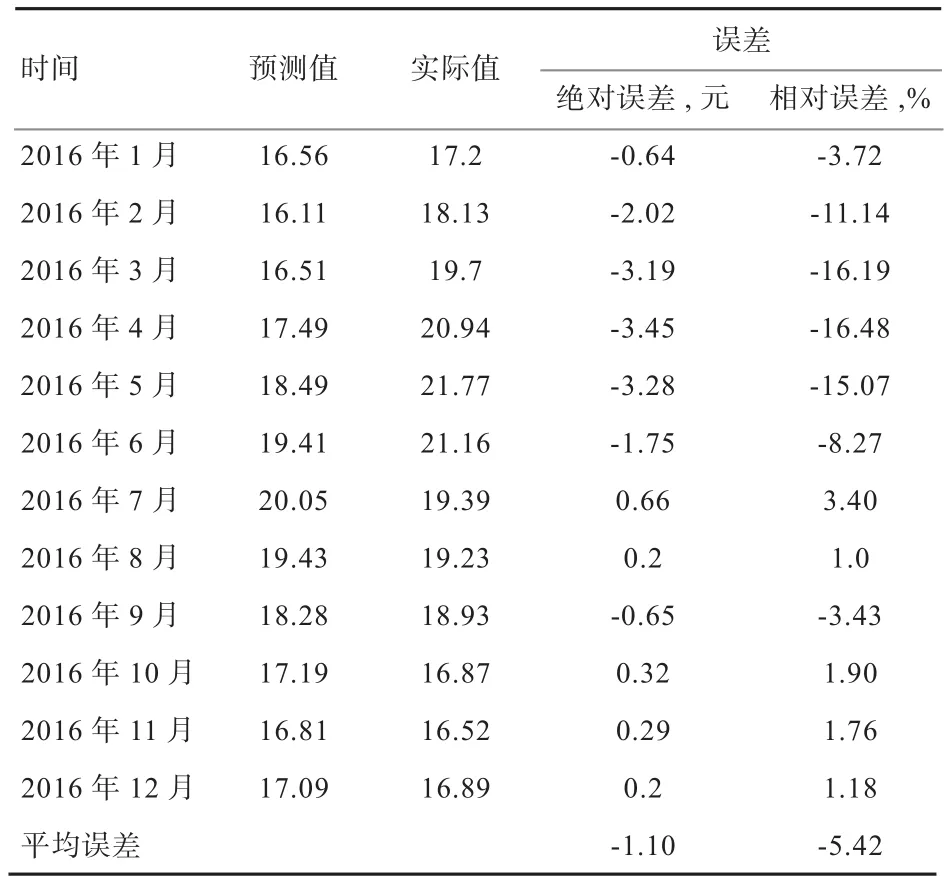
表4 2016年广东省生猪月均价预测值与实际值对比

分析各月份的误差率，发现2016年2—6月误差率较大，其他月份误差率较小。于是，笔者查阅了大量2016年前后关于生猪价格的文献，分析了2016年前6个月我国生猪价格逆势增长的原因。2013 年以来，我国生猪养殖业深度亏损，养猪户资金短缺，大量中小散户退出，加上新《环境保护法》等环保政策影响，南方大批养殖场清退拆除，生猪产能恢复缓慢，整体供给量偏低[18-19]。2016 年初，生猪供给量进一步下降，降至5年来最低水平[20]。同时，由于严寒天气等原因造成国内仔猪死亡率突增，国内生猪供给严重不足，致使生猪价格不断攀升，在6月形成峰值。6月后，由于补栏生猪上市、进口猪肉集中到货，减缓了国内生猪供给不足的状态，加上高价抑制需求、夏季猪肉消费淡季来临等因素，猪肉价格开始回落[21]。综上所述，政策实施、极端天气、价格与供给之间的相互关系等诸多因素的综合作用打破了2016年广东省生猪价格波动的平稳性。

虽然极端的供给关系影响了2016年广东省生猪价格的波动幅度，但是运用ARIMA模型预测2016年广东省生猪的月均价，预测的平均误差率相对较小，预测结果仍然比较可靠。本次实证分析表明，运用ARIMA模型对生猪价格进行短期预测是可行的。