基于微分几何方法的飞翼无人飞行器解耦飞行控制*

屈高敏,李继广

(1 西安航空学院,西安 710077;2 南京航空航天大学,南京 210016)

0 引言

飞翼布局飞机以其良好的气动性能和隐身性能,受到各国的高度关注。许多现代飞机都采用了飞翼布局方式,如美国B-2轰炸机,测试中的美国X-47B、中国的利剑、法国的神经元和欧洲的雷神等。文献[1]指出,有人机/无人机协同作战是可预见未来主要的作战方式之一。无人机舰载机的价值已得到各国的普遍重视,各国正在研制的无人作战飞机几乎都选择了飞翼布局形式。

线性控制理论的一些处理问题的思想为非线性控制理论的发展提供了有益的借鉴。由于直接讨论这些低维子流形比较困难,很多研究者希望把这类问题通过数学方法或数学变换的方式将原问题化为线性问题来研究。这就是非线性系统的线性化思想,在理论上来讲是比较严谨的。

动态逆在无人机[2]、直升机[3]、先进短距起飞/垂直着陆飞机[4]以及大迎角超机动飞机[5]等飞控研究中都得以成功的应用。动态逆方法在求解的过程中计算量很大[6]。在理论上,动态逆方法的时标分离原理也被许多学者所诟病。

自1973年Krener的研究以来[7],学者纷纷关注于在几何可行的条件下,非线性系统的精确线性化问题。近年来,微分几何方法[8]已日益成为非线性系统,尤其是对仿射非线性系统研究中的重要手段之一。

在文献[9]中,基于微分几何理论提出了一种新的非线性动态预测方法。对于强耦合系统的优化问题,文献[10-11]给出了应用微分几何理论的解耦设计方法。文献[12]在研究正则静态线性化问题的基础上,对问题可解性进行了阐述说明。文献[13-14]解决了几类正则动态线性化问题,是通过加积分器实现线性化,并给出几个充分条件得到的。二十世纪以来,多种多样的近似线性化方法,如线性化族[15]、奇异摄动[16-17]、伪线性化[18]、扩展线性化[19]和近似输入-输出线性化[20]等,是为了解决微分几何方法的精确模型而发展的方法。

微分几何方法在飞控中有许多应用。例如,V/STOL[21]巧妙采用近似输入输出线性化,直升机[22]及CTOL飞机的控制设计中采用状态反馈线性化,等等。G.Meyer等人[22]采用12个非线性常微分方程模拟直升机的动态特性,将系统置于三角结构中,对非线性系统进行控制,导出控制系统——Frobenius I型直升机的自动驾驶仪。

虽然基于微分几何理论的精确线性化方法在理论和实践方面取得了一系列成果,但是相对其它方法,该方法的成果依旧较少。在实践方面,主要成果也主要集中在机器人和航天控制领域。造成这种情况的原因有:微分几何理论在物理意义上抽象难懂,不便于工程上的推广;该理论所要求的放射模型很多实际系统不能满足。

文中针对飞翼无人飞行器的耦合特点,对无人飞行器姿态模型适当处理以满足基于微分几何理论的精确线性化方法的要求。从而对飞翼无人飞行器的姿态控制进行了解耦设计。

1 试飞数据分析及研究意义

无人机的飞行耦合现象(如图1)出现在由平飞状态转入滚转状态时,当偏航与俯仰阻尼力矩忽略不计时,侧滑角和迎角是相互等幅转化的。当气流快速变化时,作用在无人机上的力和力矩的波动是不可预知的,会造成无人机的转弯不协同,带来不利的影响。机动性的强弱会影响耦合的效果。

图1 无人机运动耦合

从试飞数据可以看出,无人机转弯过程中存在运动耦合现象,有侧滑角出现,使得无人机航迹的跟踪出现误差。在起飞第一次转弯时,出现了最大1 460.0 m的航迹跟踪误差,如图2、图3所示。由于飞翼无人飞行器独特的气动外形,使其在飞行过程中呈现显著的非线性,呈现出复杂的耦合效应。除前文提到的运动耦合,飞翼无人飞行器的耦合现象还包括:舵面的气动力矩耦合,无人飞行器刚体运动的惯性耦合,气流角交替变化的运动耦合。因此,对飞翼无人飞行器进行解耦设计,对提高无人飞行器的飞行品质具有重要的意义。

图2 无人机的姿态

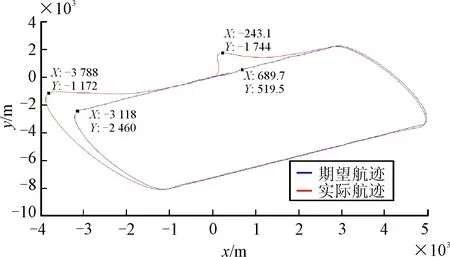
图3 无人机飞行航迹

2 无人飞行器解耦两种常用方法分析

2.1 直接线性化方法与分析

设仿射非线性系统:

(1)

式(1)的直接线性化方法是应用求解微分方程的方式计算求得原系统的一个微分同胚T,使得原系统在坐标变换(式(2))和控制率(式(3))作用下,变换得到线性状态空间的形式(式(4))即:

z=T(x)

(2)

u=φ(x)+ω-1(x)υ

(3)

(4)

假定系统(式(1))经坐标变换(式(2))和控制率(式(3))作用下变换为如下形式:

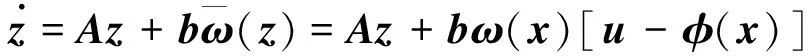
(5)

由式(2)和式(1)可得:

(6)

比较式(5)和式(6)可得:

(7)

式(7)成立的充分必要条件是:

(8)

由此可得:满足式(8)某个φ,ω,A,b和坐标变换z=T(x)时,均能将原系统变换为式(5)的线性空间形式。

在状态空间系数A和b给定的情况下,求解式(8)确定的微分方程组,即可得到φ,ω和T(x)的具体形式。

上述计算过程具有严密的逻辑和近乎完美的结论形式,并且状态空间系数A和b的选取具有一定的自由度,可以满足特殊的设计要求。但是,完美的微分方程形式背后却是求解的困难。在大多时候,这种困难是难以克服的。

以四阶单输入单输出系统,选取A和b可控标准型为例来说明以上求解的困难。

单输入单输出系统可控标准型系数矩阵为:

将以上各式代入式(8)可得:

AcT(x)-bcω(x)φ(x)=

对于以上微分方程可解的系统而言,上述设计步骤是理想的设计方法,但很多系统并不是需要得到可控标准型的单输入单输出系统。即使是可控标准型的单输入单输出系统得到以上微分方程组的解析解也是困难的。根据解析几何学可知,上述方程组在大多数情况下是不存在解析解的。

2.2 无人飞行器姿态方程的一种处理形式与分析

根据力矩定理,无人飞行器受到的力矩可表示为:

(9)

整理后可得到无人飞行器的角动力学方程:

(10)

基于上述以控制力矩(L,M,N)为输入变量的仿射模型进行无人飞行器姿态解耦设计,可以在很大程度上降低设计的难度,并且可以得到令人满意的仿真结果。然而,上述设计思路并不能实现无人飞行器的姿态解耦控制。该设计只是实现了无人飞行器的力矩解耦,但在实际应用中,无人飞行器的各种控制输入都要落实到舵面输入上。根据前文无人飞行器的耦合分析可知,无人飞行器的控制舵面对控制力矩存在强烈的耦合作用,依据该模型设计的结果依然具有强烈的耦合作用。

为了更好的对飞翼无人飞行器进行解耦控制设计,以下将首先建立无人飞行器姿态放射模型。

3 无人飞行器姿态方程的仿射模型

无人飞行器的姿态方程可表示为:

(11)

式中:

从力矩的表示公式可知,无人飞行器的飞行状态产生的力矩只与无人飞行器的飞行状态有关,随飞行状态的改变而改变,将这部分力矩称为状态量。控制舵面产生的力矩不仅与无人飞行器的飞行状态相关,还受到控制舵面的输入的控制,这部分力矩称为控制变量。根据以上划分,无人飞行器姿态方程的仿射模型为:

f(x)=

(12a)

g(x)=

(12b)

4 基于微分几何方法的无人飞行器解耦设计

4.1 微分几何方法的一些结论

仿射型m入m出系统:

(13)

根据文献[7],有以下结论:

定理1:对于系统(式(13)),设矩阵g(x0)的秩为m。状态空间精确线性化问题可解的充要条件是:存在x0的一邻域U和定义在U上的m个实值函数h1(x),…,hm(x),使系统(式(13))在x0有相对阶{r1,…,rm},且r1+…+rm=n。

定理2:对于系统(式(13)),设矩阵g(x0)的秩为m。状态空间精确线性化问题可解的充要条件是:

1)对每个0≤i≤n-1,分布ζi在x0附近有常数维。

2)分布ζn-1的维数为n。

3)对每个0≤i≤n-2,分布ζi是对合的。

在条件中,分布式为:

(14)

定理3:对于系统(式(13)),设矩阵g(x0)的秩为m。存在x0邻域U和定义在U上的m个实值函数λ1(x),…,λm(x),使系统:

(15)

在x0有相对阶{r1,…,rm},且r1+…+rm=n的充要条件是:

1)对每个0≤i≤n-1,分布ζi在x0附近有常数维;

2)分布ζn-1的维数为n;

3)对每个0≤i≤n-2,分布χi是对合的。

定理4:(Frobenius定理)一个非奇异分布完全可积的充要条件是该分布是对合的。

定理5:系统线性化过程,先坐标变换后状态反馈和先状态反馈后坐标变换是等价的。

以上定理是文中推理和计算的依据。其中定理1和定理2给出了系统能够进行反馈线性化的充要条件。定理3给出了构造满足定理1和定理2条件的系统输出的方法。定理4是构造满足可线性化输出函数过程中计算的依据。定理5则可以避免下文解耦计算中一些不必要麻烦。

4.2 标称输出函数的构造

由定理1和定理2知,系统能够实现反馈线性化需要满足以下条件:1)系统的输入输出量在数量上相等;2)系统的相对阶之和等于系统状态个数。以上两个条件很多系统是难以满足的,则在进行反馈线性化之前需要对不满足条件的系统进行相应的处理。

假设系统的输入个数为m,在系统中一些状态量是设计要求的解耦量,这些变量是系统运动状态的直接反映,或者是评判控制器好坏标准量。因此,这些状态量的解耦线性化是系统必须线性化的量。这里把这些必须线性化的量称为解耦输出量。假设这部分状态量的个数为m1。根据上面的条件1),则还应该有m2=m-m1个量作为系统的输出。这部分输出量线性化与否并不是设计工作所关心的。下面论述选取这部分输出的方法步骤。

根据定理2,系统的输出应满足如下条件:

1)正交条件。由相对阶定义,对所有x0附近的x满足:

(16)

此式等价于:

(17a)

(17b)

(17c)

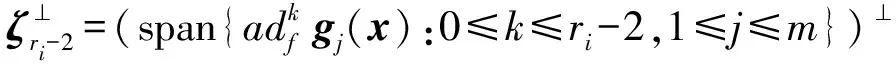
(17d)

2)矩阵非奇异要求。根据相对阶定义,矩阵A(x0)在x0附近非奇异。其中:

3)相对阶总和等于n要求,即r1+…+rm=n。

根据以上条件,来构造标称输出函数。根据定理2,标称输出函数既要独立解耦输出量,又要满足式(17c)。根据定理4可知,标称输出函数是可积的。因此可得标称输出函数。

4.3 仿射模型反馈线性化

经过上面标称输出函数的构造,系统已满足定理1和定理2,所以系统可以精确线性化。系统的线性化步骤如下:

选择定义在x0邻域的坐标变换函数集:

(18)

把系统变换为m组方程:

(19)

式中:

(20)

可解得精确线性化的反馈为

u=A-1(ξ)[-b(ξ)+v]

(21)

经过以上坐标变换和状态反馈,原系统变换为Brunovsky标准形系统:

(22)

经过以上步骤,可将仿射系统变换为标准线性系统。但是,计算的过程并不都是容易的。特别是式(21)中A-1矩阵的求解是很困难的。不过要得到A的表达形式并不困难。根据定理5,A-1的求解并不是必须的。

4.4 无人飞行器姿态方程线性化解耦

观察无人飞行器飞行器姿态仿射模型式(12)可知,无人飞行器的俯仰角受升降舵控制,与其他舵面的耦合较小。所以文中的设计的首要目标是对无人飞行器的偏航角和滚转角进行解耦,同时兼顾俯仰角通道的解耦。

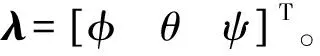
根据式(18),可得系统的坐标变换函数为:

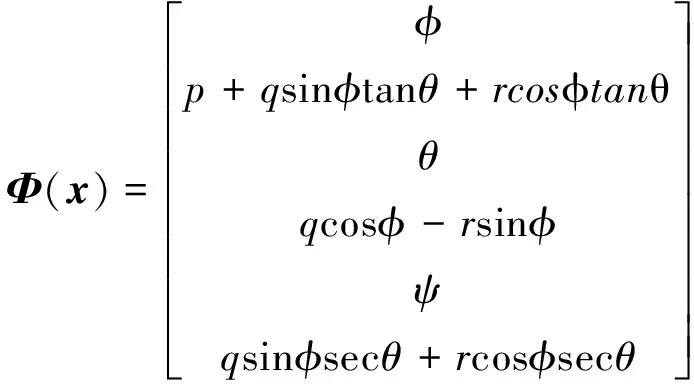
(23)

由式(21)可得:

(24)

(25)

5 无人飞行器航迹跟踪控制

无人飞行器的航迹跟踪包括纵向航迹跟踪和横侧向航迹跟踪两部分。其中,纵向航迹跟踪控制主要有升降舵通道和发动机控制通道。控制器逻辑分别为:

1)升降舵控制

(26)

(27)

(28)

2)发动机控制

(29)

式中：δp 0为不同高度下的配平值,VIASg为当前高度的平飞速度。

横侧向航迹跟踪控制主要包括副翼通道控制和方向舵控制。其中,方向舵通道反馈信号为侧滑角,以实现无人飞行器的协调转弯控制。其控制率结构为:

1)副翼舵通道

(30)

(31)

(32)

式中:φc为滚转角前馈指令，且：

(33)

其中：Yg为预定的航线,ψg为预定航线的航迹角。

2)方向舵通道

(34)

6 控制结果验证

6.1 无人飞行器布局和气动舵面分配

样例飞翼无人飞行器的布局如图4所示。

无人飞行器为无垂尾升力体飞翼布局,气动舵面包括机翼后缘6片舵面和机身上一对阻力式方向舵。

发动机安装在机身中心轴线上,推力方向通过重心。各舵面编号如图5所示。

图4 无人飞行器示意图

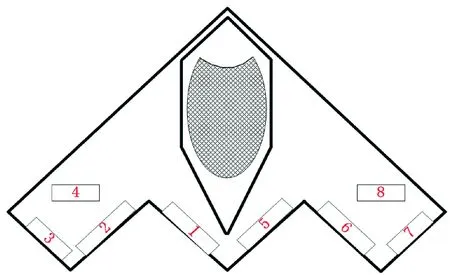
图5 无人飞行器舵面分布

为了减小由于飞翼无人飞行器特定气动特性引起的各舵面间的耦合作用,对无人飞行器8片舵面进行分配组合,使得各组舵面完成不同的控制功能,并在舵面分配时,对每一个控制通道留有一个控制余度。针对样例无人飞行器相对于x轴对称的8片舵面的组合复用分配表如表1所示。

表1 执行器组合复用分配表

在表1中,将无人飞行器的气动舵面分为7种组合方式,对每种组合方式进行如下定义并分析其产生的力矩效应:

1)δ1:1、5号舵面同偏,只产生俯仰力矩;

2)δ2:2、6号舵面同偏,只产生俯仰力矩;

3)δ3:3、7号舵面同偏,只产生俯仰力矩;

4)δ4:3、7号舵面差动,只产生滚转力矩;

5)δ5:2、6号舵面差动,只产生滚转力矩;

6)δ6:4、8号舵面单偏,以阻力方向舵的形式既产生偏航力矩也产生滚转力矩,同时带有一定的俯仰力矩;

7)δ7:3、7号舵面单偏,与δ6作用相同。

当δ2与δ5以及δ3与δ4复用时会带来较小的偏航作用,此处忽略其影响。对于这7种执行器的组合方式,其在整个舵面偏转区间上的操纵效率呈一种非线性的变化规律。

6.2 仿真结果

根据上文空置率,无人飞行器俯仰通道和滚转通道对正弦信号的跟踪如图6、图7所示。

图6 俯仰通道响应

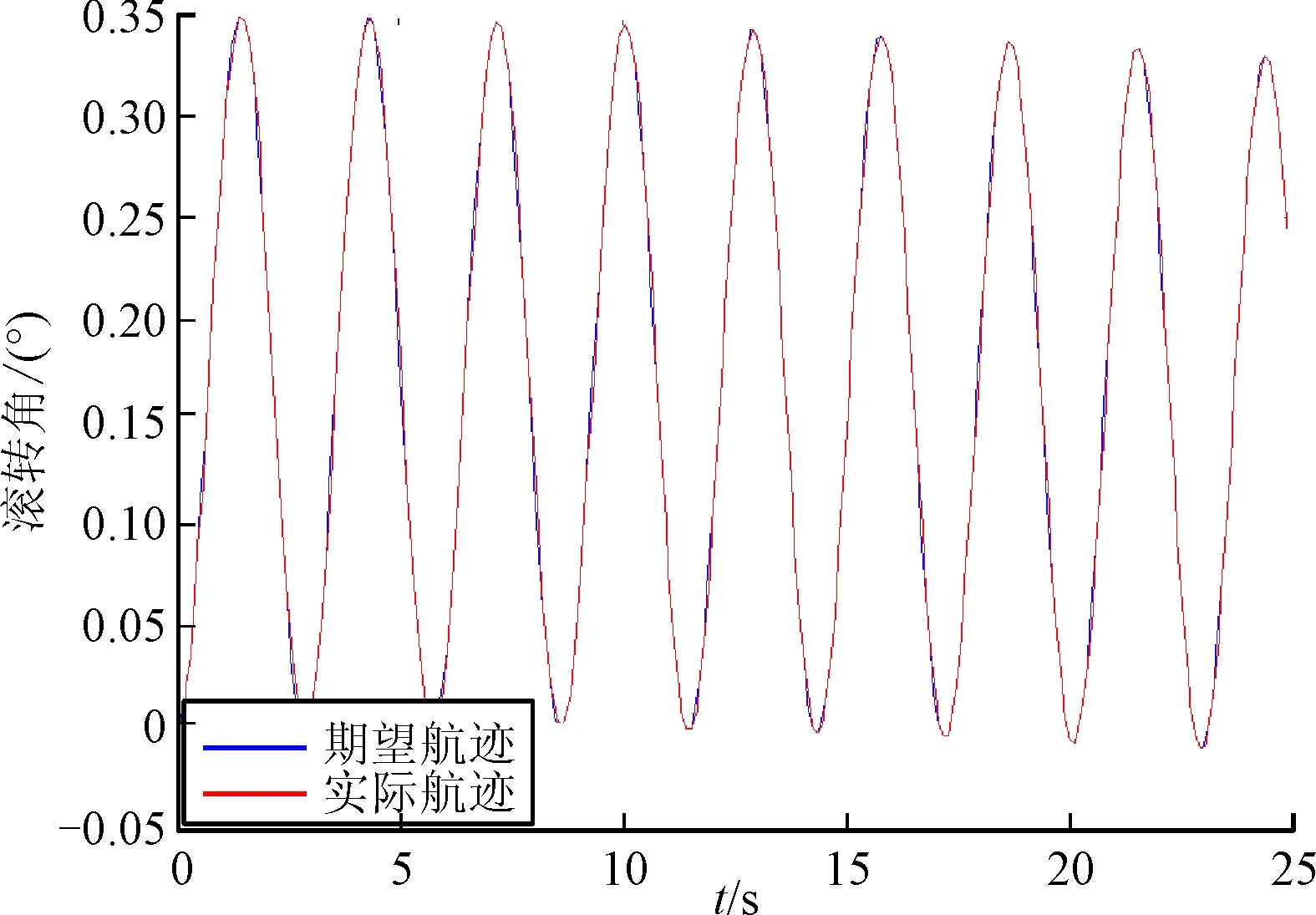
图7 滚转通道响应

无人飞行器对航迹跟踪的仿真结果如图8所示。

图8 无人飞行器航迹

从仿真结果可知,基于微分几何方法可以很好的实现滚转通道和俯仰通道上的解耦,并能快速精确的跟踪指令。

综上所述,基于微分几何方法的飞翼无人飞行器解耦控制是满足工程实践要求的。