深度学习:让学习真正发生
——《三角形的三边关系》一课的教学实践与思考
湖南长沙市长沙县教育研究培训中心 邹旭红
随着“大数据”时代的来临和人工智能与人机交互的大踏步前进,“深度学习”已成为社会生活的重要内容,并被广泛运用到教育教学领域。郑毓信教授在《以“深度教学”落实数学核心素养》一文中,强调学生的数学学习应当成为一种“深度学习”,其核心在于:不应停留于单纯知识(包括数学基础知识和数学基本技能)的学习,而应通过具体知识内容的学习促进自身思维的发展,特别是应当不断提升自身思维的品质,包括由“理性思维”逐步走向“理性精神”。并指出只有教师真正做到了“深度教学”,我们的学生才可能做到“深度学习”,提升核心素养。那么,如何才能有效地促进学生理性地思维,实现“深度学习”呢?下面,以《三角形三边关系》一课为例来谈谈自己的思考。
三角形两边之和大于第三边,这一结论对于四年级的学生来说浅显而直白,没有很高的知识含量。正如曹培英老师说过:三边关系用线段公理直接推理就是,无须证明,这是连动物都知道的事实。实际教学中理想与现实却是背道而驰的,学生对于这样的事实理解是很有难度的。其难点就在于:讨论三角形边的关系是从一个新的视角思考问题,即为什么要把两条边加起来与第三边作比较?如果直接给定一个三角形讲解结论,学生只用5分钟就能理解并能运用结论进行判定,但这样的教学仅仅是“知道”而已,并没有“思维”的价值,如何才能真正驱动学生深入地思考、实现深度学习?选用其中一个教学片段来分析。
一、过程回放;
(一)“围”三角形,直观感受“边”的“长短”影响“三角形”的形成
师:老师这准备长度分别为2厘米、6厘米、9厘米的三根小棒,谁能上来围一个三角形?
(展示台上演示)
生:围成了
生:不行
师:是的,围三角形是有要求的。要像这样,三根小棒要首尾相连才行,这样,三角形三条边的长度才刚好是三根小棒的长度。(边说边用手指黑板)
(二)提出问题,操作探究,感知三角形第三边取值范围
师:那刚刚的三根小棒能不能按这样的要求围成三角形呢?
生:不能。
师:想要把这三根小棒围成三角形,要怎么办?
生:把红色的小棒变长。
师:那固定了6厘米和9厘米,第三条线段在什么范围内就能围成三角形呢?要来研究这个问题,你们有什么好办法吗?
生:找其他小棒试一试。
师:这个主意好!可是老师没有准备那么多红色小棒,只带了这个。(出示直尺)认识吗?
生:直尺
师:没错,谁能带上数学的眼光再看看。
生:上面有线段。
师:你在上面找到了哪些长度的线段?
生1:7厘米、8厘米……
生2:0到20厘米。
师:不同长度的线段找到了,把尺子上跟两根小棒相接的那一段作为第三条线段的长度,(手拿尺子演示)你能想象出围成的三角形吗?真能?那我们来试一个。
展示台上演示:

师:谁上来指指第三条边在哪?围成的三角形又在哪?现在第三条边是几厘米?
生:12厘米。
师:再想象下,将两条边张开得越大,红色小棒就——越长,两边张开得越小,红色小棒就——越短。
师:看样子都明白了。那咱们试试吧,可问题是,我们得试哪些长度呢?
生:3厘米、9厘米……
师:说了这么多长度,怎么没人想试1厘米呢?
生:因为2厘米都围不成,1厘米更围不成。
师:你特别会学习,能从刚刚的学习中寻找经验,了不起!也就是说只要试比——
生:比2大的长度。
出示板贴:

师:为了方便研究,那我们就先从2以上整厘米的长度开始研究。
……
(三)flash动画演示,合情推理,突破难点
师:为了帮助大家理解,老师带来了一个神奇的三角形。这是第三边为12厘米时围成的三角形,如果我拉动这条边,它是会变的哦,想看吗?
生:想。
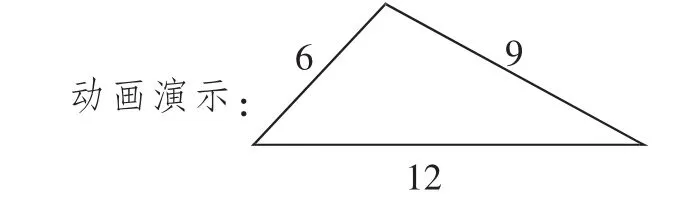
师:见证奇迹的时刻到了。(教师操作课件,拖动红色的线段)
师:长了吗?13厘米是可以的,继续拉长,这个三角形的样子好像在变哦。

师:14也是可以的,这个三角形变得越来越——
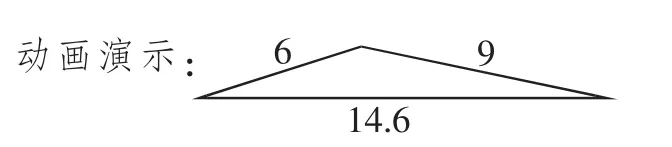
生:越来越扁了。
师:继续拉长到14.95cm、14.97cm、14.98cm、14.99cm呢?(学生想象、交流)
刚刚有人说15厘米可以,想象下,如果拉长到15厘米,会是什么样?(学生思考、交流)
动画演示验证:

生:平了(成一条线)。
师:15厘米可以围成三角形吗?
生:不可以。
师:果然跟你们想的一样,看来我们要把这个问号擦掉了,可以肯定15厘米是不行的。(教师更改板书)你们真厉害,如果再长一点点呢?会是什么样?
生1:会连不上。
生2:会回去。
师:是不是跟你们想的一样呢?
动画演示:

师:它怎么了?
生:断掉。
师:为什么会这样呢?
生:红色的太长了,那两条线段连不上了。
师:想要拉上怎么办?
生:往回拉。
师:好,那我们往回拉试试看(教师操作课件:开始回拉)什么时候又会出现三角形呢?
生1:14.9。
生2:14.99也行。
师:你们想得越来越精准了,也就是说——
生:只要比15小就行了。
师:概括得真好,掌声。
师:三角形又出现了,继续变短,11、10、9…都是可以的,再看看这个三角形,变得越来越——
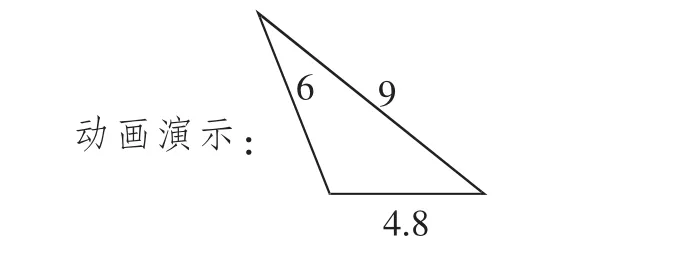
师:刚刚3厘米我们是存在争议的,认为3厘米不能围成的请坐好,认为3厘米能够围成的请起立。

师:我们继续看,三角形的样子又变了!它好像又要——
生:倒了。
师:3到底能不能围成?(学生思考、交流)
生1:我觉得到了3厘米就又成为一条线段,围不成了。
生2:我觉得到了3厘米就又平了。

师:能围成吗?
生:不能。
师:3厘米的时候啊,也是围不成三角形的。如果继续变短呢?
生:更不能围成。
(四)归纳推理,建立三角形三边关系模型
师:除了把红色的小棒适当延长能围成三角形,刚刚你们还想了什么办法?
生:换另一条边。
师:那就固定2厘米、6厘米两根小棒,那第三条边的范围是多少呢?

生:比4大,比8小(教师板书:4<□<8)。
师:为什么?
生:2加6等于8(教师板书:6+2)
师:8也就是这两条边的和。那4呢?
生:6-2。
师:其实也就是这两条边的差。(教师板书:6-2)
师:那我们就带着这种感觉继续来看,如果固定2厘米、9厘米这两根小棒,你能很快想出第三边的范围吗?

生:大于7,小于11。
师:7怎么来的,11呢?
生:9减2等于7,9加2等于11。
师:同学们,探究到这,能说说你有什么发现吗?
小结:看来啊,要围成三角形,第三条边最长要比另两边之和小,最短要比他俩的差要大。
二、思考与认识
1.改进学习材料,搭建思维阶梯,驱动学生思考
为什么我们选择操作实验的路径来教学“三角形三边关系”时,学生总是很难将思维聚焦于两边之和与第三边的关系上。难道真的是路径选择错误,只能用初中的线段公理教学吗?纵观以往的各种教学案例,我们就发现,大部分教师在课堂上都是提供几组任意长度的三条线段(或是用一根整厘米的线段来任剪三段)让学生操作探究,我想这才是导致学生学习难点产生的根本原因。因为从数学本质上分析,这里涉及一个三元函数的问题,当我们选取任意的三条线段的长度a、b、c时,就等同于函数的三个变量。找到问题的症结就好办了,只需顺应学生思维,改进学习材料即可。因此,将实验设计成固定长度为9cm和6cm的蓝、绿两根小棒,用直尺代替第三根(红色)小棒,只观察第三根小棒的长度范围。学生在操作、观察、验证的过程中,直观地发现第三条线段超过15厘米时,蓝、绿两根小棒就接不上,不能围成三角形,比3厘米短时,蓝、绿两根小棒就会有凸出来的部分,也围不成三角形。由此,就帮助学生在思维阻滞处搭建了一个脚手架,让其顺理成章地感知要围成一个三角形,就必须用“两边的和与第三边比较”。
“深度学习”的课堂倡导数学课要有浓浓的思考味,就须想得更清晰、更全面、更深刻,达到“理性地思维”。于是,在第一个操作实验后,教师在学生对三边关系有了初步感知的基础上,继续引发深度思考,接着追问:想想看,如果固定长度为2cm和6cm红、绿两根小棒,那么第三根小棒的长度范围是多少?学生原来觉得已经清晰的认知,再次遇到阻碍,又陷入沉思之中。经过独立思考、师生交流,再次建立认知平衡,蓝色小棒要在4cm和8cm范围内。到这个环节,应该说学生联系前面的经验,通过想象,再到动画的演示验证,已基本理解了第三条边的取值范围,但离深刻理解三角形三边关系性质还有距离。在此基础上,教师有了第三次追问:如果红、蓝两边不变,绿色边的长度又在什么范围?通过一而再地追问,给学生不断地搭建思维的新台阶,促使学生将新积累的经验积极地迁移到新的问题中,使学生的思考更全面、更理性,对知识的建构更深刻。
2.借助信息技术,聚焦学生思维,巧妙突破难点
采用数学实验操作探究三角形三边关系这一方法时,在教学中有一个难点:当两边之和等于第三边时,由于小棒不够细,学生经常误以为是能够围成的。而老师在此环节颇费心思:有的不断改进学具,从小棒到牙签,要多细有多细;有的则反其道而行,改用透明胶片或长方形纸条,同时辅助多媒体、放大镜试图减少误差,让学生观察到还有一点缝隙,此时是不能围成三角形的。老师煞费苦心,效果却差强人意。须知在数学学习过程中任何一个深刻的理解不可能是一蹴而就的,只有学生在学习活动过程中及时加以调整和修正,澄清关于这个知识的疑虑,才能形成正确的数学知识。“两边之和等于第三边是不能围成三角形的”这个难点的突破也经历这样一个过程。在操作探究后对于两边之和能不能围成三角形,学生思维是有疑虑的,大部分学生在操作、观察的基础上认为是能围成的。这个环节,教师不急于给出方向的引导,而是“慢”下来,让学生的思维在此处“飞”了一会儿。先用动画演示:当红色线段依次为12cm、13cm、14cm长度时,观察三角形有什么变化,并及时追问:想想继续拉长到14.5cm、14.9cm时,三角形又会怎么变?继续拉长到14.95cm、14.97cm、14.98cm、14.99cm呢?如果不拉你能想象到三角形的变化吗?等学生脑中逐步有了图像,再用动画演示验证。这样通过不断调整、修正,使得学生思维发展从混沌到清晰有了可能。在这个基础上接着追问:“如果拉长到15会怎么样?”通过一系列的问题引发学生的思考和想象,再用动画验证,层层递进,突破难点,把三角形三边知识一步步引向深入。在学生思维困顿之处,留时间,给空间,搭支架,让学生自己去发现规律、纠正和补充错误或片面的认识,加深对所学内容的理解。
总之,小学数学教学应围绕“让学习真正发生”来充分展开,深度关注新知识本身蕴含的潜在意义、学生的背景知识和情感体验、学生学习的认知策略,让新知识的组织与呈现方式交融在一起,学生的学习才会显得更具生命力。♪

