Hydro-mechanical behavior of an argillaceous limestone considered as a potential host formation for radioactive waste disposal

T.S.Nguyen,Zhenze Li,Grnt Su,M.H.B.Nsseri,R.P.Young

aCanadian Nuclear Safety Commission,Ottawa,Canada

bDepartment of Civil Engineering,University of Toronto,Toronto,Canada

Keywords:Hydro-mechanical behavior Excavation damage Deep geological repository(DGR)Limestone Poro-elasto-plasticity

A B S T R A C T The Canadian Nuclear Safety Commission(CNSC),Canada’s nuclear regulator,conducts regulatory research in order to develop independent knowledge on safety aspects related to the deep geological disposal of radioactive wastes.In Canada,the Cobourg limestone of the Michigan Basin is currently considered as a potential host formation for geological disposal.The understanding of the hydromechanical behavior of such a host rock is one of the essential requirements for the assessment of its performance as a barrier against radionuclide migration.The excavation of galleries and shafts of a deep geological repository(DGR)can induce damage to the surrounding rock.The excavation damaged zone(EDZ)has higher permeability and reduced strength compared to the undisturbed rock and those factors must be considered in the design and safety assessment of the DGR.The extent and characteristics of the EDZ depend on the size of the opening,the rock type and its properties,and the in situ stresses,among other factors.In addition,the extent and characteristics of the EDZ can change with time due to rock strength degradation,evolution of fractures within the EDZ,and the redistribution of pore pressure around the excavation.In this research project initiated by the CNSC,the authors conducted experimental and theoretical research in order to assess the hydro-mechanical behavior of the Cobourg limestone under undamaged and damaged conditions,both in the short and long terms.The short-term behavior was investigated by a program of triaxial tests with the measurement of permeability evolution on specimens of Cobourg limestone.The authors formulate a coupled hydro-mechanical model to simulate the stress-strain response and evolution of the permeability during those triaxial tests.Using creep and relaxation data from a similar limestone,the model was extended to include its long-term strength degradation.The model successfully simulated both the short-and long-term hydro-mechanical behavior of the limestone during those tests.This provides confidence that the main physical processes have been adequately understood and formulated.

1.Introduction

In many countries,deep geological disposal is the preferred option for the long-term management of radioactive waste resulting from the operation of nuclear power plants.A deep geological repository(DGR)relies on a multi-barrier system in order to contain and isolate the waste from the surface environment for very long periods of time.The host rock formation is an important component of this multi-barrier system.The excavation of galleries and shafts of a DGR can induce damage to the surrounding rock.The excavation damaged zone(EDZ)has higher permeability and reduced strength compared to the undisturbed rock and those factors must be considered in the design and safety assessment of the DGR.During the operational period of the DGR,theEDZ must be taken into account in the design of ground control measures in order to protect the workers.In the post-closure period,the EDZ with its enhanced permeability potentially constitutes preferential pathways for radionuclide migration.Due to the above safety considerations,the EDZ has been the subject of many research activities covering both experimental and theoretical aspects(Soennke et al.,1998;Bossart et al.,2002,2004;Shao et al.,2008).A comprehensive review can be found in Tsang et al.(2005)with respect to relevant processes,associated factors,and modeling and testing techniques on permeability of EDZs in various rock types.The main conclusions commonly drawn from the past studies on EDZ are that:(1)The shape and extent of an EDZ are site-specific and can be correlated with the size of the opening,rock type and its mechanical property and anisotropy,and in situ stresses,among others;(2)Strong local heterogeneity in the EDZ has been observed by several studies(Soennke et al.,1998;Bossart et al.,2002);and(3)Permeability increase in an EDZ is caused by damage to the rock in the EDZ,and the permeability of an EDZ will increase significantly near the excavation surface and decrease to the level of intact rock with distance away from the excavation surface(e.g.Autio et al.,2006;Van Geet et al.,2008;Cho et al.,2013).The largest increase in permeability of an EDZ in indurated clay rock has been reported to be six orders of magnitude higher than that of intact rock(Tsang et al.,2005),while an increase in permeability of an EDZ between 2 and 4 orders of magnitude higher than that of intact rocks has also been reported for various rocks measured either from site investigations or laboratory experiments(Shao et al.,2008;Van Geet et al.,2008;Zhang,2015).

Studies on the EDZ as reported in the above references are concerned with crystalline rocks,or claystones which are being considered in Europe as host rock formations.In Canada,in addition to crystalline rocks of the Canadian Shield,the Cobourg limestone of the Michigan Basin in Southern Ontario(Fig.1)is also a candidate host formation for the geological disposal of radioactive wastes(NWMO,2011).The Cobourg limestone is a mottled light to dark grey,very fine-to coarse-grained,very hard,fossiliferous argillaceous limestone and is characterized by a nodular fabric and bioturbated bedding surfaces with minor intraformational variation(NWMO,2011).It has high uniaxial compressive strength(UCS),very low permeability,and high chemical sorption potential.It is also overlain by multiple layers of low-permeability and highlysorptive shales.The host rock and the overlying shale cap rocks,in their undisturbed state,together would provide an important barrier for radionuclide migration.

As compared to claystones and crystalline rocks,there are relatively fewer systematic studies on the hydro-mechanical behavior of the Cobourg limestone in support of the assessment of the EDZ around repositories in such formations.Damjanac et al.(2012)used the results of UCS tests in order to simulate the extent of the EDZ around a proposed DGR for low and intermediate level waste(LILW),assuming that the long-term strength of the rock is determined by the crack initiation(CI)threshold,which is on average equal to 45%of the UCS.Damjanac et al.(2012)found that from the combined effects of excavation,seismic activity and future glaciation,the EDZ would be contained in the Cobourg limestone and not extend to the overlying cap rock shale.Perras and Diederichs(2016)used the damage initiation and spalling limit(DISL)approach to predict the EDZ around circular openings in the Cobourg limestone.These authors differentiated between a highly damaged zone(HDZ)with interconnected macrostructures,an inner EDZ(EDZi)with connected damage,and the outer EDZ(EDZo)with isolated damage.Estimates of the radial extent of each zone as a function of the ratio of the maximum tangential stress to CI were provided.

Fig.1.Cross-section of the Michigan Basin showing the location of a proposed deep geological repository for low and intermediate level waste.Approximate 50×vertical exaggeration(NWMO,2011).

Mathematical models such as in Damjanac et al.(2012)and Perras and Diederichs(2016)need constant improvement when more experimental data from laboratory or field tests are available.In particular,constitutive relationships for the stress-strain strength behavior of the Cobourg limestone need to be improved with updated experimental information for calibration,verification and parameter derivation.Recent laboratory experiments to provide such data consist of laboratory uniaxial and triaxial tests,some with measurements of permeability,uniaxial creep tests and longterm strength tests.The results of these experiments show that:

(1)The Cobourg limestone is inherently anisotropic and heterogeneous(Nasseri et al.,2013;NWMO,2014;Ghazvinian et al.,2015).Anisotropy is due to stratification resulting from the sedimentation process.Heterogeneity originates from the interspersed fabric of a calcite,dolomite-rich light gray limestone nodules separated by dark gray argillaceous wisps and inclusions that approximately mark the bedding.In uniaxial and triaxial loadings,macrocracks formed at failure and are preferentially distributed in the dark argillaceous inclusions(Selvadurai and Giowacki,2017).

(2)The changes in permeability of the Cobourg limestone with the stress state and temperature were determined by the pulse pressure methods by Nasseri et al.(2013)and Selvadurai and Giowacki(2017).With increasing hydrostatic stress,or increasing temperature under confined conditions,the permeability decreases due to pore space reduction and microcracks closing.With increasing deviatoric stress,following an initial decrease of permeability due to volume compression,there is an increase in permeability due to damage by up to four orders of magnitude at the residual stress level,after failure.The high post-peak permeability is due to the presence of cracks that form preferentially in the weaker dark gray argillaceous band(Selvadurai and Jenner,2013;Selvadurai and Giowacki,2017).

(3)The stress-strain-strength behavior of the Cobourg limestone is time-dependent(Paraskevopoulou et al.,2017).Creep tests under constant uniaxial loads show the increases of both the axial and radial strains,following in general the three classical stages of primary,secondary and tertiary creep(at high stress levels),with sometimes the absence of the secondary phase.The time to failure of different samples was recorded.When the load is equal to the UCS,the sample fails instantly.At load levels below the CI(estimated at 40%of UCS),no failure is observed for up to 100 d.At load levels above the crack damage(CD)threshold,which was estimated at 80%of the UCS,the samples fail within minutes to an hour.Stress levels between the CI and CD present an uncertain situation with respect to failure,with samples loaded under 70%UCS not failing within 100 d.Long-term strength data for the Cobourg limestone were complemented with data from a similar rock,i.e.the Jura limestone.The time of failure versus the ratio of stress to UCS shows aunique relationship for both types of limestone.

In this research project initiated by the CNSC,the authors conducted experimental and theoretical research in order to gain further insights into the hydro-mechanical behavior of the Cobourg limestone under undamaged and damaged conditions,both in the short and long terms.In order to confirm the results from Nasseri et al.(2013)and Selvadurai and Giowacki(2017),the short-term behavior was investigated by a program of triaxial tests with the measurement of permeability evolution on specimens of Cobourg limestone.The authors formulate a coupled hydro-mechanical model in order to perform interpretative simulation of the stressstrain response and evolution of the permeability during those triaxial tests.For the long-term behavior,the authors used test data from Paraskevopoulou et al.(2017)in order to take into account viscosity and long-term strength degradation.This paper will present the authors’experimental program of triaxial tests with permeability measurement,the development of a mathematical model to interpret the above tests,and the extension of the model to take into account time-dependent behavior.Through the above activities,the authors aimed to verify conclusions reached by others,further the understanding of key processes influencing the hydro-mechanical behavior of the Cobourg limestone,and identify the areas that need further investigation.Some of the authors(Le and Nguyen,2015;Nguyen and Le,2015a;b;Li et al.,2017)have previously investigated the hydro-mechanical behavior of different types of sedimentary argillaceous rocks,i.e.the Opalinus Clay and the Tournemire shale.The Cobourg limestone possesses important clay content;however,it is more brittle and stronger than the above-mentioned rock types.A similar methodology to the one previously adopted to Opalinus Clay and Tournemire shale is utilized and adapted here in order to verify its limitations and identify areas of extension to the previously proposed framework.

2.Triaxial tests with permeability measurements

2.1.Experimental setup and procedure

An experimental program was developed in order to complement the available data on the hydro-mechanical behavior.The program was designed to explore the evolution of the permeability with progressive damage.The block samples for the experiment were collected at St.Mary’s Quarry,around 55 km northeast of Toronto,Ontario,Canada.The cylindrical testing specimens were cored parallel and perpendicular to the bedding plane.Porosity and density of the limestone were measured according to the ISRM standard procedure(Brown,1981).The specimens have a nominal diameter of 50.5 mm and length of 125 mm.

Triaxial tests were performed in the geophysical imaging cell(GIC),as shown in Fig.2,at the Rock Fracture Dynamics Facility(RFDF)of the University of Toronto at a room temperature of about 25°C.The axial loading rate was controlled at a strain rate of 1.6×10-6s-1both before and after the peak stress.The permeability of the specimens was measured with the pulse decay method(Brace et al.,1968)at different levels of applied axial stress.The servo-controlled load was kepton hold during the permeability measurement.A servo-controlled Quizix pump system(two pumps under independent constant control mode)was used to regulate the top and bottom pore pressures and to generate hydraulic pulses for permeability measurements.During the experiment,a 5 MPa confining pressure was applied and maintained,and a 3 MPa pore pressure(back pressure)was then applied to eliminating possible air in the system.The pore pressure decay at one end of the sample was then measured by introducing an additional 1 MPa hydraulic pulse.The pressure gradient decays exponentially to zero,and the permeability of the rock sample was estimated from the decay curve using the methodology in Brace et al.(1968).

2.2.Experimental results

The experimental results for the three Cobourg limestone specimens with axial loading parallel to the bedding planes show failure stresses of 90 MPa,99 MPa and 77 MPa,respectively(Fig.3a),while the three specimens with axial loading perpendicular to the bedding planes show failure stresses of 56 MPa,46 MPa and 46 MPa,respectively(Fig.3b),at the 5 MPa confining pressure.The former three specimens show smaller axial deformations at peak than that of the latter three specimens.Our results are in the range of UCS between 40 MPa and 120 MPa tested by others(NWMO,2014;Ghazvinian et al.,2015)and also confirm that the direction of loading with respect to the bedding orientation influences the mechanical response.The effect of heterogeneity is however out of the scope of this study and will be examined in future research.

Fig.2.Internal view of the geophysical imaging cell with rock specimen as well as the confining rubber and the X-,Y-and Z-direction velocity stacks.LVDT is the linear variable differential transformer.All dimensions are in inch.

Fig.4 shows the variation of the permeability as a function of axial stress for all six Cobourg limestone specimens.The variation trend of the permeability is characterized bysimilar features at prefailure.The initial section of the curves is characterized by a higher value of permeability(measured with very small differential stresses or under a hydrostatic stress).The second section of the curves is characterized by a decreasing trend of permeability when the specimens are at a compressive regime.The third section of the curves shows an increase in permeability value at a much higher compressive stress prior to the peak strength,which is associated with the initiation and coalescence of microcracks.The permeability values at post-failure show either an increase or decrease depending on how and where the induced hydraulic pulses detect the newly formed network of fractures or where the failure surfaces become more impervious due to creation of gouge materials.Distinguishing the two situations from each other requires more detailed investigation.However,the measured permeability of the intact Cobourg limestone does not show significant difference for the six specimens.The permeability measured at post-failure is 2-3 orders of magnitude higher than that of the intact rock.This means that the permeability of the highly damaged limestone due to excavation could be at least 3 orders of magnitude higher than that of the undamaged rock.The variation of permeabilitykas a function of rock damage is confirmed by the evolution of wave velocity measurements and supported by the thin-section image of microcracks and macrocracks observed at post-failure.The general trend and magnitude of permeability evolution found in this study are consistent with findings from others(Nasseri et al.,2013;Selvadurai and Jenner,2013;Selvadurai and Giowacki,2017).

3.Modeling the short-term hydro-mechanical behavior

A mathematical model was developed to interpret the results of the above triaxial tests with permeability measurements.The main assumptions used in developing the model are described as follows:

(1)The universal laws of mass and momentum conservation are invoked.

(2)The rock mass is conceptualized as a transversely isotropic porous medium.The Cobourg limestone is a sedimentary rock for which bedding and the presence of randomly distributed clay inclusions can induce inherent anisotropy in both its hydraulic and mechanical behavior.The effect of bedding in sedimentary rocks has been studied and modeled elsewhere (Nguyen and Le,2015a;Pietruszczak and Haghighat,2015)and we adopted the same approach to these authors,where the principal directions of the microstructure of the rock,one perpendicular and two parallel to the bedding orientation,are defined.The anisotropy induced by the clay inclusions are not considered in the present paper and will be the subject of future studies.

Fig.3.Stress-strain relationships of limestone specimens with loading(a)parallel and(b)perpendicular to bedding planes.

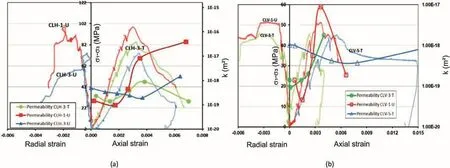
Fig.4.Evolution of permeability with axial strain for loaded(a)parallel and(b)perpendicular to the bedding planes(note the stress-strain curves for the same three specimens are shown in the background with faded similar colour).

(3)The fluid flow in porous media is assumed to be saturated and is governed by Darcy’s law:

where u is the liquid water velocity vector;κis the permeability tensor written in matrix form;μand ρfare the water viscosity and density,respectively;and g is the acceleration of gravity.Furthermore,the permeability is assumed to vary with volumetric deformation and damage as discussed later in the paper.

(4)A nonlinear stress-strain relationship based on the classical theory of plasticity is adopted and will be described in more detail in this paper.The onset of irrecoverable deformation is determined by the Drucker-Prager yield criterion,with strain hardening up to the peak stress.Strain softening with a nonlocal plastic deformation(Baˇzant and Pijaudier-Cabot,1989;Jirásek,2002;Aifantis,2011;Antolovich and Armstrong,2014;Pijaudier-Cabot and Grégoire,2014)is assumed for the post-peak behavior in order to simulate strain localization.

(5)Biot’s effective stress principle is used to account for the effect of pore pressure.Within the framework of poroelasticity,the total stress(σij)in a porous medium saturated with pore fluid is decomposed into effective stressand pore pressure(p):

where δijis the Kronecker delta,and α is the Biot’s effective stress coefficient given by

whereKDis the drained bulk modulus of the porous media andKsis the bulk modulus of the solid material.

Based on the above assumptions,and following the methodology used by Nguyen and Selvadurai(1995),the governing equations of the model are developed as follows:

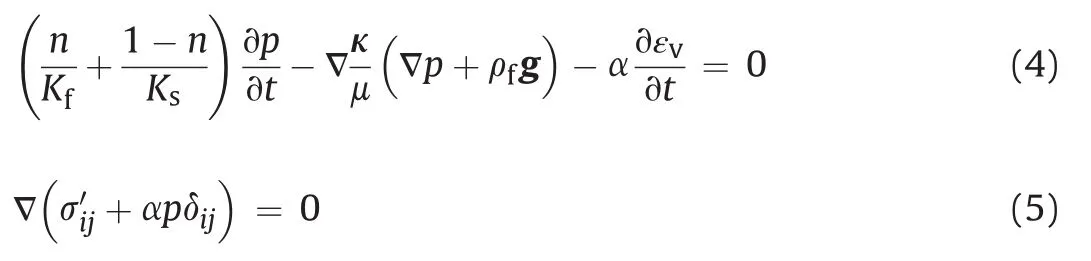
wherenis the porosity,Kfis the bulk modulus of the fluid,tis the time,and εvis the volumetric strain.Eqs.(4)and(5)respectively express the mass conservation of the pore fluid,and the conservation of momentum of the porous skeleton,in which inertial effects are neglected.

3.1.Constitutive relationship for the porous skeleton

The governing equations must be complemented by the adoption of a constitutive relationship that relates the stress tensor to the strain tensor.Similarly to other authors(Haghighat and Pietruszczak,2015;Nguyen and Le,2015a;Li et al.,2017),the model is developed within the framework of elasto-plasticity theory,using the Drucker-Prager yield criterion that is formulated to include strain-hardening of the yield parameters.Before yielding starts,the material is assumed to be elastic.This results in an equation that relates the effective stress increment to the strain increment:

where dσ′is the increment of the effective stress tensor(written as a vector),dε is the increment of total strain tensor(written as a vector),and dεpis the increment of the plastic strain tensor(written as a vector).

For a transversely isotropic material,the elastic stiffness tensor is defined by five independent parameters,for example,two Young’s moduliE//andETand three Poisson’s ratios ν.In addition,damage is considered by assuming that the Young’s moduli decrease exponentially with the effective plastic strain,as discussed next.

The plastic strain component is determined as follows.

3.1.1.Determination of the plastic strain

The Drucker-Prager yield criterion matching the Mohr-Coulomb criterion at the compressive meridians can be written using the following form:

whereI1is the first invariant of the stress tensor,J2is the second invariant of the deviatoric stress tensor,cis the cohesion,andφis the friction angle.

When the yield criterion is reached,plastic strain occurs.The plastic strain is derived from the plastic potential equation.Here,a nonassociative flow rule is used,with the plastic potential taking the same form as the yield criterion where the friction angle is replaced by the dilation angleψ:

In this regard,the plastic strain rate is given by

whereλis the consistency parameter.

The effective plastic strain can be defined as(Simo and Hughes,1998):

It is assumed that damage is induced by a combination of plastic strain and tensile stress,resulting in a degradation of the Young’s modulus.A dilatational volumetric strain,εvol,is defined so that when tensile mean effective stress occurs,εvolcan be determined(εvolis equal to the total volumetric strain when the latter is positive indicating tension;it is equal to zero otherwise).

Using the effective plastic strain and dilatational volumetric strain as a measure of damage,the Young’s moduli are assumed to degrade as follows:

whereEiis the initial tangent modulus.The two parameters are best fit from analysis of the experimental results.It is assumed that geomaterials have negligible tensile strength,therefore,damage is induced when the effective mean stress becomes tensile,resulting in an increase in permeability. The Young’s moduli in different directions can vary differently. However, for simplicity, it was assumed that their evolution follows the same functional form and that assumption seems to fit the purpose of the proposed interpretative model.

3.1.2.Yield function parameters

Martin and Chandler(1994)and Nguyen and Le(2015a)stipulated that the cohesion,c,degrades with accumulated irrecoverable

Following Nguyen and Le(2015a),the model selects the effective plastic strain as an internal variable;therefore,the cohesion and friction angle can be produced as a function of plastic strain:(plastic)strain while the mobilized friction angle,φ,increases to a maximum value that accounts for interlocking effects before decreasing to a residual value(see Fig.5).Based on this observation,the fitting ofcand φ）will be determined based on the initial yield,interlocking and residual points(Martin and Chandler,1994;Nguyen and Le,2015a).

For all specimens used in the triaxial compression test,the change ofcis assumed to follow an exponential law:

where subscript r denotes the residual state,0 denotes the initial state,and i denotes the interlocking;εiis the strain at which the maximum friction occurs;andAcandAφare the decay factors calibrated from the experimental stress-strain curves.This calibration was performed by iteratively running the numerical simulation of triaxial tests using different values of the above decay factors,until a good match was obtained with the experimental stress-strain curves.The best- fit values for bothAcandAφthus obtained were 30.

3.1.3.Microstructure tensor approach for yield parameters

The existence of bedding in Cobourg limestone results in inherent anisotropy of its yield parameters.When the bedding exists in only one direction,the anisotropy reduces to a case of transverse isotropy,with two principal directions parallel to bedding,and the third being perpendicular to it.As in Nguyen and Le(2015a),we used the microstructure tensor approach of Pietruszczak and Mroz(2001)in order to take into account the transverse isotropy of the yield parameters.In that approach,a generalized loading vector is first defined from the stress tensor as

where(α=1,2,3)is the base vector in the principal direction of the transverse isotropy.The unit vector alongLiis given by

Fig.5.Evolution of cohesion and friction angle in conventional triaxial tests.φris the residual friction angle,andφiis the increment of friction due to interlocking.

The loading unit vectorliis an indicator of the relative orientation between the stress tensor and the principal directions of the transverse isotropy.In order to take into account the transverse isotropy in plastic yield,the yield parameterscandφare expressed as a function ofli:

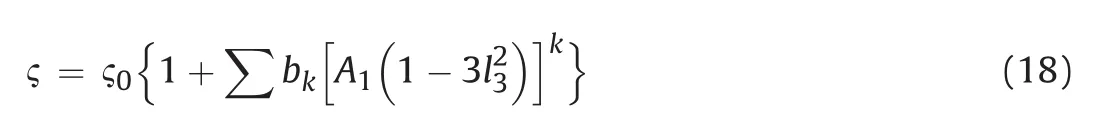
where ςstands for eithercorφ;A1,bnand ς0are the model parameters;kis a summation index;andl3is the component of the loading unit vector in the direction perpendicular to bedding.A detailed methodology to derive the model parameters is given by Nguyen and Le(2015a).A complete set of experimental data from triaxial tests performed at no less than three loading directions would be needed.In this experimental program,there were only two loading directions,perpendicular and parallel to bedding.Although bothcandφshould be directionally dependent,in this paper,due to a lack of data in a third loading direction,we only consider parameterφ.By analogy to Eq.(18),that parameter is expressed as a function of the loading unit vector as follows,providing the best fit to the stress-strain behavior as discussed later:

This treatment proves sufficient to reflect the peak strength and stress-strain behavior of the Cobourg limestone under the two tested loading orientations of the current set of experimental data.

3.1.4.Post-peak behavior using a nonlocal continuum approach

Various plasticity phenomena,strength properties,shear band,and crack tip propagation have been found to display size effect(Baˇzant and Pijaudier-Cabot,1989;Fleck et al.,1994;Jirásek,2002).Smaller samples have higher strength than similar larger samples.The mechanical properties of crystalline materials are found to be related to grain sizes,including the constitutive behavior and physical mechanism of strength,plasticity,shear localization,fatigue and creep(Meyers et al.,2006).It is generally believed that microscale crystallization contributes to the overall strengthening of materials,which can be interpreted with theories involving a characteristic length.

Local continuum model with strain-softening constitutive law would cause loss of ellipticity of the governing differential equations,ill-posedness and localization of damage into a zero volume zone,and the mesh-dependence for finite element simulations(Jirásek,2002).The fracture may appear to be localized in a narrow crack,however,the determining factors underlying the initiation,coalescence and interconnection of fracturing involve nonlocal homogenization and energy release from a finite volume surrounding the microcrack.Some causes of nonlocality have been illustrated by Baˇzant and Jirásek(2002)as a result of heterogeneity of microstructure,interaction between microcracks,and the intrinsic statistical distribution of microcracks.

We apply a well-known regularized procedure to accommodate the singularity problem for localization(Baˇzant and Jirásek,2002;Jirásek,2002;Forest,2008).The basic idea is to let the sharp contrast of deformation across shear bands diffuse into the surrounding domain,with the consideration of a certain influence range that has sound physical meaning.This allows the singularity problem to be circumvented in numerical simulations.

Similar to other authors(Baˇzant and Jirásek,2002;Jirásek,2002;Pijaudier-Cabot and Grégoire,2014),a nonlocal plastic strain is defined,and is determined from the solution to the Helmholtz equation:

wherelcis the characteristic length indicating the influence zone,andis the nonlocal equivalent plastic strain.

The boundary condition of the above differential equation is taken as a homogeneous Neumann boundary:

where n is the vector normal to the boundary.

A linear weighting function is used to harmonize the integrated effect of both plastic strain and its gradient,which is given as(Jirásek,2002):

whereγis the plastic strain measure,andm′is a weighting factor.This form is proposed in this study to consist of two components,i.e.the effective plastic strain,,and the regularized plastic strain measure,,to evaluate the combined influence of effective plastic strain and the effective elastic strain gradient.The plastic strain measureγis then used in lieu of the effective plastic strain in the strain-hardening equations(Eqs.(14)and(15)).

3.2.Transient pressure pulse decay test for permeability estimation

The transient pressure pulse method(Brace et al.,1968),as illustrated in Fig.6,has been used to test the permeability of tight rock and concrete with extremely low permeability.In this technique,the rock sample is placed in a confined chamber and is connected to two fluid reservoirs on the upstream and downstream sides.At timet=0,a small pressure pulse is introduced to the upstream reservoir and the decay of pressure with time is monitored.The permeability of the test sample,as shown in Fig.7,is estimated with an exponential decay function based on the analytical solution provided in Brace et al.(1968).This analytical solution is however based on the simplified assumption that the initial pore pressure in the sample is uniform and is equal to the pressure in the reservoirs,before the introduction of the pulse.The analytical solution also assumes that the sample is homogeneous,with a uniform permeability.As will be discussed later,this assumption is not representative of the actual conditions since triaxial loading produces heterogeneous damage in the sample,inducing a non-uniform distribution of permeability.Due to the above factors,in this paper,we also solved the governing equations with the finite element method in order to simulate the pulse tests together with the triaxial tests.The pore pressure distribution in the sample before the start of each pulse test is dependent on the poroelastic parameters which will be discussed later.One important parameter in the proposed model is the Biot’s coefficient α.Whenαis close to 1,the pore pressure induced by loading is higher;when it is close to zero,the pore pressure generated by loading is negligible.

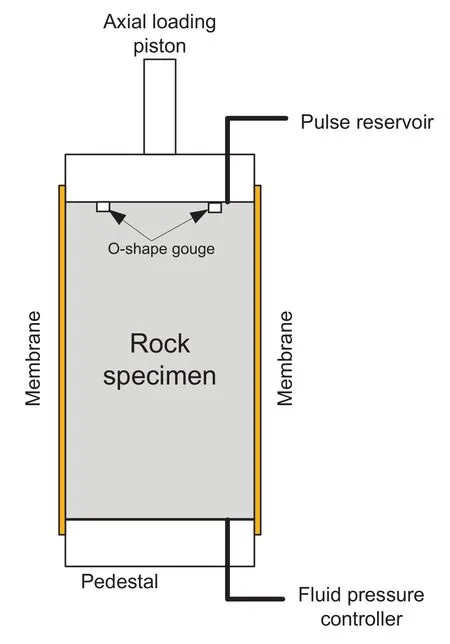
Fig.6.The confined sample arrangement used in transient pulse test.

Fig.7.Biot’s coefficient as a function of porosity for various rock types and comparison with HS bounds.Calculation involves Kf=2.4 GPa,Ks=75 GPa,P-wave velocity VP=5.5 km/s,density of solids ρs=2700 kg/m3and Poisson’s ratio ν=0.45.Data are cited from Cosenza et al.(2002),Alam et al.(2012),and Hasanov et al.(2015).

Biot’s coefficient is an important parameter that governs the pore pressure generation in a saturated sample during triaxial loading.During both isotropic and deviatoric loadings,the pore pressure would increase in the sample and would not fully dissipate if drainage is impeded.At the start of the pulse tests performed in the experimental program reported in this paper,there might be residual pore pressure from the previous loading level.The magnitude of that residual pore pressure largely depends on the Biot’s coefficient.To the authors’knowledge,no direct measurements of the Biot’s coefficient have been conducted for the Cobourg limestone at this time.The classical expression for the Biot’s coefficient is given in Eq.(3).However,in that equation,Ks,the bulk modulus of the minerals,is very difficult to estimate since the mineral composition of the Cobourg limestone is very heterogeneous.On the other hand,it is well recognized that porosity has a large influence on the Biot’s coefficient.Hashin and Shtrikman(1963)and Zimmerman et al.(1986)estimated upper and lower bounds of Biot’s coefficient as a function of porosity using the Skempton’s coefficientBas an additional dependent variable.

Fig.7 shows the reported Biot’s coefficients for various rocks and the comparison with the Hashin and Shtrikman(HS)bounds.It is clearly demonstrated that the Biot’s coefficients of rock depend strongly on its porosity especially when the porosity becomes very small.Biot’s coefficient around 0.7-0.95 is only found for highly porous rocks with porosity ranging from 0.1 to 0.4.For the Cobourg limestone,the porosity is less than 0.01 which implies a much lower value in Biot’s coefficient in the range of 0.06-0.2.There is evidence from the current set of tests that Biot’s coefficient should indeed be low.At the start of each pulse test,it was found that there is negligible residual pressure from the axial loading.With a Biot’s coefficient of around 0.7,that residual pressure should be important,even if the compressibility of the pore fluid has been increased by the authors by a factor larger than 10.In addition,one can also use the basic definition of Biot’s coefficient(Eq.(3))in order to obtain a complementary estimate of Biot’s coefficient.The drained bulk modulusKDcan be estimated from the stress-strain curves provided by the triaxial tests at an average value of 20 GPa.There is an important amount of argillaceous content in the mineralogy of the Cobourg samples,in a range of 20%-50%by volume(Ghazvinian et al.,2015).Assuming the calcite content to be 70%,and the argillaceous content to be 30%,Kscould be estimated from the volume average between the bulk modulus of calcite(of the order of 77 GPa)and the one of the clay minerals(of the order of 8 GPa)resulting inKs=23.6 GPa.Using Eq.(3),one obtains a Biot’s coefficient equal to 0.07,which is close to the previous estimate from porosity.Reported values of Biot’s coefficient for the Cobourg limestone were much higher(Selvadurai and Najari,2016)than the values suggested in this work.Furthermore,Biot’s coefficient could also be damagesusceptible.The above aspects need further experimental and theoretical investigations.

3.3.Permeability of damage zone

The permeability of damaged rock is found to depend on various factors,including the resultant porosity,the size of the crack openings,the confining pressure,the volumetric change in postpeak stage,and the moisture content.In the current elasto-plastic framework as developed in this study,the adopted plastic flow function contributes to the dilatancy in volumetric strain.The confining pressure was maintained constant during the triaxial test,and samples weresaturated with water.Therefore,the damage factor becomes the most obvious factor pertinent to the permeability evolution of a damaged sample.An exponential relationship(Maleki and Pouya,2010)is applicable to this study and is given as

wherek0is the intrinsic permeability of the rock at the initial state;Ap,AvandAtare the model constants;andΘis an indicator of tensile failure and is given as

whereftis the tensile strength withft=1 MPa and 8 MPa for β =90°and 0°,respectively.

It is clear that the permeability is a function of the mechanical damage that depends on the effective plastic strain,volumetric variation,and extent of tensile cracking.Permeability can also be empirically correlated to stress level to reflect the initial crack closure stage(Tang et al.,2002).

The above relationship has been calibrated by numerical simulation against triaxial test data on Cobourg limestone,resulting in a set of parameters given asAt=4.34,Av=200,and a power-type step function for parameterApgiven as

where threshold value for permeability evolution is determined from backward analysis by best- fitting the pulse decay test data,ε0= εi/2,with εithe plastic strain corresponding to the crack damage threshold value.

3.4.Modeling results for the short-term hydro-mechanical response of Cobourg limestone in laboratory triaxial tests

The mathematical model previously described was implemented in a commercial finite element code,COMSOL Multiphysics(COMSOL,2017),in order to simulate the triaxial tests and the point wise pressure tests as previously described.COMSOL Multiphysics is a high-level programming language that numerically solves the governing equations(Eqs.(4)and(5)),along with all auxiliary equations that come from the assumed constitutive relationships,and the appropriate boundary conditions.The COMSOL finite element model with the mechanical and hydraulic boundary conditions is shown in Fig.8.The boundary conditions include a confining pressurePcapplied on the sidewall, fixed constraint for the bottom boundary,and a prescribed displacement on the top end.The sample was originally saturated with fluid before axial loading was applied.Other loading conditions include the vertical loading strain rate at 1.6×10-6s-1,with the target stress achieved within 2 s.The mobilized hardening/softening elasto-plastic model was integratedin the simulation.Table 1 lists the model parameters that have been obtained from either experiments or calibration with numerical modeling.For instance,the elasticity parameters were calculated by analysis of triaxial test data,and were found to be comparable with the reported data.All parameters in general would be orientation-dependent.To determine all parameters of the model,one would need a comprehensive and elaborate experimental program,consisting of at least three sets of triaxial tests in three different loading directions with respect to the bedding orientation.Each set should also include tests at different confining stresses and with permeability measurements as well.Examples of such parameter determination through a comprehensive laboratory testing program were given by Nguyen and Le(2015a)and Li et al.(2017).The present set of experimental data is not as comprehensive;therefore,the authors made simplified assumptions that only the Young’s moduli,the friction angle and the tensile strengthftare orientation-dependent.The Young’s moduli and the friction angle could be readily determined from the authors’experimental data.The tensile strength that is also orientation-dependent was inferred from Brazilian tests reported by Ghazvinian et al.(2015).

Fig.8.Boundary conditions for the triaxial test along with pulse decay permeability measurement.p1and p2are the upper and lower boundary pressures for the rock specimen,respectively;pbis the controlled boundary pressure;and Piis the initial pore pressure.

The confining pressurePcwas maintained at 5 MPa,and initial pore pressurePiat 3 MPa throughout the experiment,which resulted in an effective initial stress ofσi=2 MPa.Both ends of the test sample were applied with controlled fluid pressure atpb=3 MPa during the triaxial test,except when the pulse pressure decay test was conducted as the upper boundary was then supplied with a pulse of elevated fluid pressure to 4 MPa and then allowed to decrease with time(p1=f(t)).Hydromechanical coupling was considered in order to reflect the experimental conditions.The permeability of the damaged zone was updated on the basis of the stepwise function relating permeability with damage indicator of plastic strain as shown in Eqs.(23)and(24).

Table 1 Model constants for coupled hydro-mechanical modeling of permeation and triaxial test on Cobourg limestone.

3.4.1.Stress-strain response from triaxial loading

Fig.9 shows the modeling results for the stress-strain response to triaxial loading.The modeling results are found to reproduce the stress-strain behavior prior to the peak with very good agreement.The decrease in shear strength at post-failure stage compares well with the experimental results.Fig.10 shows the nonlocal deformation formed in post-failure stage as well as the distribution of tensile failure zones.Sharp contrast in compressive shear band can be clearly observed,demonstrating the ability of the proposed model in reflecting the nonlocal deformation.By comparison with the experimental observation of failure modes shown in Nasseri and Young(2016),the model consistently shows that:

(1)For β =0°,failure is a combination of sub-horizontal and low-angled fractures with respect to the horizontal;and

(2)For β =90°,failure appears to be a combination of subvertical and angled fractures.The fractures along the bedding plane,which is in the axial loading direction,are due to tensile failure.The tensile failure zone penetrates deep inside the rock specimen,and contributes to the permeability change significantly as it shortcuts the permeation pathway between the two fluid reservoirs during the pulse decay test.

The plastic yield function of Drucker-Prager criterion,with nonlocal plasticity,can only reproduce the compressive and shear failures.This needs to be complemented by a criterion for tensile failures.As shown in Fig.10b,the tensile damage zone is very limited for sample loading atβ =0°,but appears to be significant in volume and even extends to the top end boundary for sample loading atβ=90°.Therefore,the damaged permeability has to take both types of failure mechanisms into account,as shown in Eqs.(23)and(24).

3.4.2.Pulse decay test

As for the modeling of pulse decay tests that were performed at different stress levels,the boundary condition at the reservoir-rock interface differs from the classical Dirichlet or Neumann type.Therefore,an ordinary differential equation boundary was assigned to the upper boundary to accommodate the time and spatial derivatives of the fluid pressure.It is given as follows(Brace et al.,1968;Selvadurai and Carnaffan,1997;Liang et al.,2001):

Fig.9.Variation of deviatoric stress of Cobourg limestone with axial(ε1)and radial(εr)strains(confining pressure Pc=5 MPa,and initial pore pressure Pi=3 MPa).Solid lines are modeling results.Foliation of the specimen is oriented at angleβwith respect to the horizontal direction.Star-shaped points are where pulse tests were performed.

whereAis the cross-sectional area;V1is the upstream reservoir volume;andD=k/（μnχf）,in which χfis the compressibility of pore fluid.The initial condition of pore pressure takes the form ofPi=pb=3 MPa.

Fig.11a shows the comparison between the test data and the simulated pulse decay curves at different points during the triaxial test on Cobourg limestone.The simulation gives good agreement with the experimental observation,suggesting the validity of the proposed permeability function.Fig.11b and c shows the variation of the effective permeability estimated from the analytical solution from Brace et al.(1968)with increasing axial strain.The figures also show the arithmetic,geometric and harmonic means of the permeability derived from the finite element model.The initial decrease in permeability is attributable to the crack closure under increasing confining pressure.The subsequent permeability increase results from the development of microcracks when shear stress goes beyond the CI threshold value.This rapid increase continues until the peak strength is reached.At the post-failure stage,the evolution of permeability is found to be complicated by either decreasing or increasing trends with further axial strain.The observed permeability reduction can be attributed to grain crushing and pore collapse,which are not included in the current modeling.

Various permeability means are evaluated to assess the stress induced heterogeneity.The arithmetic and harmonic means of the permeability are respectively given as(Selvaduraiand Selvadurai,2014):

The geometric mean of the permeability is

or

whereViis the volume of zoneiandkiis its intrinsic permeability.According to a previous study(Selvadurai and Selvadurai,2014),the effective permeability is believed to be equivalent tokg,and ranges betweenkaandkhas

It has been reported that for Indiana limestone with natural heterogeneity in permeability,the geometric mean value appears to be representative of the effective permeability(Selvadurai and Selvadurai,2014).The above authors successfully verified that the geometric mean is a good proxy as a homogeneous material property to the experimentally measured heterogeneous distribution of permeability(Selvadurai and Selvadurai,2014).It is noted that no evidence of hydraulic anisotropy or fractures is considered in that study.Therefore,we computed both the arithmetic and geometric means of the simulated permeability to assess the impact of nonlocal deformation on overall variation in permeability.

Fig.10.Damage for specimens at different foliation angles ofβ=0°(left)andβ=90°(right):(a)Effective plastic strain,and(b)Tensile damage zone(1 indicates the damaged zones,and 0 indicates the undamaged zones).

Fig.11b and c shows the comparison between these two variables against the experimental data and the estimated effective permeability from the simulated pulse decay curve by the Brace equation(Brace et al.,1968).It is found that the harmonic mean can well reproduce the results of pulse decay tests when deformation is comparatively uniform,and all three means of permeability are consistent with each other.Once nonlocal deformation is formed,both the arithmetic and geometric means cannot represent the rapidly evolving heterogeneity anymore (Hamzehpourand Khazaei,2016).The harmonic mean of permeability is the closest proxy to the estimated permeability by pulse decay method.

Fig.11.Simulated and measured pulse decay curves for rock under different stages of triaxial test:(a)Temporal variation(β =90°),(b)Permeability evolution with axial strain atβ =90°,and(c)Permeability evolution with axial strain atβ =0°.Scattered dots are the experimental data and the lines are the simulated results.

Therefore,the pulse decay test,either in the form of experimental or numerical simulation,is highly recommended to assess the resulting permeability variation at the post-failure stage.This is consistent with the observation of Masihi et al.(2016)where a percolation concept was adopted to estimate the effective permeability of heterogeneous porous media with a wide distribution of local permeability.A power law and a threshold value of permeability were proposed by Masihi et al.(2016)to correlate the geometricmean with the effective permeability.Similarly,our permeability updating function also involves a power law of plastic strain and a threshold value of plastic strain,which also shows very good agreement with the permeability estimated by percolation based pulse pressure decay method.

Figs.12-15 show the multi-slice cross-sectional plotting of the evolution of permeability and effective plastic strain for Cobourg limestone specimens tested for different bedding orientations.It is noted that boundary conditions affect the damage extent and thus the permeability distribution.A less permeable boundary layer is observed when horizontal deformation is constrained at the bottom boundary.The friction between load pedestal and rock specimen may act as a horizontal constraint.Therefore,the measured permeability by pulse decay method applied on the rock-pedestal interface may somewhat underestimate the volumetrically averaged value,which can be clearly demonstrated in the contour plotting of the volumetric distribution of the damage permeability in Fig.12.

4.Modeling the long-term behavior

The behavior of the Cobourg limestone changes with time.As discussed by Paraskevopoulou et al.(2017),the time-dependent behavior is due to a combination of many physico-chemical processes that might include crack initiation and propagation and physico-chemical alterations at the grain contact levels that can result in strength degradation.The actual physico-chemical processes and the scale at which those processes operate are complex,and are the currently active area of research in micro-mechanics(Blaisonneau et al.,2016;Firme et al.,2016;Chen et al.,2017;Lu and Wang,2017;Wei et al.,2017).From a phenomenological viewpoint,two common laboratory tests that show evidence of time-dependent behavior are creep tests and relaxation tests.Herein,we use creep and relaxation tests on Jura limestone from Paraskevopoulou et al.(2017)in order to extend the constitutive relationships described previously to include time-dependent effects.Test data reported by Paraskevopoulou et al.(2017)confirmed that the time-strength degradation characteristics of the Cobourg and Jura limestones are similar.The model for long-term behavior is an extension of the short-term model,using exactly the same assumptions and parameters.However,time-dependency was taken into account by the inclusion of elasto-viscosity and time degradation of the strength parameters as described next.The adoption of this strength degradation functional relationship,combined with a simple viscoelastic model,satisfactorily reproduces the experimental data from creep tests as discussed in this section.

4.1.Visco-elasticity

The stress tensor and strain tensor can both be decomposed into volumetric and deviatoric components:

where σdand εdevare the deviatoric stress and strain vectors,respectively;p and εvolare the mean stress and volumetric strain vectors,respectively,and can be written as

For an elastic material,σ can be expressed as a function of ε by the mean and deviatoric components.For example,the isotropic elastic material obeys the following relationship:

whereKandGare respectively the bulk and shear moduli,which are scalars for an isotropic material,but tensors for an anisotropic material.

For a visco-elastic material,the deviatoric stress is dependent not only on the deviatoric strain but also on its time variations.The deviatoric stress is usually written in an integral form as follows(Simo and Hughes,1998):

Fig.12.Contour plotting of the simulated permeability(log10k)for Cobourg limestone(β =90°)at different stages of triaxial test when pulse decay tests were undertaken.The stages are shown at increasing load levels as indicated by the star-shaped points shown in Fig.9.

Fig.13.Contour plotting of effective plastic strain for Cobourg limestone(β =90°)at different stages of triaxial test.The stages are shown at increasing load levels as indicated by the star-shaped points shown in Fig.9.

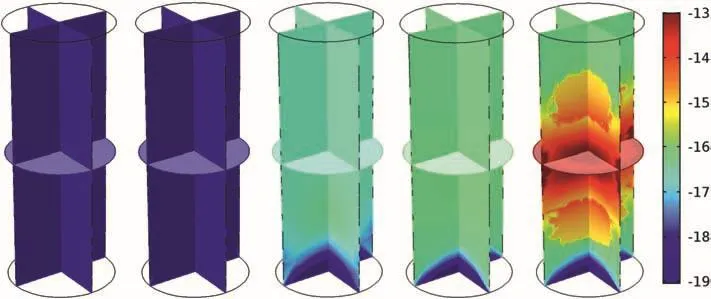
Fig.14.Contour plotting of the simulated permeability(log10k)for Cobourg limestone(β =0°)at different stages of triaxial test.The stages are shown at increasing load levels as indicated by the star-shaped points shown in Fig.9.

Fig.15.Contour plotting of effective plastic strain for Cobourg limestone(β =0°)at different stages of triaxial test.The stages are shown at increasing load levels as indicated by the star-shaped points shown in Fig.9.

wheret′is the time since loading is applied;and Γ(t)is a relaxation function,which can be approximated by a Prony series:

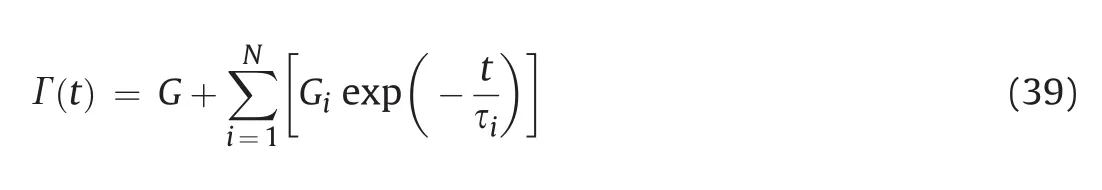
whereNis the total number of viscous branches;Giis the shear modulus of thei-th component branch;andτis the relaxation time as a function of viscosity(η)and shear modulus(G),i.e.τ= η/G.

A simple rheological model,i.e.the simplified general Maxwell model(also known as the standard linear solid(SLS)model)that consists of a spring and dashpot in sequence as shown in Fig.16,was implemented in the study of the rheological behavior of the Cobourg limestone.It is assumed that viscosity only influences the deviatoric components of stress and strain,as is the common assumption adopted in geomechanics.Viscosity under hydrostatic loading is rarely measured in the laboratory and is often poorly defined in the literature(Li et al.,2017).For these reasons,the authors adopted the simplifying assumption that viscosity is solely dependent on the deviatoric component of stress.

As only one viscous branch is considered,the integral deviatoric stress can be rewritten as

whereG1is the shear modulus of the viscous branch,andτ1is the relevant relaxation time.Eq.(40)can be reduced to another form in the absence of viscosity,i.e.τ1=0:

which suggests that the total stress is imposed solely onto the bulk elastic material when the viscosity diminishes.

Fig.16.Schematic diagrams showing(a)the visco-elasto-plastic model and(b)the standard linear solid model.

As shown in Fig.16,the total deviatoric stressσdequals the sum of both the bulk stress and the viscous stress(σq)in the form of

The stress on the spring-dashpot branch takes the following form:

where q1is the shear strain tensor of the viscous branch;η1and γ1are the viscosity and the viscous strain tensor of the dashpot,respectively;and˙γ1is the time derivative.

The above equation gives rise to the following formula:

The total deviatoric elastic strain thus consists of two parts:(1)the viscous strainγ1that is induced by the dashpot deformation,and(2)the elastic strain q1that is attributed to the spring.We then have

The viscous strains are then defined by the following equations:

4.2.Determination of the viscoelastic constants

In absence of plastic strain,the constitutive equation for viscoelasto-plasticity can be reduced to the SLS model.As shown in Fig.16,an elastic spring is placed in parallel with a series of springs and dashpots.Rearranging the constitutive equations for the SLS model by eliminatingγ1and q1leads to the following relationship that is merely dependent on total strain and total deviatoric stress:

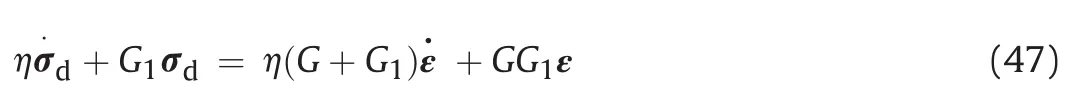
In order to extract the rheological parameters for the Maxwell model from experimental results,it is important to analyze the above formula using the analytical solutions for the relaxation modulus and creep compliance.

In a stress relaxation test,a constant strain ε0is applied while the time-dependent stress variation is monitored.Using Laplace transform,the relaxation modulus(Erel)is given as(Gutierrez-Lemini,2014):

Similarly,the creep compliance(CM)of the Maxwell model can be derived as

These formulae enable the direct parameterization of the experimental results on relaxation or creep tests,which are both exponential functions of time,and can be numerically estimated by optimizing techniques,e.g.least-square algorithm.

4.3.Time-dependent yield criterion

Mechanical damage to intact rock is cumulative in terms of microcrack initiation and acoustic emission.The long-term rheological behavior and the stability of rock mass are dependent on the extent of the mechanical damage as well as the time history.According to experimental observation of rocks under creep conditions,cumulative damage to rock occurs when the deviatoric stress is maintained at a level higher than the CI threshold,which leads to an abrupt failure after a period of time.With respect to the rheological behavior,the strain rate varies with elapsed time.A typical second phase of creep takes place in terms of steady state strain,and ends with a minimum value in strain rate prior to an accelerated strain rate that is characteristic of the creep failure stage.

Assuming that damage is associated with deviatoric stress,then the time required to reach failure(tF)may be given as a function of stress ratio σd/ℑ,where ℑ is the short-term compressive strength.No long-duration test data are available for the Cobourg limestone at the time this paper was prepared.Test data on Jura limestone,a rock that presents many similarities with the Cobourg limestone,obtained by Paraskevopoulou et al.(2017),were used to derive the empirical relationship for the time-degradation of strength as follows:

Eq.(50)means that when a deviatoric stress equal to ℑ is applied,the sample fails instantaneously.However,if a smaller stress is applied,delayed failure will occur at timetF.Under unconfined test conditions,ℑ is equal to UCS and corresponds to timet≈0.Fig.17 shows the test data and the best- fitting with Eq.(50).

In the elasto-plastic framework,the peak strength can be assumed to be degrading with time.With ℑ as the short-term peak strength,andqfas the temporal peak strength,the damage factorωtcan be defined as

withtas the elapsed time since beginning of stress loading.It can be easily demonstrated that at the moment when the sample fails under creep loading conditions,i.e.t=tF,the temporal peak strengthqfequals the applied deviatoric stressσd.Therefore,the function of timef(t)is written as

Fig.17.Experimental observation of time-to-failure criterion for Jura limestone(left)and the transformed data with best- fitted expression(right)(data from Paraskevopoulou et al.,2017).

For Mohr-Coulomb strength,the deviatoric stresses are related to cohesion and friction as

where superscript 0 indicates the short-term strength parameters(i.e.t≈0).Therefore,the internal cohesion takes the form of

Eliminatingσ1in terms ofqfand σ3,we have

Taking into account triaxial test conditions with confining pressure maintained as constant,by inserting ℑ into the above formula and eliminatingσ01,we have

4.4.Modeling the rheological tests on Jura limestone

Stress decay of Jura limestone during the uniaxial unconfined relaxation test is shown in Fig.18.The measured stress was normalised against the peak strength,and plotted with elapsed time.The stress relaxation compliance formula for the SLS model was applied to best- fitting the test data.The obtained parameters as shown in Fig.19 include the elastic shear modulus(G1)and relaxation time(τ)of the Maxwell viscoelastic branch.The best fitted empirical relationship for the SLS model parameters can be written as

It is noted that the relaxation time,which represents the viscosity of the rock sample,depends uniquely on the stress level.In order to simplify the application in modeling,the damage factorωtwas adopted to represent the stress ratio.Therefore,the above equation turns into another expression:

A finite element model integrating the visco-elasto-plastic model as described above was developed to study the stress relaxation of Jura limestone.Fig.20 shows the comparison between simulated and observed results on stress evolution during relaxation tests.Fig.21 shows the simulation results of creep tests at different stress levels,where the time of failure is indicated by a steep acceleration of the strain rate during creep tests.The time of failure is reported in Fig.22 and compared to the experimental data.The model is found to reproduce the test data with a high degree of agreement.The time-to-failure parameter is dependent on the applied shear loading.

Fig.18.Stress relaxation of Jura limestone with time under various deviatoric loadings.

Fig.19.SLS model parameters versus normalised stress ratio and the regression formula.

Fig.22.Comparison of strength degradation (normalised with transient peak strength)with time as observed from experiments and modeled by finite element method.

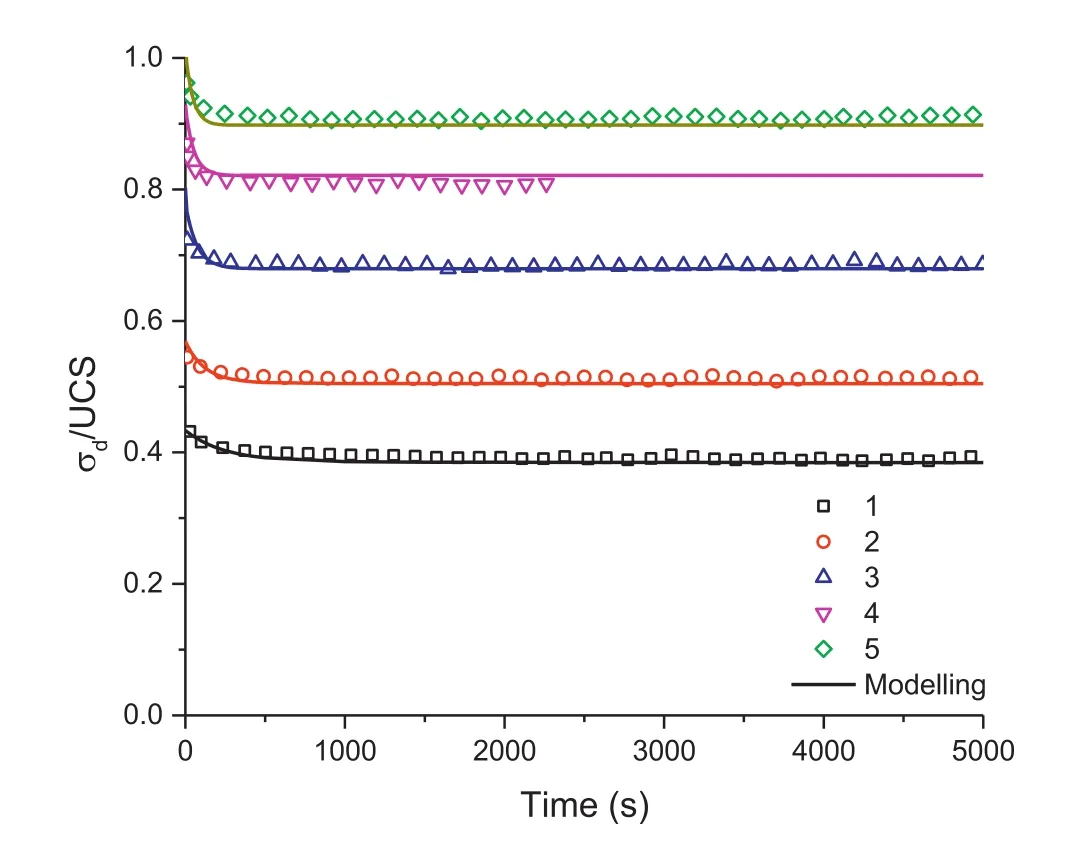
Fig.20.Modeled stress relaxation curves(solid lines)versus experimental measurement(scattered dots).

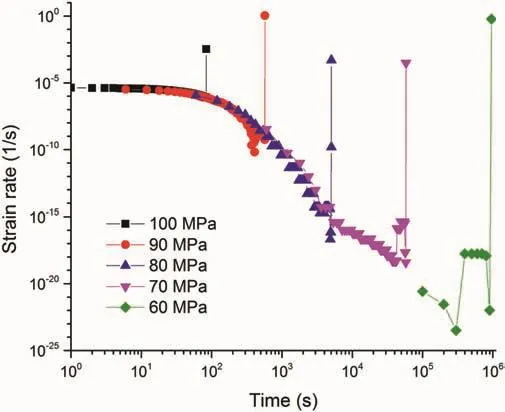
Fig.21.Simulation of creep tests at different stress levels.A steep increase in the strain rate indicates failure of the sample.

5.Conclusions

Excavation damage in the near- field of a DGR has been found to be accompanied by an increase in permeability from most field studies.The EDZ therefore might constitute preferential pathways for radionuclide transport,and must be taken into account in the design and safety assessment of the repository.In practice,the two most important parameters of the EDZ would be its extent and its bulk permeability.The safety analyst and the repository designer would use conservative estimates in order to respectively perform safety assessment of the DGR and design mitigation measures.The verification that those estimates are indeed conservative is an iterative process,through ongoing research throughout the life cycle of the DGR in order to improve the understanding of the processes leading to the EDZ formation,evolution,and its characteristics.The present study has provided some further understanding on the interrelationship between damage and permeability for the Cobourg limestone,which is a candidate host rock formation in Canada.This study examined both the short-and long-term hydro-mechanical behavior of the Cobourg limestone based on macroscopic observations from laboratory triaxial tests,with or without permeability measurements.

In this paper,we summarized the results of laboratory triaxial tests on Cobourg limestone with the measurement of permeability evolution.A mathematical model is developed to interpret the hydro-mechanical behavior of the Cobourg limestone during the tests.The model is based on the classical theory of poromechanics in order to couple the hydraulic and mechanical processes.The constitutive equation for the stress-strain behavior is developed within the strain-hardening and softening elasto-plastic framework,taking into account the inherent anisotropy of the rock due to bedding.Furthermore,a nonlocal hardening parameter is used in order to regularise the governing equation of equilibrium,and simulate strain localization.The ability of the model to reproduce the main physics was shown in the paper.It shows excellent agreement with the experimental stress-strain curves,is capable of reproducing the effect of loading orientation with respect to the bedding direction,and can fairly reproduce the shapes and orientation of the failure zones.The model was also used to simulate pressure pulse tests performed at different stages of triaxial loadings with very good agreement.It was shown that increased loading created heterogeneous damage and permeability in the sample.The harmonic mean of the permeability field is found to be the best proxy to represent the effective permeability of the rock sample at all stages of loading.The model indicates that damage results in an increase in the effective permeability by up to three orders of magnitude after the peak strength.This is consistent with most of the experimental results.However,in a few cases,the experimental results from the pulse tests indicate a post-peak decrease in permeability which might be attributed to gouge formation and boundary effects that we cannot simulate at present.Using creep and relaxation data on a similar limestone,the Jura limestone,we included viscosity and strength degradation in order to include the time-dependent behavior of such a rock type.

Many assumptions in macroscopic models,including the one presented here,need to be confirmed and verified.Such confirmation could be performed through experimental and theoretical studies of the physico-chemical processes at the microscale to understand how those processes influence the macroscale hydromechanical behavior of the rock.Future research should include the following aspects:

(1)Anisotropy is due to stratification resulting from the sedimentation process.Heterogeneity originates from the interspersed fabric of a calcite,dolomite-rich limestone nodules separated by argillaceous wisps and inclusions.The percentage of argillaceous inclusions creates an apparent scale effect,with larger samples exhibiting higher strength since they demonstrate a more homogeneous nature than the smaller ones.The relationship between microstructure,anisotropy,heterogeneity and scale effects should therefore be better understood.

(2)The permeability increases by up to four orders of magnitude at the residual stress level,after failure.The high post-peak permeability is due to the presence of cracks that form preferentially in the weaker argillaceous inclusions.The influence of post-peak cracking on the bulk hydro-mechanical behavior needs also to be better understood.

(3)The long-term strength degradation characteristics of the Cobourg limestone complemented with data from the Jura limestone were determined from tests with durations of the order of months to years.The reference time frame for geological repositories is of the order of up to one million years.The validity of the extrapolation from the former to the latter time frame needs to be supported by more fundamental approaches that look at the basic phenomena occurring at the microscale.

Conflicts of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant support for this work that could have influenced its outcome.

Acknowledgments

The authors sincerely thank the Canadian Nuclear Safety Commission for funding this project.