基于多图像先验知识的噪声水平评估算法

徐少平 曾小霞 唐祎玲 江顺亮

(南昌大学信息工程学院 南昌 330031)

现有已提出的大多数图像降噪算法实际上属于非盲降噪算法(non-blind denoising algorithm)[1-6].在实际使用中，这些非盲降噪算法只有在获得关于噪声图像准确的噪声水平值(即高斯噪声模型中的方差)作为入口参数后才能得到比较好的降噪效果.因此，以获得噪声图像的噪声水平值为目标的噪声水平评估(noise level estimation, NLE)算法被相继提出来[7-13].已提出的NLE算法绝大多数都是属于所谓的基于单图像噪声水平评估 (single-image based noise level estimation, SNLE)的类型，仅仅依据噪声图像本身评估图像中的噪声水平值.早期，Immerkaer[14]提出先用掩模对图像进行滤波得到各个像素点在局部邻域内的方差，然后以所有像素点上求得方差的平均值作为整个图像噪声水平估计值.以Immerkaer算法为代表的基于对整个图像执行滤波操作实现的NLE算法主要特点是其执行速度非常快，然而在很多情况下所给估计值的准确性却不高，尤其是对于具有复杂纹理内容的图像和受中、高噪声水平干扰的图像[15].为获得更高的预测准确率，近年来研究者们逐渐开始在图块(image patches)粒度上研究噪声水平评估问题.2013年,Liu等人[16]提出了一种被称为基于弱纹理图块(weak-textured patches)的噪声水平评估算法.该算法基于梯度和统计分析的方法从噪声图像中选择出弱纹理图块，使用主成分分析(principal component analysis， PCA)计算弱纹理图像块协方差矩阵的最小特征值并将它作为噪声水平值的估计.2015年，Chen等人[17]从理论上推导出了噪声图像中图块的协方差矩阵若干特征值与噪声水平值之间的计算关系，依赖满足特定条件的若干个特征值估计图像中的噪声水平值.该算法在利用若干特征值导出噪声水平值的过程中仍然采用迭代方式选择所需要的特征值.类似地，Huang等人[18]基于纹理特征值分析，先判断局部图像块的光滑程度来选择弱纹理图像块，再对选择出来的这些图像块进行特征值分析.选择图块的过程是以迭代的方法完成的.上述这些基于图块粒度实现的NLE算法最大特点就是预测准确性比较高，但是由于在内部实现中大多采用迭代方式进行，计算效率比较低.上述NLE算法的工作原理在某种意义上讲是将噪声图像中的噪声信号和图像信号分离，然后基于噪声信号部分估计图像的噪声水平值.这种方法在实现的过程具有一定的难度，计算复杂度高.与利用噪声与图像信号分离的实现策略不同，还有一类算法试图通过利用图像受到噪声干扰后所表现出的规律性变化实现对噪声水平值的估计.例如Zoran等人[19]通过分析图像DCT变换后的系数发现噪声会导致图像Kurtosis值有规律变化，并根据这种现象提出了一种基于Kurtosis值尺度不变性的噪声水平评估算法.该算法在一定程度上改善了图像噪声估计的效果，但是它是通过寻找目标函数最优值的方法实现的，计算效率比较低且在高水平噪声条件下存在寻优失败的可能.在此基础上，Dong等人[13]利用自然图像带通域里的Kurtosis值的不变性和分段平稳性，提出一种新的噪声水平估计方法，能够有效地估计各种类型的噪声，在非高斯噪声下表现出色.此外，Khmag等人[12]根据图像块梯度的统计特性，从噪声图像中去除高频分量，筛选出低秩图块(low-rank patches)，再使用PCA分析技术进行噪声水平评估.虽然上述3个NLE算法基于图像统计特性实现了噪声水平评估，但仅是在单幅噪声图像上进行的.

虽然近几年提出的SNLE算法都取得了一定程度上的成功，但是仍有2个问题亟待解决:

1) 抗干扰能力弱.现有的SNLE算法均假设噪声图像中噪声为纯高斯噪声，实际应用中碰到的高斯噪声往往混合有少量脉冲或者泊松等类型的噪声.SNLE算法对此情况的处理不够鲁棒，对高斯噪声水平值的估计往往会出现较大偏差，从而影响后续相应处理算法的性能.

2) 计算效率低.由于SNLE算法仅有噪声图像本身的信息可以利用，为此很多SNLE算法设计了各种复杂的处理流程从而保证估计出准确的噪声水平值，但是复杂的处理过程也导致这类算法的执行效率严重下降.而NLE算法作为众多图像处理工作的前置模块，不但需要提供关于噪声水平值准确的估计，更需要在尽可能少的时间内完成，以避免影响后继图像处理算法的整体效率.

鉴于SNLE算法存在的问题，近年来在噪声水平估计及相关领域所完成的一些工作表明可以基于多幅图像开展这方面的工作.例如在文献[20]中，Chen等人提出了一种基于多图像的非局部均值估计(non-local means， NLM)的降噪算法.NLM算法[5]是非常成功的一类经典降噪算法，它降噪效果好坏的关键在于能否找到足够多的与噪声像素点具有类似图块结构的像素点进行降噪.Chen算法与经典的NLM算法不同，它将搜索类似图块结构的范围扩展到待降噪图像自身之外的其他相关图像中，故它能利用更多的冗余信息实现更好的降噪效果；在文献[21]中Shih等人提出依据多幅具有相同图像内容的不同噪声水平图像之间的概率分布来实现一种NLE算法.该算法的主要缺陷在于它仅能处理人脸图像集合，并且图像之间需要根据人脸特征点进行对齐，故应用范围有限，但Shih等人的工作表明利用多个图像信息进行噪声水平值估计是可行的；最近在文献[2]中笔者提出了一种利用图像在小波变换域上所蕴含的自然场景统计(natural scene statistics， NSS)规律，通过提取特征矢量以刻画图像中的噪声水平值，然后利用支持向量回归(support vector regression， SVR)技术在一组具有广泛代表性的自然噪声图像训练集合上通过训练获得图像噪声水平估计的预测模型(即NLE算法).该算法最大的特点就是它的预测性能已经不受图像内容影响，可以是任意的图像.然而，它是基于SVR训练预测模型的实现策略，可扩展性较差.一旦图像受到除高斯噪声外的其他噪声干扰，就有可能失败.

为进一步改进文献[2]中的工作，本文提出了一种基于先验知识的多图像噪声水平评估(multi-image based noise level estimation， MNLE)算法.MNLE算法的创新思想来源于：图像经过适当的预处理后，可以提取出若干个具有规律性的统计值，而且这些统计值在图像受到噪声干扰后仍然保持有规律的偏移.换句话来说，这些特征值与图像噪声水平值之间具有极强的相关性，本文将这些统计值称之为噪声水平感知特征(noise level-aware feature, NLF).所提出的MNLE算法正是利用多幅与待评价噪声图像噪声水平感知特征矢量近似的样本图像(已经标定了噪声水平值)，以它们之间的相似程度作为加权系数，用加权均值法(weighted average approach)实现对待评价噪声图像噪声水平值合理的估计.MNLE算法的抗干扰能力很好，只要样本库中存在类似的图像就可进行噪声水平估计.另外，MNLE算法执行时间效率非常高，主要归功于3个方面：

1) 在进行噪声水平值评估时仅仅需要在事先建立好的样本库中依据特征矢量完成查找操作，不用基于图像本身进行比较.

2) 直接在空域上提取噪声图像的噪声水平感知特征非常节省时间.

3) 采用查找表检索的方法提高特征矢量之间比较的计算效率.

通过上述改进，MNLE算法较经典的SNLE算法具有更高的执行效率和预测准确性，更符合各类图像处理应用的需求.

1 现有问题

目前，大多数SNLE噪声水平评估算法通常都假定图像中噪声属于高斯噪声类型.然而实际应用中，高斯噪声往往很少单纯存在，它常常伴有脉冲或者泊松等其他类型噪声.如表1所示，利用具有代表性的Immerkaer算法[14]、Zoran等人算法[19]、Yang等人算法[22]、Liu等人算法[16]和Chen等人[17]算法对各种高斯噪声水平值的Lena噪声图像(均伴有5%脉冲噪声)进行噪声水平值估计.可以看出，在脉冲噪声的干扰下，现有的SNLE算法评估的结果与真实值之间都存在极大的偏差，尤其是低水平和高水平高斯噪声条件下.出现这种情况的原因在于现有算法在设计的时候均假设图像中的噪声为纯高斯噪声，对可能混入其他的噪声干扰没有考虑.然而脉冲噪声与高斯噪声对图像内容的影响是完全不同的方式，现有的SNLE算法对这种情况缺乏应对处理能力，即便是图像中仅混入了5%这样非常低的脉冲噪声都会对最终的估计结果产生很大影响.

Table 1 Estimation Results Obtained with Different NLE Algorithm in the Case of Mixed Noise表1 在伴有脉冲噪声情况下各NLE算法的估计结果

另外一方面,现有预测准确性比较好的SNLE算法(例如Liu算法)往往执行时间都比较长(参考表8中的数据).其主要原因在于Liu算法仅依据噪声图像本身进行噪声水平值估计.Liu算法定义了所谓弱纹理图块(weak-textured patches)的选择条件，试图从噪声图像中找出图像内容相对比较平滑的区域进行噪声水平值估计，然而这个选择条件却要依赖噪声水平值这个需要估计的值来确定，这是一个典型的“鸡和蛋”问题(chicken-and-egg problem).因此，Liu算法不得不采用迭代逼近的方式进行求解，导致整个算法的执行时间比较长[16].一般地，NLE算法作为众多图像处理算法的预处理模块，其执行时间过长，将严重降低整体的执行效率.因此，SNLE算法中存在的上述“鸡和蛋”问题有待于进一步的解决.

2 MNLE算法

2.1 基本思想与实现策略

对自然图像的像素点亮度值分布情况的相关研究表明[23]：自然图像经过适当处理后能够从中提取出一些非常稳定统计值(与图像内容相关性不大，而与图像噪声水平密切相关)，而且一旦自然图像受到噪声的干扰，这些统计值也会发生有规律的偏移，因此可以利用这些统计值作为描述噪声水平值的特征值.为此，本文提出一种基于多图像先验知识的噪声水平评估的MNLE算法，试图实现对噪声水平值快速而鲁棒的预测，解决SNLE算法存在的抗干扰能力差和执行效率低的问题.MNLE算法采用2阶段实现，在数据准备阶段，在具有广泛代表性且未受噪声干扰图像集合上添加具有不同噪声水平值的噪声构建失真图像集合，并在空域上提取失真图像中的若干自然统计特征值构成刻画噪声水平值高低的噪声水平感知特征矢量,然后，利用失真图像上所提取的特征矢量与其对应的噪声水平值构成样本库；在评价阶段，依赖于在样本库检索出若干与待评价图像类似的特征矢量及它们所对应的噪声水平值用加权均值法实现噪声水平值的评估.下文就MNLE算法各个步骤具体实现细节进行详细介绍.

2.2 噪声水平感知特征提取

原始无失真的自然图像中像素点亮度值变化的规律性不强，如图1(c)所示.但是经过适当预处理后却可以从中提取许多有规律的统计数据，如图1(d)所示.本文为提高效率，预处理工作在空域内完成.具体地，给定一个图像I，预处理后的图像为

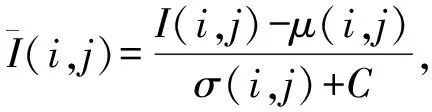
(1)

其中，i∈1,2,…,M，j∈1,2,…,N是图像I的像素位置，M和N分别表示图像的宽和高，C=1是为了保证稳定性而设置的常量值.μ(i,j)和σ(i,j)分别由下面计算方法得到：

(2)

(3)

其中，ω={ωk,l|k=-K,-K+1，…，0，…,K-1，K,l=-L,-L+1，…，0，…，L-1,L}是一个对称高斯滤波器.

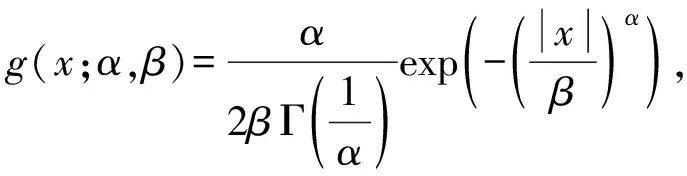
(4)

其中，Γ(·)是关于伽马的函数，

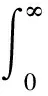
(5)

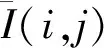
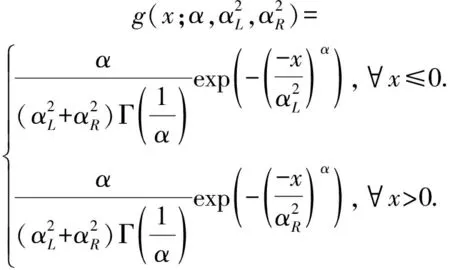
(6)

AGGD的均值定义为

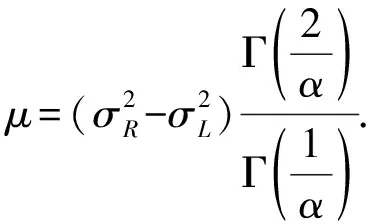
(7)

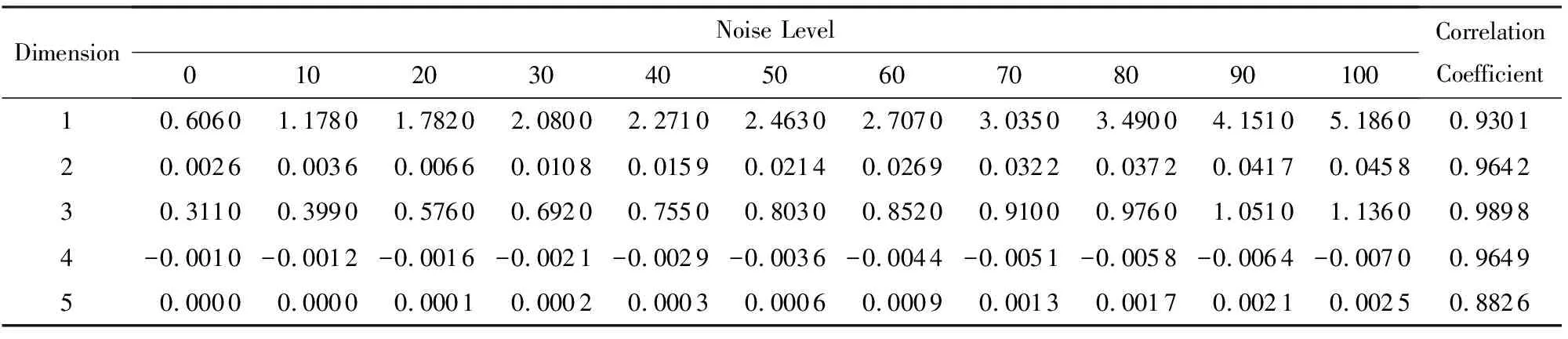
Table 2 Eigenvalues Extracted from Barbara Image at Different Noise Levels表2 在不同噪声水平下从Barbara图像上提取的特征值

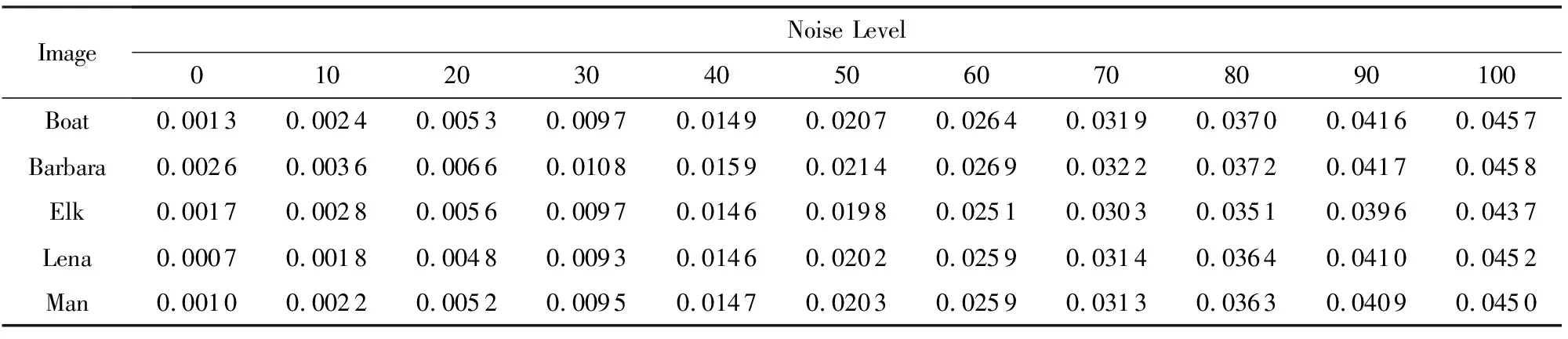
Table 3 The Second Dimension Eigenvalue Extracted from Different Noisy Images at Different Noise Levels表3 在不同噪声水平下从各噪声图像上提取的第2维特征值

2.3 噪声水平感知特征相关性分析

为了验证基于GGD和AGGD模型提取的噪声水平感知特征值是否对噪声水平值敏感(验证它们之间的相关性)，以Barbara图像为例，对其施加不同噪声水平值的噪声，然后提取各噪声图像的特征矢量进行分析，结果如表2所示,限于篇幅，仅列18维特征值中的前5维特征.可以看出：随着噪声水平的增大，各维上的特征值都相应地发生有规律性变化，存在显著的相关性.表2中最后1列列出了各行特征值与相应的噪声水平值之间的相关系数都在0.88以上，甚至有的高达0.98，这说明基于GGD和AGGD模型提取的特征值的变化与噪声水平值变化都是密切相关的；表3中的数据是5幅不同内容的图像在不同高斯噪声水平值下提取的第2维特征值列表(限于篇幅，仅列第2维数据).可以看出，在大多情况下，对于相同的噪声水平值，从不同噪声图像上提取的特征值非常近似，这说明本文所提出的噪声水平感知特征对某一特定噪声水平值的反映是相对稳定的.总之，从表2、表3中可以看出，本文所提出的噪声水平感知特征值的变化能够反映噪声水平值高低，它们之间具有高度的相关性.对于高斯噪声中伴有脉冲噪声或者伴有泊松噪声的情况，总体与表2、表3情况类似，这里不再列出.总之，本文所提出的噪声水平感知特征值与图像内容无关，而仅与图像中的噪声水平大小相关.

2.4 噪声水平值估计

为了简化加权均值法实现细节的描述，假设已经运用上文所提出的特征提取方法获得了n幅失真图像的特征矢量{x1,x2,…,xn}⊂X，其中，每一个样本矢量xi均已经标定了其对应的噪声水平值σi.对于某个待评估的噪声图像，其噪声水平感知特征矢量用y表示，则它的噪声水平值可进行估计为

(8)

其中，w(y,xi)是权重函数，它的大小依赖于特征矢量y与样本库中xi的矢量距离(相似程度).具体实现上，权重函数可以定义为

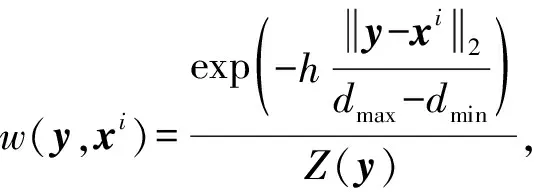
(9)

(10)

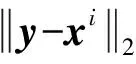
通常，在噪声图像集合上提取完图像噪声水平感知特征矢量(其对应的噪声水平值已知)后，完全可以采用SVR等各种回归分析技术训练预测模型将特征矢量映射为相应的噪声水平值.本文没有采用常规方法而是基于加权均值法实现对噪声水平值的估计，其主要的原因在于基于SVR等方法构建的预测模型依赖于训练集中全体数据，一旦有新类型噪声图像需要预测，就必须重新训练模型.随着各种噪声类型增加以及复杂纹理内容的图像的出现，其所构造的非线性映射预测模型的泛化能力会越来越差，预测准确性会越来越不理想，故基于SVR构建的预测模型可扩展能力较差.本文所提出的MNLE算法的设计目标是除了实现纯高斯噪声的预测外，还能够处理高斯噪声中伴有脉冲噪声或者泊松噪声条件下的预测，只要在样本库中加入相应的样本即可，无需重新训练.为此，提出了基于加权均值法的预测方法.采用加权均值法预测噪声水平值，只要样本库中存在少量与待评价的图像类似的图像，该预测模型就可以工作，鲁棒性和准确性都比较好.

3 实验与分析

3.1 实验配置以及相关参数设置

为了验证MNLE算法的评估效果，选择当前具有代表性的Immerkaer算法[14]、Zoran等人算法[19]、Yang等人算法[22]、Liu等人算法[16]和Chen等人算法[17]参与对比.算法运行的硬件平台为Intel CoreTMi7-6700 3.40 GHz CPU处理器、8 GMB内存、软件配置为Windows 7 操作系统、Matlab2014a.以文献[24]中使用的90幅图像和从互联网随机获得的10幅图像为基础构建样本数据库，对每幅图像添加101个不同等级的纯高斯噪声(噪声等级为0～100，步长为1)，并用提取它们的特征矢量，这些特征矢量与它们所对应的噪声水平值构成样本库.对于纯高斯噪声图像，数据库中保存了10 100条样本记录；此外，为了测试对伴有脉冲和泊松噪声的混合噪声的估计，在纯高斯失真图像的基础上添加5%的脉冲噪声；对于泊松噪声本文在纯高斯失真图像的基础上添加参数为γ=0.5，σu=0.5的泊松噪声(参数含义详见式(11)说明)，因此样本库中共有30 300条记录.测试图像集合主要包括BSD数据库[25]和各种文献中广泛使用的常用图像集合2个部分.

3.2 参数h的确定

在式(8)中，参数h控制了权重函数值的衰减速度，h的值越小，各个样本之间权重分配越平均；反之，权重越偏向于与待评估图像特征距离更小的样本.参数h对MNLE算法最后的评估结果有着重要的影响，目前通过理论分析来确定它的最优值尚有一定困难，需要考虑的影响因素较多.但是，可以根据在一些典型数据集合上的实际测试结果来确定大致合理的值.因此，选用BSD数据库[25]的100幅图像作为测试图像,其中一部分图像如图2所示，进行噪声水平评估实验.BSD数据库含有500幅图像，它原本是用来评价图像纹理分割效果的数据库，其图像纹理细节变化丰富，对于大多数NLE算法来说都是比较大的挑战，因此选用这些图像构成确定参数h值的测试图像集合能够保证图像具有广泛的代表性.有了这些测试图像后，对这些图像施加已知噪声水平的噪声，然后利用所提出的MNLE算法对这些噪声图像的噪声水平值进行预测，随后计算预测值与真值的均方根误差(root-mean-square error， RMSE) .

采用上述方法，在预测时使用不同的参数h值可获得一组均方根误差指标(均方根误差是反映预测准确性的统计性指标，它的数值越小，表明预测准确性越高)列在表4中.由表4可知，参数h的值取1.8～ 2.2之间时，在低、中、高噪声水平能够获得接近最优的预测准确率.综合考虑，本文将参数h的值定为2.0，下文所完成的实验数据都是在这种情况下获得的.

Fig. 2 Some images from BSD database for determining the optimal value of parameter h图2 用于确定最优参数h的部分图像(来自BSD数据库)

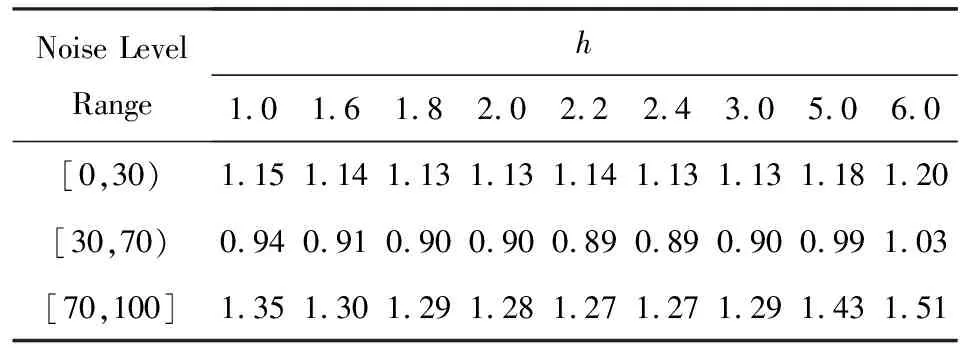
Table 4 The Influence of the Setting of Parameter h on theEstimation Performance

3.3 纯高斯噪声

3.3.1 预测准确性

1) 为了验证MNLE算法对高斯噪声图像的评估效果，对在各大文献中出现的常用图像进行了测试.如图3所示，这些图像包括了Airplane，Couple,Lena，Man，Peppers，Rapids，Ocean，Woman，Painted house，Sailing，它们在图像降噪、图像分割和图像质量评价方面等文献中被广泛作为基准测试图像.对这些无失真图像施加方差为10～100的高斯噪声.表5列出了各种评估算法对Woman图像在纯高斯失真条件下图像的评估结果(限于篇幅仅给出Woman图像).可以看出：对于低水平噪声，MNLE算法虽然不是最优的算法，但是预测准确性基本上都保持在前3名；而对于中、高水平的噪声，各参与比较的算法都存在越来越严重的欠估计(under-estimation)，而MNLE算法则取得最优的预测结果.表6是各个算法在10幅常用图像集合上在各个噪声等级下所预测结果与噪声水平真值之间的均方根误差.可以看出，在低水平噪声条件下MNLE算法虽不是最优，但是评估准确性进入前3名.随着噪声水平的提高，参与对比的算法评估效果越来越差，而MNLE算法则表现得非常稳定，一直处于排名第1的位置.

Fig. 3 Commonly used images in the literature图3 相关文献中常用图像所构成的测试集合

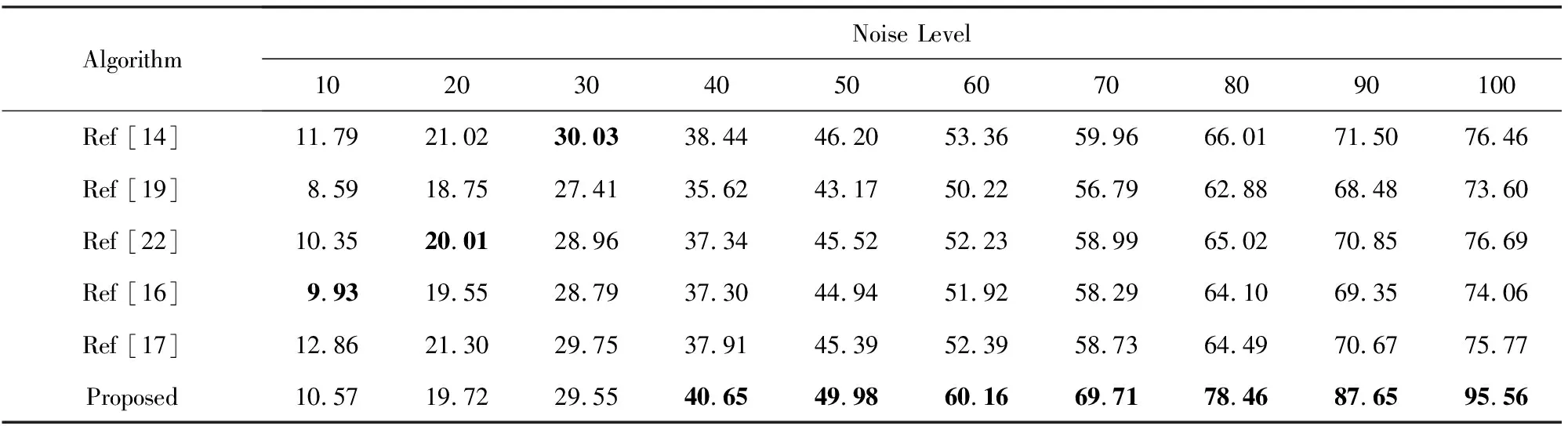
Table 5 Estimation Results Obtained with Different Algorithms on Woman Image at Different Noise Levels表5 各算法对Woman图像各个级别噪声的预测结果

Note: The best results are emphasized in boldface.

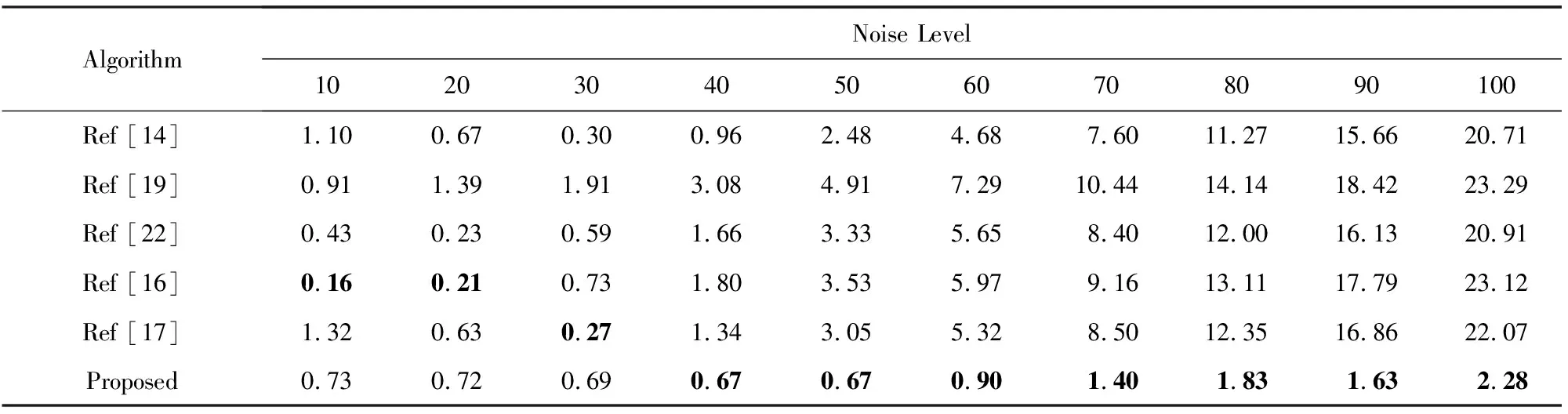
Table 6 RMSE Between Estimated Results and Ground Truths on Commonly Used Images表6 各算法在常用图像数据集合上预测结果与真值之间的均方根误差

Note: The best results are emphasized in boldface.

2) 为了进一步全面验证MNLE算法的评估效果，选用BSD图像集合中20张图像构成数据集进行测试(与之前确定参数h值所用的图像不重复).各个算法所预测结果与噪声水平真值之间的均方根误差列在表7中.从表7中的数据不难发现：各个算法的表现基本与在常用图像集合上类似，MNLE算法在低水平噪声下仍然进入了前3名，在中、高水平的噪声则全面超越所有参与比较的算法.综合来说，MNLE算法是参与比较的算法中预测准确性最为稳定的算法.

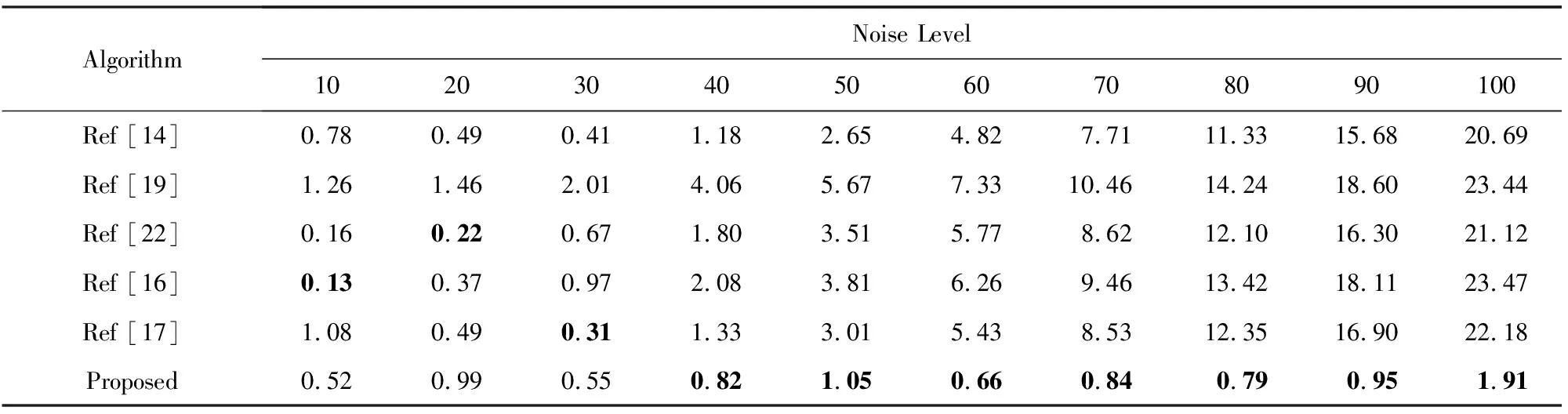
Table 7 RMSE Between Estimated Results and Ground Truths on Twenty Images from BSD Database表7 各算法在20幅BSD图像集合上预测结果与真值之间的均方根误差

Note: The best results are emphasized in boldface.

3.3.2 执行效率

预测准确性只是衡量NLE算法性能的一个方面.作为降噪等其他图像处理算法的前置模块，其执行效率是另外一个重要的衡量指标.为了比较各算法的执行效率，对不同噪声水平值的Lena图像(512×512)进行了10次评估，以10次执行时间的平均值作为最终参与比较的数据列在表8中.

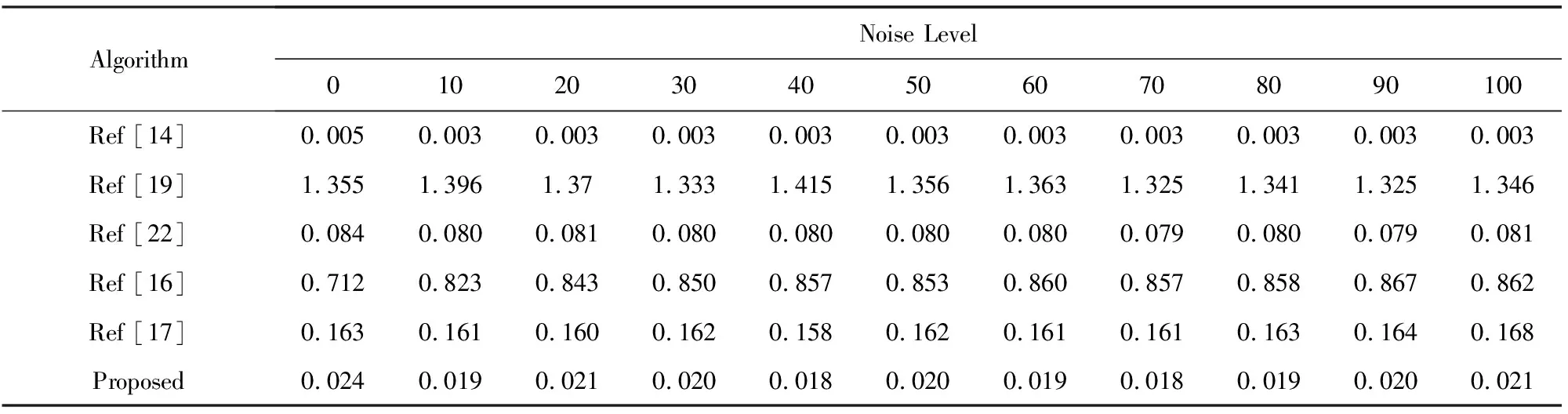
Table 8 Execution Time of Different NLE Algorithms表8 各个NLE算法执行时间的比较 s

由表8可知，在所有参与比较的算法中，MNLE算法对噪声的评估速度非常快,它仅比Immerkaer算法慢一些，非常适合作为各种算法的前置模块.MNLE算法之所以具有这样高的执行效率的原因在于3个方面：1)它完全在空域上提取统计特征值，没有转换到其他变化域的过程，这部分所需执行时间很少.2)噪声水平感知特征在构建样本数据库中已经建立完成.相对图像来说，样本库存储的是各个图像的噪声水平感知特征矢量，所需的内存其实非常少，评价时可以完全载入内存.在预测时，MNLE算法主要的计算代价是特征矢量之间的比较，而非图像之间的直接比较，所以计算速度非常快.3)利用查找表T加速检索样本库中特征矢量的速度.在构建样本库后，可以利用聚类算法(clustering algorithm)对样本库中噪声水平感知特征矢量进行分类，将样本库中噪声水平感知特征矢量按照矢量空间位置关系划分为N个子类.第i类的中心矢量(centroid)作为查找表中第i个目录T(i)，1≤i≤N.在检索时，先将待评价图像的特征矢量与查找表T中所有的目录中保存的中心矢量进行比较，找出与它距离最小的某个目录T(m);然后再与目录T(m)所代表第m类中所有的特征矢量比较.因此，这种基于查找表的检索方法，可以大大减少特征矢量之间的比较次数.需要特别说明的是：虽然Immerkaer算法在执行时间方面是所有算法中最快的，MNLE算法排名第2;然而由表6、表7中的数据表明Immerkaer算法在中、高噪声水平下预测效果很差，且抗噪声能力也很差.因此，MNLE算法在所有参与比较的算法中，在执行效率和预测准确性2个方面综合性能更优.

3.3.3 实际应用效果

为了验证MNLE算法的实际使用效果，将它应用到经典BM3D降噪算法中.分别比较BM3D算法使用真实的噪声水平值和使用MNLE算法估计的噪声水平值对常用图像集合进行降噪实验，将降噪后图像的峰值信噪比(peak signal-to-noise ratio, PSNR)、结构相似性度量(structural similarity index measurement, SSIM)[26]、特征相似性度量(feature similarity index measurement, FSIM)[27]指标平均值列在表9中.表9中的数据表明，MNLE算法估计的噪声水平值与使用真值的结果相差无几，这意味着使用MNLE算法的预测效果非常好.

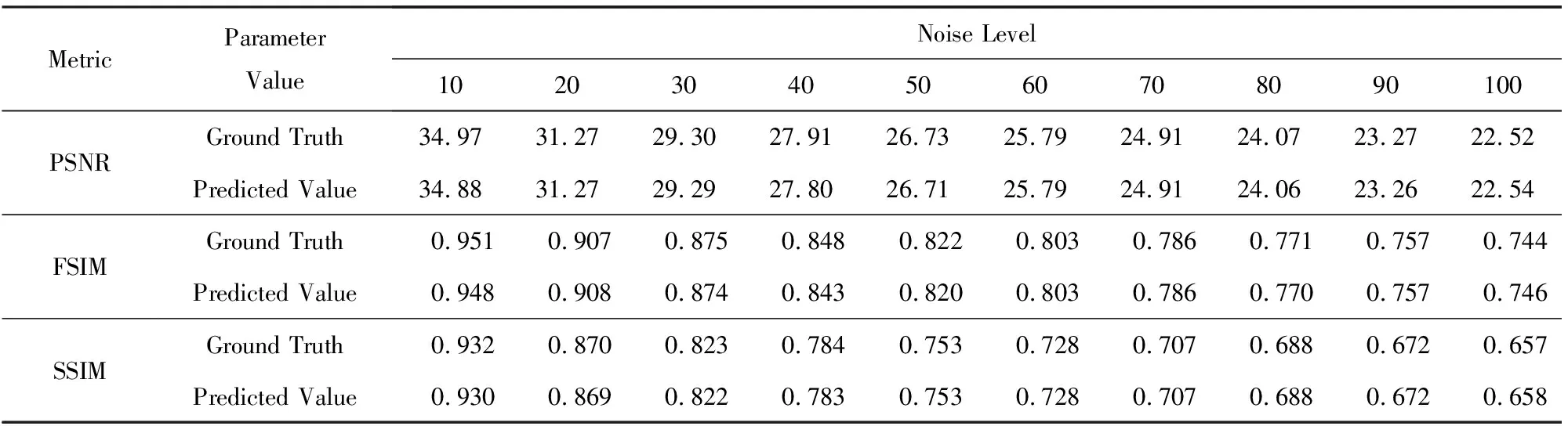
Table 9 Average Denoising Effects of the BM3D Algorithm Using Ground Truth and Estimated Noise Levels 表9 在常用图像集合上BM3D算法使用真值和估计值的平均降噪效果

3.4 混合噪声

3.4.1 伴有脉冲噪声

高斯噪声被广泛地用于图像降噪方面的研究中，但实际上，高斯噪声往往伴随脉冲噪声出现.为了验证各算法在混有其他类型噪声条件下是否仍能准确地预测出噪声水平值，将它们在BSD图像集合上进行测试，这些图像先被高斯噪声干扰然后再被添加了5%脉冲噪声.从表10的数据可以看出：高斯噪声在伴有脉冲条件下，MNLE算法都表现出了良好的稳定性.而其他参与对比的评估算法的评价准确性比较差，甚至完全失效，无法完成对高斯噪声水平值的估计.其实，高于5%脉冲噪声情况下，各个对比算法的预测效果更差，故不再给出更多的数据.这些情况说明脉冲噪声与高斯噪声对图像的干扰方式上是不同的，只要加入少许的脉冲噪声就可以对现有SNLE算法的估计结果产生严重影响，而MNLE的算法则不会受太多影响.虽然脉冲噪声影响了图像的统计特征值，但是影响的方式和规律是相同的.由于在样本库中存在着类似的样本，MNLE算法仍然可以实现准确的高斯噪声水平值估计.当然，基于MNLE算法的工作原理，也可以实现对脉冲噪声的比例值准确的估计，这不在本文的讨论范围内，故这里不列出相关实验数据.

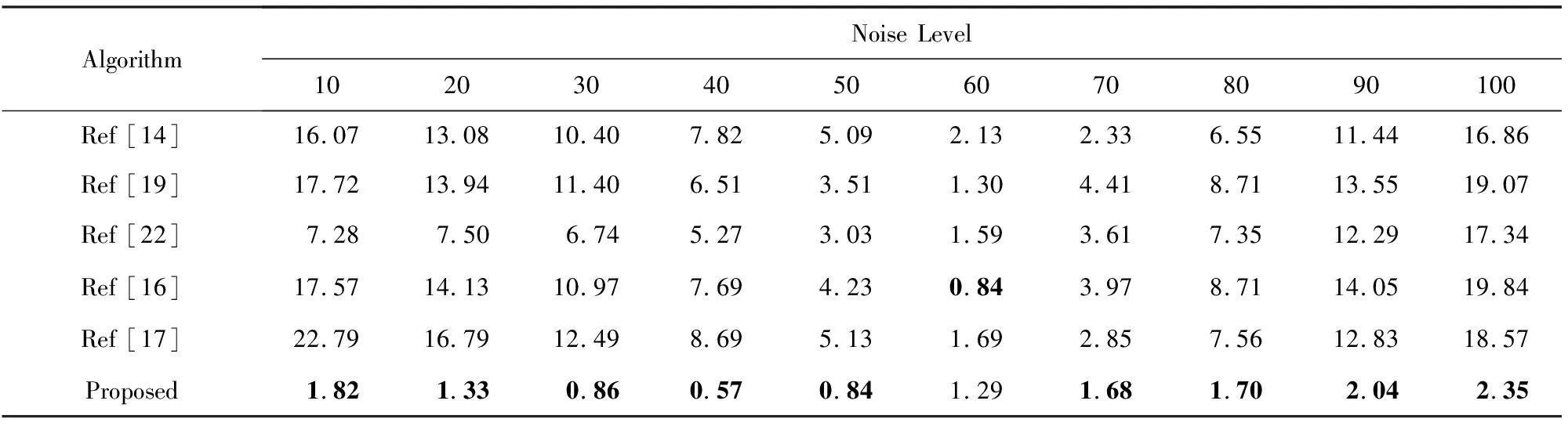
Table 10 RMSE Results on the Images from BSD Database Under Mixed Gaussian-Impulse Noise表10 高斯脉冲混合噪声下各算法在BSD图像集合上的均方根误差

3.4.2 伴有泊松噪声

实际应用当中，高斯噪声可能与泊松噪声混合在一起出现.由文献[28]可知，高斯泊松混合噪声是一种被称为信号相关噪声(signal dependent noise, SDN).SDN噪声模型的定义为

g(i,j)=I(i,j)+I(i,j)γ×μ+ω，

(11)

其中，g(i,j)是噪声图像像素值，I(i,j)是无噪声图像像素值，γ是控制着信号相关性的指数参数，μ和ω分别反映的是与信号相关和不相关的噪声参数.其中，当γ=0.5时，SDN模型就是高斯泊松混合噪声.为了验证MNLE算法的有效性，参照文献[28]，设置γ=0.5，σμ=0.5，而σω值的范围设定为0～100之间，它相当于纯高斯模型中的噪声水平值.表11中列出了各算法对伴有泊松噪声情况下高斯水平值的估计结果.可以看出：参与比较的各个算法则在中、高水平噪声条件下预测效果比较差，而MNLE算法继续保持了较好的稳定性.MNLE算法具有稳健的预测结果说明所提出的噪声水平感知特征仍然对高斯泊松混合噪声类型有效.另外，MNLE算法本质上属于基于样本的预测方法保证了预测准确率.只要在样本库中存在类似的失真图像，就可以实现准确的估计.

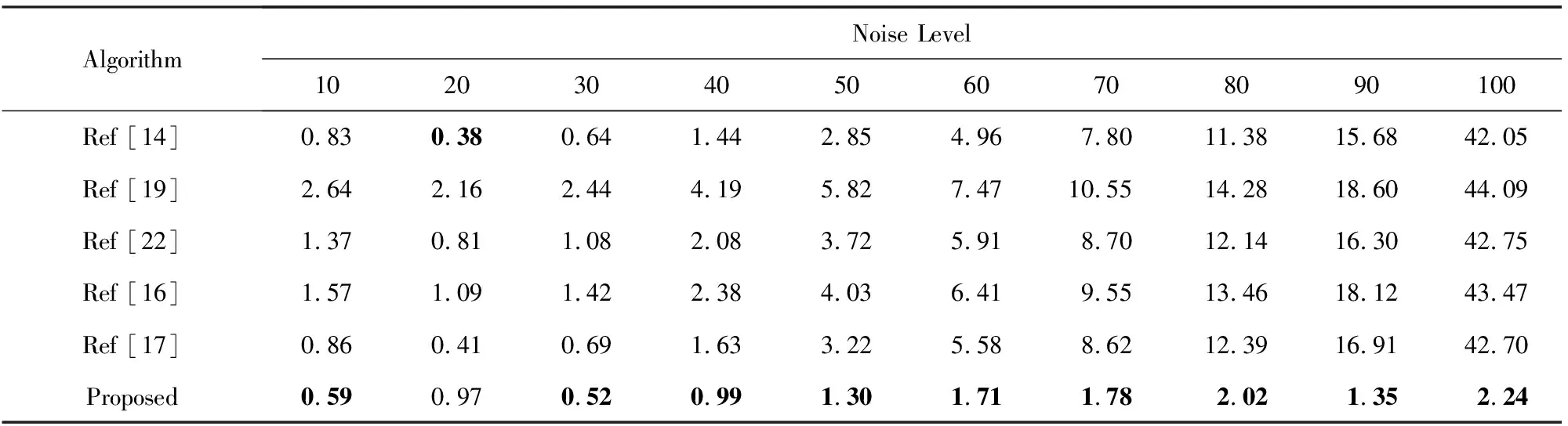
Table 11 RMSE Results on the Images from BSD Database Under Mixed Gaussian-Poisson Noise表11 高斯泊松混合噪声下各算法在BSD图像集合上的均方根误差

4 总 结

一直以来，基于噪声图像本身进行噪声水平估计的SNLE算法被认为是适应实际应用需求的实现策略，受到众多研究者重点关注.然而，现有SNLE算法普遍存在抗干扰能力低和执行效率不高的问题急需解决.在噪声水平感知特征提取技术的支撑下，本文提出了一种完全与传统方法不同的基于多幅样本图像的噪声水平评估MNLE算法.它核心的思想就是用噪声水平感知特征矢量刻画描述图像噪声水平值的高低，并从大量已知噪声水平的噪声图像上提取它们的特征矢量和对应的噪声水平值一起构成样本库.有了样本库先验知识，待评价图像的噪声水平值可以用在样本库中与待评价图像在特征矢量方面近似的若干样本图像所对应的噪声水平值的加权均值估计.大量的实验表明：MNLE算法不但预测准确性高、抗干扰能力好，而且执行效率还非常高，有效解决了SNLE算法存在的问题，非常适合作为各类降噪算法的前置模块来使用.