我国政府卫生支出的最优规模估算——基于面板数据模型的计量分析

傅书勇，孙淑军

(1.沈阳药科大学工商管理学院，辽宁 沈阳 110016；2.辽宁科技学院马克思学院，辽宁 本溪 117004)

改革开放以来，随着国家经济的快速发展，我国政府越来越重视卫生领域的投入。如1997年我国政府颁布的《中共中央、国务院关于卫生改革与发展的决定》中提到，“中央和地方政府对卫生事业的投入，要随着经济的发展逐年增加，增加幅度不低于财政支出的增长幅度……。”当前，我国政府面临经济速度放缓的态势，政府财政收入增速也呈现下降趋势，此时各级政府应合理确定政府卫生支出规模，实现既能保证人民必要的卫生支出，又能有效促进经济增长的一种动态平衡。

近年来，经济学家和学者也逐渐开始研究政府卫生支出最优规模，其逻辑关系为：若实际政府卫生支出高于最优规模，则会影响其他领域内的政府支出，也不利于长期的经济增长；若实际政府卫生支出低于最优规模，则会增加人民医疗负担和降低人民健康水平，进而会降低经济增长速度[1]。

国外学者研究政府卫生支出规模的文献较少，如Newhouse曾通过对发展中国家实证研究，认为GDP可以解释政府卫生支出的绝大部分[2]。国内也有少数学者对此问题进行研究，如王俊较早研究政府卫生支出规模，但未给出政府最优支出规模大小[3]。还有一些学者在研究我国政府卫生支出最优规模问题时产生较大的分歧，如李梦娜构建非线性计量模型，计算出1978-2002年我国政府卫生支出最优规模应占GDP的1.07%[4]；肖海翔等利用Barro理论与Karras计量方法进行实证分析，得出我国政府卫生支出最优规模应占GDP的11.9%[5]；王萱利用C-D函数和加入政府支出规模的教育人力资本生产函数等形式计算出政府卫生支出的最优规模为4.74%[6]。

事实上，上述研究可能存在一定的问题，如或者未对时间序列数据进行平稳性检验，或者建立计量模型时缺乏一定的理论基础，或者模型中推导出现一定错误，或者未对模型进行多重共线性检验等，因此研究结果存在较大差异。

在应用多元回归分析建立的计量经济模型时，如果所建的模型中缺失了某些不可观测的重要解释变量，使得回归模型随机误差项常常存在自相关，此时回归参数的最小二乘法OLS估计量不再是无偏估计或有效估计。但是，运用面板数据建立的计量经济模型时，对于一些忽略的解释变量可以不需要其实际观察值，而通过控制该变量对被解释变量的影响的方法获得模型参数的无偏估计。由此可见，面板数据不仅可以同时利用截面数据和时间序列数据建立计量经济模型，而且能更好地识别和度量单纯的时间序列模型和单纯截面数据模型所不能发现的影响因素，它能够构造和检验更复杂的行为模型[7]。

因此，本文利用面板数据模型建立我国经济增长和政府卫生支出之间的协整回归模型，并进行平稳性检验(单位根检验)、Johansen协整检验、面板数据模型判别等检验方法，最后得到我国政府卫生支出最优规模的计量结果。根据政府卫生支出与经济增长之间的正向或负向关系，提出东部、中部、西部三大地区政府增加、保持还是降低政府卫生支出建议，从而为实现各地区政府经济增长与政府卫生支出之间相互促进发展提供参考。

1 数据、变量和模型

1.1 计量模型

假设国民经济生产函数为：Y=F(K，L，G)，Y是真实产出水平、K是资本存量、L是劳动力、G是政府卫生支出规模。同时认为该生产函数是规模报酬不变的，即对于变量乘以非负常数C可以使得产量同比例增加，得到cY=F(cK，cL，cG)，令c=1/L，则生产函数可写成：Y/L=F(K/L，1，G/L)，即为y=f(k，g)，k=KL和g=GL，分别表示人均资本存量和人均政府卫生支出。将该函数求全微分，可得y·=f·k·+f·g·，

两边同时除以y，可得y·y=f·k·y+f·g·y，亦可写成，y·y=εkk·k+εgg·g①，其中，εk=∂y∂k×ky，εg=∂y∂g×gy，分别表示K和g产出弹性，g的产出弹性也可以写成边际产出的形式，εg=MPg×gy②，由此可知，若是能求得人均政府卫生支出的产出弹性，即可求得其边际产出的大小。根据Barro法则，当政府卫生支出边际产出为1时，此时政府卫生支出最优规模等于其弹性。

1.2 数据来源及说明

本文政府卫生支出、固定资本形成总额、支出法GDP、从业人员原始数据来自2005-2016年《中国统计年鉴》及各省市2005-2016年统计年鉴，并经整理得到。由于《中国统计年鉴》中各省市的政府卫生支出数据最早公布在2004年，因此，数据最早截止到此年份。采用永续盘存法估算资本存量[8]，人均GDP、人均资本存量、人均政府卫生支出分别记为y、k、g，并将政府卫生支出、GDP、资本存量数据以GDP平减指数进行处理，三变量增长率y^、k^、g^，具体数据见表1所示。

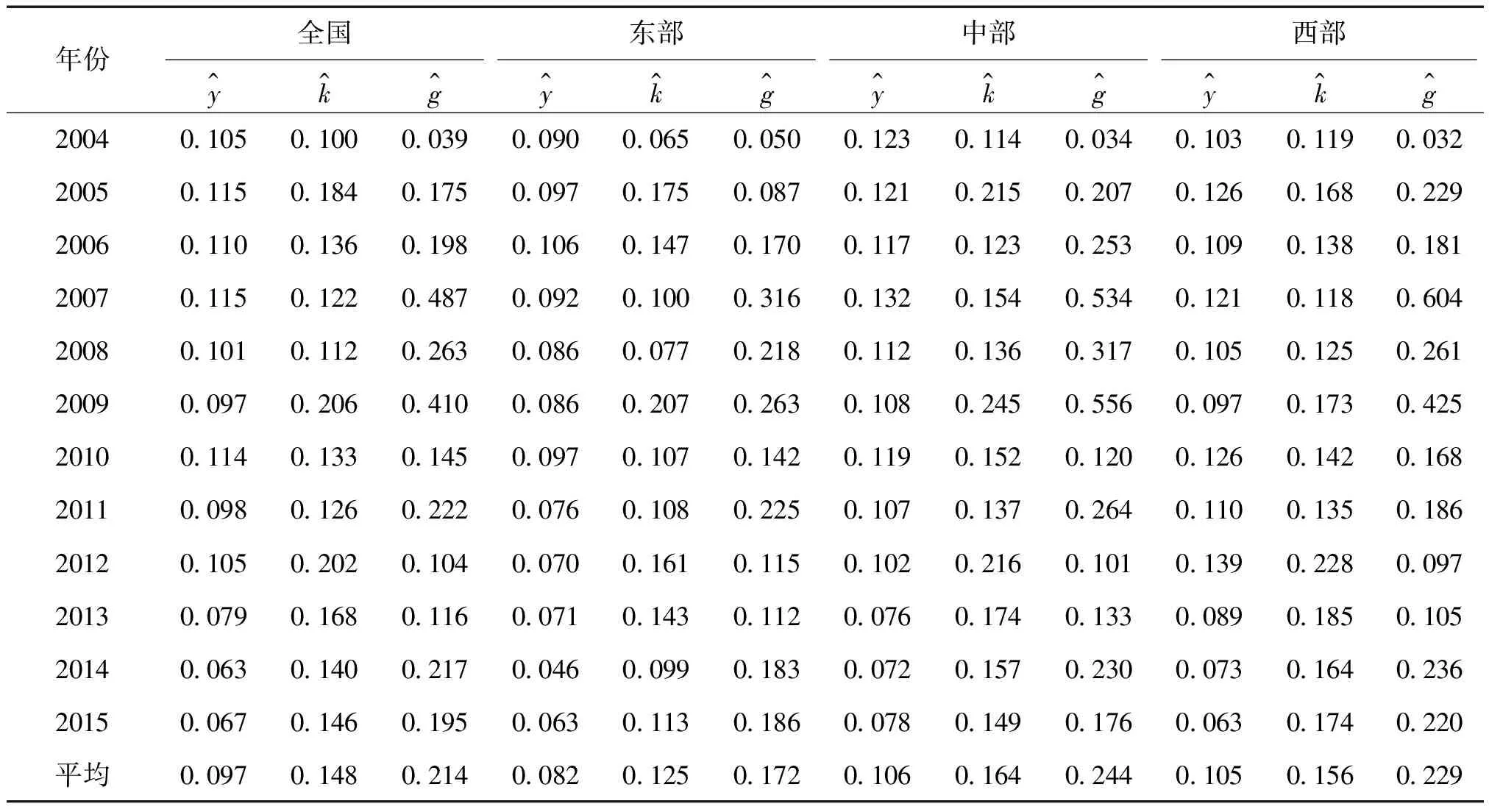
表1 基本数据描述性统计

2 面板数据模型

面板数据能更好地识别和度量时间序列或截面数据未能估计的效应，并有助于建立和检验更复杂的模型，其基本模型是如下形式的一般回归模型：

yit=α+xitβit+δi+γt+εit(i=1,2,…,N；t=1,2,…,T)

其中，yit是个体i在时间t时期的观测值，α表示模型的常数项，δi代表固定或者随机的截面效应，γt代表固定或者随机的时期效应，xit表示k阶解释变量观测值向量，β表示解释变量的系数向量，以模型(1)为基础，解释变量为人均资本增长率k^和人均政府卫生支出增长率g^，被解释变量为人均GDP增长率y^。

我国省份较多，各省份之间由于经济发展水平不同，可能存在一定的差异，因此，本文以全国、东部、中部和西部省份建立4个面板数据模型。东部地区包括：北京、天津、河北、上海、江苏、浙江、福建、山东、广东、海南等10个省、自治区、直辖市；中部地区包括：山西、内蒙古、安徽、江西、河南、湖北、湖南等7个省、自治区；西部地区包括：重庆、四川、贵州、云南、西藏、陕西、甘肃、宁夏、青海、新疆10个省、自治区、直辖市。由于东北三省数据未能通过平稳性检验，因此，暂不做面板数据研究。

2.1 单位根检验

由于多数时间序列数据都呈现明显的非稳定单位根过程的特征，因此若不对经济变量进行平稳性检验，而直接建模则易于产生伪回归现象。面板数据包括了时间维度和截面维度的数据，时间维度较小时，可以用面板数据直接建模，但时间维度增加到一定长度时，则需要对面板数据进行平稳性检验，即单位根检验。本文时间维度为12年，时间较长，因此，需要采用单位根检验数据的平稳性。

面板数据的单位根分为两类，一类是相同根情形下的单位根检验，ρi=ρ；另一类为不同根情形下的单位根检验，即允许ρi跨截面变化。本文采用两种单位根检验方法进行检验，相同根情形下的单位根检验采用LLC检验，不同单位根情形下采用ADF-Fisher检验方法，检验结果如表2所示。

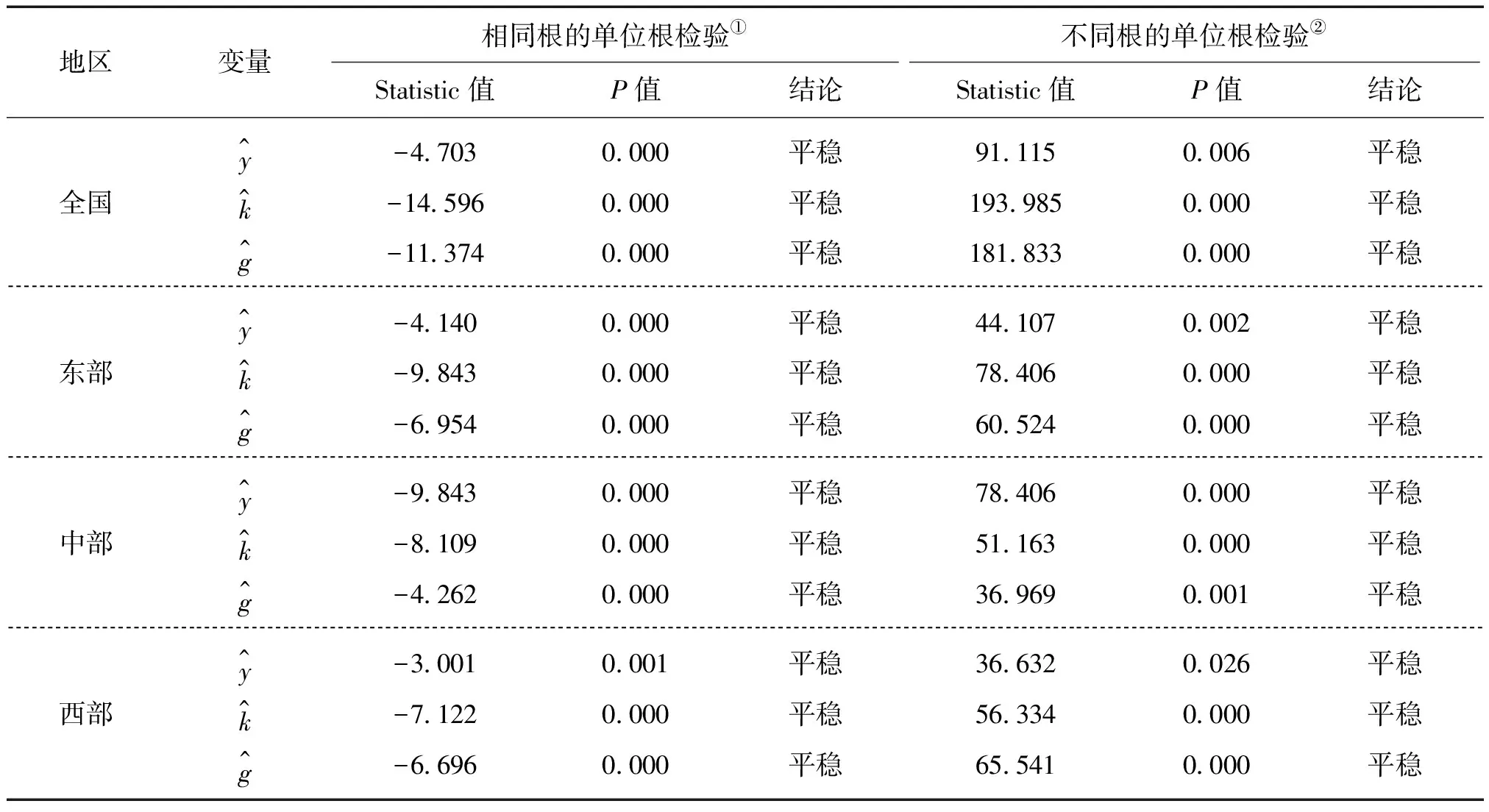
表2 单位根的检验

注：单位根的检验形式(C，T，K)为(C，T，I)。①采用的检验方法是Levin，Lin&Chu t；②采用的检验方法是ADF-Fisher Chi-Square。

由表2可知，在相同根和不同根的两种假设下各地区数据均通过平稳性显著性检验，可知各模型中的数据是平稳的。

2.2 协整关系检验

经济变量之间存在的长期均衡(静态)关系被称为协整关系。从经济意义上看，这种协整关系的存在表现为系统内某一变量的变化会影响其它变量的变化，一次冲击只能使协整系统短时间内偏离均衡位置，在长期中它会自动恢复到均衡位置。目前共有3种基于面板数据的协整检验方法，分别为：Pedroni检验、Kao检验和Fisher检验。Pedroni和Kao协整检验是从Engle-Granger两步(残差)协整检验发展而来的；而Fisher检验则是合并了的Johansen检验。与Kao检验方法不同的是，Pedroni检验方法允许异质面板的存在，Pedron在零假设是在动态多元面板回归中没有协整关系的条件下给出了7种基于残差的面板协整检验方法[9]，综上所述，本文采用Pedroni检验方法，具体数据如表3所示。

表3 协整关系检验

注：①采用的检验方法是Panel ADF-Statistic；②采用的检验方法是Group ADF-Statistic。

由表3可知，相同单位根条件下，全国模型及其加权后的ADF协整检验值分别为2.808、2.597，其P值分别为0.998、0.995，均远远大于0.05。因此，应接受原假设，即存在协整关系。同理，东部、中部和西部地区均通过协整关系检验，可以接受原假设，即存在协整关系。不相同单位根条件下，全国模型ADF协整检验值为4.102，其P值为1.000，远远大于0.05，因此，应接受原假设，即存在协整关系。同理，东部、中部和西部地区均通过协整关系检验，可以接受原假设，即存在协整关系。

2.3 面板数据模型类型判别

在进行面板数据模型实证分析时，需要确定采用固定效应还是随机效应。Hausman提出一种检验这个假设的方法，即首先采用随机效应模型进行实证，然后采用进行Hausman检验，除非统计值拒绝原假设，否则应使用随机效应模型[10]，以上各模型的检验结果如表4所示。

表4 面板模型类型判别Hausman检验情况

由表4可知，全国、东部和西部地区面板数据模型的Hausman检验的P值均小于0.05，因此拒绝原假设，可以推断3个模型比较适合固定效应模型；而中部地区面板数据模型的Hausman检验的P值大于0.05，因此接受原假设，即适合采用随机效应模型。

2.4 面板数据实证结果

经过上述面板数据模型相关检验后，可以对4种模型进行面板数据模型分析，计量结果如表5所示。

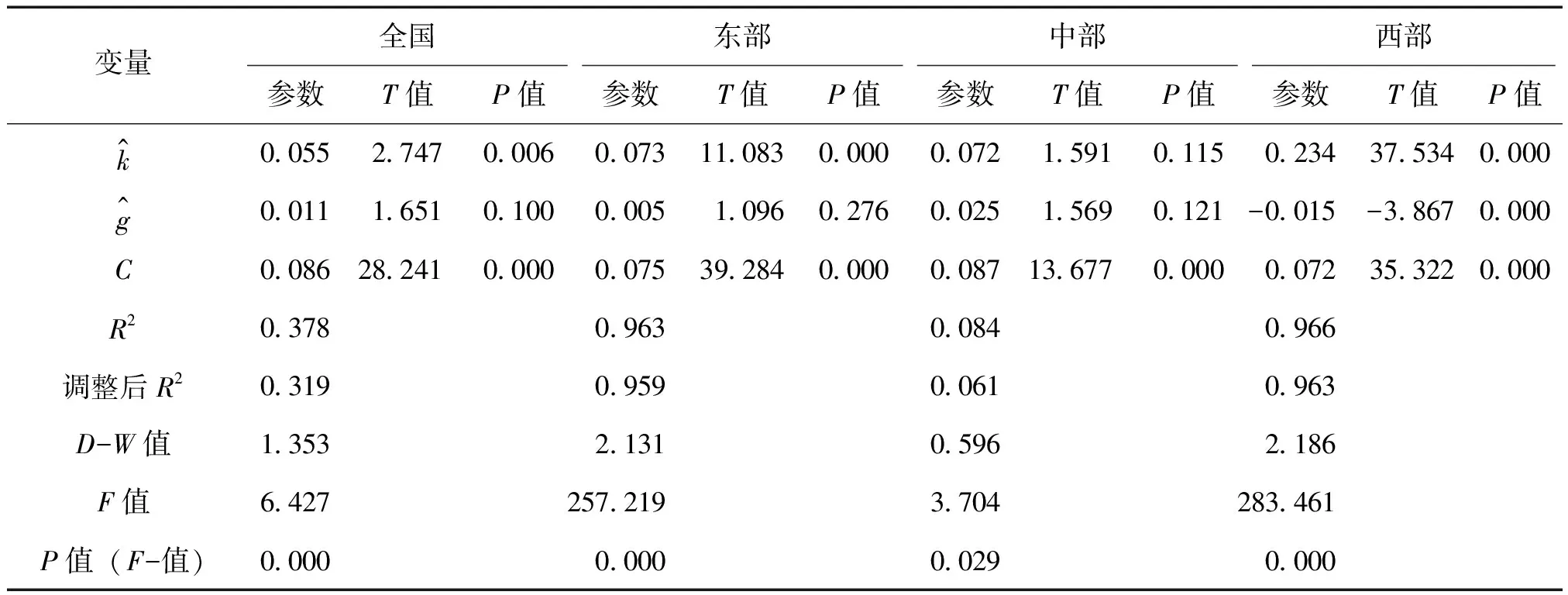
表5 各模型的计量结果

由表5可知，除中部地区拟优度为0.084较低外，东部和西部地区拟优度分别为0.963、0.966，均为0.9以上，说明东部和西部模型拟合效果较好。由于山西省近几年来的经济转型问题，暂将山西省移除中部地区，可得模型Hausman检验的P值为0.530，仍采用随机效应模型，此时拟优度为0.134，政府卫生支出的弹性系数0.025，资本存量的弹性系数为0.089。全国、东部地区政府卫生支出的弹性系数均为正值，分别为0.11、0.005，且通过了10%、30%显著性水平检验，这3个地区提高人均政府卫生支出增长率，能够促进这些地区的经济增长；西部地区为负值，为-0.015，且通过了1%的显著性水平检验，说明西部地区人均政府卫生支出增长率对经济增长产生了负效应。全国、东部、中部和西部地区资本存量的弹性系数均为正值，分别为0.055、0.073、0.089、0.234，说明这些地区增加资本存量仍会促进经济增长。

3 讨论与建议

3.1 较发达地区政府卫生支出可能会促进经济增长

由表5可知，虽然东部和中部地区的人均政府卫生支出弹性系数通过检验的显著性水平较高一些，P值分别达到0.276、0.121，但从某种意义上来说，这些地区的人均政府卫生支出对经济增长存在正效应。由表1可知，虽然东部地区经济增长率和政府卫生支出增长率均低于中西部地区，但其前期的资本积累已经达到较高规模，基础设施也基本较为完善，特别是城市居住环境好于中西部地区，在此基础上，政府卫生支出对经济增长呈现正效应，建议这些地区应保持政府卫生支出与经济增长同比例增长，且优化政府卫生支出结构[11]。

中部地区经济增长率、资本存量增长率和政府卫生支出增长率均高于东部和西部地区，原因在于这些地区承接东部地区的产业转型，获得较多的资本投资，且由于政府逐渐增加了财政收入，所以政府提高了相应的政府卫生支出规模，从而形成资本投资促进经济增长，经济增长增加政府财政收入，政府财政收入增加提高政府卫生支出规模，进而促进本地区健康人力资本的增加，最终又推动经济增长的良性循环。因此，建议这些地区在优化政府财政支出，逐步完善基础设施建设，建立良好的生活环境的同时，保持略高于经济增长的政府卫生支出增长率，长远来看，更能促进经济持续增长[12]。

3.2 欠发达地区政府卫生支出可能对经济增长产生负面效应

由表5可知，西部地区人均政府卫生支出弹性系数为负值，对经济增长呈现负效应，又据表1可知，西部地区经济增长速度高于东部地区，略低于中部地区，但资本存量增长率和政府卫生支出增长率均低于中部地区。由此可推断，与中部地区相比，西部地区缺乏区位优势，即在承接东部地区产业转移过程中，处于劣势地位，资本存量增长率较低。因此，建议这些地区保持低于经济增长率的政府卫生支出增长率，加大资本投资力度，将更多的政府财政支出用于政府投资或购买，引起一定的乘数效应，促进本地区的经济增长，经济增长会增加政府财政收入，未来再增加政府卫生支出规模[13]。

综上所述，全国、东部、中部和西部地区政府卫生支出的最优规模为0.011、0.005、0.025和-0.015，与其他学者研究结果相比较低一些，其原因或许与政府卫生支出结构、卫生体系差异等因素有一定关系，由于篇幅有限和研究目标不同，这些内容作为未来的研究方向之一。