电能质量综合评估研究

张明浩，何娟，李堃

（贵州大学，贵州 贵阳550025）

0 引言

随着社会的发展，传统的电能质量评估方法已经不能满足人们对电能质量的要求。尤其是近十几年来基于计算机，电力电子等敏感设备在负荷中的比重越来大。由暂态电能质量问题导致的设备故障日趋增多，在部分地区由电压暂降引起的客户投诉占电能质量投诉的80%以上，并造成巨额经济损失[1]。因此把暂态电能质量指标纳入电能质量指标体系显得尤为重要。

国内外一些专家已经提出一些电能质量指标评估的方法。文献[1]采用基于加权法评估电能质量指标。文献[2]提出了一种考虑供电系统与敏感负荷的电压暂降严重程度评估，利用法确定系统侧和负荷侧特征指标权重，法确定的权重比较主观，没有充分考虑电压暂降与敏感设备耐受度的不确定性。文献[3]提出用模糊神经网络法来评估电能质量，但是对于电压暂降的特征量，文章只考虑了暂降幅值的影响，并没有将暂降持续时间纳入考虑范围。文献[4]提出采用法和主客观权重相结合的方法来综合评估电能质量，但是文中只考虑了稳态电能质量，并没有考虑暂态电能质量的影响。

本文从稳态电能质量指标和暂态电能质量指标两个方面考察节点的电能质量情况。暂态电能质量指标通过电压暂降事件对敏感设备的影响度来判定，首先建立引起电压暂降关键致因的随机概率模型，通过蒙特卡洛模拟得到电压暂降关键特征量的期望及概率密度函数，结合电压暂降关键特征量和敏感设备的耐受度计算暂态电能质量指标。以国家标准规定的电压偏差，电压波动，三项不平衡，谐波含量，频率偏差作为稳态电能质量问题的特征量，稳态电能质量采用法与客观权重计算相结合的方法，克服法主观性过强的缺点。最后通过敏感设备在负荷中所占的比重计算出稳态电能质量指标和暂态电能质量指标的权重，得出电能质量评估综合指标。

1 基于蒙特卡洛法的暂态电能指标的计算

本文采用蒙特卡洛模拟出某一节点的电压暂降幅值与持续时间的期望值，然后结合敏感设备的电压耐受曲线计算出敏感设备的停运概率，进而计算出遭遇暂降时间后设备正常运行的概率，作为评价暂态电能质量的指标值。

1.1 建立故障概率模型

本文主要研究短路故障引起的电压暂降，考虑以下4个关键致因因素，分别为故障类型、故障线路、故障位置、继电保护装置动作时间[6]建立随机概率模型。节点的电压暂降特征量可以描述为：

式中：Usag表示电压暂降幅值；Tsag表示暂降的持续时间；F1F2F3F4分别表示故障类型、故障线路、故障位置、继装置动作时间的随机概率模型。

（1）故障类型的概率密度函数。本文主要考虑4种故障类型即单相接地短路、相间短路、两相接地短路、三相短路。故障类型的概率密度函数可以用随机数X1的分布来表示。

式中为服从均匀分布的随机数，X1～U(0,1)。1～4分别代表4种故障类型。P1为单相接地故障的统计概率，P2为相间短路故障的统计概率，P3为两相接地短路的统计概率，P4为三相短路的统计概率。

表1 P1，P2，P3，P4的统计概率表Table 1 Statistical probability table of P1，P2，P3，P4

（2）故障线路的概率密度函数。导致线路故障的因素多随机性大难以用数学模型精确描述，因此我们将故障线路发生的概率简化，线路长度越长其发生故障的概率越大[5]。某一线路发生故障的概率可以描述为：

式中n代表系统中线路的条数，li代表第i条线路的长度，Pil代表故障发生在第li条线路上的概率。线路故障的概率密度函数可以用随机数X2的分布来表示

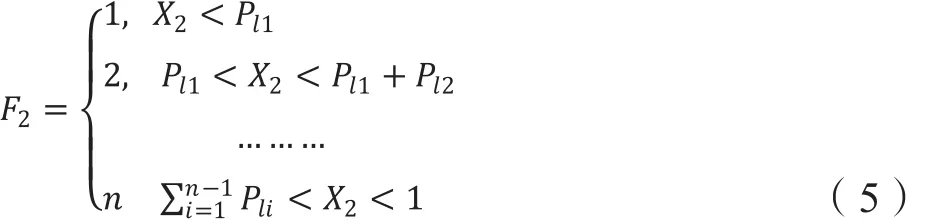
在上式中，X2表示服从均匀分布的随机数，X2～U(0,1)。1～n表示那一段线路发生故障。

（3）故障位置的概率密度模型。设同一条线路上每个位置发生故障的概率均等，则可以用X3～U(0,1)来模拟故障发生的位置。

（4）故障持续时间的概率密度模型。故障持续时间取决于线路中的短路器，负荷开关等电气设备的动作时间。但由于电气设备本身的性质可能无法在标准时间内动作，其动作保护时间满足以下概率分布模型[7]：

其中为开关设备动作的平均时间，令T0=60 ms，K为概率分布值的拟合系数，令K=0.2，X4表示服从均匀分布的随机数，X4～U(0,1)电压暂降特征量的期望值仿真计算。

要保证模拟仿真结果的误差ε小于0.03，至少需要进行4445次仿真计算[6]。为了进一步减小误差提高可信度，本文进行5000次仿真计算。

由于进行模特卡罗模拟的抽样仿真次数过于庞大，为了加快仿真速度，可以列举所有故障特征量和与其对应的暂降特征量并保存为数据库，选取随机变量后直接从数据库中调取数据即可。其仿真流程图如下所示：

图1 模特卡洛模拟流程图Fig. 1 Flow chart of Monte Carlo method

1.2 结合设备耐受度曲线计算暂态电能质量指标

在IEEE Std.1346-1998中列出了6种不同设备类型的耐受曲线。这6种耐受曲线都呈矩形，其不确定域可由图一所示，图中Umax和Umin为敏感设备耐受曲线的电压上下限，Tmax和Tmin为敏感设备耐受曲线的暂降持续时间上下限。当暂降事件落在曲线1的上方时，设备不会受到影响当暂降事件落于曲线1和曲线2之间时设备有可能发生故障，当暂降事件落于曲线2下方时设备必定发生故障。暂降事件越接近曲线2设备故障概率越大，因此可视作与满足累计分布[7]。

图2 设备耐受度曲线Fig. 2 Uncertainty region of equipment VTC

我们可以认为当暂降事件落于B区域时，设备发生故障的概率只和U有关，越靠近Umin故障发生故障的概率越大。当暂降事件落于C区域时同理，设备发生故障的概率只和T有关，越靠近Tmin设备发生故障的概率越大。当暂降事件落于A区域时，设备是否故障可以由能量损失的大小来判断，用能量损失公式构建累计分布概率函数来计算设备停运率[8]。由于我们在构建节点暂降特征量时暂降的幅值和暂降持续时间是相互独立的，因此可认为T与U是相互独立的变量。因此设备停运概率可表示为：

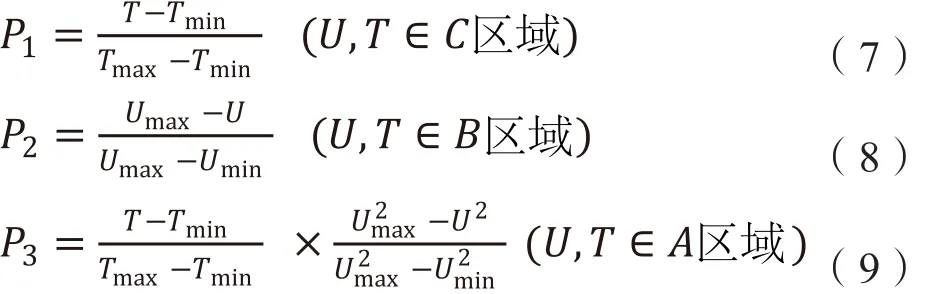
其中和为蒙特卡洛模拟计算出的期望值。

因此第个节点的暂态电能质量指标为：

2 基于层次分析法的稳态电能质量指标计算

2.1 AHP法的层次结构

本文将电能质量指标分为3个层级，1级指标层包括电能质量稳态指标，2级指标层包括电压类指标、频率类指标和可靠性指标，3级指标层包括国家规定的各项电能指标，电压波动、电力谐波、电压偏差、三相不平衡、频率偏差和供电可靠性。电能质量稳态指标的层次结构如下所示[9-10]：

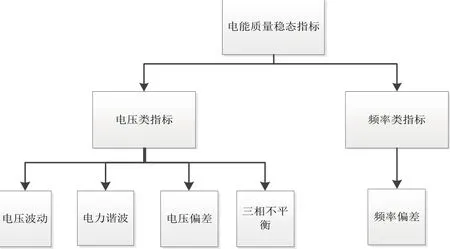
图3 电能质量稳态指标的层次结构Fig 3. Hierarchical structure of steady state indicators of power quality

2.2 稳态电能质量指标的优属度函数

以电能质量特征指标的满足程度，构造其相对优属度。相对优属度指相对“优”的程度，它借助模糊数学的概念用类似于隶属度的含义来描述。电能质量特征指标可以分为固定型、区间型、成本型 3 种目标类型[11-12]。

①固定型是指一个特征指标稳定在某一个固定值时为最优，当特征指标偏离这个固定值时，它“优”的程度逐渐下降[13]。比如频率偏差就是一个的固定型特征指标，当频率偏差为0时达到最优。当频率出现偏差时“优”的程度下降。固定型特征指标的数学表达可以描述为：

其中fi为特征指标的第i个观测值，f*为特征指标的最佳值，为fi与f*之差的最大绝对值。

②区间型指标是指属性值以落在某个固定区间内为最佳的一类特征指标[14]。其相对优属度的数学表达可以描述为：

③ 成本型特征指标指属性值越小越好的指标。其相对优属度描述为：

分析电能质量问题的特征指标可以得出特征指标类型。电能质量问题、电能质量特征指标和特征指标所属类型如下表所示[15]：

表2 电能质量问题、电能质量特征指标和特征指标所属类型Table 2 Power quality problems, power quality characteristics indicators and types of characteristic indicators

2.3 稳态电能质量指标的计算

对含有n个节点的m个电能质量指标进行评估，先根据各节点的测量值形成目标决策矩F，其中:

然后结合各电能质量指标的目标类型[16]，将目标决策矩阵转换为相对优属度矩阵：

根据图2的层次结构，引入三角模糊数形成模糊判别矩阵。判别矩阵建立的方法为，两两比较下层元素相对与上层元素的重要性。通常采用标度1-9和其倒数来表征其重要程度。其含义如下[17-18]：

表3 模糊判别矩阵的取值和含义Table 3 The value and meaning of fuzzy discriminant matrix

通过两两比较可以得出模糊比较判别矩阵：

在模糊比较判断矩阵中，指标相对于本层其它指标的模糊相对权重向量为:

为排序比较，需要将模糊相对权重向量清晰化。按照清晰化后的值作为电能质量稳态指标的权重值，清晰化方法如下[19-20]：

在评估过程中出现某单项指标不合格的情况，视为综合评估值为不合格。则第个节点的稳态电能质量指标如下:

3 电能质量指标的综合评估

通过以上分析，已经得到电能质量的暂态指标和稳态指标，然后通过敏感负荷在所有负荷中的占比来调整暂态指标和稳态指标的权重。

表4 各站点的电能质量数据和敏感负荷占比Table 4 Power quality data and sensitive load ratio

4 算例分析

4.1 稳态电能质量指标的计算

按照上述方法对某地区的电能质量进行综合评估，该地区电能质量数据和敏感负荷占比如表4所示。

首先计算稳态电能质量，根据表4建立目标决策矩阵F：

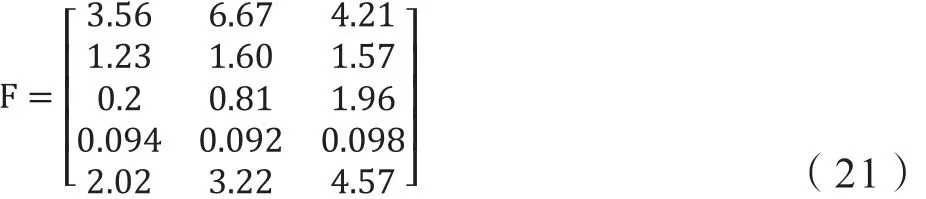
根据目标决策矩阵和相应的国家标准结合优属度函数建立优属度矩阵：

模糊判别矩阵采用文献中所提供的数据，根据模糊判别矩阵可以计算出每项电能质量指标的权重向量和相应的权重，如表5所示。

表5 电能质量问题的权重值Table 5 Weight value of power quality problem

由表5中的各个电能质量问题的权重值和优属度矩阵可以计算节点的稳态电能质量指标，Q21=0.6003、Q22=0.4160、Q23=0.3966。

4.2 暂态电能质量指标的计算

先根据当地电网建立仿真模型，然后通过蒙特卡洛模拟法计算出电压暂降事件的暂降幅值和暂降持续时间期望值。通过蒙特卡洛模拟法得出节点的电压暂降特征量的期望值:

表6 电压暂降特征量的期望值Table 6 Expected value of voltage sag characteristic

用PLC设备的耐受曲线参数作为敏感设备的参考。其中PLC设备耐受曲线的Umax=0.78，Umin=0.47，Tmax=0.6，Tmin=0.02。由此可知三个节点的电压暂降事件均落于不确定域的A区域，由能量损失公式构建累计分布函率函数来计算设备停运率，计算结果为节点1停运概率为0.710999,节点2停运概率为0.206079，节点3停运概率为0.514611。因此节点1、2、3的暂态电能质量指标分别为：Q11=0.289、Q12=0.7939、Q13=0.4854。

结合各个节点的稳态和暂态电能质量指标，求出节点电能质量综合评估指标：Q1=0.444644、Q2=0.453769、Q3=0.423251。

可以看出节点1的稳态电能质量指标较好，但是暂态电能质量指标较差，而且在节点1中敏感负荷的占比较高，因此最后的综合评估指标反而不如节点2。由此可见，在考虑评估电能质量综合指标时，仅从一方面衡量是远远不够的。尤其是对于有敏感负荷的工业园区，在评估其电能质量时，应该考虑到稳态电能质量问题和暂态电能质量问题，并且根据园区的实际情况调整权重，最后得出能真正反应出实际问题的指标值。

5 结论

本文通过蒙特卡洛模拟计算出各个节点电压暂降特征量的期望值，通过暂降期望值计算暂态电能质量评估指标，通过层次分析法计算稳态电能质量指标，其结果表明：

（1）由于电压暂降主要由故障导致，而故障通常是随机发生的。蒙特卡洛模拟仿真能较好的处理随机过程，在仿真模型精确，概率密度函数较为客观的条件下可以很好的模拟暂降事件的特征，得到的结果可信度高。

（2）采用基于能量损失的设备敏感度模型能更准确地反映设备停运的实质，进而更有效地分析评估暂降事件对于用户的影响程度。

（3）在评估过程中考虑稳态指标和暂态指标，评估结果对该节点的敏感用电设备和非敏感用电设备都有指导意义。