基于风能转换系统的多层次多模型预测控制

王俊，秦斌，祝兴星

（湖南工业大学电气工程学院，湖南 株洲 412008）

0 引言

风能因为其具有大规模开发和商业化发展前景等原因，已经成为可再生能源中发展最迅猛的清洁能源。在厄尔尼诺现象越来越明显的背景下，全球的风能迅速发展，预计到2020年前后，风电将成为火电、水电之后的常规发电电源。积极发展可再生能源，对于增添能源供应，调整能源结构，保障能源安全都具有重要作用[1]。

风能转换系统有太多的不确定属性即非线性，其控制过程比较复杂。虽然风能转换系统的不确定属性研究已经取得了很多研究成果，但是由于取得高精度非线性系统模型艰难、非线性微分方程逼近等一系列问题，非线性控制器的发展存在着许多缺陷[2]。针对这些问题，在分解数据合成模型的策略基础上提出的多模型方法[3]成为非线性系统建模的重要方式。多模型方法的基本操作是首先将整个区间划分成若干个子区间，每个子区间当成一个层次的，然后在每个层次区间上建立对应的子模型，最后根据阶成规则获得当下时刻系统使用的实时模型。

多模型方法和预测控制方法的联合是解决非线性系统控制问题的重要方法之一。多模型预测控制算法的研究主要包括：非线性系统子区间的分袂、多模型的建模、模型的切换方法等.非线性系统子区间的划分主要可以通过数据聚类分析来划分。多模型模型建模方法的研究，主要有最偏最小二乘法建模[4]、混合逻辑动态模型[5]等。当前多模型的切换方法主要有软切换和硬切换两种方法。软切换注重权重系数的选择本文选择选用输出误差指标[6]来确定权重系数。硬切换的关键是切换指标的选择，本文选用反馈误差指标[7]来决定切换指标。

当非线性系统工况发生变化时，传统的控制效果很难达到期望的目标。工况发生变化时的多变量系统的控制问题多而杂，很多现有的解决方案[8]仍然有必要进一步研究。为此，在风能转换系统基础上，把多层次多模型与预测控制相结合，运用此方法对风能转换系统过程进行控制。仿真结果表明，在遇到扰动时该切换方法仍然能够使得系统具有较的好动态特性和抗干扰性。

1 风能转换系统的模型与控制方法

风能转换系统（图1）的风速为Vt，桨距角设定值为βref(t)和电磁转矩设定值Tgref(t)，系统的输出为发电机功率Pg(t)和高速轴转速ωg(t)

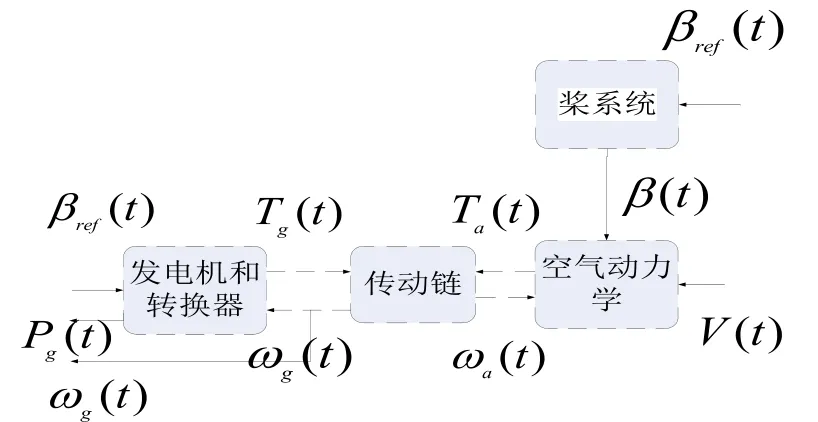
图1 风能转换系统的结构图Fig.1 Wind energy conversion system structure diagram

1.1 风模型

风由低频率风速跟高频率风速叠加而成[9]，由公式（1）知，Vm(t)是平均风速，其频率比较低；Vs(t)是快湍流部分风速，其频率比较高。

1.2 空气动力学模型

当有风穿过风轮旋转而形成的平面面积时风的输出功率表示为：

公式中：A为风叶旋转而形成的表面面积，Pw为风的输出功率，V为受力风速,ρ为在一定的温度和压力下单位体积空气所具有的质量。由风的有效功率Cp(λ，β)知，功率系数的大小随着风轮旋转速度和来流风速V、桨距角β变化而变化。风轮有功功率：

公式中：Pa为转子有功功率。

叶尖速比定义为风轮旋转而形成的平面面积与来流风速的比值：

式中：ωr是低速轴转速。

1.3 传动链模型

传动链是传递风能的主要装置，由低速轴、高速轴、齿轮以及弹性装置组成。传动链动态方程如下：

式中：Jr为低速轴转动惯量Jg为高速轴转动惯量，Ks是传动链的弹性装置的劲度系数，DS为传动链的弹性装置的阻尼系数，Ng为齿轮比，δ为柔性传动链的扭转度，并且δ·=ωr-(ωg/ Ng)。

1.4 桨距系统模型

用一个二阶模型来表示[10]变桨距控制系统，其状态方程为：

1.5 发电机和变流器模型

发电机与整流器模型用一阶模型表示。电磁子系统：

式中：τg为时间常数。时发功率可描述为：

由上述可以知道的各个部分的模型，我们可以得到整个风电机组的完整模型：

1.6 控制方法

风电机组的控制方式如图2所示。

图2 风机电组的控制策略Fig.2 Control strategy of wing turbine

风电系统在不同的风速时对功率和转速均有不同的控制要求。一般来说在风速的大小没有到达能使风能机指定的要求时，风机是不会运行启动的；在风速的大小到达能使风能机启动的指定要求时但未达到风能机额定的风速大小时，风机的风能效率得控制到最大；当风速超过额定风速的大小则需要抑制风能功率继续上升来避免风机过负荷，同时保持系统稳定。

风速在[0 4]m/s时不能是风机开始运行，系统处于待机状态。风速在[4 16]m/s时系统处于负荷状态控制的主要目标在于捕获最大的风机功率。通过控制β和Cp（λ，β）取得最适值，当风速超过额定时，应注意控制高速轴转速ωg的值不要超过电机的阈值转速。

当风速超过额定16m/s时段又称过负荷段，此时首要任务是控制风能机使发电机功率Pg保持在发电机的额定功率值Pgnom。同时限制高速轴转速 ωg维持在 [ωgnomωgmax]之间。

在最大风速高于切出风速，改变桨距角的值以尽量减少风速与扇叶的有效面积。同时系统与电网断开，电机停止运行。

2 多层次多结构模型与预测控制算法步骤

多层次多结构模型是将整个工作区间划分为不同的子空间，这些子空间作为不同的层次。然后把每个不同的层次空间划分为更为详细的子空间，最后构造相应的模型。系统中的子模型包括多个层次的多模型，如图1所示，其中，Li代表第i层次，Li,j代表第i层的第j个子模型。

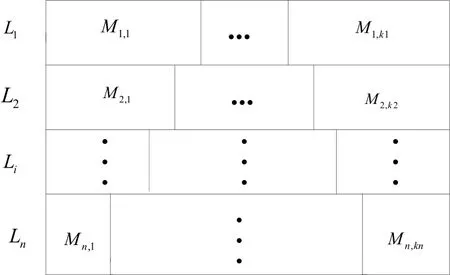
图3 多层次多模型结构图Fig.3 The structure Multi-level multi-model

通过分析风能转换系统特性和工况变化把传动链桨叶控制分为两个部分，从而建立层次结构模型集;针对每一个部分，根据风机运行时云数据的特征采用参数辨识方法分析建立相对应系统的固有振动特性，从而获取非线性系统的层次结构模型；然后依据固有的振动动态特性，设计一个最实用的模型调度方法，通过在调控规则内对不同层次不同子模型之间进行切换;最后依据此时此刻的动态预测模型来设计符合系统要求的预测控制器，来落实对真实系统的控制[11]。其工作原理如图4所示。

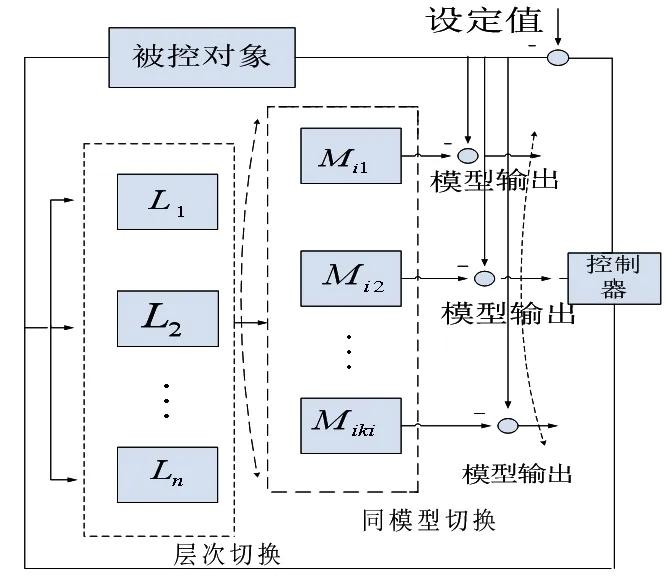
图4 多层次多模型预测控制算法原理结构Fig.4 The principle of Multi-level multi-model prodictive control

多层次多模型预测控制算法步骤如下:

（1）把系统划分不同的层次，在不同层次输出通道上再建立层次的子模型，最后根据实时数据获得每个子模型参数；

（2）根据实际工况，选择合适的切换方法并且判断当前时刻不同层次最适用的子模型；

（3）针对最适用的子模型集，选用多变量广义预测控制(Generalized predictive control, GPC)算法[12]实现预测控制器的设立；

（4）利用设计好的最适控制器计算当前时刻的控制增量和预测输出值；

（5）计算控制量，并计算最适切换方法中需要各种值，将值以及控制量运用于被控系统中进行调试，找出最适的值，然后重复步骤（2）。

为了使模型切换过程产生的波动小，容易监控，故使用非线性强度度量值最小的输出偏差作为不同层次间模型切换的标准。

采用文献[8]中的方法，对各通道的非线性强度进行度量。在时间为t时，测量非线性强度较弱通道的输出偏差eout(t)。当eout＞a（a表示闭值）时，采用相对于该非线性强度弱的上层模型，在上层模型中，选择最适匹配模型运用到控制系统中。

其中，yout(t)为实际输出，yset为期望输出值。

当eout(t)≤a时，通过使用相对于该非线性强度弱上层次中最适匹配模型和该层次中最适匹配模型来计算控制量加权方式得到控制器输出，计算过程为：

①分别对输出通道i（i=1,， ...，ny，ny表示系统输出的个数）在上层模型中取恰当的子模型Mu,i（最适合模型），计算当前时刻的模型输出，并核准该子模型的输出偏差：

②分别对于输出通道i(i=1......ny)，在下层模型中选择恰当实用的子模型Mb,i(最适合模型)，计算当前时刻的模型输出yb,i,m，并核准该子模型的输出偏差：

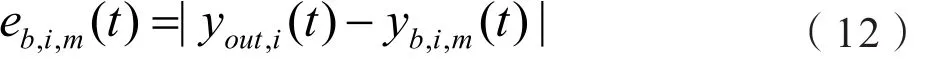
其中eb,i,m(t)为输出通道i选定的下层子模型的模型输出偏差，yb,i,m(t)为输出通道i选定的下层子模型的模型输出。

③从所求的Mu,i(i=1,…,)和Mb,i(i=1,…,ny)来说,应用GPC算法分别得到控制增量和。

④计算权重

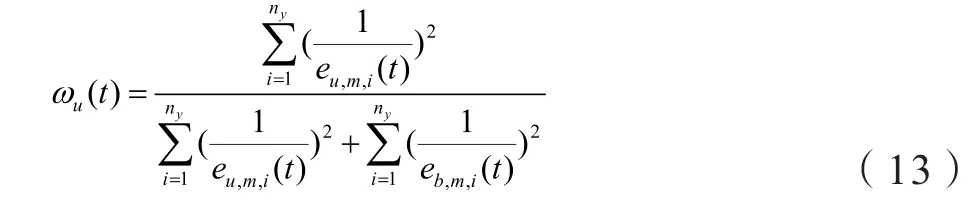
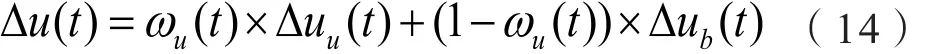
在Lj层，根据时间为t时工况数据与Lj层聚类中心的距离，判断t时刻的Lj层最合适模型。实际过程如下，假设风能转换系统聚类所用的工况数据集l是数据集合的属性个数，Lj层共有Kj个模型(即Kj个类)，cLj,m（m=1,2,…,Kj）为第m个运行中心。

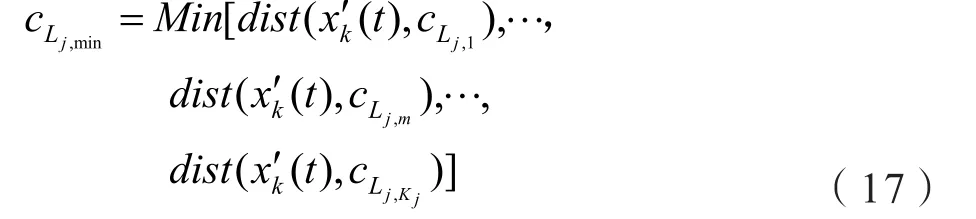
所求得的子模型就是该层最适合模型。

3 仿真实验

风能转换系统是一个复杂性很高的非线性系统，我们就按照控制策略理想的仅考虑一个扰动Vm两个设定值 桨距角β电磁转矩T为输入，高速轴转速ωg发电机功率Pg为输出。子模型输入与输出的关系式如下：

在仿真过程中，通过取得系统运行过程中的动态数据集合，然后通过建模方法获得多层次多模型(MHM)。系统的控制对象主要针对桨距角与电磁转矩，故针对性的把模型分为上层模型(TM1)跟下层模型（TM2），TM1有3个子模型，TM2有5个子模型，而且针对TM1和TM2的控制器参数也不同，参数见表1，其中m是控制时域，P是预测时域，w是控制权矩阵的系数，q是误差权矩阵的系数。为了更好的观察风能转换系统切换是的扰动，风速用阶跃风来分析。Vm作为平均风速，分别为7.5m/s、10m/s、16m/s。并且分别在50s、100s 出发生切换，就在切换时发生扰动。风速情况如图5所示。

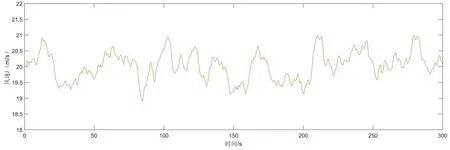
图5 不同时间段的风速Fig.5 Different periods of wind speed

表1 不同结构模型的控制器参数Table 1 Controller parameters of different structural models

首先，采用二次分段线性系统的稳定和控制[9]的方法，上下层输出通道采用各自对应的输出偏差作为层次间模型切换准则。系统通道的层次间子模型切换准则的闭值为0.35，Pg通道层次间模型切换准则的闭值为0.72。当层次间模型切换准则大于闭值时，采用上层模型，如果小于闭值时采用下层模型。在同层模型的切换采用基于K-means聚类的硬切换方法，同时利用多变量GPC算法设计控制器。

表2 风能转换系统过程中的参数[13]Table 2 Parameters in the process of wind energy conversion

将本文提出的多层次多模型预测控制切换方法(MHM)应用于系统中，并与传统的单层次多模型控制切换做比较，其中风能转换过程中的参数见表2，仿真结果的出如图6所示。

从仿真结果中可以看出，当系统的工况发生切换变化时，会产生明显的扰动。用单层多模型预测控制仅仅针对上层模型时，系统实际输出产生震荡比指定的值高的多，但趋向稳定时间较短;而单独采用单层多模型预测控制针对下层模型时，系统实际输出产生振荡就比较小，但趋向稳定时间就较长。采用多层次多模型模型预测控制，在工况发生切换的开始时刻主要针对上层模型，使得系统的实际输出快速。当eout达到闭值时，针对性的用硬切换思想，对和进行加权得到系统的控制量，大大减小了模型切换时引起的输出振荡，控制了震荡超调情况。

4 结论

本文通过分析风能转换系统运动时的特性，在理想控制的基础上，分析风能转换系统的运动数据，用闭值来判断系统在时间t为何值时进行层次切换，用层次间的控制量加权方法来实现降低系统输出时因多层次多模型切换引起振荡引。并且通过此切换方法对风能转换系统进行控制。仿真结果表明，该方法可以有效地解决风能转换系统的非线性系统工况切换时引起的波动情况，并且克服了层次与层次层次与子模型子模型与子模型切换过于频繁及模型切换本身给控制稳定性带来的影响。

图6 风能转换过程的仿真Fig 6. Simulation result of the multi-level multi-model predictive control of wind energy conversion system