基于Dijkstra算法的开放小区对周围道路的影响研究

牟菡子，王加慧，张宇恒，吴宇航

(1. 华北理工大学理学院，河北 唐山 063009；2. 华北理工大学以升创新教育基地，河北 唐山 063009；3. 华北理工大学信息工程学院，河北 唐山 063009；4. 河北省数据科学与应用重点实验室，河北 唐山 063009；5. 唐山市数据科学重点实验室 河北唐山 063009；6. 华北理工大学 数学建模创新实验室，河北 唐山 063009)

0 引言

建立合理的评价指标体系用来评价开放小区对周边道路通行的影响。首先分析出可以衡量道路通行状况的指标，得到道路车流量、道路行人量、自由流速度、红绿灯数量、路网密度、排队长度和通过平均时间七个评价指标，对初步选定的评价指标采用条件广义方差极小法选取在评价过程中作用较大的评价指标建立评价指标体系，方差大于域值的指标为道路车流量、道路行人量、通过平均时间即为最终确定的指标。

建立模型研究小区开放对周边道路交通的影响，通过建立改进的Dijkstra模型，将小区或周围处理作为节点，利用上一步得到的评价指标将有向边赋与时间有关的权值，通过路网的被选择通过率加权求和到一条有向边上，求得开放小区前后的任意两目标点的最短时间，用于反应其对交通状况的影响。对研究的十个小区按不同情况分两类，得到两类小区权值求解公式为：

在以上模型的基础上，将小区分为环形直形两类，结合实际情况考虑小区进出口数量及主干道结构，通过分析其对车流的疏散或汇集情况以及拥挤度这一概念，根据第二问求出权值公式，赋予不同权值，对开放小区前的普通时段及高峰时段，开放小区后的普通时段及高峰时段分别进行求解，得到高峰时段环形小区改善道路通行条件好，普通时段直行小区改道路通行条件较好。

通过所建立的模型，分析一天之内不同时段开放或关闭小区对交通道路情况的影响，建立以优化时间，路径为目标的双目标优化模型。对比结果建立以时间路径为对象的双目标优化模型，并得到动态优化方案，据此提出针对性可操作性建议。

1 条件广义方差极小法确定评价指标

1.1 评价指标的初步确定

选取合适的评价指标，建立合适的评价指标体系，用以评价开放封闭式小区对周边道路通行的影响。

选取评价指标关键在于评价指标在评价过程中的作用大小。假定要从N个指标中选取一个指标来评价某事物，则应该选取其中最具有代表性的指标，但一个指标绝不能把N个指标的评价信息都反映出来，故可以采用条件广义方差极小法，反应不完全的部分就是这个指标作为代表产生的误差，选取的指标越具有代表性，误差就越小，重复这一过程，即可选择出若干个代表性指标。

首先分析出能够评价周围道路通行情况的因素，通过查询文献[8]和分析，得到七个评价周围道路通行能力的指标，分别为道路车流量，道路行人量，自由流速度，红绿灯数量，路网密度，排队长度，通过平均时间。给定p个指标的组观察数据：

其中给定17~xx的指标分别为：道路车流量，道路行人量，自由流速度，红绿灯数量，路网密度，排队长度，通过平均时间。

其中道路车流量为单位时间内通过某段路的车辆数量，自由流速度为路段在低交通量，低密度情况下机动车所能达到的行程速度；路网密度为在一定区域内，道路网的总里程与该区域的面积的比值[7]，排队长度为在道路通行不畅的条件下，车辆等待队伍长度。通过查找数据[5]，以北京市内十个小区为例，分析开放封闭式小区对周边道路通行的影响。

1.2 计算广义方差

所查询到的10个样本数据，相应用矩阵X表示，即：

计算均值：

计算方差：

协方差：

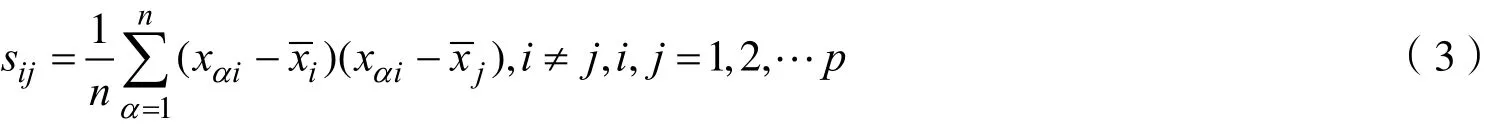
根据Matlab计算得到八个指标的条件广义方差如下：

表1 指标对应条件广义方差Tab.1 Index corresponds to conditional generalized variance

其中自由流速度、红绿灯数量、路网密度、排队长度的条件广义方差小于设定的阈值 1.50E-25，所以选择忽略，故而第一问选取的指标在不考虑小区内部结构的情况下为道路车流量，道路行人量，通过平均时间。

2 迪杰斯特拉算法求解

要求建立车辆通行的数学模型，研究开放小区对周围道路同行的影响，在此使用改进的 Dijkstra算法求解。确定研究对象为北京某区域，具体数据根据文献[6]得到，其中包括十个小区及路网如下。

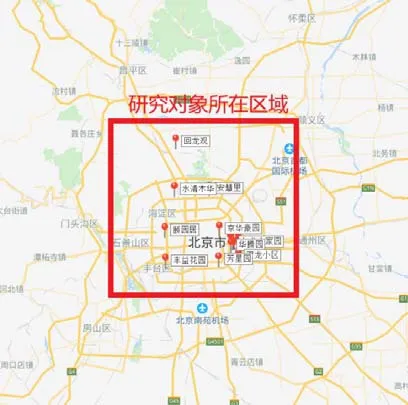
图1 研究对象分布图Fig.1 Distribution map of research objects

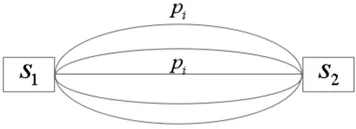
图2 主权边副权变关系Fig.2 The relation of sovereignty side and sub – contingency

将每一个小区抽象为节点，小区关闭后将小区周围的路口抽象为节点；将周围可通行的道路抽象为连接道路上各小区的有向边，查询地图能够发现每两个小区之间有多条道路可通行，为了求得更为准确的权边，以第一步得到的指标为基础对每一条可通行道路赋值，将这些道路以车辆选择通过率为权重加权求和，得到有向边的最终赋值。由于路径不能体现改变前后的准确情况，因为赋值与时间有关，可视化过程如下：

其中，s1、s2表示任意两小区或路口，Pi表示有向边权值，pi表示每一条通行道路的权值，车辆选择通过率为li，公式如下：

对于每一段的权值赋值，基于筛选得到的指标，得到其与通行时间的关系，由于每条路径之间的通行规则不同，例如路径间存在学校，学校附近路段限速等问题，所以会存在异常值情况，因此将所得值进行分类，并按照分类分别进行模型求解。

对于第一类数据，通过对散点图的拟合确定第一种分类为：京华豪园，双龙小区，安慧里，颐源居，水清木华，拟合结果如下：

图3 散点拟合图Fig.3 Scatter plot

其中，拟合度达到0.9899，SSE值为4.625e-05，结果可靠。

公式如下：

得到的第二类数据为：方星园，华腾园，九龙山家园，回龙观，丰益花园。拟合结果如下：

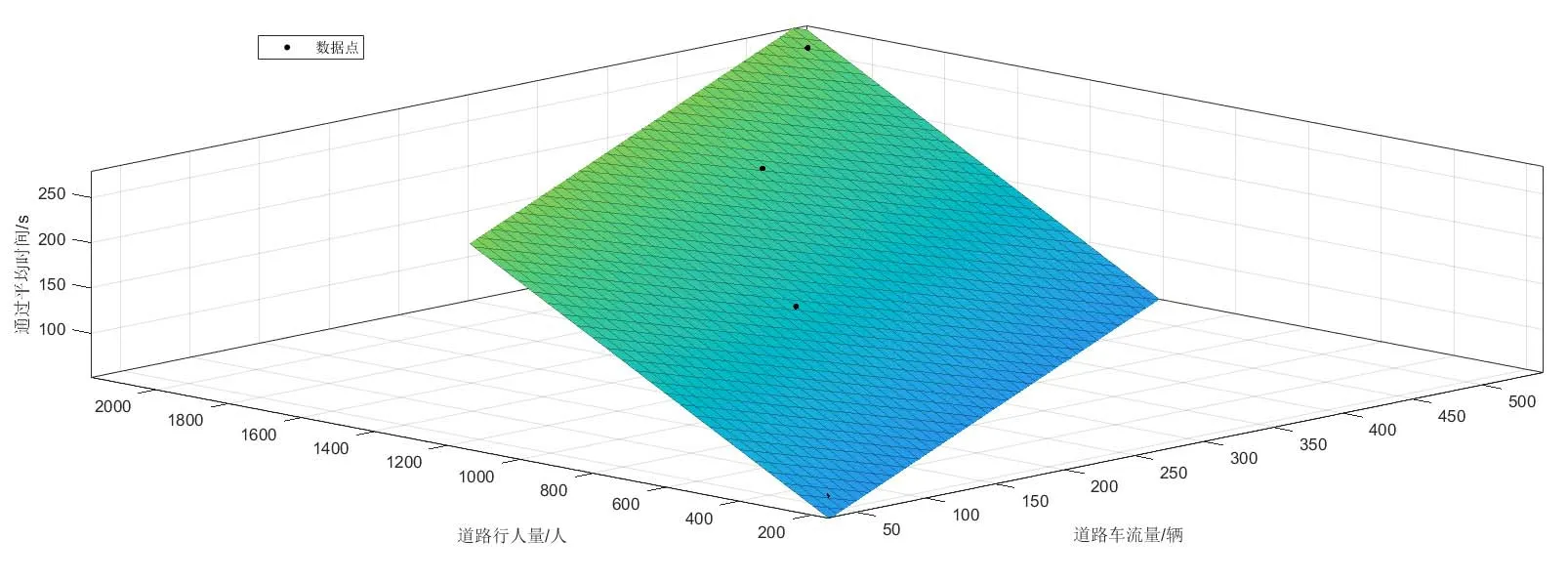
图4 散点拟合图Fig.4 Scatter plot

其中，拟合度达到0.9839，SSE为400.6，结果可靠。

公式如下：

其中：

通过以上计算公式，对不同小区之间的道路进行加权求和，得到权边赋值，结果如下，通过Matlab赋值求解：

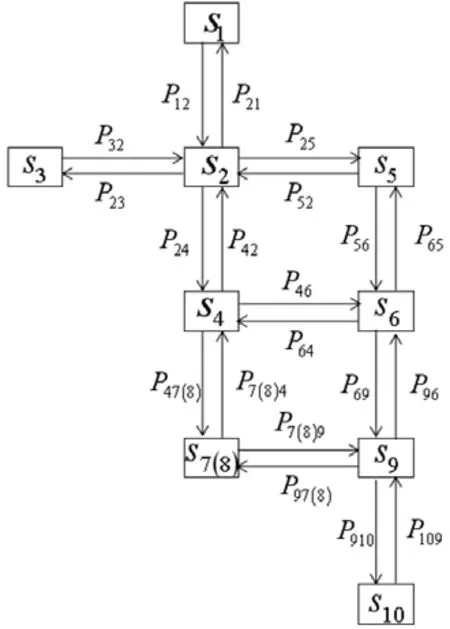
图5 抽象节点图Fig.5 Abstracts the node diagram

3 小区开放结果模型建立与求解

3.1 思维导图

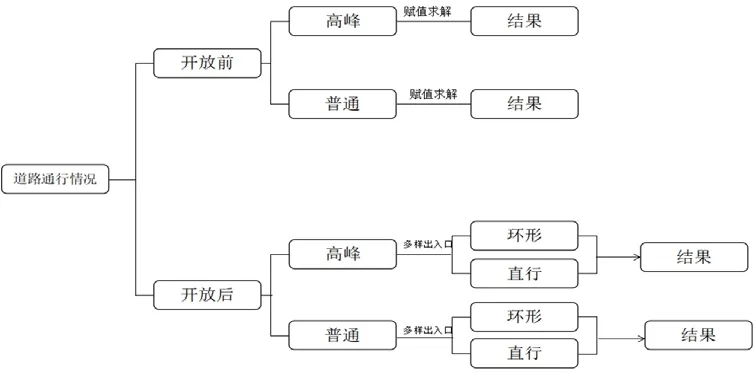
图6 流程图Fig.6 Flow chart

3.2 模型的建立与求解

基于得到的模型，考虑不同类型的小区,包括单入口单出口，多入口多出口，单入口多出口，单出口多入口对分散周围道路车流以及对交通路网的影响；主干道为环形结构以及直行结构对拥挤度进而对通行速度的影响和车流量分散效果。

对于前者，引入等价节点[3]这一概念，通过与时间相关的权值的相应减少或增加表示对车流量的分散和集中效果；

对于后者，由于在周围道路车流量不高时，直行结构小区的单位时间通过率要高于圆形结构小区,由于直行结构小区主干道为直线，在相同速度的情况下，单位时间内通过的车辆数量多，所以单位时间内停留在小区内的车辆少，故拥挤度较低，环形小区主干道为环形，在交通量高时有疏散车流的效果，故拥挤度低。

单位时间内停留在小区的车辆数量少，故而在某一周围道路车流量阈值之前，圆形结构的小区拥挤率高于直行结构小区，在某一阈值[1]之后，随着周围道路车流量增大，圆形结构小区作为通过道路起到了分流疏散的效果，类似于路口转盘，此时圆形结构小区的拥挤率低于直行结构小区的拥挤率。

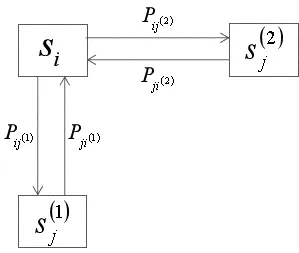
图7 等价节点表示图Fig.7 Equivalent Node Representation Graph

图8 环形结构示意图Fig.8 Schematic diagram of ring structure

图9 直行结构示意图Fig.9 Straight line structure diagram

根据道路通行规则、小区内道路宽度、小区内车流量及周边道路车流量进行定性分析得出的关于环形小区与直行小区拥挤度公式：

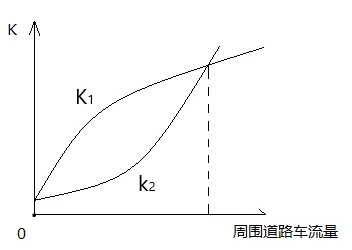
图10 小区内拥挤度与外部车流量关系图Fig.10 Diagram of the relationship between the crowding degree in the community and the external traffic flow

公式定性分析结果可视化：

结合上述方法，对查询[2]到的不同类型的小区信息数据进行处理，分析各小区信息如下表所示：

表1 小区信息表Tab.1 Cell information table

3.3 模型的结果分析

通过上述赋值方法，结合数据[4]对研究对象分高峰时段与普通时段对小区开放前后进行求解，并对Matlab求解的量化时间结果进行可视化表出，结果如下：

由图分析，在交通量较低，路面情况良好的普通时段下，小区的开放提高了路网密度，缓解了交通压力，提高了行驶效率，故而普遍开放小区时行驶时间较短。

由图分析，部分小区由于结构不够，例如多入口单出口结构小区，会造成车辆堵塞，在交通量高的情况下开放此类型的小区起到了反效果，但大多数的小区表现出了疏散车流，提高路网密度，缓解交通压力提高行驶速度的效果，故而大部分情况下开放小区会使得交通路况在高峰时段压力缓解。

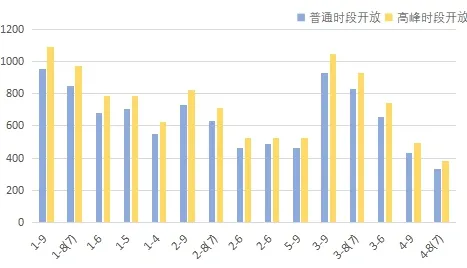
图11 普通时段开放关闭小区效果Fig.11 General period of time to open and close the community effect

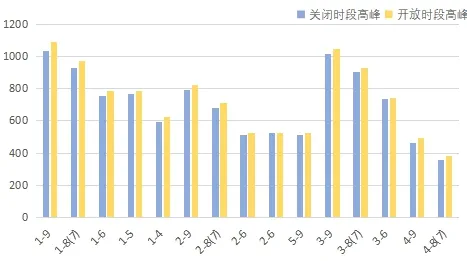
图12 高峰时段开放关闭小区效果Fig.12 Opening and closing the community during peak hours

4 小区开放的合理化建议

基于第三问的求解结果，建立以优化时间，路径为目标的双目标优化模型。其中：

基于第三问的启发，重点分析一天之内不同时段开放或关闭小区对交通道路情况的影响，可视化结果如下：

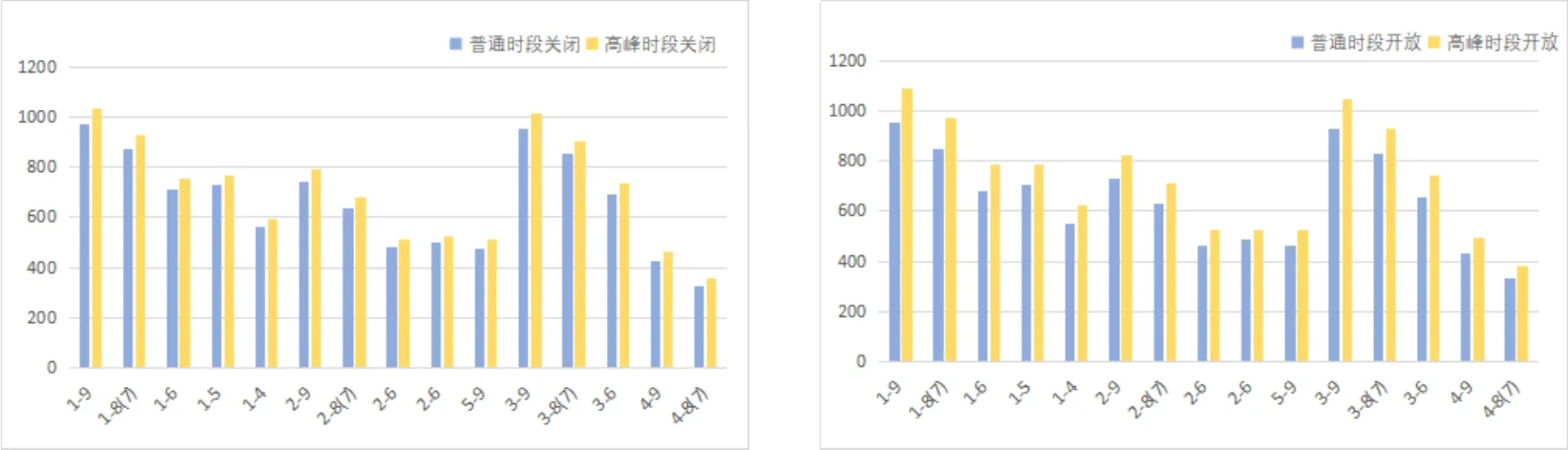
图13 一天内不同时段开放关闭小区效果Fig.13 The effect of opening and closing the community at different times of the day

据图分析，由于不同类型小区的构造，例如多入口单出口类型在高峰期会起到反效果，故而不宜选择在高峰期开放，但在大体上开放小区对交通道路情况的影响利大于弊，故而需要在一天内根据不同的时段有选择的开放和关闭不同类型的小区。针对此种情况得到如下优化建议：

（1）在高峰时段，可以选择定时开放环形结构小区，多进出口或者单进多出结构的小区，达到疏散车流，提高路网密集度，降低拥挤度，以提升通行效率避免堵车情况的发生。同时限制开放多进单出小区，以防在小区出口处堵塞。

（2）在普通时段，道路通行状况良好，可以选择开放单进单出小区或者直行结构小区在提升路网密度的条件下，提高通行车辆效率。

（3）对于多进单出结构的小区，由于其可以汇聚车流，且在数值上表现出对交通运行的负面情况，应尽量关闭此类结构小区或者在此小区路口加强管制和监督。