基于空间滤波的月球软着陆避障方法

彭杨杨，朱英豪，田 冰，吴宇航

（1. 华北理工大学数学建模创新实验室，河北 唐山 063009；2. 华北理工大学冶金与能源学院，河北 唐山 063009；3. 华北理工大学以升教育创新基地，河北 唐山 063009；4. 河北省数据科学与应用重点实验室，河北 唐山 063009；5. 唐山市数据科学重点实验室，河北 唐山 063009）

0 引言

月球探测是航天技术发展水平的象征，是国家综合国力的体现。在月球软着陆过程中，为使探测器安全抵达月球表面，它必须具备识别并躲避障碍，寻找最优降落地点的能力。王大轶等从图像中心开始螺旋前进搜索直到找到安全着陆区[1]，吴伟仁等利用光学平面图像完成粗略障碍识别，采用精细三维识别和中心螺旋搜索法确定着陆点[2]。占日新等建立局部环境模型，应用模糊识别对障碍物进行分类躲避[3]。该项研究提出采用空间滤波优化模型对着陆区域进行全局搜索，经粗避障细避障精化细分去除不合理点，得到探测器最优安全着陆点。

1 月球软着陆简介

月球软着陆过程共分为六个阶段，为保证嫦娥三号能够准确地在预定区域实现软着陆，着陆轨道与控制策略的设计十分重要[4]。探测器从着陆准备轨道经主减速阶段、快速调整阶段、粗避障阶段、精避障阶段、缓速下降阶段、自由落体阶段后抵达月球表面[5]。在粗避障阶段，探测器需要通过对拍摄到的数字高程图进行分析，避开月球表面大的陨石坑。在精避障阶段，探测器需要分析距月面更近的三维数字高程图，寻找最优降落地点。

2 软着陆过程避障方法

以嫦娥三号软着陆为例，对其软着陆过程中粗避障、细避障阶段进行研究。

2.1 粗避障段

探测器在距离月球表面2400 m时，对下方的月球表面进行拍摄，利用MATLAB对拍摄的图片进行三维优化处理后，再将该图转化为数字矩阵并将其进行矩阵分块，局部矩块进行相对拟合后得到图1：

三维差值拟合图可以更清楚的反映出开阔区域的起伏，对月球表面的坑洼地带的落差也有较好的描述，虽然图像在拟合后部分坑洼地带落差会产生微小变化，但由于矩阵分块较小，误差较小，图中的相对高度仍未发生改变。在着陆区域地形有较大的变化时，为避免盲目着陆带来的危险，做出该区域内的等高线图，如图2。

在等高线图上可以清晰的看出该地形区有较多的平坦区域适合嫦娥三号着陆。相对来说，平坦区域越大更能减少降落时的危险系数。下面通过空间滤波优化模型，并在算法中增加局部搜索策略提高搜索精度[6]，对着陆区域进一步进行精确求解。

图3为飞船在距离月球2400 m高空时的海拔分布图，下图中海拔越高的波动柱代表波动的越剧烈,危险系数也相应较高，该图为2300*2300的范围图。

图2 月球表面等高线图Fig.2 Contour map of the surface of the moon

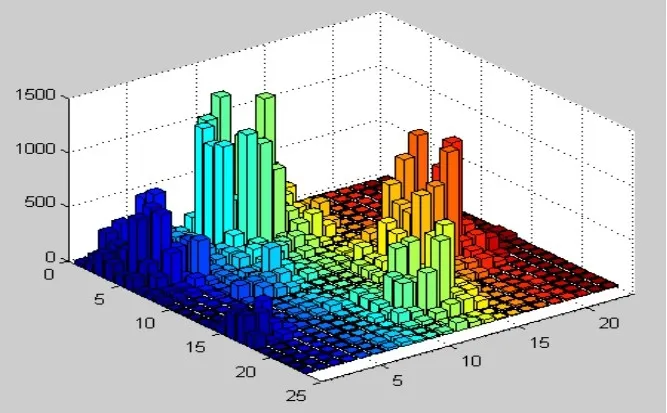
图3 月球表面海拔分布图Fig.3 Elevation distribution of the surface of the moon

在此图中按比例将原图缩放，将其分为23块，每一块区域所覆盖的月球表面范围为100*100。通过导入原图的数字矩阵并求取每块区域的方差来观察其波动情况，方差越小表明该区域越稳定。方差的波动情况即为区域的波动指标P，每个区域由矩阵的分块来决定。其计算公式为：

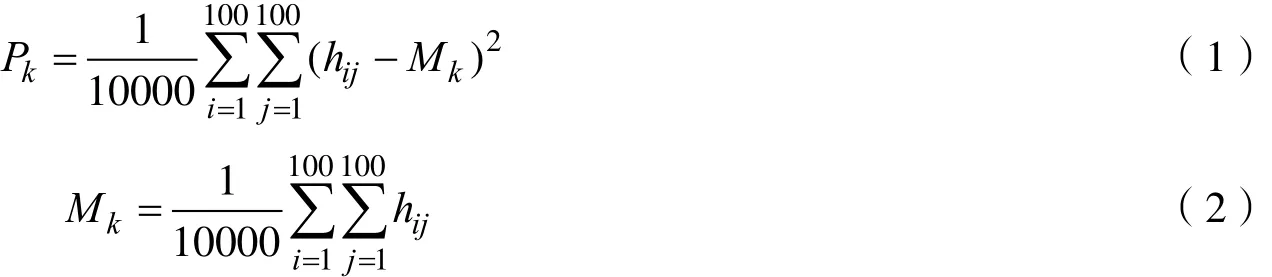
其中Mk为相应区域各点的平均高度，hij为（x，y）点的高度，Pk为相应区域的波动指标。矩阵大小规定为10000个点，根据每个点的高度，由公式计算各个区域的相对波动指标P。

以下为部分方差计算结果：

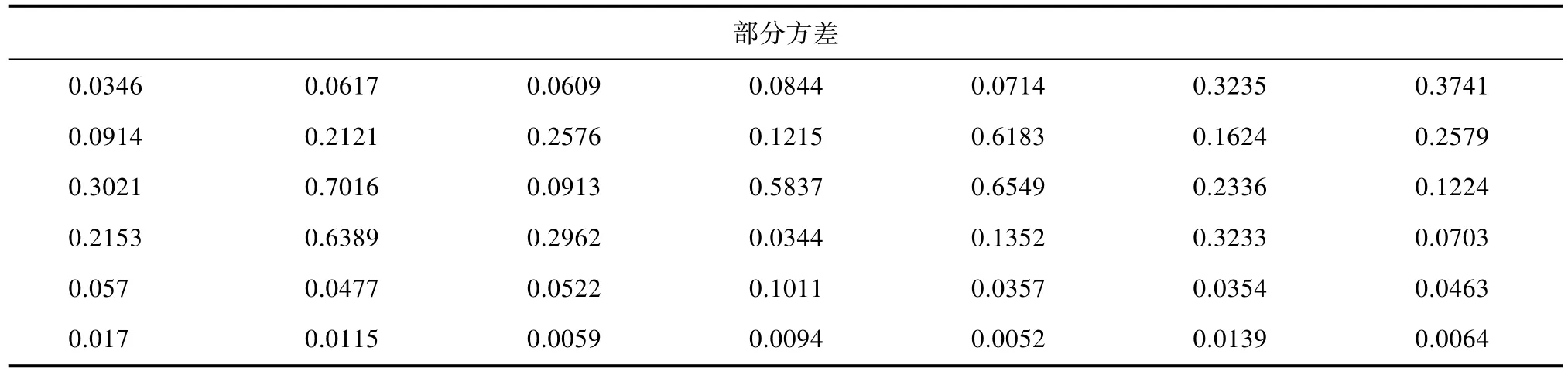
表1 部分方差结果Tab.1 Partial variance results

在此阶段利用螺旋搜索法，首先将嫦娥三号拍摄的图像转化为 2300*2300的数字矩阵，将大矩阵划分为小矩块后，求每个矩块的数字平均值并均分到小矩块中的每个元素点，为确定安全的着陆点，现对整块区域进行螺旋搜索，对于原来未分割的大数字矩阵中的每一块小区域的波动指标进行螺旋搜索，将高于平均值的元素点进行初步过滤，且在每次移动的距离大小可根据栅格间的距离来确定，当栅格间的距离较小时，每次移动一个或多个栅格。

通过对波动指标的求解，利用MATLAB进行螺旋搜索法进行筛选，将波动指标不稳定的区域排除，并将排除区域标记为黑色区域，即为不可降落点。图4为部分不可降落点的侧面剖视黑化图，对得到可降落的区域进行进一步分析，求出最合理的着陆地点。根据等高线初步分析选取（200,2000），（400,1600），（1600,2000）为着手点，根据空间仿真后选取（200,2000）为目标范围[7]。

图4 波动不稳定区域的侧面剖视图Fig.4 Profile view of undulating unstable region

2.2 精避障段

在嫦娥三号降落到距离月球100 m处时，对下方的月球表面100 m*100 m范围内进行探测拍摄，利用MATLAB对获得的数字高程图进行三维数字化处理，得到更加立体的图5。

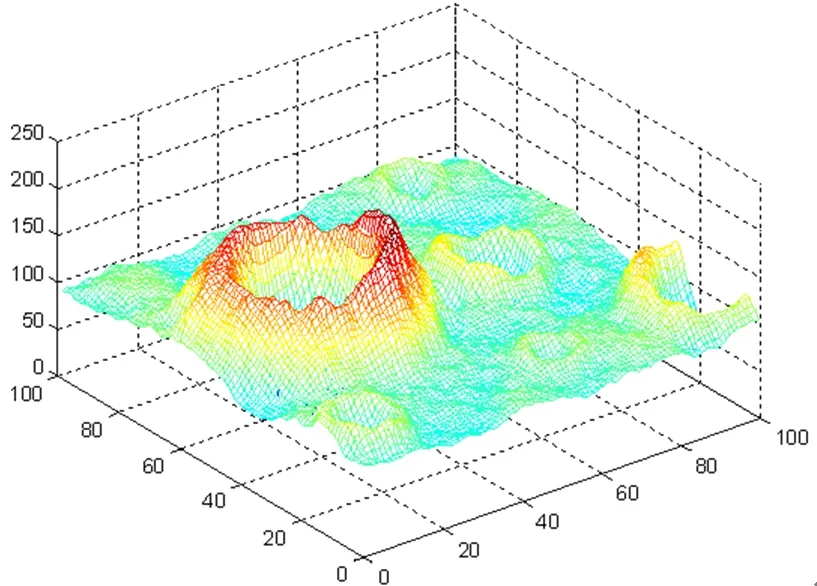
图5 三维数字化后的立体图Fig.5 3d digitized 3d image

通过观察可发现100 m时的地表波动情况没有2400 m时的地表波动情况那么剧烈，但也存在不可忽略的地表起伏，故不能随意降落，同时也可以明显发现嫦娥三号正下方存在着一个面积较大的环形山，应该尽量避免落入此环形山内，最为理想的着陆地点应为环形山与凹陷地区之间的平坦区域。为准确的确定着陆区域，首先做出地表波动图，如图6。

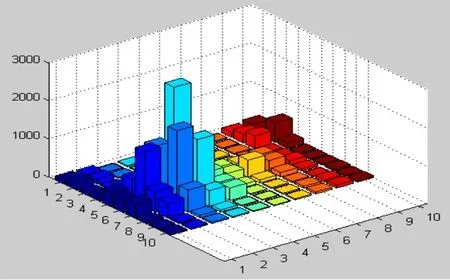
图6 地表波动图Fig.6 Surface fluctuation diagram

以嫦娥三号的投影点为坐标原点，建立三维坐标系，将整个区域划分为10*10的100个小区域，每个小区域有10000个点。依然采用上文中建立的空间滤波优化模型，对第一次过滤后的区域进行二次过滤，同样利用波动指标表示其波动情况，计算每个小区域内的方差，排除不稳定的波动指标所代表的区域。

二次方差计算部分结果如下：

表2 部分区域方差值Tab.2 Partial regional variance values

根据矩阵分块与图像分布的规律，找到波动最为稳定的点，即为着陆点。如图7，在以嫦娥三号投影点为原点所建立的三维坐标系中，着陆点的坐标为（226,189）。

3 结论

（1）粗避障阶段：以探测器的正投影为原点，其所在的竖直方向为轴，以底面的水平方向与竖直方向分别为x轴、y轴建立坐标系。对拍摄的数字高程图进行相关的图像处理，最终通过空间滤波模型的优化，排除一部分不可降落点，为之后的精避障做铺垫。

图7 最优着陆点坐标图Fig.7 Coordinate diagram of the optimal landing point

（2）精避障阶段：在距离月球表面100米处，通过对二次空间滤波模型的优化，可以得到更加平稳的最优降落区域，在所建立的三维坐标系中的坐标为（226,189）。