基于改进粒子群优化的BP神经网络对英文字符的识别

金姝含，张华钦，徐 滨，吴宇航

(1. 华北理工大学理学院，河北 唐山 063210；2. 华北理工大学机械工程学院，河北 唐山 063210；3. 华北理工大学数学建模创新实验室，河北 唐山 063210；4. 河北省数据科学与应用重点实验室，河北 唐山 063210；5. 唐山市数据科学重点实验室，河北 唐山 063210)

0 引言

当前，光学字符识别技术即OCR技术。由于其应用的广泛性，受到越来越多的关注。在印刷体的英文字符识别[1]当中，条形码的识别、车牌照的识别、图像的识别，成为众多学者探究的重要课题。本文将利用公开的光学字符数据集，研究26个英文大写字符的识别。对于英文字符的识别，现有的识别方法有很多,例如基于使用模糊推理的方法，基于神经网络的方法等等。查阅文献得到[2]，研究学者提出了人工神经网络算法来进行英文字符的识别，但由于神经网络算法有时不收敛,或陷入局部震荡,这就导致了识别率的下降。为此,本文研究了一种基于改进粒子群优化的 BP神经网络算法用于英文字符的识别[3]。这种算法利用改进后粒子群算法来优化BP神经网络中的阈值和权值，避免了陷入局部最优的状况，加快了收敛的速度，提高了识别率的准确性。

本文首先研究了神经网络算法用于英文字符的识别，然后研究了将蒙特卡洛方法用于粒子群，寻找全局最优值。再将改进后粒子群优化BP神经网络权值和阀值，并利用改进后的BP神经网络，用于26个大写字母的识别实验，实验表明，本文的研究方法具有准确的字符识别效果。

1 BP神经网络

BP神经网络是一种误差前向传播的多层前馈网络。传统的三层 BP神经网络[4]的拓扑结构如图 1所示，有输入层、隐含层、输出层组成。输入、输出转移函数由层间的转移函数所决定。层间转移函数由网络参数即单元的权值所决定，网络参数通过学习训练确定。

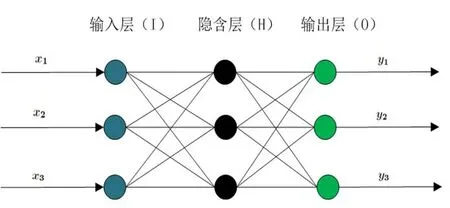
图1 神经网络的拓扑图Fig.1 Topology diagram of neural network

假设输入层含n个节点，隐含层含p个节点，输出层含m个节点，输入层到隐含层的权重记为ω>ij，偏置记为aj，隐含层到输出层的权重记为ωjk，偏置记为kb，学习速率为η，激励函数为g(x)。其中激励函数g(x)取Sigmoid函数：

隐含层输出记为Hj：

输出层输出记为Ok：

期望输出记为Yk，令Yk-Ok=ek，误差记为E：

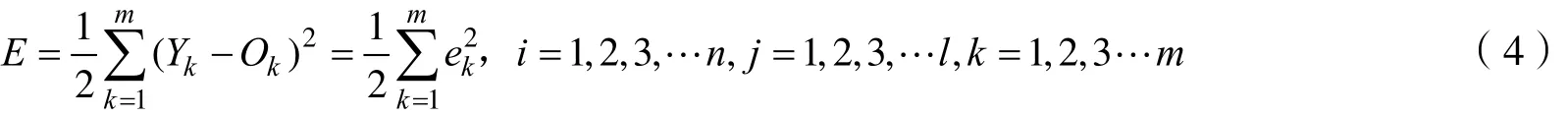
BP神经网络在传递过程当中，具有信号前向传递、误差反向传播的特点，倘若在传递过程中，输出层没有达到期望的输出值，则自动转入反向传播，网络自身会根据预测出来的误差对阈值和权值进行调整，从而使神经网络的预测值不断地逼近期望的输出值[5]。在误差反向传播的过程当中，要尽可能得使误差函数达到期望的最小值，即minE，权值的更新公式为：

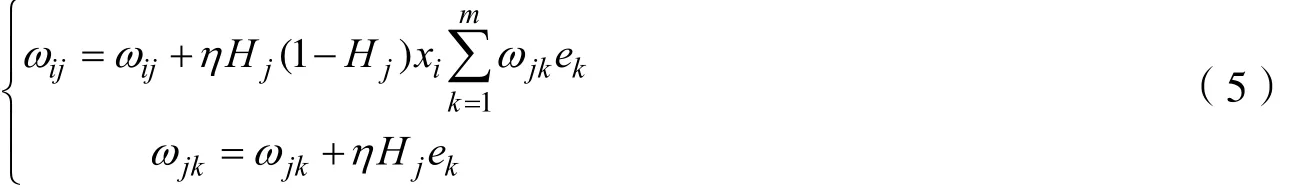
偏置更新公式为：

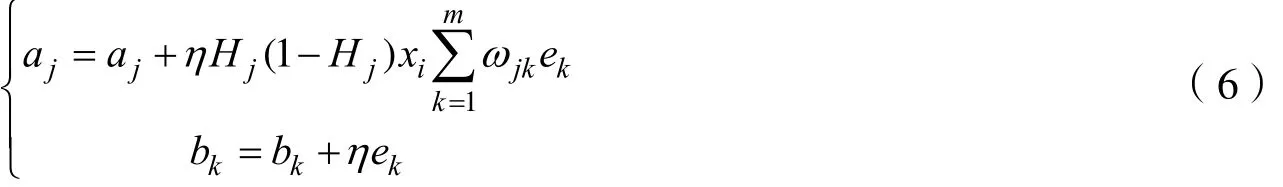
在上述变量及公式的基础上，建立BP神经网络识别模型，设定学习速率及训练次数，使输出层不断逼近期望输出值，当相邻两次迭代之间的误差小于指定值时，则说明达到识别结果，迭代停止。

2 粒子群算法

2.1 粒子群算法思想

粒子群优化算法[6]是由Kennedy博士和Eberhart博士于1995年提出的一种以族群动力学为基础的进化计算科学技术。它的基本概念来源于社会行为的模拟，每一个个体的行为不但会受到过去经验、认知的影响，同时也会受到整体社会行为的影响。

对应每一个个体在搜寻空间中各自拥有其方向和速度时，并根据自我过去的经验与群体行为进行搜寻策略的调整。其主要的优势体现在，粒子的收敛性快，算法易于实现，不受目标函数的梯度信息等影响，并且也没有许多参数要进行调整。

2.2 粒子群算法的基本步骤

（1）初始化设置微粒群的各项参数，随机选择初始粒子，计算各粒子的误差。

（2）比较群体中各个微粒的当前最小误差和群体历史最小误差，若当前误差更小，则令当前粒子位置为历史全局最优位置。

（3）比较群体中各个微粒的当前位置和群体历史最优的位置，保存误差小的成为历史全局最优位置。

（4）用（8）、（9）式对每个个体的位置、速度进行迭代。

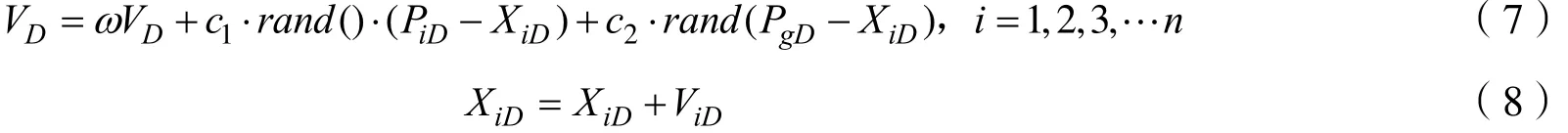
式中d表示第i个微粒所经历的历史最佳位置，Vi表示每个微粒的飞行速度，Pg表示在整个微粒群中，所记录的最佳解位置。参数c1以及c2分别是自我认知和社会模式的学习率。

（5）若系统的适应值误差达到设定的适应值误差限[7]，训练结束。输出历史全局最优位置即为所求神经网络的最佳权值和最优阈值。

3 算法改进

3.1 基于蒙特卡洛方法改进粒子群算法

为了避免粒子群算法陷入局部最优解，使用蒙特卡洛方法进行改进[8]。在粒子群算法得到最小值之后，扩大权值和阈值的搜索范围，重新选择初始点进行寻优。为了找到全局最优解，新的初始点尽量避开当前最优解，为达到该目的，按照卡方分布选取新初始点。

卡方分布的均值等于自由度，且随自由度的升高卡方分布逐渐接近正态分布。将卡方分布的这种特性用于粒子群初始点的选取，将卡方分布进行拉伸平移变换，使最优解对应卡方分布的均值，最大或最小值对应卡方分布的上分位点。各维度的变换公式如下。

其中，xchi是服从卡方分布的随机值；k是卡方分布的均值；p(α)是卡方分布的上α分位点；是该维度的极值，随机选取为最大值或最小值；xbest是当前最优点在该维度的值。

比较两个BP神经网络的预测误差，选择误差小的作为当前最优解[9]。如果新网络为最优解，将自由度a重置为初始自由度a0，再次选取初始点搜索最优解。如果旧网络仍为最优解，则使a增加1，再次选取初始点搜索最优解，这样，新的初始点的概率分布与上次不同，增大变异性，在自由度a达到最大自由度amax后，认为当前最优值即为全局最优值，结束算法。

3.2 基于改进粒子群算法的BP神经网络算法

（1）首先将神经网络的各个连接权值和阈值作为粒子群的位置向量，也就是说，将每一个神经网络的连接权值和阈值作为一个粒子群[10]，可用一个 T维的参数表示，则粒子群优化算法中的搜索空间维数为：

（2）给出一个BP神经网络进化的参数，将3.2.1得到的微粒ωi对BP神经网络的权值与阈值进行赋值，将训练样本输入，进行网络训练，得到一个神经网络的一个输出值j,则种群ω中个体ωi的适应值fiti可以定义为：

（3）在迭代过程中，根据（7）式和（8）式通过个体的极值和全局的极值，更新粒子自身的位置和速度，并引入蒙特卡洛的随机模拟，在粒子每次更新后以一定的概率初始化粒子。计算每个粒子的适应度值，根据新种群粒子的适应度值，更新粒子个体的极值和群体的极值。

（4）当满足最大迭代次数时，利用改进后粒子群算法[11]得到的最优粒子对 BP神经网络的连接权值和阈值分别进行赋值。将训练后的 神经网络识别模型进行26个英文大写字符的识别。

4 算法步骤

步骤1初始化各项参数。随机生成BP神经网络的初始权值与阈值n组，作为粒子群的初始点。

步骤2按照（7）式和（8）式寻找最优点，误差合格或达到最大迭代次数后停止寻找，得到当前最优解

步骤3将t的值增加1，按根据（9）式变换后的自由度为a的卡方分布随机生成BP神经网络的初始权值与阈值n组，作为新粒子群的初始点，进行步骤2。

步骤4比较两个最优解的误差，若当前最优解的误差更小，则淘汰新最优解，自由度a的值增加1；若新最优解的误差更小，则将新最优解的值赋予当前最优解，自由度a的值重置为初始自由度a0。

步骤 5重复步骤 3步骤 4，直到自由度后，认为当前最优解即为全局最优解，停止重复，按当前最优解对BP神经网络的权值和阈值进行赋值。

5 仿真实验

使用UCI的光学字符识别数据集对改进粒子群优化的BP神经网络识别模型进行测试。 UCI的光学字符识别数据集包含20000个样本，每个样本包含16个自变量和1个目标变量，随机选取2000个样本作为训练集，100个样本作为测试集。对比改进PSO-BP与BP神经网络和PSO-BP的测试结果，测试结果如下表。

表1 测试结果比较Tab.1 Comparison of test results

可见，改进后算法的准确率升高。表明算法的局部最优解问题得到了解决。如果对数据集进行降维处理，缩小搜索范围，会使准确率进一步提高。

6 结论

本文对蒙特卡洛算法、粒子群算法和BP神经网络算法三者结合用来对神经网络进行学习训练的方法进行了研究,并与BP神经网络算法和PSO-BP进行了比较。仿真实验结果表明,改进后的PSO-BP算法准确率最高,该改进大大降低了神经网络模型陷入局部极小值的可能、提高了模型的收敛速度和识别精度。改进后的粒子群优化算法作为一种有广泛适应性和具大潜力的优化算法可以在更多的领域得到应用。