基于烟气成分分析的转炉炼钢终点控制

高 聪，蔡晓桐，赵晓旭，吴宇航

(1. 华北理工大学 数学建模创新实验室，河北 唐山 063210；2. 华北理工大学 理学院，河北 唐山 063210；3. 华北理工大学 信息工程学院，河北 唐山 063210；4. 河北省数据科学与应用重点实验室，河北 唐山 063210；5. 唐山市数学科学重点实验室，河北 唐山 063210)

0 引言

随着经济技术的发展与生产力水平的提高，我国钢铁行业也迎来了新的发展机遇。由于占钢铁年产量近半的中小型转炉无法安装副枪系统，使得其在终点控制中的命中率较低，且面临着“去产能、绿色制造和市场竞争”的耦合压力。因此，突破中小型转炉炼钢的技术瓶颈，创建中小型转炉智能炼钢系统也变得尤为重要。

赵云珠等[1-5]研究表明：转炉炼钢是将铁水、废钢、铁合金以及一些副料通过高炉加热，通过复杂的化学和物理反应，将铁水中的硫、磷等对钢铁性能产生负面影响的元素进行置换，同时根据后续工艺要求获得符合产品性能条件的钢水的过程。其中，氧气转炉由于单炉产量大，吹炼时间短、热效率高、升温速度快等优点得到了广泛的应用。

由于在转炉冶炼过程中其反应过程极为复杂，影响因素也比较多，同一时刻会产生多种数据。由于冶炼设备质量、外界环境变化、操作人员习惯不同等影响，会在整个炼钢过程中产生大量冶炼数据，因此，对预测模型的数据处理方面提出了一定的要求。

在以往传统冶炼中，由于冶炼过程中存在的多元多相高温的反应，使得传统机理分析难以较为高效准确的预测出钢水不同时刻成分含量。Omran[6]提出根据多变量因子，建立以多元回归为基础的预报方法，但由于其方法简单，存在着预测精度不高等问题。Kurkin[7-8]等人提出将人工神经网络技术应用到转炉炼钢控制中，建立出基于人工神经网络的静态、动态和混合控制模型。该方法可在一定程度上克服常规线性模型的不足，进一步提高预测模型的控制精度，从而改善控制效果。但由于 BP 神经网络收敛速度慢，且容易陷入局部极值点的缺陷，使得其方法在实用性与准确性方面在冶炼行业没有得到较大的推广应用。

通过王景[11]等人对于组合预测方法的理论研究，本文创新性的将其方法应用于钢铁冶炼行业，对炼钢过程中产生的实时数据进行数据分析处理，结合回归模型与BP神经网络方法特点，消除和减少了两种方法局限之处，建立基于回归与BP神经网络组合预测的碳温组合预测模型。预测结果表明，组合预测模型效果优良且鲁棒性较高，大大提高了钢铁冶炼时碳温的预测精度。

1 基于回归与BP神经网络组合预测的碳温预报模型

1.1 多元回归分析法

1.1.1 多元线性回归的介绍

多元回归分析是建立在相关性原理基础上的处理变量之间相关关系的数理统计方法，通常包括多元线性回归，多项式回归，指数、对数回归[11-13]，现已经被广泛应用于社会、经济、技术以及众多自然科学领域中的研究中。

1.1.2 逐步回归方法确立模型

本文采用的是逐步回归的方法建立多元线性回归模型，逐步回归是消除自变量之间多重共线性的一种方法。

查阅文献[13]可知，预测转炉终点控制碳温系统的主要方法是根据烟气中CO和CO2的含量，以及耗氧量Q和耗氧量比PQ进行确定。

根据钢厂[14]提供的数据，利用SPSS软件进行相关系数的判定，发现[C]&[T]两个因变量分别与耗氧量比例PQ、氧气消耗总量Q、烟气中[CO]和[CO2]的含量四个自变量之间存在很强的相关关系，并且检验四个自变量之间是否存在多重共线性，根据检验结果利用逐步回归的方法建立模型，具体流程如图1。

图1 计算流程图Fig.1 Calculation flow chart

利用钢厂[14]提供的数据采用逐步回归的方法可计算得到[C]&[T]的线性回归模型为：

1.2 BP神经网络

1.2.1 BP神经网络的介绍

BP神经网络采用基于梯度下降和误差方向传播的学习方法, 其目标是使网络输出与训练样本的均方误差最小, 具有自学习和推广概括的能力, 特别适用于求解内部机制复杂的问题, 是目前较为成熟且应用最为广泛的人工神经网络[15]。

1.2.2 BP神经网络建立模型

设输入层有l个神经元，输出层有p个神经元，隐藏层有h个神经元，BP网络的实际输出是y；期望输出是 'y；实际输出与期望输出之间的误差函数ε为：

每个权值的修正值为：

其中：ωhj为输入单元到隐藏层单元的权重；η是学习速率，Ij是中间第j个隐藏层的传输函数。

设定氧气消耗比例-PQ、氧气消耗总量-Q、烟气中的CO含量-[CO]、烟气中的-[CO2]这四个因素为神经网络模型的输入参数，钢水中的碳含量C为输出参数。

由于神经元个数多容易产生过拟合，个数少则拟合精度降低，在确定神经元个数时，分别取值2、3、4、5、6，多次运行神经网络，观察拟合度R方的变化，发现当取值为3的时候拟合度最稳定，故取隐含层节点数为3个。

图2 神经元取值不同时刻拟合度变化Fig.2 Changes of fitting degree of neurons at different times

据此建立的BP结构为：

图3 BP神经网络示意图Fig.3 BP neural network schematic diagram

神经网络训练前，为减弱各输入因素不同量纲的数据对网络模型训练与预测值的影响，应先对输入因素做归一化处理。

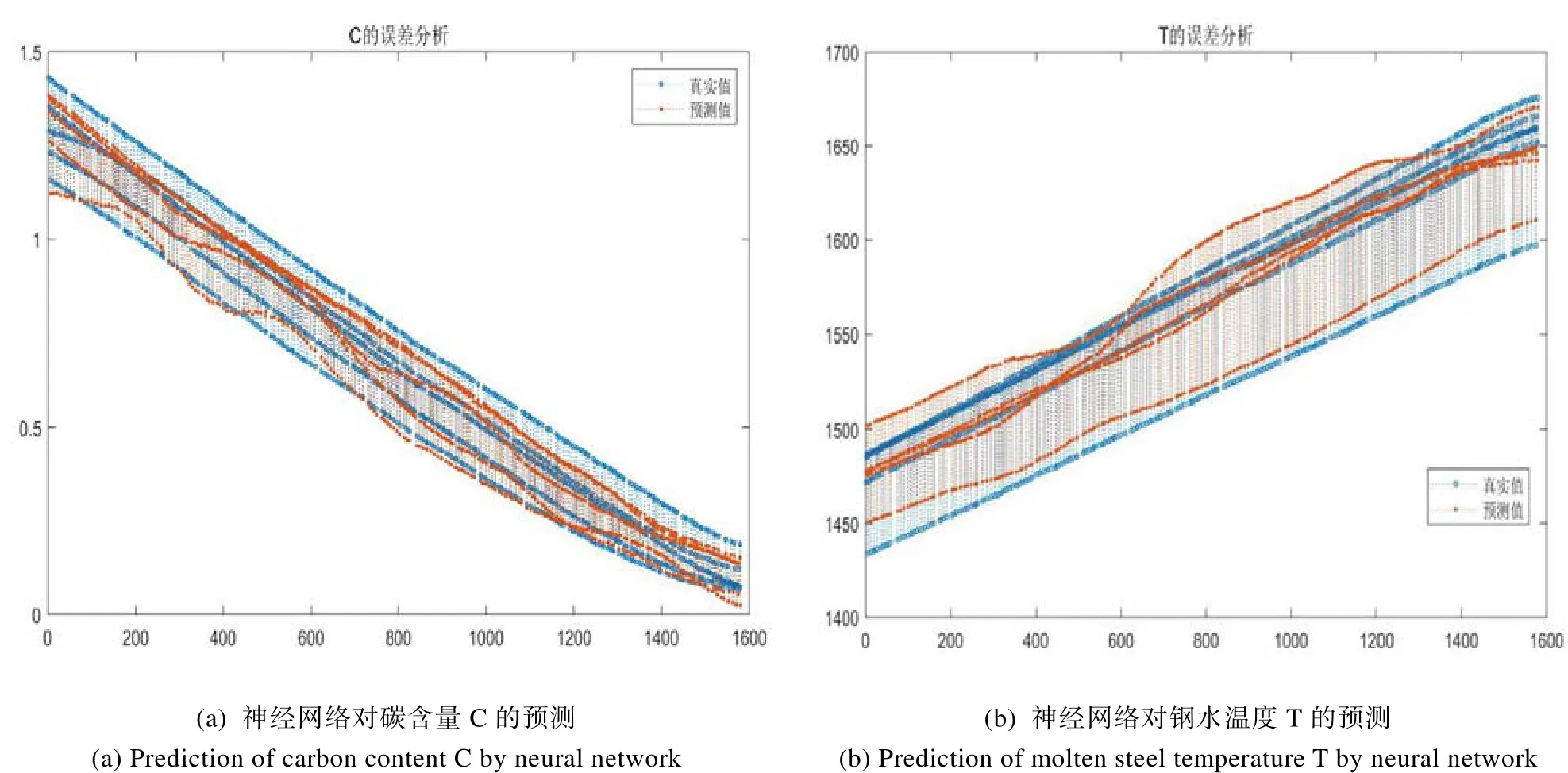
图4 神经网络模型的预测值与真实值对比Fig.4 Comparison of predicted and real values of the neural network model

1.3 组合预测的介绍

在预测实践中，对同一问题采用不同的预测方法，不同的预测方法提供不同的有用信息，其预测精度往往也不同，如果简单地将预测误差较大的预测方法舍弃掉，将会丢失一些有用的信息。一种更为科学的做法是讲不通的预测方法进行适当的组合，从而形成组合预测方法[11]，即，组合预测模型就是先利用两种或者两种以上不同的单个预测模型对被预测对象进行预测，然后利用某种准则对单个模型进行综合，形成组合模型，再利用组合模型进行预测。

1.3.1 组合预测的分类

模型I线性组合模型：

模型II加权几何平均组合预测模型：

模型III加权调和平均组合预测模型：

1.3.2 方差倒数加权法

方差倒数法称为预测误差平方和倒数法，一般对于每种单一预测模型来说，他们的预测误差都是不同的，预测误差平方和是反映预测精度的一个指标，预测平方和越大证明预测精度越差，因此，在进行组合预测时他的重要性就要降低，对应的权重就会减小。所以，令：

其中，Di为第i种预测的误差平方和，即，

1.3.3 组合预测模型的具体实现

本文采用方差倒数加权法对线性组合的多元线性回归以及BP神经网络预测进行加权，得到，关于[C]的预测组合模型BP神经网络的权重为 0.819，多元线性回归的权重为 0.181，将两种方法的预测值进行加权预测得到新的预测值，利用Matlab软件进行训练（附录）得到预测精度较为精准的[C]的固定区间为耗氧比例 PQ在72.16%~73.34%，预测模型为，同理可以得到[T]的组合预测模型为, 预测精度较为精准的[T]的固定区间为耗氧比例的固定区间为耗氧比例PQ为71.06%~74.27%。

用建立的C组合预测模型对数据进行预测，当真实值碳含量±0.05时，命中率达到81.52%

表1 [C]元素预测精度表Tab.1 [C] element prediction accuracy table

用建立的T组合预测模型对数据进行预测，当真实值钢水温度5±时，命中率达到69.94%

表2 组合预测精度表Tab.2 Combination forecasting accuracy table

2 结论

炼钢终点控制的重要环节是碳温控制系统，碳温动态预报模型尤为重要。本文利用回归BP神经网络组合预测的分析方法，确定了碳温预报模型。如果只使用多元回归分析的方法它的命中率达不到90%，只使用BP神经网络，它的精度同样达不到90%，因此，为求得高精度采用两个方法的组合预测，使精度可达到93%。本文的创新点有以下几点：

(1) 采用逐步回归分析法建立多元线性回归模型，消除了多重共线性造成的误差；

(2) 比较多元线性回归、BP神经网络和组合预测三种预测模型的精度，证明了组合预测模型效果最佳，鲁棒性较高。

符 号 说 明

ωhj——输入单元到隐藏层单元的权重

η——学习速率

Ij——中间第j个隐藏层的传输函数

PQ——氧气消耗比例

Q——氧气消耗总量

CO——烟气中的CO含量

CO2——烟气中的CO2含量