基于热弹流润滑的墨辊挤压接触区的油墨温度分析

初红艳 陈立博 安 然 蔡力钢

北京工业大学先进制造与智能技术研究所，北京，100124

0 引言

随着社会的发展，人们对印刷品的质量要求也越来越高。为了提高印刷质量，国内外学者进行了诸多研究。BHOOMKAR等[1]提出用“世界一流制造”(WCM)的方法来提高胶印机的印刷质量，采用油墨温度控制装置保持油墨温度恒定以保证印刷质量；ROBERT等[2]研究了现代柔性印刷机中温度对油墨黏性及油墨转移率的影响。目前，国内外学者对普通胶印机墨辊的热效应研究较少，而随着技术的发展，胶印机的印刷速度越来越高，在印刷过程中，随着印刷速度的提高，油墨、墨辊的温度也随之升高。温度能显著地改变油墨的黏度，进而影响油墨在墨辊间的流动与传递，因此对印刷过程中油墨的温升情况进行研究很有必要。

弹性流体动力润滑简称弹流润滑，它主要研究点线接触中弹性表面间的流体动力润滑问题，如接触区流体压力与流体通道厚度等。胶印机输墨系统中，在正常工况下，一软一硬两墨辊相互挤压对滚，油墨从墨辊间的墨路通道通过，软辊在挤压中发生弹性变形，且接触区相对较小，该模型可近似地看成一个弹流润滑系统，对接触区的温度分析需要用到热弹流润滑理论。

学者针对大刚度接触表面间的热弹流润滑进行了研究。王大伟等[3]在综合考虑载荷、速度及润滑剂热效应等影响因素的基础上，基于Ree-Eyring型非牛顿流体模型建立了滚动轴承热弹流润滑的数学模型，求得了压力、温度及油膜厚度的分布，探讨了速度、载荷、滚子半径等参数对滚动轴承润滑特性的影响；BRACCESI等[4]应用热弹流润滑相关理论分析了滚珠丝杠中的润滑油温度变化；武斌[5]建立了低速重载齿轮传动微观热弹流润滑的数学模型，并针对该数学模型中形式相当复杂的二阶非线性偏微分方程组的特征，运用多重网格法求解了接触区油膜的温升情况。

本文结合印刷机实际情况，对一软一硬两个接触表面之间的热弹流润滑问题进行详细研究。

1 热弹流润滑理论

热弹流润滑理论的研究对象是点线接触摩擦副中的热现象和热效应，包括接触区内油膜温度分布及温度场对压力分布、油膜形状与厚度等的影响。接触区内温度升高会使润滑剂的物理化学特性发生较大的变化，因此对接触区内温度场的研究意义重大。等温弹流润滑理论中忽略了热效应的影响，对于速度较小或滑动速度较小时的情况较为适用。当高速滚动或有较大滑动时，就必须考虑热效应所带来的影响。在求解热弹流润滑问题时，需在等温弹流润滑的基础上联立能量方程、热界面方程，即需联立求解雷诺方程、弹性变形方程、能量方程、热界面方程、运动方程。

1.1 雷诺方程

雷诺方程可描述狭小间隙中黏性流体的流动，是流体力学中Navier-Stokes方程的一种特殊形式。在线弹流润滑情况下，当润滑油在两固体表面之间进行层流流动时，所形成的油膜压力分布可由下式来描述：

(1)

式中，u为卷吸速度；η为黏度；p为油膜压力；ρ为润滑油密度；t为时间；h为膜厚；x方向为润滑油流动方向。

式(1)为线接触条件下的雷诺方程，适用于求解各种非稳态工况下流体润滑问题。

1.2 弹性变形方程

线接触问题通常可视为无限长柱体的接触。在胶印机的实际工况下，两墨辊接触区相对于墨辊长度特别小，因此适用于线接触问题。在无限平面上的任意分布力p(x)在M点产生的弹性变形δ(x)见图1。

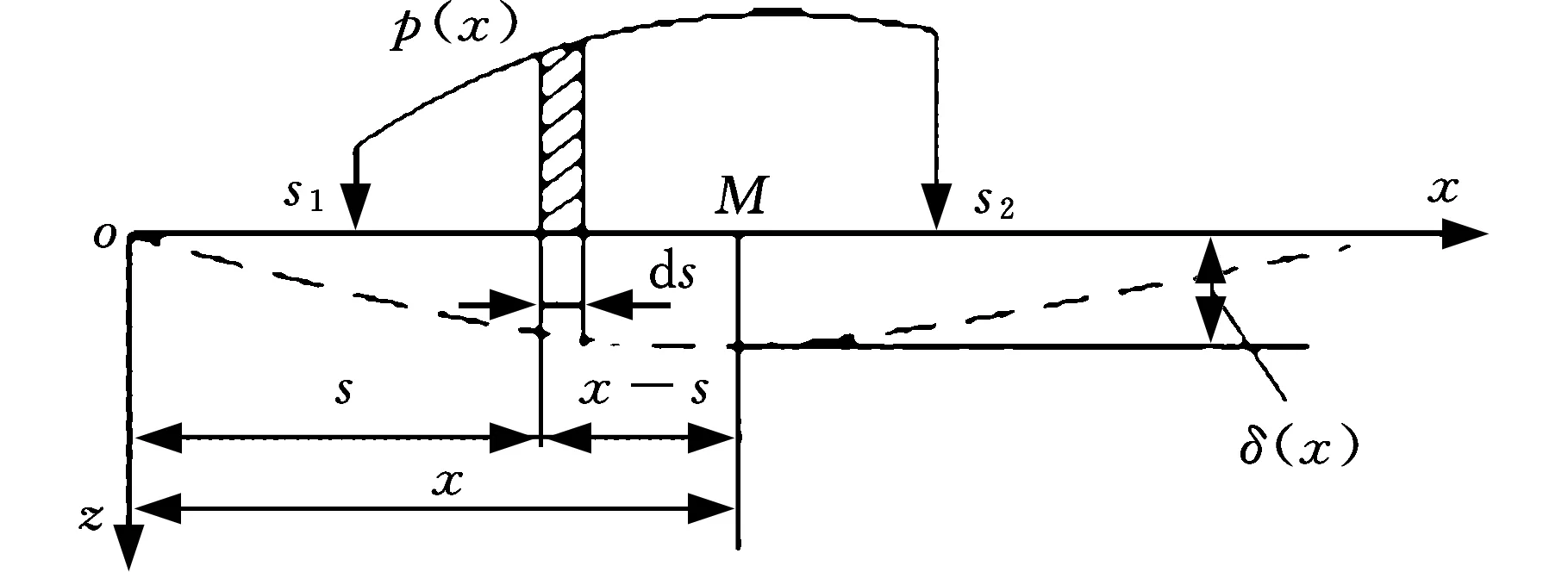
图1 分布力作用下的变形Fig.1 Deformation under the distributed force

在弹流润滑中，两个被润滑油膜隔开的表面都是弹性表面。由于受到油膜压力的作用，两表面受到数值相等而方向相反的法向分布力的作用，从而产生了弹性变形，将弹性变形与两柱体间隙厚度相叠加，就可得到线接触弹流问题的油膜几何方程(即弹性变形方程)：

(2)

式中，hc为中心膜厚，此时hc即为原点处的实际膜厚；E′为当量弹性模量；R为当量曲率半径。

1.3 能量方程

在热弹流润滑理论中，当发生高速滚动或滚动中伴有较大滑动速度时，就必须考虑润滑中的热效应和温度场的影响。在润滑过程中，油膜受到黏性剪切和压缩作用而发热，造成温度升高，同时，所产生的热量通过对流和热传导而散失，这样，就需要能量方程来计算润滑油膜的温度场[6]。

如果不考虑体积力和热辐射的影响，根据能量守恒定律，黏性流体流动时的能量方程有如下普遍形式：

(3)

(4)

式中 ，T为温度;cp为质量定压热容；Φ为耗散功；k为热导率；u、v、w分别为直角坐标系下流体沿x、y、z方向的速度；y为油膜流动法向；z为垂直于xy平面的方向。

(5)

1.4 热界面方程

在求解润滑膜的能量方程时，需要根据固体的热传导情况来确定润滑膜与固体相接触的界面上的边界条件。

一般形式的固体热传导方程为

(6)

式中，c为质量热容。

由于接触体处于运动状态，故接触表面的温度计算可以归结为具有移动热源的半无限大体的热传导问题。忽略x和y方向的热传导，最终可得两个界面上边界条件：

(7)

式中，K1、K2分别为两个界面的传热系数；T0为初始温度。

1.5 运动方程

在求解能量方程时，需要先确定润滑油膜的速度场，这时就需要根据给定的压力分布和油膜厚度来求解运动方程以确定速度场。

对于线接触问题，运动方程为

(8)

2 油墨温度场的热弹流润滑模型建立

2.1 方程的量纲一化

2.2 方程所需参数的确定

为了给下文油墨温度分析提供数据支持及分析载荷、速度、材料等参数变化对油墨温度的影响趋势，选取了包含实际工况参数在内的较大范围的参数。

在调节印刷压力时，往往以两辊挤压时的接触宽度作为判断依据，北人集团公司生产的某对开胶印机的串墨辊的推荐接触半宽为4～5 mm，根据有限元软件仿真模拟反推可知载荷力的大小约为100 N，本文取100～500 N的载荷范围。

在实际印刷过程中，正常的印刷速度为0.36～1.5万张每小时，对应的最小墨辊角速度约为10 rad/s，本文取10～30 rad/s的速度范围。

依据墨辊实际情况确定各项参数，两辊半径均为32.5 mm，上下两辊相互挤压对滚，见图2。

图2 挤压对滚模型Fig.2 Squeezing rolling model

实际工况中，胶印机的硬辊和软辊均采用钢制辊芯，但钢芯直径一般为墨辊直径的一半，本文重点分析墨辊挤压接触区的油墨温度，接触区距离钢制辊芯较远，所以忽略钢质辊芯的影响。设定硬辊(硬塑胶辊)弹性模量E1为4 GPa，泊松比μ1为0.33；软辊(橡胶辊)弹性模量E2为7.84 MPa，泊松比μ2为0.4。印刷油墨的初始环境黏度为42 Pa·s；印刷油墨的环境密度为1.5 g/cm3；通过实验测得，油墨黏压系数为2.57×10-8m2/N。橡胶的热导率为0.2 W/(m·K)，质量定压热容为1 600 J/(kg·K)，密度为1 050 kg/m3。塑料的热导率为0.12 W/(m·K)，质量定压热容为1 540 J/(kg·K)，密度为1 050 kg/m3。

2.3 方程的求解

与等温弹流润滑相比，热弹流润滑的基本问题是要根据能量方程求解润滑膜的温度分布，同时，在求解雷诺方程时，将黏度作为温度和压力的函数，而由能量方程可知，温度场的计算又取决于压力的分布和界面边界条件的确定，这样，在热弹流润滑的计算中，除去等温弹流润滑所需的方程外，还需要联立求解能量方程和热界面方程。

由于热弹流润滑数值计算的工作量巨大，故侯克平等[8]提出了热弹流润滑的简化求解方法，其基本思想是忽略热效应对压力分布和膜厚的影响，在等温条件下求得不同工况下弹流润滑压力分布和油膜厚度，然后在此基础上，直接通过求解能量方程、运动方程和热界面方程及润滑油的黏温方程来确定油膜的温度分布。

在计算时，由于能量方程中的温度、黏压温方程中的黏度及弹性变形量都随着压力变化，因此，首先应给出一个初始的压力分布，本文采用ANSYS软件计算所得的接触应力作为初始压力分布；其次，应给出一初始温度分布，本文采用数值等于室温的均匀温度场；计算黏度值后，代入能量方程求得温度，利用新的温度值修正黏度，反复迭代直至两次计算的温度差小于0.01 ℃，即可看作温度收敛。求解过程见图3。

图3 温度求解流程Fig.3 Temperature solving process

3 油墨层温度分析

3.1 接触区油墨层压力及厚度分布

代入载荷100 N进行运算，接触区油墨压力分布及油墨墨层厚度分布见图4。图4中，横坐标为接触区节点编号，接触区中心处在横坐标中70号节点所在位置，可以看出，油墨墨层压力最大值出现在接触区中心稍靠近出口处，最大值约为1.44 MPa。油墨墨层厚度在接触区前逐渐减小，在接触区内相对稳定，在近出口处出现了颈缩的现象，颈缩处油墨厚度最小，接触区中心墨层厚度约为0.073 mm。

(a)压力分布 (b)厚度分布图4 压力及厚度分布Fig.4 The distribution of pressure and thickness

3.2 接触区油墨层温度分布

沿油墨层厚度方向取5层，所得油墨各层温度分布见图5。

图5 墨层厚度方向各层温度Fig.5 Layers temperature

当只讨论油墨中间层温度时，可以看出随着油墨逐渐进入挤压区，油墨的温度不断升高，在接触区墨层压力较大的区域，油墨的温度变化也较大，最后随着远离最大压力区，油墨温度逐渐降低。这是由于高压力使得油墨黏度增加，从而能量方程中的耗散功一项增大，使得高压力区油墨温度的值也较高。

比较不同位置的温升，可以发现，中间层油墨温度最高，100 N时，中间层最大温升值为2.231 ℃，靠近两墨辊处的温度较低，塑料表面层最大温升值为1.851 ℃，橡胶表面层最大温升值为1.679 ℃。这是由于换热的影响，油墨所产生的热量传递给了两侧墨辊，从而导致了靠近墨辊处的油墨温度降低。比较橡胶表面层和塑料表面层的墨层温度，可以看出塑料表面层的温度更高，这是由于塑料的热导率较小，因此传播热的能力较低，这样，塑料表面就容易聚集较多的热量，从而产生较高的温升。

3.3 载荷对接触区温升的影响

保持其他参数不变，只改变载荷力大小，计算接触区最大温升，设定载荷分别为100 N、150 N、200 N、250 N、300 N，油墨中间层最大温升见图6。

图6 不同载荷下的温升Fig.6 Temperature rise under different loads

载荷增加即接触区的压力增大，随着压力的增大,油墨黏度增大，同时能量方程中的耗散功一项增大，因此，随着载荷的增大，油墨中间层最大温升提高，温升由载荷为100 N时的2.231 ℃，升高到300 N时的3.41 ℃ 。

3.4 速度对接触区温升的影响

保持其他参数不变，只改变两辊对滚速度大小，计算接触区最大温升，设定对滚速度分别为10 rad/s、15 rad/s 、20 rad/s、25 rad/s、30 rad/s，接触区油墨中间层最大温升见图7。

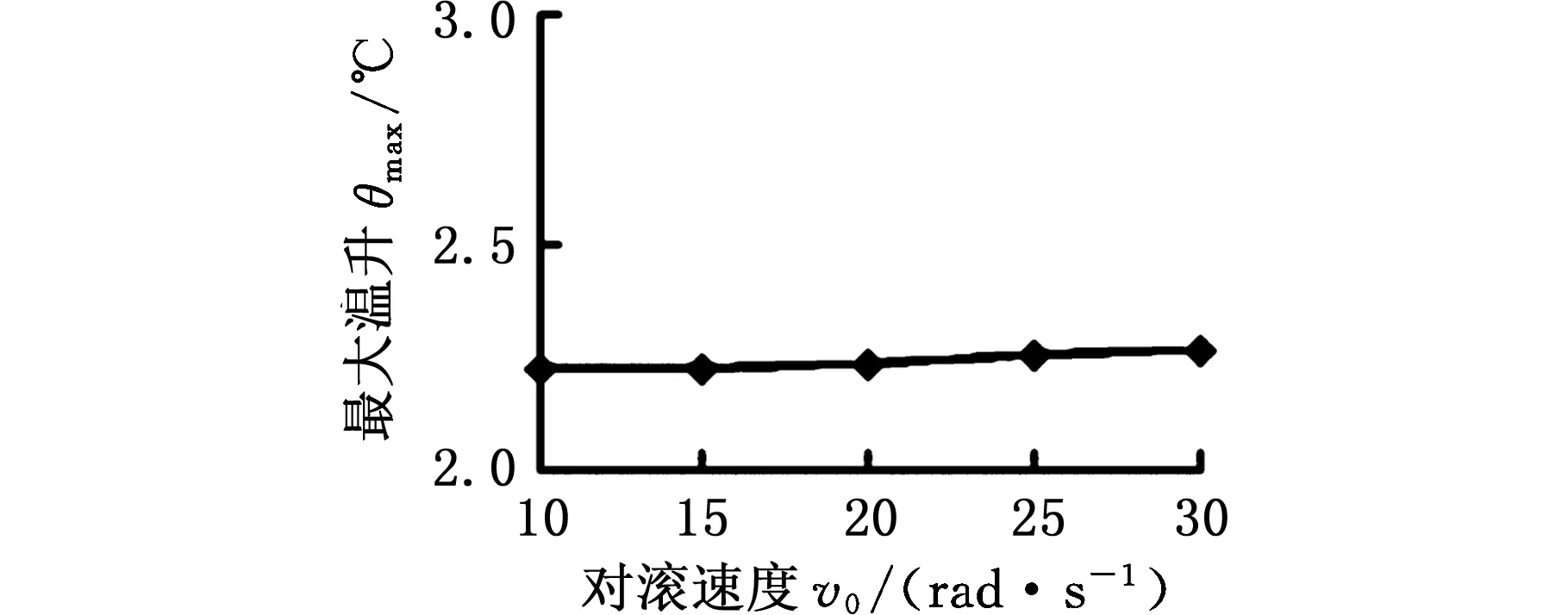
图7 不同速度下的温升Fig.7 Temperature rise under different speeds

由图7可以看出，随着两辊对滚速度的增加，两辊间接触区油墨中间层的温度变化不大，即对滚速度对温升的影响较小。

3.5 材料对接触区温升的影响

由于软辊的材质多为橡胶，且不同橡胶的弹性模量等参数相差较大，为了分析不同材质下的油墨层的最大温升，本节分别选用弹性模量为8 MPa、16 MPa、24 MPa、32 MPa的橡胶进行温度场分析。

保持其他参数不变，只改变橡胶材质，接触区油墨中间层最大温升见图8。可以看出，随着软辊弹性模量的增大，油墨中间层的最大温升提高，由8 MPa时的2.23 ℃升高到32 MPa时的2.94 ℃。这是由于软辊弹性模量的增大导致了当量弹性模量的增大，当量弹性模量的增大导致了接触区压力分布的变化，压力的增大使得油墨层温度提高。

图8 不同软辊材料下的温升Fig.8 Temperature rise under different materials

4 结论

(1)比较沿厚度方向不同位置处的墨层温度变化，结果显示中间层油墨温度最高，越靠近两墨辊处温度越低。这是由于靠近两辊表面的油墨受换热的影响，流失了一部分热量，且热导率低的材料表面温度较高。

(2)随着载荷的增加，油墨中间层最大温升提高。这是由于载荷增加即接触区的压力增大，随着压力的增大,油墨黏度增大，同时能量方程中的耗散功一项增大，进而使接触区最大温升升高。

(3)随着两辊对滚速度的增加，两辊间接触区油墨中间层的温度变化不大，即对滚速度对温升的影响较小。

(4)随着软辊弹性模量的增大，两辊间接触区油墨中间层的温升逐渐提高。