一种直觉模糊重要型多属性消错决策建模方法*
张洋铭,陈云翔,罗广旭,刘 念
(1.解放军63928部队,北京 100020;2.空军勤务学院,江苏 徐州 221000;3.解放军94188部队,西安 710051)
0 引言
消错理论是由广东工业大学郭开仲教授创立,以减少和(或)消除损失为研究目的,以定性和定量相结合为研究方法的一种系统分析方法[1-3],与可拓学、果壳论、集对分析和灰色理论并称为我国五大新兴智能基础学科。消错决策则是从研究错误损失入手,通过判别错误的规则、错误集合、错误函数等,为决策者规避错误、降低错误风险进而作出最优决策提供依据。由于消错决策的理论体系仍处于初步发展阶段,对于很多不确定环境下的决策问题,如直觉模糊多属性决策问题等,并未作出全面的探讨。
而对于直觉模糊多属性决策问题,学者们采用很多方法来解决,如文献[4]利用得分函数法,文献[5]利用简单理想解法,文献[6]利用灰色关联系数法,文献[7-8]利用多准则妥协解排序法,文献[9]利用证据理论等。这些研究实质上默认直觉模糊决策全过程不会出现任何决策错误,这与实际情况并不能完全相符,毕竟决策错误的风险是现实存在的。这也说明直觉模糊决策过程中需要针对决策错误问题进行分析,从错误损失最小角度甄别最优策略或方案。
鉴于此,本文将消错决策理论应用于解决直觉模糊多属性问题中,由于消错理论中将属性分为关键型属性、重要型属性和冗余型属性,为避免特殊属性类型对一般性规律的影响,本文以重要型为属性类型展开研究,探讨直觉模糊集下的错误规则、错误函数、错误损失矩阵等,给出直觉模糊重要型多属性决策的一般步骤,并运用案例进行阐释。
1 消错理论和直觉模糊集的基本知识
定义1设U是论域,u∈U,G是U上的一组确定且有资格的规则,若从G推不出u(包括完全、部分或可能推不出等),称u在U上对于规则G是错误的。
定义2设 U'={u1,u2,…,um}是建立在论域 U 上的一个对象集,G是U上的一组规则,令V={(u,G)|u∈U'},f:V→R,则称f为定义在U'上对于规则G的错误函数,简记为e=f(u),其中R为实数域,e为对象u在规则G的错误值。
定义3以多属性决策问题U为论域,C是用于描述U的属性集,c∈C,a'为属性c的随机错误策略,a+是所有属性均没有发生错误的目标策略,d为a'偏离a+的程度,当d为100%时,则称c为关键型属性;当d=0时,则称c为冗余型属性;当d为[0,100%]时,称c为重要型属性,重要型属性的一个极其重要的特性是可以进行错误补偿。d的最大可能值为属性c的错误极限损失值,表示为d*,称e和d*的积为属性c的错误损失值。通过错误损失值排序可以选取最优策略。
定义4设X为一给定的论域,则X上的一个直觉模糊集定义为:

直觉模糊集的和:

直觉模糊集的数乘:

直觉模糊熵:

定义6直觉模糊集欧几里得距离:

如果不同元素具有不同的权重,则需要使用加权直觉模糊距离。
定义7比较直觉模糊集大小的得分函数[4]和精确函数[10]为:

文献[10]中介绍的直觉模糊集排序规则有:
定义8为研究直觉模糊群决策问题,需要对决策群体的决策信息进行集结,直觉模糊集加权集结算子IFWA:

2 直觉模糊重要型多属性决策模型
根据消错理论的基本知识和直觉模糊集的特性,可以假设直觉模糊重要型多属性决策问题中为属性集,为策略,为属性权重,为决策矩阵,i=1,2,…,m,j=1,2,…,n,表示属性 nj期望达到的完全目标值,表示属性nj的完全错误值,m+表示完全目标策略,m-表示完全错误策略。按照这些假设,可以作出以下定义。
2.1 直觉模糊错误规则
直觉模糊重要型多属性决策问题中,判断策略mi的属性nj错误与否的规则Gj是指属性值是否达到或者超越目标值,其表示为:
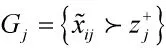
2.2 直觉模糊错误函数
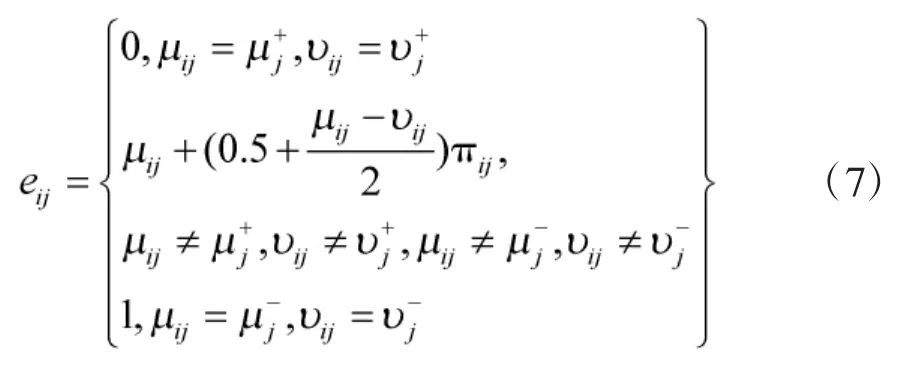
2.3 直觉模糊错误极限损失值
由定义3知道在消错理论中d为错误损失值,是策略偏离目标策略的程度,d*为错误极限损失值。对于直觉模糊集而言,用来表征直觉模糊集偏离程度的量为直觉模糊距离,但是根据文献[13]阐释,利用传统直觉模糊距离公式(如式4)将会得到确定数形式的距离测度,这与直觉模糊集本身反映的犹豫度性质不符,需要构建如下直觉模糊距离测度:


2.4 基于直觉模糊可能度的错误损失排序方法
由定义3可知,在消错理论中将y=e×d*称为错误损失函数,那么模糊错误损失矩阵。通过对Y进行优选计算,可以得到错误损失最少的优选策略。但是对于直觉模糊错误损失矩阵而言,yij仍为直觉模糊集,为避免削弱直觉模糊错误损失矩阵的直觉模糊特性,这里不使用传统的TOPSIS等以设计确定值来进行优选的决策方法,采用基于直觉模糊可能度的排序优选方法[14]。可能度法是通过比较所有策略、综合所有属性两两比较的错误损失可能度信息,令对第k个属就是该决策问题的直觉性,策略i的错误损失大于策略j的可能度为,可能度[14]的计算方法可以采用:

由此形成错误损失可能度矩阵:
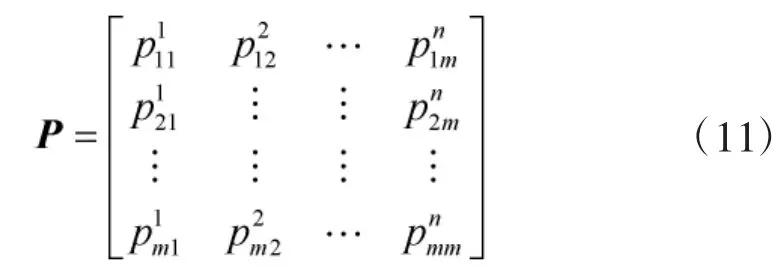
最终比较每一个策略的错误损失可能度排序向量值:

通过比较排序值的大小,排序值越小的说明错误损失越小,策略越优,从而选出最优策略。
2.5 直觉模糊重要型多属性消错决策方法步骤
根据直觉模糊集消错知识系统,就可以明确直觉模糊重要型多属性消错决策步骤为:
步骤1构建直觉模糊错误规则;
步骤2确定直觉模糊错误值;
步骤3计算直觉模糊错误极限损失值;
步骤4建立直觉模糊错误损失矩阵;
步骤5若属性权重未知,则需要根据原决策矩阵的直觉模糊熵求解属性权重,方法较为成熟[15-16],此处不再赘述;
步骤6利用直觉模糊可能度进行错误损失排序和决策。
更进一步地,对于k个决策者的直觉模糊重要型多属性消错群决策而言,对于决策矩阵Dk,为避免由于错误信息集结导致的错误损失情况改变,首先应将Dk转化成错误损失矩阵Yk,再利用集结算子进行集结,得到综合错误损失矩阵Y,再进行上述所列方法步骤即可进行群决策。
3 实例分析
现要针对大型双跑道机场的车辆保障中心进行选址,机场保障部门邀请了3位行业专家通过保障距离N1、停放面积N2和消防措施N33个属性方面综合考量,从A、B、C、D 4个机场保障点选择最优车辆保障中心。假设现在知道专家的决策权重为,属性权重分别为,3位专家的决策信息如下:

根据直觉模糊重要型多属性群决策步骤,首先明确完全目标策略和完全错误策略,构建直觉模糊错误规则G={G1,G2,G3},其中:

不能满足上述错误规则的决策信息都有错误损失,但是由于重要型属性可以互相补偿,所以可以通过综合研究错误损失情况进行消错决策。根据式(7)分别计算D1~D3的错误函数矩阵:
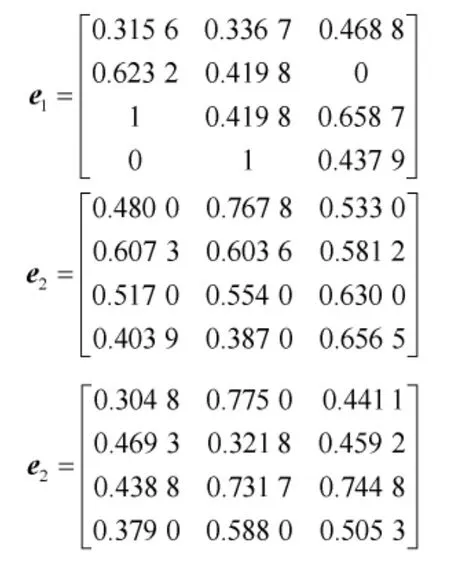
通过观察错误函数矩阵可以直观地看出,关于属性N1,专家1对保障点C的直觉模糊决策信息错误值为1,是完全错误的,而对于保障点D的直觉错误值为0,又是完全正确的,这充分说明在直觉模糊群决策中,决策者的直觉有可能符合实际、决策准确,也有可能脱离实际、决策失误,这在以往直觉模糊决策方法理论中未曾深究,也从侧面反映出通过消除错误角度解决直觉模糊决策问题的必要性。
根据式(9)计算各属性的直觉模糊错误极限损失值:

利用直觉模糊数乘式(2)和y=e×d*求解各位专家的直觉模糊错误损失矩阵:
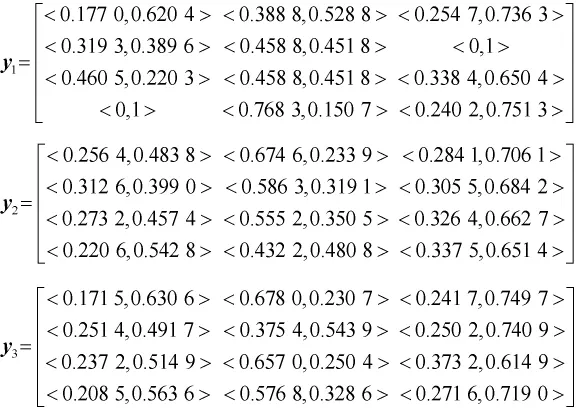
根据式(6)的信息集结规则将专家直觉错误损失矩阵进行集结,可得该决策问题的综合错误损失矩阵:

根据式(10)、式(11)可以得到综合错误损失可能度矩阵:

由式(2)可知4个保障点的综合错误损失可能度排序向量值为:
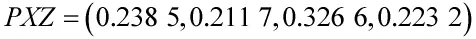
由 PXZ的意义可以知道,A、B、C、D各个保障点综合错误损失可能度最大的是C,最小的是B,也即从消除错误损失角度看应该选择保障点B作为该大型双跑道机场的车辆保障中心。
4 结论
本文从拓展直觉模糊集范畴内的消错理论和消除直觉模糊决策问题中错误的角度,较为深入地研究了直觉模糊多属性消错决策问题。通过剖析消错理论中对错误规则的定义、对错误函数的运用、对错误损失的计算,初步构建了直觉模糊多属性消错知识系统,列举了直觉模糊重要型多属性消错决策的一般步骤及群决策时需要进一步注意的问题,最后通过实例分析证明了直觉模糊消错决策的必要性以及本文方法步骤的适用性,为直觉模糊多属性决策提供了一种新的借鉴思路。当然,本文旨在阐释直觉模糊多属性消错决策的一般规律,对于直觉模糊关键型消错决策和冗余型消错决策并未涉及,将会在后续研究中进一步分析探讨。

