多无人机协同打击任务的攻防博弈策略研究*
陈 侠,李光耀,赵 谅
(沈阳航空航天大学自动化学院,沈阳 110036)
0 引言
博弈论作为一门现代科学体系,源于20世纪初,在二战后发展成为一门完整而丰富的理论科学,将博弈论应用到军事作战中已成为国内外学者研究的热点[1-5]。随着作战环境的日益复杂,无人机作战任务也日益多样化,多机协同作战能够实现攻击多个敌方目标,具有较高的杀伤概率,因而将成为未来空战的主流趋势。多机协同是指两架或两架以上战斗机相互配合、相互协作,执行任务的作战方式[6]。多机作战与一对一作战相比,最显著的差别就是面对多个任务目标需要根据我方资源为各个友机进行目标分配和火力分配。然而,多无人机在执行任务中,能否成功完成任务的关键问题之一是无人机之间的妥善协调问题[7]。如何通过合理的决策策略使得无人机相互协调完成复杂任务是无人机领域研究的热点问题[8]。文献[1]主要利用博弈论构建了导弹攻防技术的数学模型,描述了攻防双方的策略集,利用规划法,求解出了博弈双方的纳什均衡值。文献[2]根据多机协同对抗多目标的空战特征,以敌我双方可能的相互攻击组合方式作为策略集,建立完全信息下博弈模型,确定双方的支付矩阵,给出了纳什均衡值的求解方法。文献[3]针对不确定环境下的军事指挥决策问题,提出了不确定影响因子概念,反映战场不确定环境对各参战单元产生的影响程度,建立了不确定环境下的对抗决策模型[4-5],并通过不确定模拟方法进行求解,结合双矩阵对策方法得到对抗策略平衡点。文献[6]通过分析实际战场中目标价值和毁伤概率信息的不确定性,提出了不确定信息条件下需要解决的无人机(UAV)攻防博弈问题。以敌我双方发射导弹的价值信息为依据,建立基于不确定信息的多UAV攻防对抗的支付函数,构建攻防双方博弈支付矩阵,确定双方的支付矩阵,给出了纳什均衡值的求解方法。但在已有的文献中,建立的多机协同对抗博弈模型没有考虑多无人机协同打击的能力问题,也没有考虑目标需要获得被打击的能力值问题,计算航程代价均考虑始发点与目标点之间的航程,并没有考虑无人机发射导弹的航程,建立的多无人机协同对抗博弈模型还不是很完善。
目前,在多机器人任务分配中,考虑机器人能力函数的研究成果已经引起了有关学者的重视[7-8],文献[7]提出了一种基于效用函数的多机器人系统任务分配策略,在机器人能力向量和子任务要求的能力向量基础上,建立了效用函数的数学模型,根据效用函数大小进行任务分配。文献[8]提出了一种基于机器人效用函数的多机器人系统任务分配新方法等。但迄今为止,关于多无人机协同打击能力的博弈问题尚无文献报道。本文通过建立无人机的能力函数及其雅可比矩阵,给出了多无人机协同打击位置的计算方法,提出了多无人机协同打击的博弈方法,根据敌我双方收集的各个作战参数的信息,建立敌我双方攻防对抗的博弈模型,给出纳什均衡求解方法。
1 无人机能力函数的建立
能力函数是体现无人机对目标的打击能力,主要是根据任务的要求和形式来建立。能力函数与无人机与目标之间的距离和方位等因素有关。多无人机的能力函数是单无人机的能力函数之和。为了简化分析,假设能力函数仅考虑与目标点的距离,当无人机与目标点的距离满足要求时,无人机就能实现最大的能力值[9-12]。
无人机的位置信息存储在n×3矩阵中,n表示无人机的数量。目标点信息存储在m×3矩阵中,m表示目标数量。无人机与目标初始位置矩阵分别为:
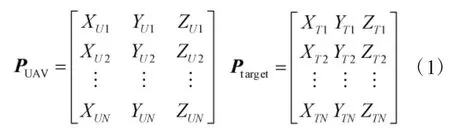
无人机i与目标j的距离dij描述为:

设无人机的作战半径为Di,假定能力函数的最大值为1,目标j获得无人机的能力函数Ci为:

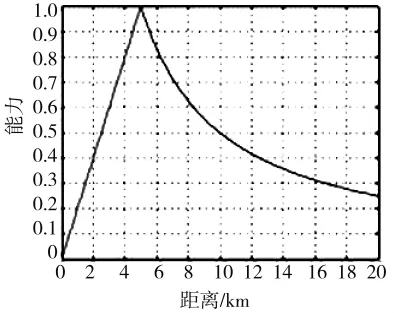
图1 无人机能力函数曲线
假设作战侦察半径为4.5 km,通过图1所示能力函数曲线可以看出:当无人机与目标的距离大于4.5 km时,能力随着距离的增加而下降;当无人机与目标的距离小于4.5 km时,能力随着距离的增加而上升;只有当无人机与目标的距离等于4.5 km时,无人机释放最大的能力。
1.1 雅可比矩阵
对于我方无人机,为了更有效地完成任务,需要分析无人机位置变化对目标所需要的武器能力的影响,建立能力函数的雅可比矩阵,可描述无人机的位置变化对于目标所释放的能力的影响:

目标j获得的能力函数Ci相对于无人机i的位置偏导数为:

1.2 多无人机协同打击位置计算
能力函数由无人机的位置决定,能力函数的变化与位置的关系为:



式中,J+表示伪逆;JT表示雅可比矩阵的转置。
若多无人机协同打击不能达到理想的目标能力值时,需要更新无人机的位置。根据式(9)得到的无人机位置的理想变化值,设时间步长Δt,可以求出无人机新的位置,无人机的位置更新方程为:

1.3 多无人机协同打击航程的计算
通过将无人机更新后的位置坐标带入式(2)、式(3),得到新的无人机能力值,按照式(11)更新无人机位置,直到达到理想能力值,进而得到打击位置各无人机的位置信息,从而得到各种策略我方无人机的航程为:

2 多无人机攻防博弈模型的建立
2.1 矩阵博弈的定义
对于博弈的三要素 {局中人集、局中人的策略集、局中人的支付函数},矩阵博弈需要满足下面的3个条件:
2)局中人1、2分别有各自的策略集,这些策略集是分别由有限的策略组成。
2.2 攻防双方的策略集
无人机攻防博弈分别可以看作参与者1和参与者2,1为我方无人机进攻方,2为敌方防御方。无人机作为进攻方,自身携带杀伤性武器如对地导弹能对敌方造成损失,无人机打击的目的是使自己生存率最大的情况下造成敌方最大的损失;地面防御方是我方无人机打击的目标,地面防御方的目的是减小无人机对自己造成的损失,可以发射干扰弹,干扰我方无人机的通讯系统,降低导弹的命中率进行防御,也可以发射地空导弹,直接对我方无人机进行反击。在敌我双方对抗的过程中,双方都在寻找最优的策略,找到博弈矩阵的纳什均衡点。
3 多无人机协同打击能力的博弈支付函数的建立
3.1 我方无人机打击收益
在多无人机作战过程中,目标价值收益是首先考虑的一个重要指标。我方无人机打击收益需要考虑打击敌方目标的价值,及打击敌方目标所需导弹的价值。假设目标价值集合为,我方无人机导弹价值为为我方打击收益的最大值,即为我方第i架无人机攻击敌方第j个地面目标的打击概率,则收益指标函数为:
若q架无人机合作同时攻击第j个目标,则我方q架无人机攻击敌方第j地面目标的收益指标函数为:
3.2 航程代价指标函数
假设dij为我方第i架无人机初始位置与打击第j个目标位置之间的距离,dmax为我方所有无人机与目标之间的最大距离,即,则我方第i架无人机的航程代价指标函数为:


3.3 敌方目标打击收益

则我方q架无人机合作同时攻击敌方第j地面目标的损伤代价指标函数为:

若q架无人机同时攻击敌方第j个目标时,则敌方r个防空火力对我方第i架无人机的摧毁概率为:

3.4 多无人机协同打击任务的攻防博弈支付函数
综合上述优化模型,可以得到我方第i架无人机打击敌方第j个目标的支付函数为:

其中,w1+w2=1,w1和w2分别为目标价值收益指标权重及航程代价指标权重。

无人机攻防对抗博弈的收益都是一系列的数值,这些数值是博弈双方的支付值,得到敌我双方的支付矩阵:

4 博弈纳什均衡值的求解
4.1 博弈的基本概念
4.2 h人有限策略静态博弈模型与纯策略纳什均衡
设参与有限策略静态博弈的有3个局中人,第i个局中人可采取的纯策略为:
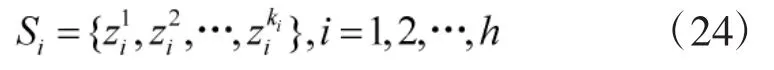
n个局中人的纯策略构成的纯策略空间为:

策略空间S中的任一策略组合为:

记

显然

不失一般性,当1<i 定义2设在h人有限纯策略静态博弈中,第i(i=1,2,…,h)个局中人的效用函数为。 若存在 使 则称 为h人有限策略静态博弈的一个纯策略纳什均衡(Nish Equilibrium)。也称z*是一个纯策略纳什均衡解。 多无人机协同打击任务博弈算法流程图如图2所示。 图2 博弈算法流程图 假设我方无人机4架,分别各自携带导弹1枚,敌方反导防御阵地2个,每个反导阵地有导弹2枚,本文4架无人机执行两个地面目标任务, 无人机和敌方击毁目标的概率信息分别如表1和表2所示。 表1 UCAV对敌方阵地的杀伤概率 表2 敌方阵地对UCAV的杀伤概率 下面分别采用两种方法,给出解决多无人机协同打击任务的攻防博弈策略的方案。 方法1按照以往多无人机攻防博弈方法,没有考虑多无人机协同打击能力函数,也没有考虑目标需要获得的能力值,考虑从起始点到目标的航程代价,得到各个方案收益为: 由纳什均衡可知0.489 2即为所要求的纳什均衡点,即我方采取第7种策略(UCAV1、UCAV4攻击目标 1,UCA2、UCAV3攻击目标 2),敌方采取第1种策略(目标1反击,目标2反击)时,双方收益最大。 方法2通过式(2)~式(4),计算出多无人机的能力函数,雅可比矩阵,根据式(12)~式(22)计算支付矩阵,根据式(23)得各支付值如下所示: 由纳什均衡可知0.505 0即为所要求的纳什均衡点,即我方采取第13种策略(UCAV2、UCAV4攻击目标 1,UCA1、UCAV3攻击目标 2),敌方采取第1种策略(目标1反击,目标2反击)时,双方收益最大。 从两种方案结果可以看出,两种方法的不同之处主要包含以下几方面:一是方法2的决策结果与方法1的决策结果完全不同,即在方法1中,我方的决策结果是策略7,而方法2的决策结果是策略13;二是方法1的收益比方法2的收益小,即方法1的最大收益为0.489 2,而方法2的最大收益为0.505 0。因此,可以得出如下结论:考虑多无人机协同打击能力的博弈(方法2)与没考虑的博弈(方法1)相比,更全面地考虑了影响敌我双方决策的因素,获得了更大的收益值,能更好地评估收益值和打击效能,且提高了多无人机的协同打击能力。 本文针对确定信息环境下的多无人机攻防对抗博弈问题,给出了一种新方法。建立了基于打击位置的多无人机攻防对抗的支付函数,构建了攻防双方博弈支付矩阵。结合统计学和博弈分析方法求出纳什均衡值。并给出了基于打击位置的纯策略的求解方法,验证了方法的可行性及有效性。



5 多无人机协同打击任务博弈流程图
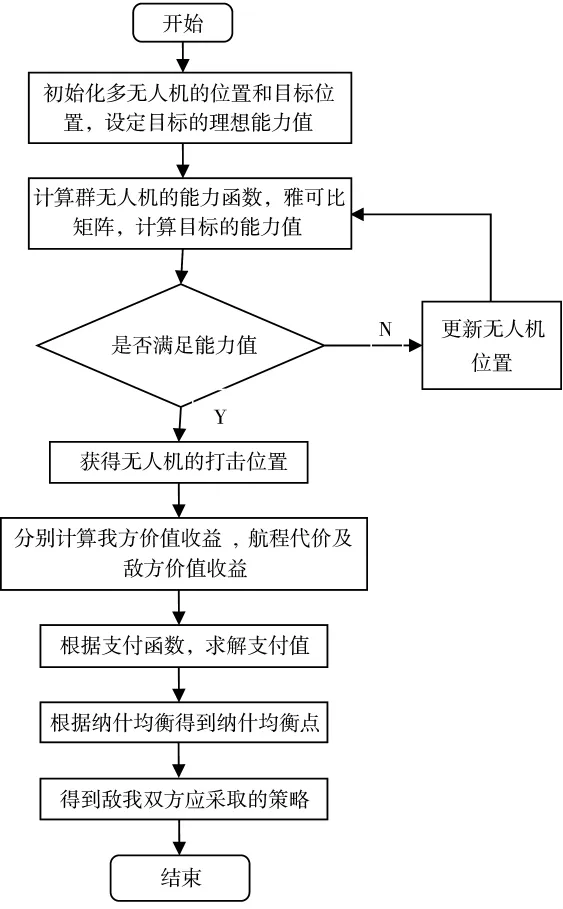
6 仿真研究





7 结论

