分布式在线共轭对偶梯度算法

吕净阁

（安徽理工大学 数学与大数据学院，安徽 淮南232000）

近年来，由于云计算和大数据等新兴领域的到来，所涉及的数据具有数量大、维度高等特点，分布式凸优化理论与应用便得到越来越多的关注，并逐渐应用于传感器网络[1-2]，资源分配[3-4]和机器学习等方面。分布式优化与多智能体系统有着密不可分的关系，分布式计算通常基于多智能体系统中的每个智能体或者节点与其邻居的局部信息交换来最小化如下的全局损失函数：

其中x∈Rd是状态决策变量，f1:Rd→R是仅为节点所知的局部凸损失函数。目前，解决分布式凸优化问题有许多种算法：文献[5-7]中提到的通过计算成本函数的次梯度以及网络通讯来实现优化问题求解的分布式(次)梯度算法以及其变体——随机次梯度投影算法；Duchi等人在文献[8-9]中提到的通过引入对偶变量来实现对原有梯度信息的一种保护机制的分布式对偶平均；文献[10-11]则提到通过引入拉格朗日函数将原问题转成其对偶问题，对拉格朗日函数进行求解，对原始变量更新的同时进行对偶变量的更新的分布式交替方向乘子法以及其变体。

此外，在分布式优化中，时变和有向网络是一个基本假设，因此，本文主要考虑网络拓扑是时变且有向的情形。然而，许多实际应用中的分布式优化，需要在动态环境下运行，所涉及的数据是动态的流数据，各个节点的局部成本函数是随着时间变化的，这样就很难对优化问题进行精确求解。在这种局部成本函数随时间变化的情况下，可以采用在线分布式凸优化算法，其本质上是一种在动态环境下对流数据进行实时处理的一种近似求解方法。衡量一个在线优化算法优劣的标准是Regret界—由节点状态的本地估计产生的累积成本与网络成本函数已知时最佳固定决策所带来的成本之间的误差。Regret界越小，代表在线算法性能越好。文献[12]提出了基于对偶平均算法的分布式在线对偶平均，证明了其收敛速度为O(T)，有效提高了算法的鲁棒性与隐私保护性；文献[13]针对分布式动态环境中数据流的实时处理提出了基于交替方向乘子法的分布式在线算法，其二阶方法具有较快的收敛速度。

文献[14]针对时变无向网络提出了一种通过引入共轭凸函数将原始问题转化为其对偶问题，局部函数强凸时其对偶函数可微且梯度函数利普希茨连续的分布式Fenchel对偶梯度算法，并证明了当本地损失函数是强凸函数时，节点以O(l/k)的速度收敛到对偶最优点，以O(l/k)的速度收敛到原始最优点。本文在此基础上提出一种基于权重平衡的分布式在线共轭对偶梯度算法，将网络拓展到时变有向强连通网络，并添加在线设置对动态流数据进行实时处理，分别给出对偶与原始变量Regret界，并证明当本地损失函数是强凸函数且步长时，对偶变量Regret界的收敛速度是O(ln(T+1))，原始变量Regret界的收敛速度是。

1 问题描述

1.1 图论

考虑一个由n个节点构成的有向强连通网络，可以用有向图Gt(V,Et)表示，其中V=(1,2,…,n)代表通信网络中的节点集合，Et⊂V×V代表在第t时刻的有向边集。如果在第t时刻存在一条有向边连接节点i和节点j，则(i,j)∈Et；代表节点i在第t时刻的入度邻居；代表节点i在第t时刻的出度邻居。定义代表节点i在第t时刻的入度和出度。

次梯度：∂f(x)是函数f在点x处的次梯度，如果满足对任意的y∈domf有

由于有向时变网络拓扑会带来不对称性，所以定义如下权重来使网络平衡：

定义[15]节点i∈V的权重wi如果满足

则网络拓扑图Gt是平衡的。

1.2 分布式在线凸优化

在分布式在线凸优化模型中，t∈{0,1,…,T},T∈Z++表示迭代时间的轮次即有限时刻，节点i∈V在第t次迭代从凸紧集K∈Rd中选择一个本地估计xi(t)∈K，继而确定其本地凸损失函数，则t时刻网络成本函数可定义为：

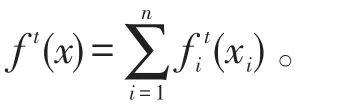
本文考虑以下分布式凸优化问题：

在线优化算法的目的是尽量减小随时间推移由节点状态的本地估计产生的累积成本与网络成本函数已知时最佳固定决策所带来的成本之间的误差，证明其Regret界是关于时间次线性的，即

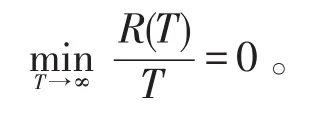
假设1每个节点的局部成本函数是1-强凸的，即∀x,yϵK和在x处的次梯度，有。

假设2时变有向网络拓扑图是强连通图，即在任意时刻t，对所有的节点i,j∈V,都存在一条有向路径。

2 在线分布式共轭对偶梯度

由文献[14]定义凸函数的共轭函数为，则将(1)转化为其对偶问题：

其中CϵRd是集合KϵRd的正交补且是闭凸集，由的强凸性和共轭函数定义知可微且。记gi(t)代表共轭函数在点yi(t)处的梯度，且gi(t)利普希茨连续[14]，则在闭集C上有界，即存在常数L使得。为解决时变有向网络中的分布式在线优化问题，本文在Fenchel共轭对偶梯度算法的基础上添加在线设置提出一个基于权重平衡的分布式在线共轭对偶梯度算法：令xi(t)ϵK为节点i在t时刻的最优点的本地估计，yi(t)ϵC为节点i在t时刻的对偶变量，在每个时刻t∈{1,…,T}，每个节点i∈{1,…,n}进行以下更新：

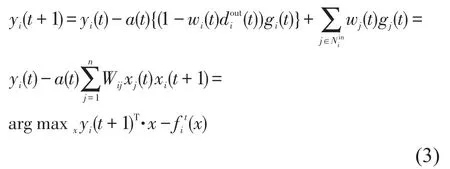
用矩阵的形式表示为：

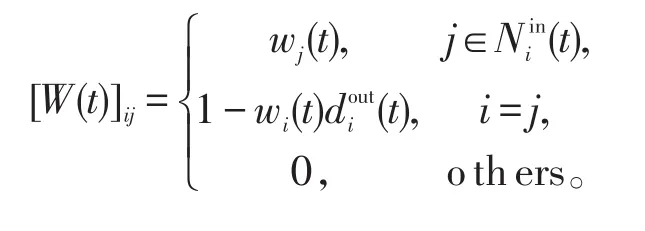
3 DO-CDG算法的收敛性分析

令x*,y*为分布式在线算法的原始最优点与对偶变量最优点，下面给出算法的几个重要结论。为了方便分析算法的收敛性，定义

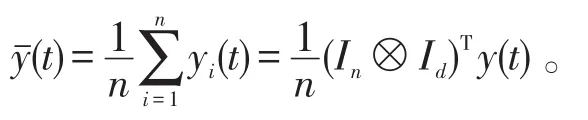
假设3如果假设2成立，权重矩阵W(t),t≥1是列随机矩阵，且元素满足：

其中，C＞0是常数和0＜λ＜1。

由W(t)是列随机矩阵，对等式(4)两边同时乘以得到[16]：

令ri(t)=-a(t)gi(t)，由归纳法得：

同理，由(3)得对偶变量的归纳更新是：

引理1如果假设1、2成立，yi(t)是算法1产生的对偶序列，则对最优点y*∈Rd，有

故(7)的最后一项

由不等式性质得

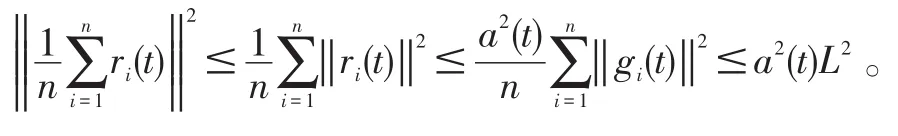
结合上述几个不等式，(7)最终化成

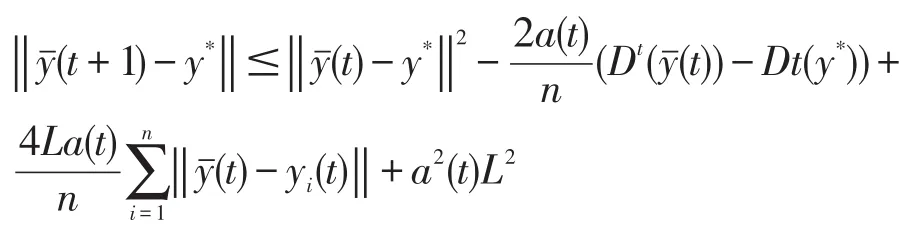
得证。

引理2如果假设1、2成立，yi(t)是算法1产生的对偶序列，则对最优点y*∈Rd，有

证明将引理1从t=1到T累加，并同时乘以得到：

由共轭函数的性质得：

由对偶变量的Regret界的定义知

结合(8)和(9)得出引理2。

定理 1如果假设 1、2、3成立，yi(t)是（3）产生的对偶序列，则对最优点y*∈Rd，有

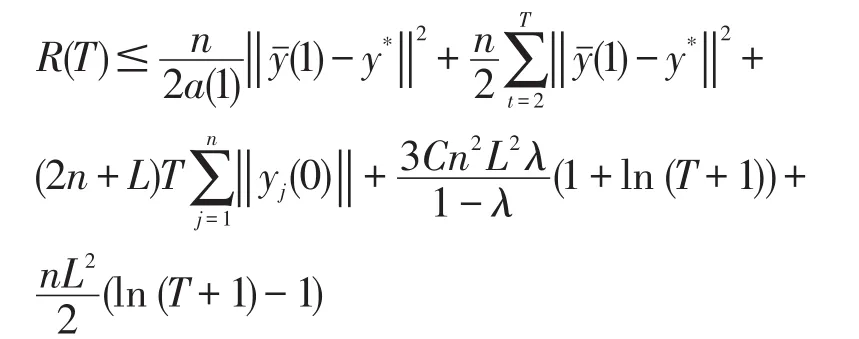
其中，

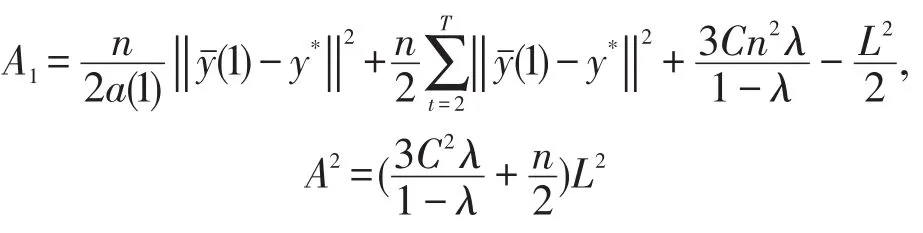
证明由(5)和(6)，得

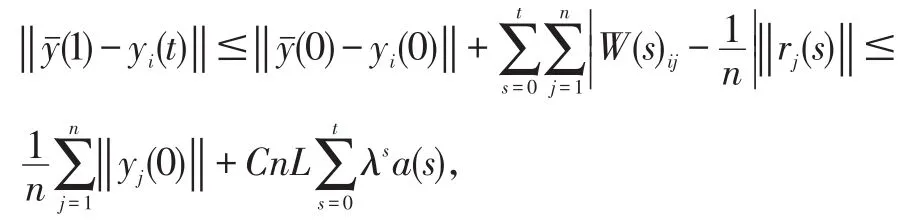
由0＜λ＜1知。由，则

其中

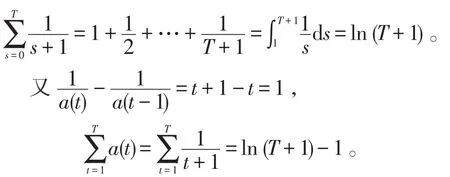
定理 2如果假设 1、2、3成立，xi(t)是（3）生成的原始迭代序列，当取步长为，则有

其中

证明由共轭函数的定义以及算法1知gi(t)=xi(t)，且由假设1知问题(1)和问题(2)是强对偶的，即原问题的最优解f(x*)等于对偶问题的最优解。由凸(凹)函数的性质以及问题之间的转化方式得：

故

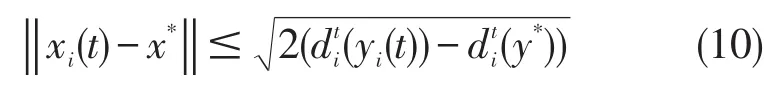
由Regret界的定义得到

得证。

由定理1得对偶变量的Regret界是关于时间T是次线性的，因为

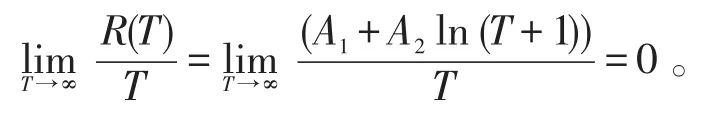
由定理2得原始变量变量的Regret界是关于时间T是次线性的，因为

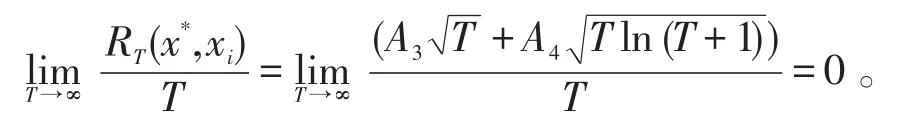
4 仿真

通过使用Matlab软件，考虑n=3即网络包含3个节点，有限时间选择T=100，迭代步长为：这里的每个节点在第t时刻的损失函数设置为：

做出RT/T关于时间t的变化图，如图1所示。可以看出，时间内的平均遗憾随时间的推移是逐渐缩小的，验证了以上的理论分析结果。

5 小结

本文在时变有向强连通网络拓扑下研究了分布式在线共轭对偶梯度算法，将原始问题转化为其对偶问题，通过给出对偶变量的Regret界，还原出原始变量的Regret界，理论分析说明当本地损失函数为强凸函数时，算法1关于对偶变量的Regret界地收敛速度为O(ln(T+1))；关于原始变量的Regret界地收敛速度为，实验证明了算法的有效性。

图1 有限时间内的平均遗憾随时间的变化趋势图