Boussinesq方程的精确孤子解研究

史曙光，刘东生

（南京理工大学 理学院，江苏 南京 201712）

非线性现象在许多科学和工程领域中都广泛存在，例如等离子体物理、固体物理、流体动力学和化学动力学等[1-2]，非线性Boussinesq方程在海洋研究中占有重要地位。经典的Boussinesq方程描述了长波在浅水中的传播[3]。此外，Boussinesq方程还模拟了导致冷锋和急流的大尺度大气和海洋气流[4]。表面重力波的Boussinesq方程已被证明是模拟海岸和海洋地区波浪传播的有效工具。后来，发展了许多新的Boussinesq型方程来扩大方程的适用范围。Wzawaz[5-6]介绍各种类Boussinesq方程模型在湖泊和海洋沙滩的浅水波的研究。近几十年来，波浪在水面上传播的研究取得了重要的理论和实际意义[7-10]。

寻找非线性方程组的精确解有助于理解复杂的非线性物理现象和由这些非线性发展方程模拟的动力学过程。在过去的几年中，人们提出了许多新的方法来寻找孤立的解[11-17]，文献[18-19]采用了直接积分法求解Boussinesq方程的精确解、文献[20]中采用了试探方程法得到了Boussinesq方程的3类精确解，即双曲正切解、正切解和指数形式解，但上述两种方法在求解方程中过程繁琐，且难以克服高阶方程问题，故此文采用新的方法：函数变量法，把偏微分方程转化为常微分方程，然后求解，克服了以往求解繁琐的问题。函数变量法在2010首次提出，随后在很多文献中获得了广泛的运用，文献[21]给出三种不同形式的Boussinesq方程：

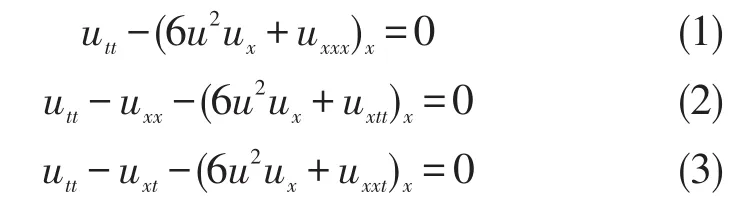
通过两种不同的方法得到一些孤子解和奇异孤子解。

研究目的是用函数变量法求上述Boussinesq方程（1）～（3）的时间分数阶解的精确解。

1 Jumarie的改性Riemann Liouville导数和函数变量的方法

在过去的几十年里，为了提高分数类型的局部行为，Jumarie[22]提出了改性衍生物。Jumarie的导数阶α定义为：

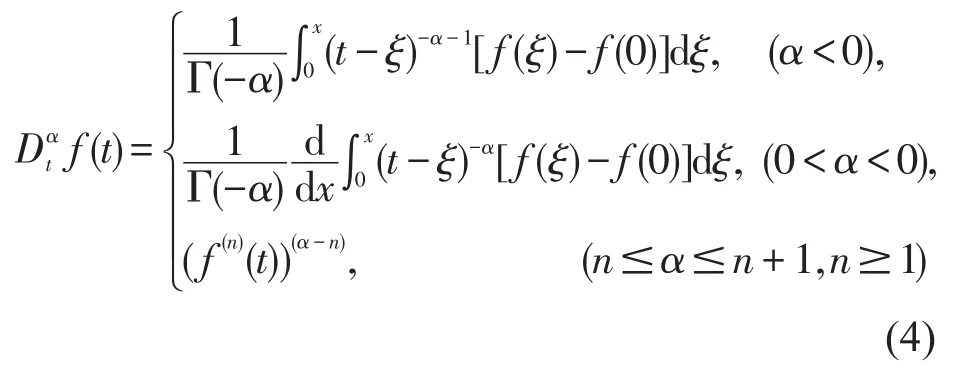
其中：f:R→R,t→f(t)连续，但不一定可微，更多的求解细节在文献[23-24]。根据LU等的观点[24]，在此概述一下使用函数变量法的主要步骤：

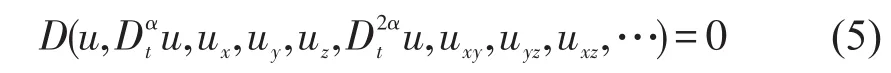
其中：下标表示偏导数，（5）可以转换成ODE。

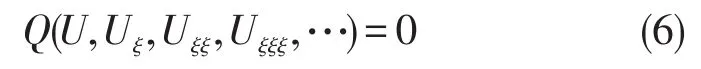
利用变量变换得：

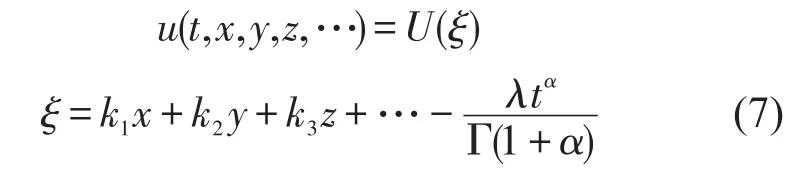
为简单起见，积分常数（s）可以设置为零。

和一些连续导数U：

把（10）带入到（6），用U，F和它的导数来表示ODE：

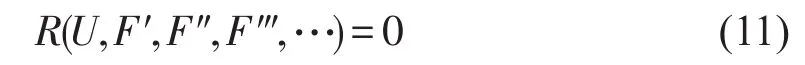
2 第一次分数阶Boussinesq方程

第一类分数阶Boussinesq方程如下：

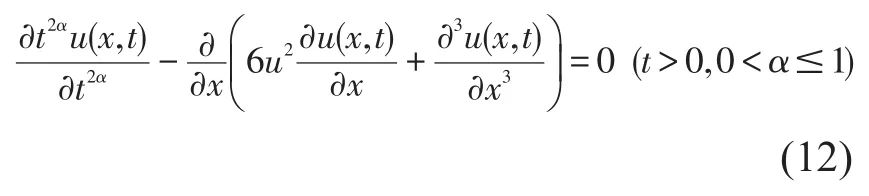
通过变量替换：

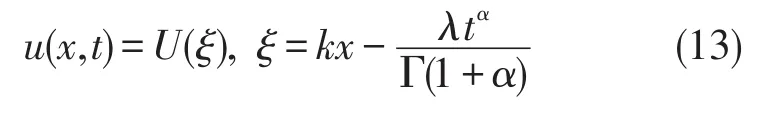
可以把（12）变换成 ODE。

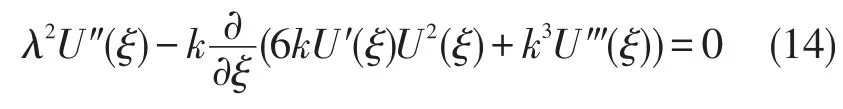
对（14）积分两次，令积分常数为0，得：

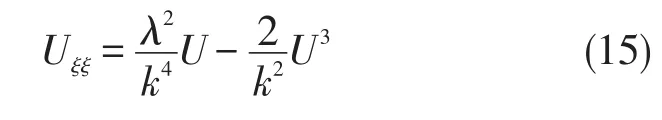
利用变换

把（10）代入到（15）中得：

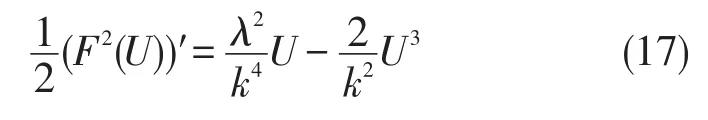
或者

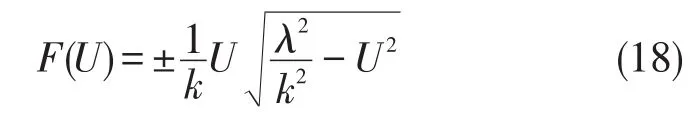
上式的解可以由下式积分直接推导出

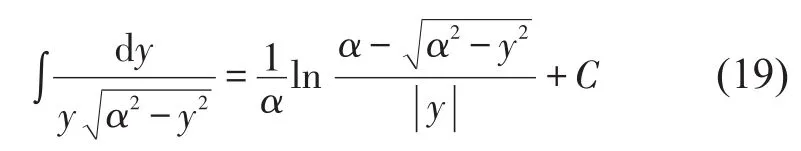
把积分常数置为0，可以解得

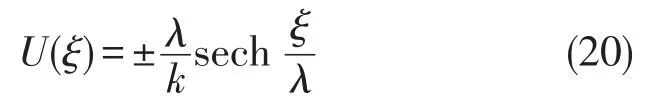
利用变换（13），得到了第一次分数阶Boussinesq方程的如下双曲解：

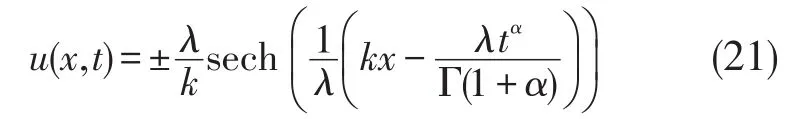
根据图中不同的α，绘制了第一次分数阶Boussinesq方程的解的图形，如图1所示。

图1分别代表λ=2，α=0.05,0.5,1下的解，由图可以看出，孤子波解的波长随α的增加而减小，孤子波的振幅随α的增加而减小，且随着α的增加，孤子波越来越趋于稳定。

3 第二次分数阶Boussinesq方程

第二类分数阶Boussinesq方程如下：

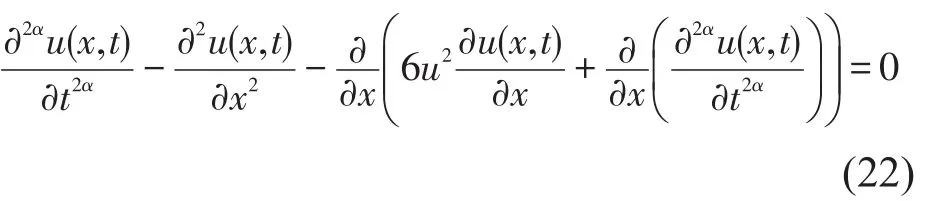
利用(13)进行变量替换，把（22）表示为一个ODE：

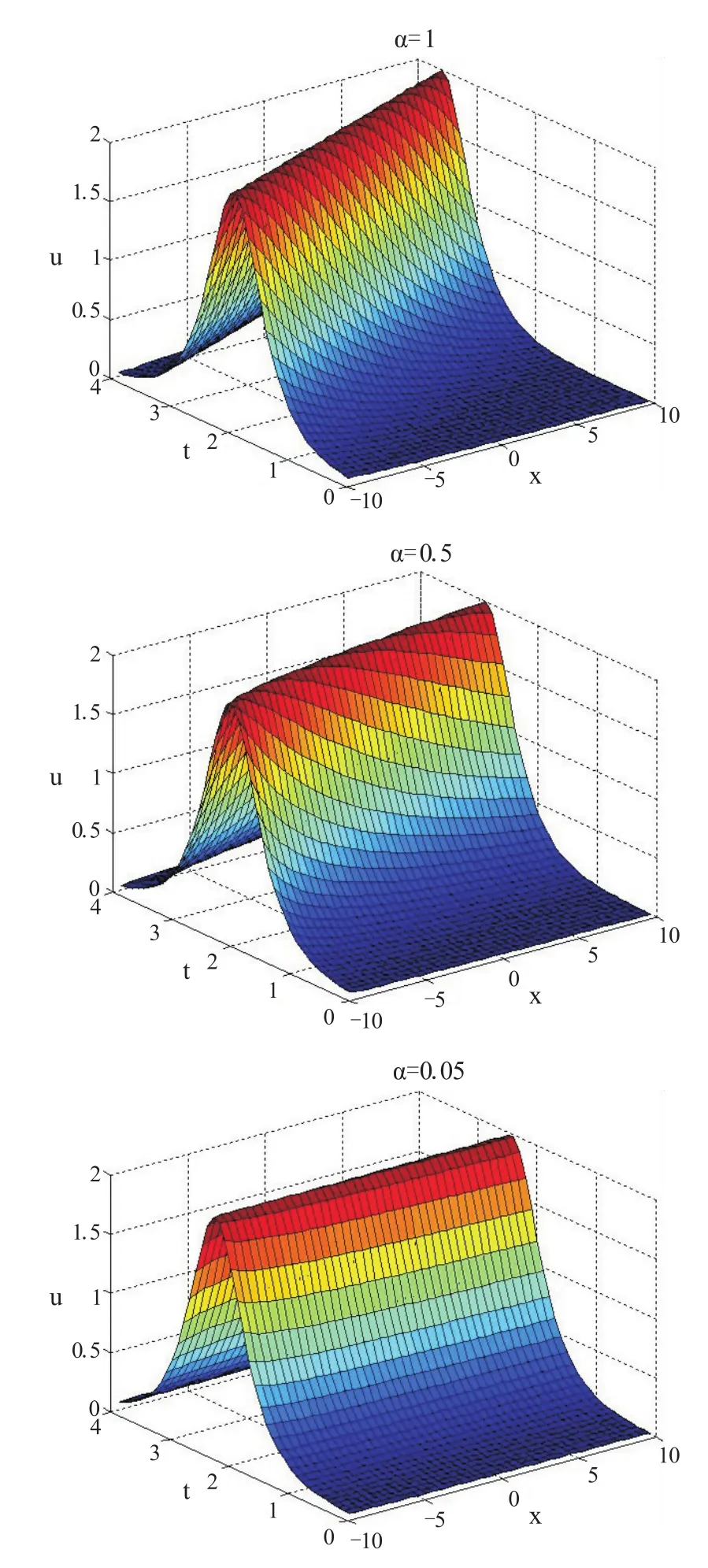
图1 第一次分数阶Boussinesq方程解

因此，利用函数变量法得到了二次分数阶Boussinesq方程的如下双曲解：

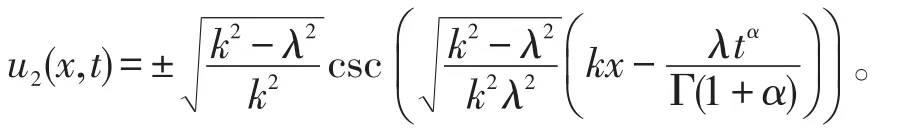
k={x|x≥2⋃x≤-2},λ=2,α=0.05,0.5,1 时u2(x,t)的图像如图2。可以看出（22）的双曲解则没有规律性的特征，但当α=0.5时，方程的解具有轻微周期性，且随着时间的增加，振幅不断减少。

4 第三次分数阶Boussinesq方程

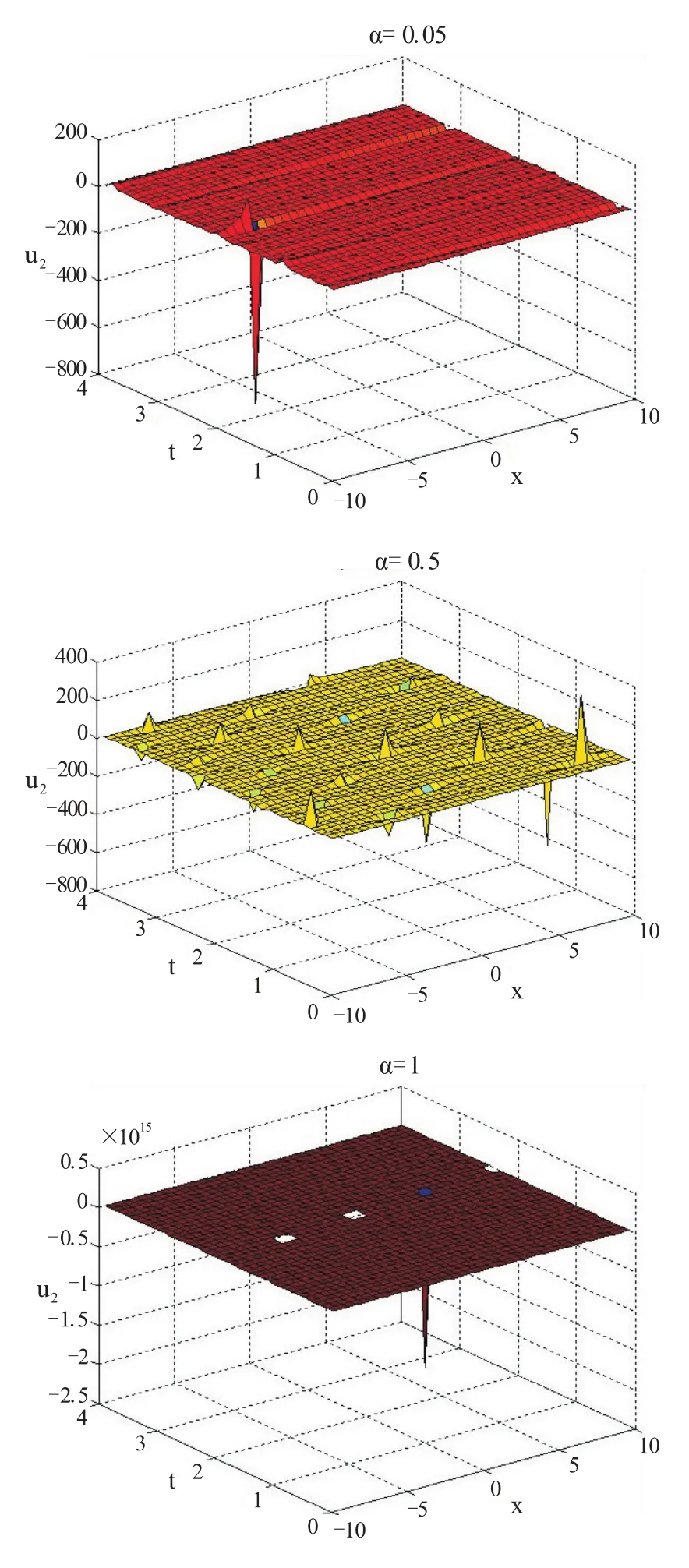
图2 第二次分数阶Boussinesq方程解

第三类分数阶Boussinesq方程如下：

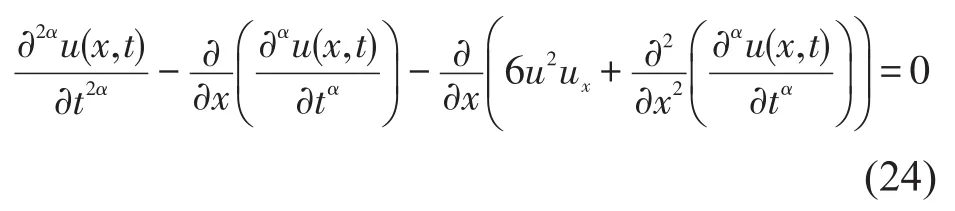
利用(13)进行变量替换，把（24）表示为一个ODE

同样的方法，利用函数变量法得到了三次分数阶Boussinesq方程的如下双曲解：

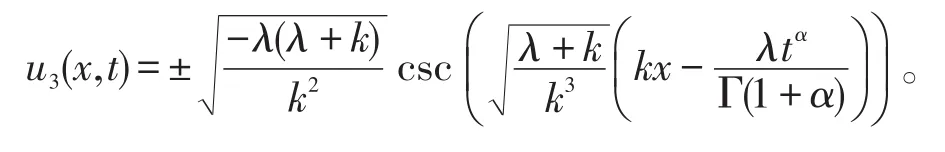
由图3知，当α=1时，孤子波具有明显的周期性，且随着时间的递增，振幅不断降低，当α＜1时，在短时间内孤子波没有明显的周期性质。

5 小结

本文利用函数变量方法成功地得到了分数阶Boussinesq方程的精确孤子解，这些解可以描述周期波和孤立波。该方法简单有效，可以推广到求解非线性时间分数阶或空间分数阶方程组的许多系统。

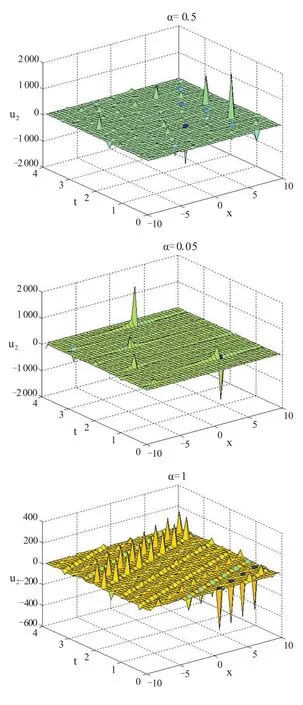
图3 第三次分数阶Boussinesq方程解