高功率微波输出窗内侧击穿动力学的PIC/MCC模拟研究∗
左春彦 高飞 戴忠玲 王友年
(大连理工大学物理学院,三束材料改性教育部重点实验室,大连 116024)
(2018年6月27日收到;2018年9月28日收到修改稿)
1 引 言
随着高功率微波(highpowermicrowave,HPM)器件输出功率提高及脉宽增加,介质输出窗的放电击穿已成为HPM产生与传输的重要限制因素[1−3].放电击穿是一系列复杂物理过程共同作用的结果,它是由二次电子触发,并与介质窗表面释放出的气体发生非弹性碰撞,最终导致放电击穿.国内外学者对于介质二次电子倍增现象已经开展了许多相关的理论和实验研究.在国际上,Neuber等[4,5]进行了HPM窗口击穿实验,利用光学诊断给出了介质沿面闪络与放电击穿的物理图像;Kishek等[6,7]发展了蒙特卡罗方法预估二次电子倍增的敏感区间;Kim和Verboncoeur[8,9]利用一维PIC/MC(particle in cell/Monte Carlo)程序,研究了介质二次电子倍增和表面气体碰撞电离过程;Nam和Verboncoeur[10]利用模拟结果修正电子能量分布函数来完善整体模型.
在国内,常超等[11−15]研究了介质窗周期性矩形和三角形表面轮廓对倍增的抑制机制、解吸附气体和磁场对窗口倍增的影响以及微波脉冲尾部对窗口破裂的增强;郝西伟等[16]分析了二次电子的运动轨迹,给出了电子运动状态随电子发射参数和微波场参数的变化规律,并分析了介质窗表面及内部的导电树枝通道的发展过程;蔡利兵等[17−20]通过一维PIC/MC模拟研究了外加磁场或强直流场时次级电子倍增和气体电离等过程,同时给出了表面释气速率对气体击穿的影响规律;Cheng和Liu[21]利用传输线模型,研究了微波磁场和斜入射微波对电子倍增的影响;董烨等[22−28]利用PIC/MC模拟给出了二次电子倍增的物理过程及特性物理量的变化,研究了释气强度及释气分子的运动速率对介质沿面闪络击穿的影响,并利用PIC/MC与三维电磁流体耦合模型模拟了电磁场对介质窗表面闪络击穿过程的影响.
然而,迄今人们对介质窗倍增放电达到饱和并向气体电离转换过程的研究尚不完善,尤其是低气压条件下,关于微波频率和微波振幅对介质窗击穿时气体电离出现的时间和位置的影响还需要进一步深入地研究.因此,本文采用自主研发的1D3V PIC/MC程序,详细研究了真空及不同气压条件下介质表面击穿过程中的二次电子倍增形成机制以及电子与背景气体碰撞电离的转换过程,并给出了电子密度、离子密度、电场的空间分布,重点考察了低气压条件下微波频率和微波振幅对气体电离出现的时间和位置的影响.
2 物理模型
图1为介质沿面闪络击穿的示意图,其中假定:微波沿−x方向传输,入射电场平行于介质表面沿y方向,Ew=Erf0sin(ωt+ θ),其中Erf0为微波场的幅值矢量,ω=2πf为微波的角频率,f为微波频率,θ是0时刻微波的初始相位.在局部电场增强诱发场致发射或X射线、紫外线在介质表面引发光电发射,初始种子电子由介质表面出射,并在介质表面束缚电荷场(由电子发射后正电荷积累形成)作用下,从微波电场Ew中获得能量后加速撞击介质表面,激发二次电子,如此往复从而出现二次电子倍增效应.电子从微波场中加速获得能量后,与介质表面附近的气体分子发生碰撞电离,形成新生电子和正离子并形成等离子体.
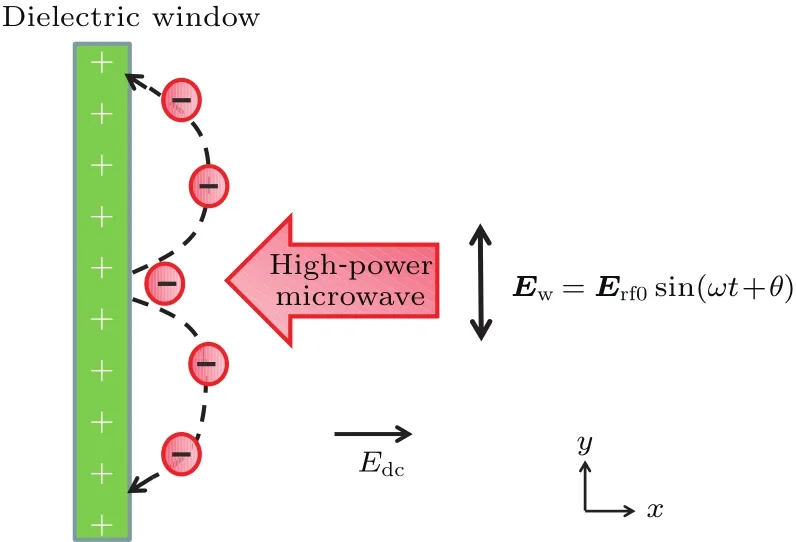
图1 高功率微波介质沿面闪络击穿的示意图Fig.1.Schematic of the multipactor on dielectric surface under HPM.
2.1 PIC/MC模型
本文采用PIC/MC模拟的一维空间分布、三维速度分布(1D3V)模型,对介质表面击穿过程进行模拟.初始化时,将一维空间划分为许多均匀的网格,将带电粒子随机地分布在这些空间格点上,同时粒子速度为三维且服从麦克斯韦分布.带电粒子的运动规律由方程(1)和(2)确定:

其中m和q是带电粒子的质量和电荷;dr是dt时间内粒子的位移,v是该时刻粒子的速度,ϕ是空间电势,ρ是电荷密度,ε0是真空介电常数.在给定初始条件下,采用显示蛙跳格式数值求解运动方程(1)和(2),可以得到不同时刻x方向上粒子的运动信息,并由此统计出不同时刻带电粒子的电荷密度分布∑.然后,对泊松方程(3)进行数值离散,并采用追赶法进行求解,可以得到不同时刻电势ϕ的空间分布,进而通过中心差分得到静电场Edc.当电子与气体分子碰撞时,则采用MC方法来确定带电子与中性粒子的碰撞细节,包括电子弹性碰撞后的散射方向和非弹性碰撞的能量损失等.在模型中具体考虑的碰撞类型有电子与中性原子的弹性、激发和电离碰撞,离子与中性粒子的弹性碰撞和电荷交换碰撞等.当粒子运动到介质窗边界时,应用次级电子发射模型来判断二次电子产额;当粒子运动至右侧自由空间边界时,利用吸收粒子边界条件来模拟粒子逃逸情况.
2.2 次级电子发射模型
本文采用Vaughan提出的经验公式来描述次级电子产生率与初级电子的能量ε及入射角度α之间的关系[29]:
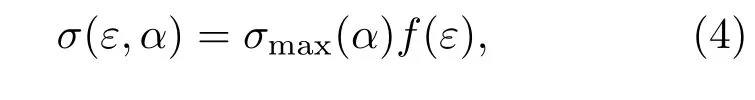
式中

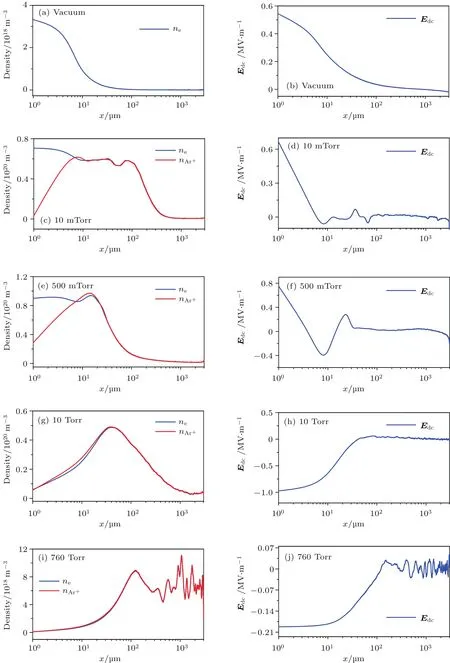
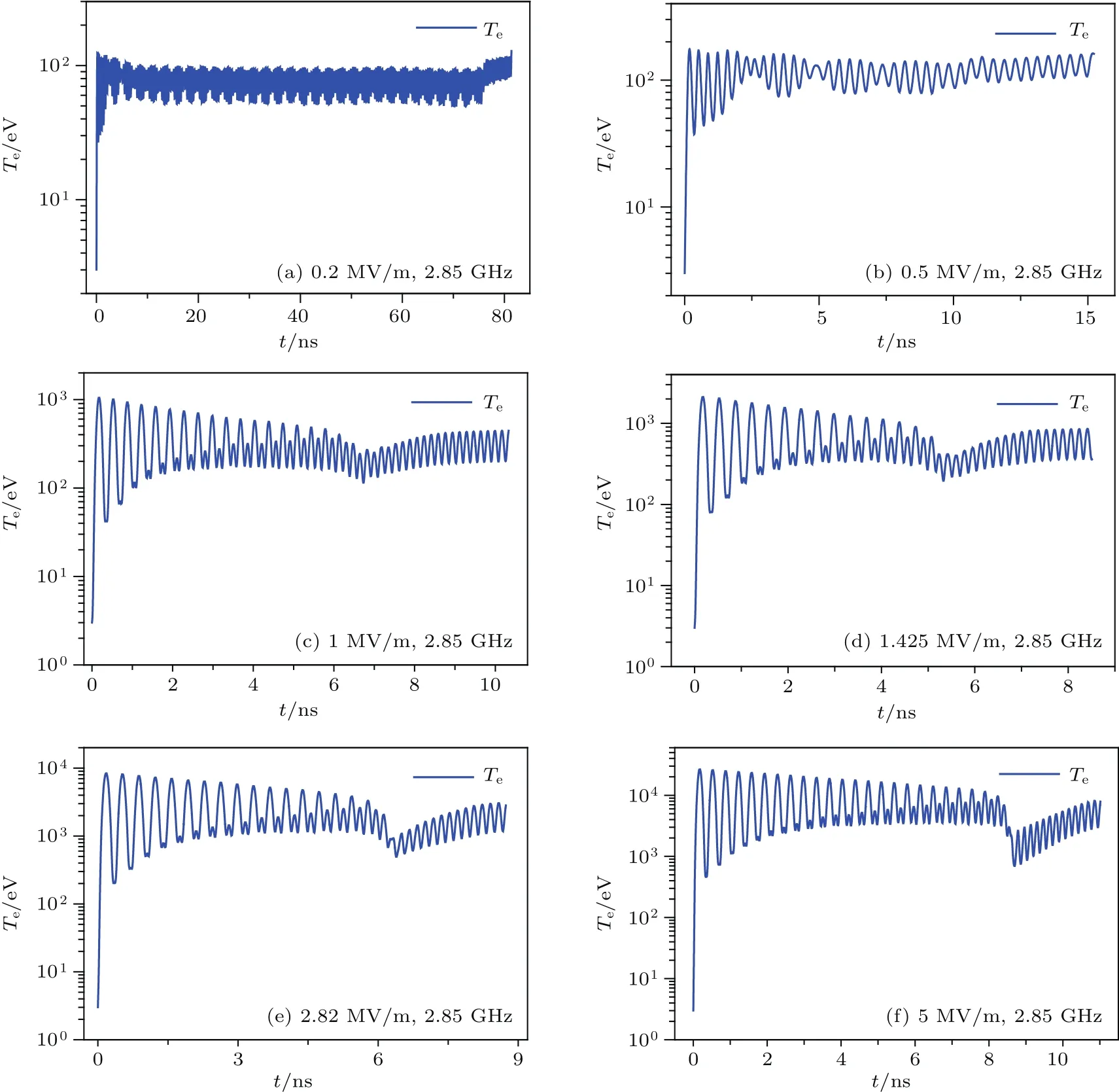
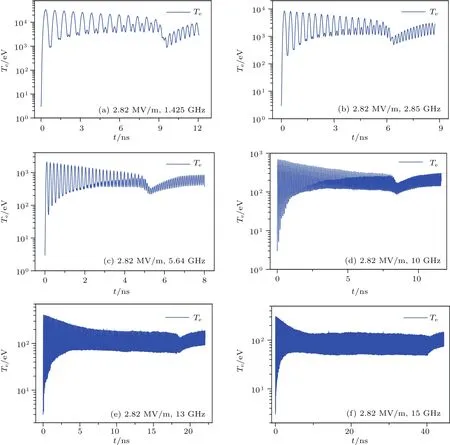
其中σ为次级电子发射率;σmax为正入射次级电子最大发射率,Emax为其对应的入射能量;σmax(α)为斜入射次级电子最大发射率,Emax(α)为其对应的入射能量;α为入射角(α=0代表正入射,α=π/2代表掠入射);ks为表面光滑系数(ks=0,1,2分别代表粗糙、不光滑和光滑);Ei为电子的碰撞能量,Eth为阈值.当Ei 次级电子初始能量概率密度函数满足[6]: 次级电子发射角发射角φ是偏离平行介质表面方向的角度,概率密度函数g(φ)=0.5sinφ,0<φ<π;E0m是次级电子能量分布函数峰值处对应的能量,通常取2—10 eV,本文取为2 eV. 采用上述模型和模拟方法,可以对真空及不同气压下介质表面放电击穿过程中二次电子倍增的形成机制、电子与背景气体碰撞电离的多物理转换过程开展系统的研究.选取参数如下:模拟区域为介质窗内侧3 mm,微波电场幅值0.2—5 MV/m,微波频率1.425—15 GHz,气压0—760 Torr,初始种子电子密度2.45×1014m−3.本文选取介质材料为聚四氟乙烯,其次级电子倍增材料特性参数为:Emax0=400 eV,σmax0=2.12,ks=1. 由于没有考虑材料表面气体退吸附过程,我们假定模拟区域有无限的背景气体.模拟中选用Ar为背景气体,其碰撞截面数据从国际原子能机构网站数据库获得[30].因为介质表面电子运动的平均自由程远小于微波的波长,所以不考虑微波场在传播方向上的分布,模拟中设定微波场仅随时间变化. 图2显示的是介质材料聚四氟乙烯的二次电子发射产额δ随入射电子能量ε及入射角度α的变化关系.随着电子入射能量的增加,二次电子产额先增加后下降[3,31],随着电子入射角度的增加(0—90◦)二次电子产额增加,尤其是在高能区域该现象更为明显.另外,产额曲线与δ=1的直线有两个交叉点εp1(约55 eV)和εp2(约4600 eV),表示入射电子能量在两个交叉点之间时,介质的二次电子发射产额大于1. 图3和图4中的计算结果在数值计算时,选取微波频率为2.85 GHz,微波幅值Erf0为2.82 MV/m.图3给出了真空、10 mTorr,500 mTorr,10 Torr,760 Torr五种条件下电子(e)和氩离子(Ar+)的数量、电子的平均能量Te随微波作用时间的演化规律.在真空条件下,由于仅存在介质窗上二次电子的倍增效应,故不存在气体电离产生的Ar+,如图3(a)所示.在放电初期,电子轰击介质窗,然后介质窗发射二次电子,同时二次电子发射量大于入射电子量.由此导致介质窗上积累正电荷,其产生沿介质窗法线方向的静电电场Edc,并加速电子轰击介质窗,产生出更多的二次电子.介质窗累积的正电荷将产生更强的直流电场,如此重复,直至介质窗处电子平均能量不断降低到二次发射阈值为1的临界能量,这时达到倍增饱和,同时微波周期平均的电子数量和电子能量不再变化,如图3(a)和图3(b)所示.电子倍增饱和后,电子数量和平均能量均以2倍于微波的频率振荡. 图3 在(a),(b)真空,(c),(d)10 mTorr,(e),(f)500 mTorr,(g),(h)10 Torr,(i),(j)760 Torr条件下电子及Ar+数量、电子平均能量的时间演化规律Fig.3.Temporal evolutions of the number of electrons and Ar+,and of the corresponding statistic electron energy at(a),(b)the vacuum,(c),(d)10 mTorr,(e),(f)500 mTorr,(g,h)10 Torr,and(i),(j)760 Torr. 在极低压(10 mTorr)时,粒子数目的时间演化呈现两个阶段,如图3(c)所示,即二次电子倍增阶段(6 6.10 ns),电子数目随时间呈现指数增长;当二次电子达到饱和(>6.10 ns),出现气体碰撞电离的过程,此后电子数目以2倍微波频率振荡的同时以指数增长速度增加,而离子数目仅以指数增长速度增加.值得注意的是,10 mTorr条件下在6.10 ns发生气体击穿,相比于其他气压的击穿时刻(如500 mTorr时6.22 ns,10 Torr时6.82 ns)稍早,是因为气压较低,粒子的碰撞自由程较大,电子在微波场中加速时间更长,获得能量较大,且放电初期快速产生二次电子后,介质窗遗留的正电荷约束电子的运动时间,使其平均能量逼近二次电子倍增区间,如图3(d),并快速达到倍增饱和,发生气体击穿.然而击穿发生后粒子密度的增长较缓慢且平均电子能量有缓慢抬升,这说明此时二次电子倍增效应和气体碰撞电离过程是耦合在一起的,且两者相互促进,但由于此时气压较低电离强度比较弱,粒子增长较慢.电子平均能量的逐渐升高是因为出现气体电离后,Ar+数目增多,由于离子质量远大于电子质量,所以Ar+几乎不响应微波场的振荡,因此电子移位后,遗留的正离子会增加静电电场的振荡幅值,从而导致电子平均能量在气体电离之后逐渐增加. 在低气压(500 mTorr)时,与10 mTorr类似,粒子数目的时间演化呈现两个阶段,如图3(e)所示,即二次电子倍增阶段(6 6.22 ns)和二次电子倍增与体电离共存阶段(>6.22 ns).与10 mTorr不同的是,气压的升高使得气体电离强度增大,粒子密度在气体击穿后快速升高,电子平均能量的升高速度也增加. 在高气压(10 Torr)时,如图3(g)和图3(h)所示,与低气压类似,也包含二次电子倍增阶段(6 6.82 ns)和二次电子倍增与体电离共存阶段(>6.82 ns).不同的是,气压大幅升高使得气体电离强度大幅度增加,气体击穿后的瞬间气体大量电离,粒子密度迅速升高,电子平均能量则急剧减小. 在极高压(760 Torr)条件下,电子及Ar+随着时间的增加呈现指数增长,并且电子数目略低于Ar+的数目,如图3(i)所示.此时,等离子体放电击穿过程由气体碰撞电离主导放电,无明显的二次电子倍增.图3(j)给出的是电子平均能量随时间的演化规律.在放电初期,电子平均能量迅速增加到6.5 eV左右,然后以微波频率的2倍频率做小幅振荡.这是因为高气压下,电子自由程较短,电子与中性气体频繁碰撞,从而导致电子平均能量较低. 图4给出了真空,10 mTorr,500 mTorr,10 Torr和760 Torr五种条件下的介质表面击穿放电稳态后微波周期平均的电子密度、Ar+密度及静电场的空间分布.结果显示:在真空条件下,电子密度随着距离的增加先缓慢下降,后迅速下降,最后几乎不变,密度的分布几乎在介质表面的10µm厚度内;而静电场随着距离的增加单调下降,大约在300µm厚度时衰减到0.这是因为没有气体的存在,介质表面的击穿放电只存在二次电子的倍增过程,二次电子发射后介质表面形成的静电场是正值,电子被静电场牢牢地约束在介质表面. 在10 mTorr条件下,如图4(c)和图4(d)所示,电子密度有一个很小的峰值并在8—92µm内保持平稳,离子密度在8µm内迅速增加,后与电子一样保持平稳分布,但在92µm后两者同时迅速衰减至0附近.可以看出8µm内二次电子倍增主导放电,8—92µm气体电离发挥主要作用.静电场在8µm内由0.5 MV/m迅速降低至0 MV/m,最后在0 MV/m附近波动. 在500 mTorr条件下,如图4(e)和图4(f)所示,电子密度随距离的增加先下降到一个极小值(约8µm处),后增加到一个极大值(约16µm处),最后单调下降.Ar+密度随距离的增加先增加后下降,峰值中心约在16µm处.这是因为在介质表面10µm以内区域,二次电子倍增主导放电;在远离介质表面的区域,气体碰撞电离主导放电.静电场随距离的增加先从0.7 MV/m下降到−0.4 MV/m,再增加到0.3 MV/m左右,然后下降到0 MV/m,最后在其附近波动.静电场是由介质表面二次电子发射后积累的正电荷和气体电离产生的电子与Ar+的空间分布差异所决定的. 在10 Torr条件下,电子密度与Ar+密度空间分布基本一致,随着距离的增加先增加后下降,密度的峰值中心约在40µm处.这表明此时击穿放电主要由气体电离主导,而二次电子倍增过程被抑制.而静电场的分布为介质表面处为负向(指向介质表面方向),随着远离介质窗,静电场绝对值逐渐减小,后几乎在0附近波动. 在760 Torr条件下,电子密度与Ar+密度空间分布一致,在介质窗表面附近很低,在远离介质窗后逐渐升高,124µm之后波动变化.静电场在10µm以内几乎不变(−0.19 MV/m),然后绝对值逐渐减小到0 MV/m,最后在0附近波动.这是因为在如此高的气压下,二次电子发射完全被抑制,介质表面的击穿放电主要由气体电离主导.此外,在760 Torr条件下,电子密度和Ar+密度与10 Torr条件下的密度相比较低,这是因为在高气压下电子的自由程非常小,平均电子能量较低(6—7 eV),电离率较低,因此粒子密度较低. 比较图4(a)—(i),电子密度的峰值中心逐渐远离介质表面,例如在真空,10 mTorr,500 mTorr,10 Torr,760 Torr条件下,电子密度的峰值中心分别约在0,8,16,40,124µm.这是二次电子倍增和气体电离相互竞争的结果,二次电子倍增是在介质表面产生,而气体电离在等离子体体区内产生,可以看出,随着气压的升高,气体电离的优势逐渐增大. 图4 在(a),(b)真空,(c),(d)10 mTorr,(e),(f)500 mTorr,(g,h)10 Torr和(i),(j)760 Torr条件下微波周期平均的电子、Ar+及静电场Edc的空间分布Fig.4.The time-averaged spatial distributions of electron density,Ar+density and Edcat(a),(b)vacuum,(c),(d)10 mTorr,(e),(f)500 mTorr,(g,h)10 Torr and(i),(j)760 Torr. 图5给出了500 mTorr,f=2.85 GHz条件下,不同微波电场幅值下气体电离放电击穿发生的时间及电子密度峰值中心的位置.结果显示:在2.85 GHz微波下,随着微波电场幅值的增加,气体电离放电击穿发生的时间先下降后增加;而放电击穿后电子密度的峰值中心与介质表面的距离随着微波电场幅值的增加而单调下降,即微波电场幅值越大,气体电离放电击穿发生的位置越靠近介质窗表面.尤其当微波频率(GHz)是微波电场幅值(MV/m)的2倍左右时,气体电离放电击穿发生的时间较早.原因如图6(d)所示,当微波频率为微波电场幅值的2倍左右时,平均电子能量在二次电子倍增阶段变化范围是80—2150 eV,刚好处于图2所示的二次电子产额大于1的区间,且对应的二次电子产额数值较大,因此二次电子倍增饱和的过程最快.然而微波电场的幅值过低或过高,均会导致平均电子能量过低或过高,从而使得二次电子的产额减小,最终导致二次电子倍增饱和过程减缓,使得气体电离放电击穿的时间较晚. 图5 500 mTorr,2.85 GHz时气体电离放电击穿发生的时间点t0及放电击穿后峰值中心位置d0随微波幅值的变化Fig.5.The change of the time point of gas breakdown and the distance of the electron density peak away from the dielectric window with the microwave amplitude,at 500 mTorr,f=2.85 GHz. 图6 在500 mTorr,2.85 GHz及不同微波振幅幅值(a)0.2 MV/m,(b)0.5 MV/m,(c)1 MV/m,(d)1.425 MV/m,(e)2.82 MV/m,(f)5 MV/m下平均电子能量的时间演化规律Fig.6.Variations of the statistic electron energy with time t at different microwave amplitudes E0(a)0.2 MV/m,(b)0.5 MV/m,(c)1 MV/m,(d)1.425 MV/m,(e)2.82 MV/m and(f)5 MV/m,with microwave frequency and background gas pressure fixed at 2.85 GHz and 500 mTorr,respectively. 图7给出了500 mTorr,Erf0=2.82 MV/m条件下不同微波频率下气体电离放电击穿发生的时间及电子密度峰值中心的位置.结果显示:随着微波频率的增加,气体电离放电击穿发生的时间先下降后增加;而放电击穿后电子密度的峰值中心与介质表面的距离随着微波频率的增加是先升高后下降.同样值得注意的是,当微波频率(GHz)是微波电场幅值(MV/m)的2倍左右时,气体电离放电击穿发生的时间较早.产生这一现象的原因和图6所示的原因一致,如图8(c)所示,当微波频率是微波电场幅值的2倍左右时,在二次电子倍增阶段的平均电子能量正好处在二次电子产额最大的区间. 图7 500 mTorr,2.82 MV/m时气体电离放电击穿发生的时间点t0及放电击穿后峰值中心位置d0随微波频率的变化Fig.7.The change of the time point of gas breakdown and the distance of the electron density peak away from the dielectric window with the microwave frequencies,at 500 mTorr,Erf0=2.82 MV/m. 图8 在500 mTorr,2.82 MV/m及不同的微波频率(a)1.425 GHz,(b)2.85 GHz,(c)5.70 GHz,(d)10.00 GHz,(e)13.00 GHz,(f)15.00 GHz下平均电子能量的时间演化规律Fig.8.Variations of the statistic electron energy with time t at different microwave frequencies(a)1.425 GHz,(b)2.85 GHz,(c)5.70 GHz,(d)10.00 GHz,(e)13.00 GHz and(f)15.00 GHz,with the background gas pressure and microwave amplitude fixed at 500 mTorr and 2.82 MV/m,respectively. 本文针对HPM介质窗内侧氩气放电击穿过程建立了一维(1D3V)模型,并开发了PIC/MC程序,模拟研究了气压、微波电场幅值及微波频率对HPM介质窗放电击穿中等离子体的产生和演化过程.结果显示:在真空条件下,介质窗放电击穿只存在二次电子倍增过程;在低气压(10 mTorr,500 mTorr)和稍高气压(10 Torr)条件下,介质窗放电击穿过程由二次电子倍增主导放电转化为二次电子倍增和气体电离共存放电;在极高气压条件下(760 Torr),介质窗放电击穿由气体电离主导.同时给出了不同气压下电子、离子的密度和静电场的空间分布,结果显示,气压的增加使得电子密度的峰值中心逐渐远离介质窗.此外,在500 mTorr条件下当微波振幅增加时,气体电离放电击穿发生的时间先提前后延迟.这一现象通过次级电子发射模型进行了解释,即当微波电场幅值增大时,二次电子倍增过程中电子的平均能量增加,导致二次电子发射产额变大,倍增过程更易达到饱和,从而使得气体电离提前产生;然而当微波电场幅值过大时,电子的平均能量过高,导致二次电子产额反而降低,从而使得气体电离推迟产生.而且气体电离产生的电子密度峰值中心随着微波振幅的增加而逐渐靠近介质窗方向,即在高微波振幅条件下气体电离在更靠近介质窗的位置发生.同时,当固定微波振幅增加微波频率时,气体电离放电击穿的时间也是先提前后延迟;并且体电离产生的电子密度峰值中心随着微波频率的增加,先远离介质窗后靠近.尤其当微波频率(GHz)是微波振幅(MV/m)的2倍左右时,气体电离出现的较早.综上所述,在实际HPM应用过程中可以调节微波的振幅、频率及气压等,来实现推迟气体电离的出现,从而增加微波的传输效率. 感谢西北核技术研究所高功率微波重点实验室基金的支持和常超研究员对本论文的帮助.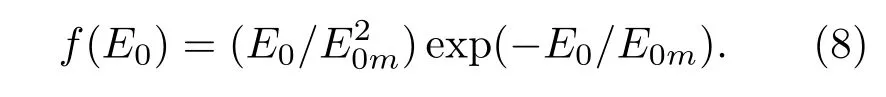
3 数值模拟结果与分析
3.1 气压对击穿放电的影响
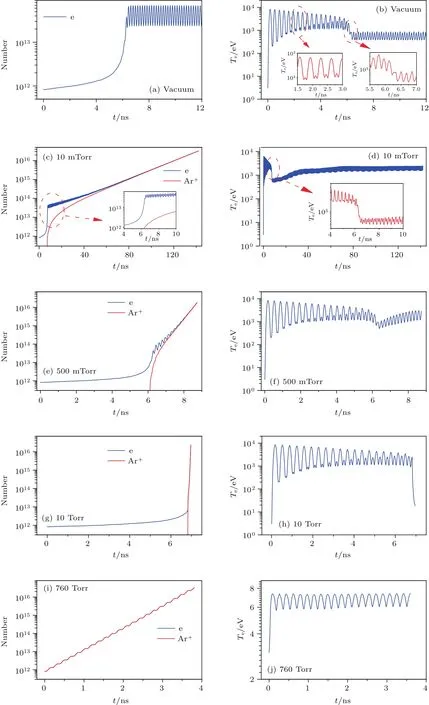
3.2 500 mTorr下微波幅值及微波频率对击穿放电的影响


4 结 论

