界面Dzyaloshinskii-Moriya相互作用下辐射状磁涡旋形成机制∗

董丹娜 蔡理† 李成 刘保军 李闯 刘嘉豪

1)(空军工程大学基础部,西安 710051)

2)(空军工程大学航空机务士官学校,信阳 464000)

(2018年7月20日收到;2018年9月3日收到修改稿)

1 引 言

近年来,关于涡旋(vortex)、斯格明子(skyrmion)、麦纫(meron)等自旋拓扑结构的研究[1−5]已经受到了越来越多的关注,因其具有天然的非易失性和良好的热稳定性而成为新兴存储载体的备选对象.2016年,Siracusano等在环形磁涡旋中引入了界面Dzyaloshinskii-Moriya相互作用(IDMI)这种界面手性的自旋-轨道相互作用[6−8],由于IDMI与交换能、各向异性能、静磁能之间的相互竞争,产生了一种全新的拓扑自旋结构[9]——辐射状磁涡旋(magnetic radial vortex)[10].辐射状磁涡旋由面内指向边界或中心的磁化矢量与核心位置垂直于盘面的磁化矢量组成.中心磁化矢量垂直于盘面向上(p=+1)或向下(p=−1)被定义为辐射状磁涡旋的极性(polarity).面内的磁化矢量指向边界(R=+1)或指向中心(R=−1)被定义为辐射状磁涡旋的辐射旋性(radial chirality).实现环形磁涡旋极性与旋性的同时翻转需要在隧道结中利用交变电流和磁场的共同作用[10−12],而辐射状磁涡旋由于IDMI引起拓扑约束导致的辐射状磁涡旋的固有属性,其极性与旋性可以被同时翻转,且驱动其极性翻转的极化电流较环形磁涡旋小一个数量级,该特征在利用完整隧道结磁阻信号变化来表征平行和反平行状态的应用方面具有明显优势[13−17].由于辐射状磁涡旋具有更好的热稳定性、驱动电流密度小、室温下翻转时间短等特点,因此可以应用于低功耗存储器件、磁阻存储器以及产生辐射状极化电流等方面.2018年,Karakas等[16]在Pt/CoFeB/Ti多层膜结构中发现了辐射状磁涡旋、斯格明子等的多种磁矩结构,验证了辐射状磁涡旋的存在,并提出了在超低功耗存储器件、逻辑电路、传感器技术等方面的应用前景.与此同时,本课题组提出了利用线性衰减垂直磁场实现辐射状涡旋核极性翻转的方法[18],与利用极化电流实现翻转的方法相比[10],其翻转时间能达到亚微秒级,同时在翻转过程中不改变涡旋核位置,更加利于磁阻信号的读取.该方法揭示了辐射状磁涡旋极性翻转过程的机理,可应用于高速数据存储器件等方面.上述研究为辐射状磁涡旋在自旋电子器件中的应用提供了理论和实验基础[19−21].

但以上研究并未详细讨论辐射状磁涡旋的形成过程,同时对于如何选取圆盘尺寸也缺乏理论依据和指导.而认识辐射状磁涡旋的形成过程对于了解辐射状磁涡旋的基本性质与形成时间和机理,以及利用辐射状磁涡旋构造存储器件等方面具有深远意义.因此,本文利用微磁学模拟方法研究了在IDMI效应下圆盘的直径、厚度以及IDMI强度的绝对值(|D|)对稳定形成辐射状磁涡旋的影响,为如何选择圆盘尺寸及|D|值以形成稳定的辐射状磁涡旋提供了理论依据.另外,通过讨论分析在不同磁矩初始态条件下辐射状涡旋的形成时间以及斯格明子数[22]、能量和磁矩的变化过程,发现了磁矩初始态对能否形成辐射状磁涡旋起着至关重要的作用,扩展了人们对于辐射状磁涡旋形成机制的认识,同时也为辐射状磁涡旋在自旋电子器件中的应用提供了理论基础.

2 器件结构与理论模型

本文研究对象的结构模型为图1(a)所示的Pt(5)/Ni80Fe20(1)/Ti(1)多层膜结构[16,23].这种多层膜结构可以在零偏置场及室温条件下通过坡莫合金(Ni80Fe20)与重金属层(Pt)的耦合,产生较大的IDMI作用,同时利用Ti(1)间隔层来避免IDMI作用衰减,在偶极场和IDMI作用下形成稳定的辐射状磁涡旋[6,24].我们采用的坡莫合金圆形纳米盘直径为d=80 nm,厚度为t=1 nm,模拟的剖分单元为1 nm×1 nm×1 nm.为了更好地理解辐射状磁涡旋的磁矩结构,图1(b)给出了辐射状磁涡旋的磁化矢量分布状态;图1(c)为沿着圆盘x轴方向直径上的磁化矢量在z轴方向上的分量mz.

辐射状磁涡旋的形成过程可以由微磁学模拟方法来进行研究,本文利用微磁学模拟软件MuMax3,对坡莫合金纳米圆盘中的磁化动力学过程进行了模拟.在MuMax3中Landau-Lifshitz-Gilbert(LLG)方程如下式[25]:

式中γLL为LLG旋磁比,α为LLG阻尼系数,Beff为有效场,即

方程(2)中,有效场Beff由退磁场Bdemag、交换场Bexch和IDMI场BDM组成,其中BDM可表达为:

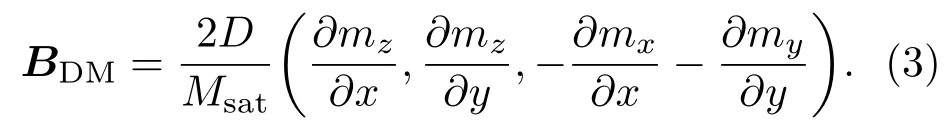
由IDMI场引起的能量密度为

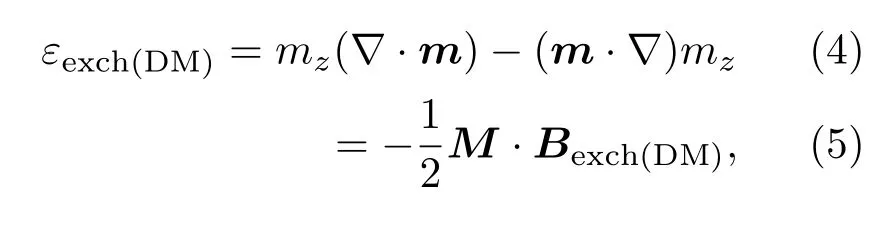
图1 结构模型与磁矩分布 (a)结构示意图;(b)磁矩分布图;(c)x轴方向直径上的z轴方向磁化分量Fig.1.Structural model and magnetic configurations:(a)Schematic diagram of a Pt/Ni80Fe20/Ti multilayer;(b)schematic diagram for the radial vortex state,the colors display the local mz;(c)the mzprofiles through the vortex core zone along the x-direction.

式中D表示IDMI强度,m为磁化强度减小量,M为Msat·m,T=0 K.在微磁模拟中,我们选择坡莫合金的经典参数:交换劲度常数Aex=1.3×10−11J/m,饱和磁化强度Msat=8×105A/m,磁晶各向异性常数K=0 J/m3,阻尼系数为α=0.01.

3 研究结果与讨论

3.1 圆盘直径对形成辐射状磁涡旋的影响

由于不同尺寸的纳米盘在强度不同的IDMI作用下,可以形成单畴、多畴、环形磁涡旋、辐射状磁涡旋和斯格明子等多种磁矩结构,所以纳米圆盘尺寸的选取对于IDMI作用下的磁矩结构有着非常重要的影响.而不同磁矩状态的形成,可以看成是静磁能、交换能以及IDMI能相互竞争产生的结果.交换能是在交换相互作用下,相邻原子的磁矩趋于平行排列的过程中产生的能量,是一种很短程的作用.而静磁能属于长程相互作用能,源于铁磁系统中原子磁矩之间的偶极-偶极相互作用.IDMI作用则是一种非对称的交换作用,源于自旋轨道耦合.首先我们针对纳米圆盘直径开展了模拟研究,通过微磁模拟发现,选取厚度t=1 nm的坡莫合金纳米盘,当直径小于3 nm时,由于圆盘尺寸较小,使得具有短程作用的交换能发挥主导作用,驱使相邻磁矩平行排列,圆盘形成单畴态;当直径大于600 nm时,由于圆盘尺寸增大,导致静磁能产生的长程作用增强,并占据主导地位,而静磁能在任意几何形状的物体中都倾向于使其分成磁畴,因此盘面形成多畴态.当圆盘直径变化范围为d=30—600 nm时,由于静磁能的长程作用与交换能的短程作用相互影响,使得IDMI作用在能量的竞争中发挥了主导作用,盘面形成稳定的辐射状磁涡旋.所以我们选取了直径d=60—600 nm之间11个不同的直径参数对稳定形成辐射状磁涡旋的|D|值范围进行了研究.

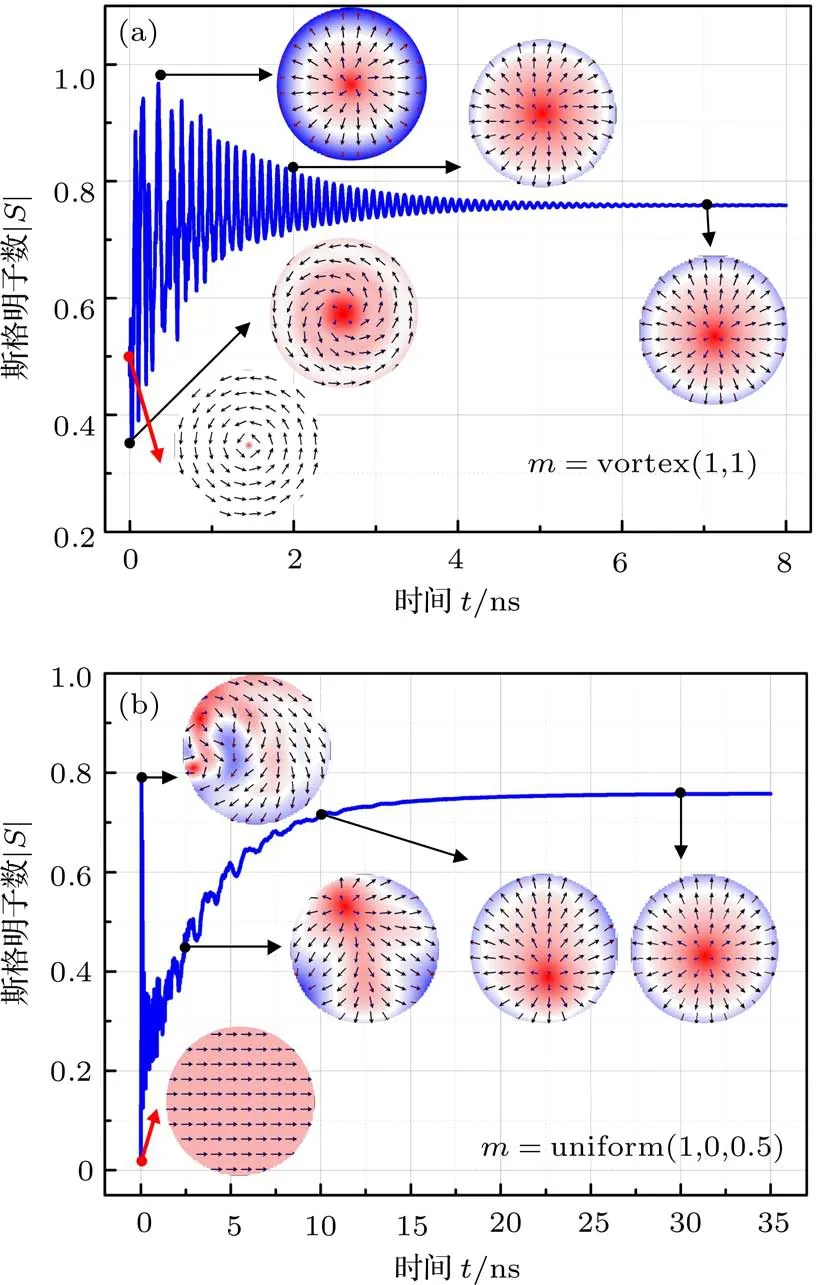
从图2可以看出,纳米盘的直径越小,能稳定形成辐射状磁涡旋的|D|值范围越大.这是由于随着纳米盘直径的减小,IDMI可以在较大的|D|值范围内保持主导作用,从而更容易形成稳定的辐射状磁涡旋.由此可见,适当减小圆盘直径,有利于在较小的|D|值下,形成辐射状磁涡旋.而在一定的直径范围内(150 nm

图2 纳米圆盘直径与形成稳定辐射状涡旋的|D|值之间的函数关系Fig.2.The IDMI value of nucleating a magnetic radial vortex as a function of diameter of nanodisk.

3.2 圆盘厚度对形成辐射状磁涡旋的影响

通过上一节的讨论,本节固定圆盘直径d=80 nm,针对稳定形成辐射状磁涡旋的纳米圆盘厚度进行研究.在模拟过程中,我们发现当圆盘厚度大于14 nm时,盘面的磁矩结构不再是辐射状磁涡旋,而是逐渐向斯格明子过渡的中间状态.所以,在模拟中选取了厚度在t=1—13 nm之间的8个不同值,来讨论圆盘厚度对形成稳定辐射状涡旋的影响.

图3显示,随着圆盘厚度的增加,形成稳定辐射状磁涡旋的|D|值范围逐渐减小,|D|最小值明显增大.这是由于在圆盘厚度增加的过程中,静磁能和交换能在竞争中的作用逐渐增强,需要增大|D|值来保持IDMI能的主导作用,从而生成稳定的辐射状磁涡旋.当厚度较小时,|D|值过大,盘面会形成多畴态;当厚度大于6 nm时,随着|D|值的增大,在交换相互作用、静磁能及IDMI能的相互竞争下,辐射状磁涡旋中心及边缘的极性区域逐渐增大,磁化状态向斯格明子态转化,因此|D|最大值增长幅度较小.结果表明,辐射状磁涡旋不仅存在于厚度t=1 nm的圆盘中,当圆盘厚度t=13 nm,|D|值取2.6—3.3 mJ/m2之间时,辐射状磁涡旋也可以稳定存在.所以在适当的|D|值范围内,当圆盘厚度增加一个数量级时,也可以形成稳定的辐射状磁涡旋.由此可见,辐射状磁涡旋可以在较大的圆盘厚度范围内形成,但随着圆盘厚度的增大,形成辐射状磁涡旋的|D|最小值变大,因而|D|值范围逐渐减小.当|D|值低于最小值,盘面形成环形涡旋态;当|D|值高于最大值时,盘面形成多畴态或斯格明子态.

图3 纳米圆盘厚度与形成稳定辐射状涡旋的|D|值之间的函数关系Fig.3.The IDMI value of nucleating a magnetic radial vortex as a function of thickness of nanodisk.

3.3 不同初始态对辐射状磁涡旋形成过程中斯格明子数的影响

辐射状磁涡旋的成核过程就是饱和磁化状态的弛豫过程[10],所以不同的初始状态对辐射状磁涡旋的形成过程影响较大.斯格明子、单畴、环形磁涡旋以及辐射状磁涡旋等不同磁矩结构的斯格明子数均不相同,例如辐射状磁涡旋的斯格明子数为0.7—0.9,而环形磁涡旋的斯格明子数则为0.5,因此,典型的磁矩结构均可用斯格明子数(skyrmion number)进行表征:

式中S为斯格明子数,q为拓扑密度[26].首先选取两种不同的磁矩结构作为初始态,第一种是极性为p=+1(垂直盘面向上),旋性为c=+1(逆时针方向)的环形磁涡旋态;第二种是x轴方向上的磁化分量mx=1,z轴方向上的磁化分量mz=0.5的单畴态,分别对两种初始态形成辐射状磁涡旋的过程进行仿真,选取纳米盘直径d=80 nm,厚度t=1 nm,D=−2.8 mJ/m2,本节采用的IDMI强度参数为负值.由于当参数D取正时,斯格明子数的变化规律与取负时基本相同,但磁化状态的极性或旋性与取负时相反,所以本文只讨论IDMI强度参数为负值的情况.

由图4(a)可见,环形涡旋初始态的斯格明子数为S=0.5,模拟开始后,斯格明子数围绕平衡位置0.77开始振荡,并在t=0.2 ns时刻达到0.55的最大振荡幅度,t=0.35 ns时刻,斯格明子数达到峰值S=0.97,这是由于IDMI边界条件所引起的圆盘边缘部分的磁矩振荡导致的[27],而各项能量的振荡变化,则是产生磁化矢量振荡的根本原因.峰值过后,随着时间的推移,斯格明子数的振荡幅度逐渐减小,最终落到平衡位置,盘面的磁矩结构也由首尾相接的环形状态逐渐指向圆盘边缘.在t=2 ns时,斯格明子数振荡幅度为0.1,由磁矩图可以看出,盘面的磁矩方向基本全部指向边缘,辐射状磁涡旋基本形成.当t=7 ns时,斯格明子数为0.77并保持不变,辐射状磁涡旋稳定形成.

图4 形成辐射状涡旋过程中斯格明子数随时间的演化(红色箭头指向初始态的磁矩分布) (a)初始态为环形涡旋;(b)初始态为单畴Fig.4.Temporal variation of the skyrmion number in the magnetic radial vortex nucleation process(the red arrow points to the initial state):(a)The initial state is the circular vortex;(b)the initial state is the uniform state.

由图4(b)可以发现,单畴初始态的斯格明子数为S=0,加入IDMI作用,斯格明子数开始振动,并在t=0.04 ns时刻达到峰值S=0.79,此时盘面出现了无序的多畴态,并在5 ns的时间内保持极性相互竞争的多畴状态.斯格明子数经过短暂振动后,以较小的振动幅度逐渐增大,并趋于稳定.通过观察磁矩图,发现在t=2.5 ns时,涡旋核已在圆盘边缘形成,并在波动中逐渐向中心靠拢.当t=30 ns时,涡旋核固定在圆盘中心位置,斯格明子数达到0.77并保持不变,辐射状磁涡旋稳定形成.本文将在3.4节中详细分析这两种不同初始态形成稳定辐射状磁涡旋过程中的能量变化.

对两种初始态进行对比,发现以环形磁涡旋为初始态的变化过程从开始到稳定形成辐射状磁涡旋只需要7 ns,而以单畴为初始态则需要30 ns.这是由于以环形磁涡旋为初始态的形成过程中,涡旋核虽有微小变化,但始终稳定存在,变化过程的主体是形成面内辐射状磁矩;而以单畴为初始态的形成过程中,涡旋核的生成并稳定在中心位置是变化过程的主体,因而其辐射状磁涡旋的形成时间是前者的4倍.这说明在形成辐射状磁涡旋的过程中,涡旋极性的形成比辐射旋性的形成时间更长.从上述仿真结果可以看出,不同初始态形成辐射状磁涡旋的斯格明子数变化过程明显不同,且磁矩变化与斯格明子数变化基本同步,所以可以将斯格明子数的变化规律作为区分不同初始态以及判断辐射状磁涡旋是否形成的条件.另外,在模拟过程中还发现z轴方向无磁化分量的单畴初始态,无论|D|取何值,盘面都无法形成辐射状磁涡旋,这说明初始态z轴方向的磁化分量对于涡旋核极性的形成起着决定性作用.

3.4 不同初始态对辐射状磁涡旋形成过程中能量变化的影响

形成稳定辐射状磁涡旋的过程可以看成是静磁能、交换能和IDMI能相互竞争、总能量不断衰减并最终趋于稳定的过程.为了更深入地理解辐射状磁涡旋的形成机制,结合3.3节斯格明子数的变化过程,我们对不同初始态形成过程中的能量变化进行了对比研究.选取与3.3节一致的两种磁矩结构作为初始态,纳米盘直径、厚度以及|D|值等参数也与3.3节相同.分别对两种不同初始态形成辐射状磁涡旋的过程进行微磁学模拟.

图5 形成辐射状涡旋过程中能量随时间的演化 (a)初始态为环形涡旋;(b)初始态为单畴Fig.5.Temporal variation of the energy in the magnetic radial vortex nucleation process:(a)The initial state is the circular vortex;(b)the initial state is the uniform state.

由图5(a)中可以看出,环形涡旋初始态的静磁能和交换能开始振荡且振幅逐渐减小,在t=0.3 ns时振幅达到最大,在t=3 ns时,静磁能和交换能基本稳定.总能量在变化过程中逐渐减小,在t=2 ns时总能量达到E=−2×10−19J,总能量在静磁能、交换能以及IDMI能的竞争过程中不断衰减,最终系统能量达到平衡状态,总能量衰减到最小值.

由图5(b)可得,单畴为初始态时,静磁能和交换能在经过短暂的波动后,在t=0.4 ns时就已落到了稳定值附近,又经过微小波动,在t=1.5 ns时,达到稳定状态.而总能量的衰减速度很快,在t=0.08 ns时就已衰减到了E=−1×10−19J,在t=1 ns时,达到稳定值E=−2×10−19J.

对两种初始态进行对比得出,以环形磁涡旋为初始态的能量衰减时间(t=2 ns)是以单畴为初始态能量衰减时间(t=1 ns)的两倍,可见以环形磁涡旋为初始态时,能量达到稳定状态所需的时间更长.对比3.3节内容,可以看出虽然二者的初始态不同,但斯格明子数的变化趋势均是由各项能量在竞争过程中的变化决定的.我们发现在以环形磁涡旋为初始态的变化过程中,能量衰减到最小值时,辐射状磁涡旋也基本形成.而当单畴初始态的能量衰减到最小值时(t=1 ns),纳米盘面形成了不在中心位置的涡旋核,且面内磁矩方向已基本形成辐射状.所以在形成稳定辐射状磁涡旋的过程中,能量变化主要与涡旋核极性的生成和面内磁矩方向有关,而与涡旋核在盘中的位置基本无关.

4 结 论

本文通过微磁学模拟方法研究了能够形成辐射状磁涡旋的圆盘尺寸及IDMI强度范围,探讨了不同初始态的辐射状磁涡旋形成机制及磁矩的变化过程.相关结果表明,在面内静磁能、交换能以及IDMI能的竞争作用下,在一定范围内,纳米盘直径越小,能稳定形成辐射状磁涡旋的|D|值范围越大,并且直径为250 nm时,圆盘形成辐射状磁涡旋的|D|取值范围较大,因此可以通过选择合适的圆盘直径以满足对|D|的取值要求.同时发现,选取适当|D|值时,在较大范围内,改变圆盘尺寸不会影响辐射状磁涡旋的稳定生成.辐射状磁涡旋不仅存在于厚度t=1 nm的圆盘中,当圆盘厚度增加一个数量级时,在一定的|D|值范围内,也可以稳定形成辐射状磁涡旋.在对形成辐射状磁涡旋的模拟过程中还发现,以单畴为初始态的形成时间比以环形涡旋为初始态的形成时间更长,这表明形成辐射状磁涡旋极性比形成辐射旋性需要更长时间.不同初始态下形成辐射状磁涡旋的斯格明子数变化过程明显不同,且磁矩变化与斯格明子数变化基本同步,所以可将斯格明子数的变化规律作为区分不同初始态以及判断辐射状磁涡旋是否形成的条件.磁矩初始态必须具有z轴方向的磁化分量才能形成辐射状磁涡旋.同时发现,在形成稳定辐射状磁涡旋的过程中,以环形磁涡旋为初始态的能量衰减时间比以单畴为初始态的衰减时间更长,且能量变化主要与涡旋核极性的生成以及面内磁矩方向的改变有关,而与涡旋核在盘中的位置基本无关,这为我们提供了可以利用辐射状磁涡旋核进动实现自旋纳米振荡器的新思路.本文研究结论为在形成辐射状磁涡旋时选取IDMI强度和软磁纳米圆盘尺寸提供了重要的参数选择依据,同时扩展了人们对辐射状磁涡旋形成机制和磁矩变化过程的认识,也为下一步辐射状磁涡旋在自旋电子器件中的应用提供了重要的理论支撑.