同轴传输线微放电的统计理论稳态建模及敏感区域计算∗

林舒 夏宁 王洪广 李永东 刘纯亮

(西安交通大学电信学院,电子物理与器件教育部重点实验室,西安 710049)

(2018年7月10日收到;2018年9月21日收到修改稿)

1 引 言

微放电[1,2]是受微波场交互作用而在真空环境下产生的二次电子倍增效应,常发生于空间与加速器应用中的大功率微波器件,如微波开关、多工器与滤波器等[3−5].近年来,世界各航天强国相继开展火星、金星以及太阳系其他小行星等探测计划,而国内外的天基互联网与星链计划也对卫星通信与遥感技术的发展提出了更高的要求.作为星地通信与目标控制的惟一纽带,星载通信系统的运行稳定性关乎整个空间任务的成败.一方面,受空间远距离通信衰减的影响,星载通信系统必须尽可能提高功率容量以保证通信质量.同时,空间有效载荷还要求尽可能地减小星载通信系统的质量与体积,以降低空间探测成本与设备研发周期,但这些趋势都显著增加了微波器件中发生微放电的风险.作为空间微波器件的主要失效模式,微放电轻则造成信号失谐与噪声干扰,重则导致气体放电并烧毁器件乃至通信系统,这也使得微放电成为限制空间通信技术发展的重要因素[6].因此,地面研制阶段须准确预测微波器件的微放电阈值,并进行充分的抗微放电性能分析和设计,以尽可能降低在轨微波器件的微放电风险[7].

作为微放电研究的重要理论方法,统计理论可以充分考虑电子的出射与渡越随机性[8],因而能够实现准确的微放电机理分析与阈值预测.迄今为止,统计理论在微波器件的单、多载波微放电以及微波介质窗的倍增击穿研究[9−11]中都有非常广泛的应用.最早于2004年,Vdovicheva等通过推导微放电倍增条件的积分方程,构建得到微放电统计理论的稳态模型,由此实现平行平板传输线[12]与矩形波导[13]微放电的阈值计算与分析,但它只考虑了双边碰撞产生的二次电子发射.为此,Anza等在其基础上构建用于模拟微放电动态发展过程的非稳态模型[14],并将其进一步推广至平行平板传输线的多载波微放电分析中[15].非稳态模型由于同时考虑单边和双边碰撞的影响,因而能够获得更高的微放电阈值计算精度.国内方面,浙江大学的宋庆庆等[16]也在其基础上将统计理论与随机漫步理论结合,由此实现矩形波导多载波微放电的非稳态建模与分析.同时为研究非对称的微放电过程,本课题组又将非稳态建模推广到同轴传输线微放电的机理分析与阈值计算中[17].

相比而言,非稳态模型虽然具有相对较高的阈值计算精度,但需要耗费大量计算时间模拟微放电的动态演化过程.因此,现有的非稳态模型主要用于离散频点处同轴传输线微放电阈值的计算与比对,仍不适用于大范围的微放电敏感区域计算.稳态模型则是通过微放电的稳态方程直接确定电子数目的变化趋势,避免重复计算大量电子的运动轨迹,因而能够实现更高的阈值计算效率.而在材料表面处理研究[18−20]方面,兼具高阈值计算精度与效率的稳态模型也可作为其微放电抑制效果的有效评估方法.为此,本课题组对平行平板微放电的稳态建模过程进行了改进,使其能够兼顾微放电过程中的单边碰撞,由此解决了稳态模型阈值计算精度低的问题[21].同时为更切合实际的工程应用需求,本课题组也曾对同轴结构微放电进行了近似的稳态建模[22],但由于未考虑其微放电过程的非对称性,所得的阈值计算精度不甚理想.因此,当前亟需通过改进稳态建模构建精确有效的同轴传输线微放电阈值分析方法,并在其基础上研究平行平板与同轴传输线的结构差异以及器件镀膜材料对微放电阈值的影响规律,由此为实际工程中“免微放电”微波器件的设计与优化提供必要的参考.

鉴于此,本文在同时考虑微放电过程中单边与双边碰撞影响的情况下,推导同轴结构中内、外导体处电子出射相位分布所满足的稳态方程组,并提出一种通用的联立迭代求解方法,构建同轴结构微放电统计理论的稳态模型.同时,使用该模型分别计算银(Ag)、铜(Cu)、铝(Al)与阿洛丁(Alodine)等常用工程镀膜材料的同轴传输线微放电敏感区域以及不同径比下的同轴传输线微放电阈值,并与欧空局(ESA)的微放电实验结果进行对比验证.最后与平行平板传输线微放电的敏感区域对比,分析平行平板与同轴结构微放电的阈值差异.

2 模型简介

确切地说,完整的统计理论建模过程实际上包括两个主要步骤.首先,推导电子轨迹的解析表达式,并在其基础上构建联合概率密度函数,由此实现电子渡越时间概率分布的求解计算;然后,通过微放电倍增过程的稳态或非稳态描述,计算给定条件下电子数目的变化趋势,进而确定微放电的阈值与敏感区域.需要说明的是,微放电统计理论研究关注的是微放电建立的初始阶段,因此下面的电子动力学分析会忽略空间电荷效应的影响.

2.1 基本方程及定义

图1为同轴传输线的径向剖面示意图,其外导体的内半径和内导体的外半径分别用Ro和Ri表示,两者比值(后面统一简称为径比)为γ=Ro/Ri,同时内、外导体之间的距离为d=Ro−Ri.考虑到工程常用性以及现有同轴传输线微放电的实验对象,本文默认选取50 Ω特征阻抗的同轴传输线为研究对象,其物理尺寸为Ro=3.55 mm与Ri=1.54 mm,同时假设同轴传输线中的微波模式为TEM模,电子所受磁场力远小于电场力,因此忽略磁场分量对电子运动的影响.另外,由于电子碰撞动能主要来自径向电场Er的加速作用,所以这里仅分析径向上的一维电子运动,而电子随时间t变化的径向位置r则可以通过如下方程求解:

其中me和e分别表示电子质量/kg与电量/C;Vrf是微波场的电压幅值/V;ω是微波场的角频率/rad·s−1.

图1 同轴传输线径向剖面示意图Fig.1.Diagrammatic cross-sectional view of coaxial transmission lines.

从数学角度上看,上述常微分方程并没有精确的解析解.但在物理角度上,除时谐微波场使电子做快速振荡运动以外,场分布非均匀性引起的势能梯度还对电子产生米勒力的作用[23],它会推着电子同时朝外导体做缓慢漂移运动.因此采用微扰法(详见文献[24])可以近似推导得到如下电子轨迹的解析表达式:

式中的主要参数有

其中φs为电子出射相位;τ为电子碰撞时的相位变化量,其在广义的时间量纲上又指电子的渡越时间;u,ηs和ηf分别表示归一化的电子出射速度(υs)、出射位置(rs) 与碰撞位置(rf),等于υs/υω,ωrs/υω和ωrf/υω,并有υω=eVrf/meωrslnγ.由于电子的出射和碰撞位置均有可能为同轴结构的内导体或外导体处,所以这里将电子轨迹分为外导体处出射的单边碰撞ξoo(rs=Ro与rf=Ro)、外导体处出射的双边碰撞ξoi(rs=Ro与rf=Ri)、内导体处出射的双边碰撞ξio(rs=Ri且rf=Ro)以及内导体处出射的单边碰撞ξii(rs=Ri且rf=Ri)四种不同的类型.

另外,上述推导可以使用参数ηi来衡量电子轨迹表达式的计算精度,其中ηi等于ηs(rs=Ri).为确定近似轨迹表达式的适用范围,下面分别使用电子轨迹表达式((2)式)与四阶龙格-库塔方法计算不同参数条件下的电子运动轨迹.为便于区别,下面将这两种方法得到的电子轨迹分别简称作解析轨迹与数值轨迹.由于龙格-库塔方法的求解精度非常高,所以数值轨迹可以作为真实的电子轨迹进行参考比较.图2给出了不同ηi值下四种轨迹类型的解析轨迹与数值轨迹,其横坐标与纵坐标分别为电子的相位变化量∆φ与归一化的电子运动位置∆ξ.可以看到,在ηi=10时,电子运动过程中的快速振荡幅度远小于缓慢漂移的幅度,电子的解析轨迹与数值轨迹符合得很好;但随着ηi的减小,快速振荡运动变得越来越剧烈,电子的碰撞也逐渐变得由快速振荡运动所主导,同时微扰法的成立条件也逐渐失效,解析轨迹与数值轨迹之间的偏差也越来越大;在ηi=3时,电子在渡越过程中的轨迹偏差已经较为明显,但碰撞发生时,两种方法计算的电子渡越时间偏差仍可以接受;而当ηi减小至1.25时,两种轨迹之间已经表现出非常大的偏差.综上所述,只有满足ηi>3条件,近似的电子轨迹表达式才具有可接受的精度,同时后面统计理论的稳态建模也不会在计算微放电阈值时产生较大的误差.

图2 不同ηi值下不同类型解析轨迹与数值轨迹的对比Fig.2.Comparison of analytical and numerical trajectories for different ηi.

从本质上看,电子的出射随机性是造成上述电子运动轨迹差异的重要因素.假设电子的出射速度u满足如下麦克斯韦分布:

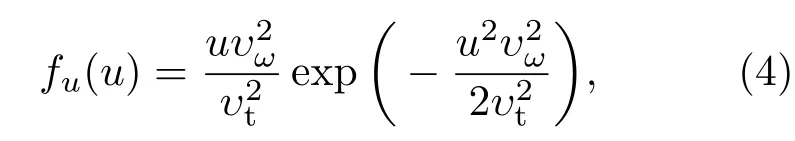
式中υt表示平均出射速度,可以通过平均出射动能Et(通常取1.5 eV)计算得到.基于上述推导的轨迹表达式,同轴结构微放电中的联合概率密度函数G(τ|φs;ξ)则可以写为

与平行平板微放电中一样,其在物理意义上同样表示以相位φs出射的电子在经历渡越时间τ后以轨迹ξ(ηs,ηf)发生碰撞的概率密度.上式中u=g(τ|φs;ξ),只是假定的表达式. 从(2)式中可以看到,电子轨迹的解析表达式过于复杂,因而无法由其转换得到u关于τ的显式表达式.因此,这里引入一种基于隐式关联性的联合概率密度函数构建方法,用于求解同轴结构微放电中电子渡越时间的概率分布.在实际计算过程中,任意给定的渡越时间τ所对应的出射速度u可以通过电子轨迹的表达式数值求解得到,(5)式右边的求导项则可以改写为如下隐式形式:

需要注意的是,上式求解过程应当筛选掉单个出射速度u对应多个渡越时间τ的情况,其本质上是电子的快速振荡运动在边界处发生的非物理碰撞.

2.2 统计理论稳态建模

结合上述联合概率密度函数,本节通过推导内、外导体处电子出射相位分布所满足的积分方程组,构建同轴结构微放电统计理论的稳态模型.为便于理解,方程推导从电子数目与出射相位分布随电子更新换代的变化过程出发,同时考虑同轴结构微放电的非对称性.假设微放电过程中经历过相同碰撞次数所产生的二次电子为同代电子,内、外导体处第l−1代电子的数目分别表示为和,而相应的出射相位分布函数为和.这些电子碰撞后产生第l代二次电子的数目和将分别满足

与

与

其中K函数写为

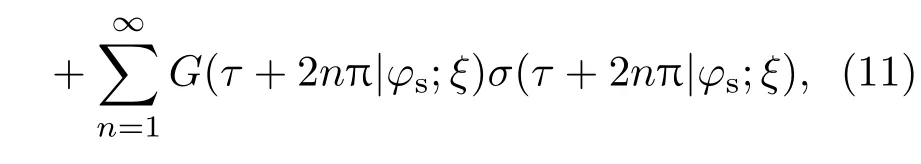
式中θ(τ|φs)为阶跃函数,而σ(τ|φs;ξ)为材料的二次电子发射系数(SEY)函数,它是通过电子轨迹表达式的导数求解电子碰撞动能,再结合描述SEY分布的唯象模型构建得到.此外,(9)式与(10)式右边的第一项和第二项分别代表单边和双边碰撞所产生的二次电子发射,由于双边碰撞产生二次电子的出射方向发生了变化,所以相邻两代电子的出射相位分布之间需要引入半个周期的相位偏移.

从本质上看,场分布的非均匀性使得同轴结构中形成非对称的微放电过程,而内、外导体处的电子出射相位也会形成不同的稳态分布,所以平行平板微放电稳态建模中将其处理为第二类Fredholm积分方程的方法就不再适用.早前的研究[22]虽然基于这种求解方法实现了近似的稳态建模,但由于忽略了同轴结构微放电过程的非对称性,其最终得到的微放电阈值计算精度也会受到影响.鉴于此,这里为上述稳态积分方程组引入如下联立迭代求解方法.首先,假设内、外导体处初始(首代)电子的数目分别为和,它们的出射相位分布和都是均匀的,将这些参数代入(9)与(10)式后,即可分别求得内、外导体处首代二次电子的数目与出射相位分布;继续迭代求解后续代数电子的相应参数,直至内、外导体处电子出射相位分布趋于稳定.在实际的迭代求解过程中,当内、外导体处相邻两代电子出射相位分布的总相位偏移率不超过10−4时,即可判定同轴结构中的微放电过程已经发展至稳态.

图3(a)和图3(b)中分别给出了同轴结构发生微放电时内导体与外导体处电子出射相位分布与相邻两代电子数目比值随电子代数更迭的变化情况,其中f=1.6 GHz与Vrf=280 V.可以看到,同轴结构中的微放电过程中发生了明显的相位聚焦现象.随着电子碰撞发生,内、外导体处的电子出射相位分布迅速朝有利区间[−π/4,π/2]聚拢并最终达到稳定,同时相邻两代电子数目的比值在经历初始振荡后也很快趋于恒定.另外,内、外导体处电子出射相位的稳态分布并不相同,由于内导体处的电场强度要高于外导体处,所以内导体处的相位聚焦效果更强.同时,上述方程组求解只进行了数次(十次以内)迭代后,内、外导体处电子的出射相位分布就已经达到稳态.因此,同轴结构微放电的稳态建模采用这种联立迭代方法可以快速确定电子数目的变化趋势.

此外,图4还给出了不发生微放电(Vrf=200 V)、临界微放电(Vrf=245 V)以及发生微放电(Vrf=280 V)三种不同情况下同轴结构内导体与外导体处电子出射相位的稳态分布.观察发现,微波场电压的升高使得电子出射相位分布更加集中.因为在强电场的作用下,以有利相位出射的电子可以得到更多的动能,并碰撞产生更多二次电子,而以非有利相位出射的电子则更多地被“淘汰”掉,从而产生更显著的相位聚焦效应.同时,相比于内导体处电子出射相位分布的微弱变化,外导体处电子出射相位分布的变化更为明显,这也间接说明外导体处的电子碰撞情况主导着同轴结构微放电的整体发展趋势,这与非稳态建模的分析结果一致.

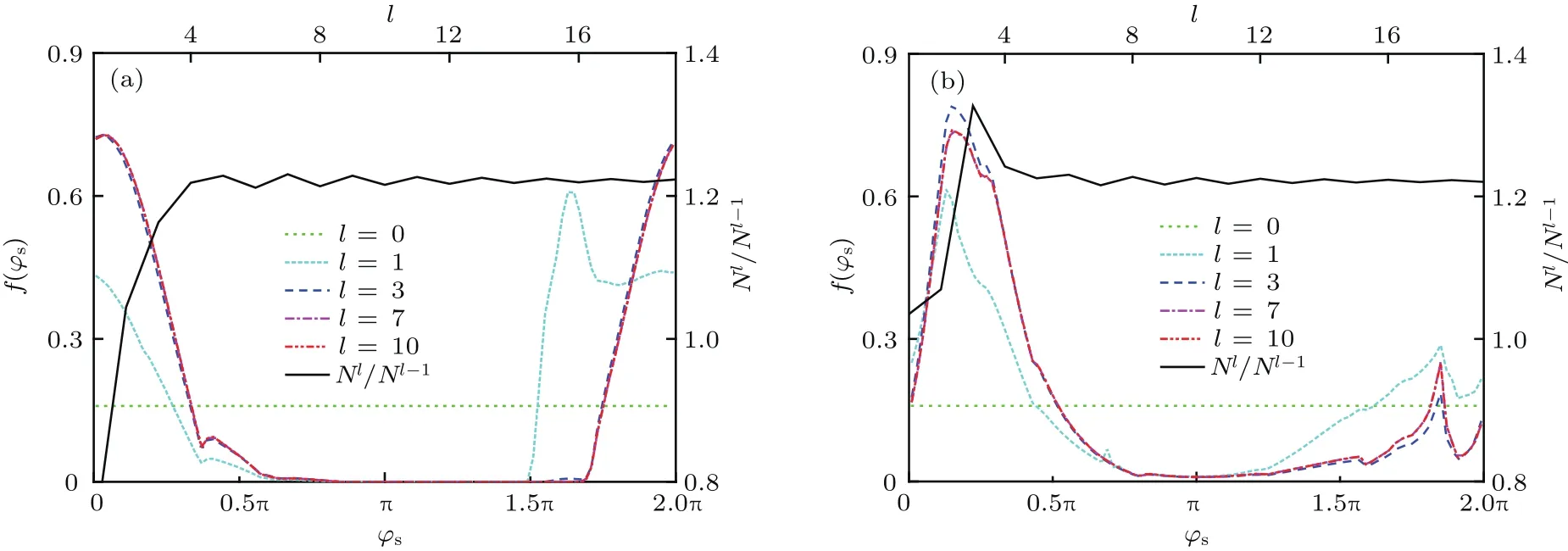
图3 同轴结构内导体(a)与外导体(b)处电子出射相位分布与相邻两代电子数目比值随电子代数更迭的变化情况Fig.3.Convergence of electron emission phase distribution and electron population ratio at the inner conductor(a)and outer conductor(b)of coaxial geometry along with iteration process.

图4 不同微放电情况下同轴结构中内导体(a)与外导体(b)处电子出射相位的稳态分布Fig.4.Steady distribution of electron emission phase at the inner conductor(a)and outer conductor(b)of the coaxial geometry along with the iteration process.

最后,为准确判定微放电的阈值电压,统计理论稳态建模通过微放电趋于稳态时相邻两代电子数目的比值计算下面的有效二次电子倍增率σeff,以此表征微放电的发生程度.上标“st”表示微放电达到稳态,而根据σeff的大小就可以判断是否会发生微放电.当σeff>1时,微放电过程中的总电子数目呈指数倍增,明显会发生微放电;σeff<1则表示总电子数目随碰撞的发生而逐渐减少,因而不发生微放电;而σeff=1则对应于发生微放电的临界情况,此时的微波场电压即为微放电的阈值电压.

3 同轴传输线的敏感区域计算与分析

结合2.1节中构建的联合概率密度函数,再根据2.2节中推导的解析稳态方程及引入的联立迭代求解方法,就可以计算不同参数条件下的有效二次电子倍增率,由此计算得到同轴结构微放电的敏感区域,进而实现器件结构与材料对微放电阈值影响的规律分析.为此,本节采用上述稳态模型分别计算银、铜、铝与阿洛丁等工程常用镀膜材料[25]的同轴传输线微放电敏感区域,各材料的结果具体如图5—图8所示.另外需要强调的是,上述敏感区域计算统一采用默认尺寸的同轴传输线,而且这些材料的SEY分布也都采用修正的Vaughan模型[26]拟合,具体如下面的分段公式所示.

另外,图5—图8中还给出了ESA通过实验测量得到的相同材料同轴传输线的微放电阈值结果,以便于进一步的对比与分析.由于稳态建模采用的是近似的电子轨迹表达式,其误差会影响到微放电阈值的计算精度,而ηi作为电子轨迹表达式精度的衡量因子,其数值越高,电子轨迹的计算误差越小,所预测的微放电阈值也越精确.如前所述,近似的电子轨迹表达式只有在ηi>3.0时才有可接受的精度,因此下面分析中将满足该条件的右下方敏感区域当作可信区域,而图中的黑色虚线正好对应由ηi=3.0条件决定的可信区域边界.

表1 不同材料SEY的Vaughan模型拟合参数Table 1.Fitting parameters of Vaughan model for different material’s SEY.

图5 银材料镀膜同轴传输线的微放电敏感区域Fig.5.Multipactor suscepbility zone of coaxial transmission lines for silver coating.

可以看到,材料SEY特性的差异使得上述材料的微放电敏感区域之间表现出明显的不同.相对而言,银、铝与铜材料由于具有较高的σm值与较低的E1值,更容易产生二次电子发射,从而形成更大的微放电敏感区域,而右下方的敏感区域也更多地进入可信区域内,所以由稳态模型计算的微放电阈值与实验结果之间也符合得更好.然而,SEY整体分布较低的阿洛丁则表现出相对较高的微放电阈值,尤其在一阶敏感区域处.由于左侧三个频点处敏感区域的边界明显超出可信区域,因此微放电阈值的预测结果也表现出较大的误差,但对于高阶敏感区域而言,由稳态模型计算的微放电阈值在大多数频点处与实验结果则符合得很好.

图6 铝材料镀膜同轴传输线的微放电敏感区域Fig.6.Multipactor suscepbility zone of coaxial transmission lines for aluminium coating.

另外,非稳态模型虽然也可以实现同轴结构微放电的机理分析与阈值预测,但同轴结构中的电子在米勒力作用下更可能发生长程单边碰撞,因此非稳态建模需要耗费更多的计算时间模拟微放电的实时演化过程.而稳态建模可以基于联立迭代方法直接求解上述稳态方程组,从而实现同轴结构微放电阈值与敏感区域的快速计算.对比发现,使用非稳态模型求解各实验频点处微放电阈值的计算耗时约是使用稳态模型的3—5倍,因此稳态建模也为后面微放电敏感区域的对比分析提供了高效实用的计算工具.

同时,为分析平行平板与同轴结构微放电的阈值差异,上述敏感区域图中还给出了不同材料的平行平板微放电敏感曲线(σeff=1),即敏感区域的边界,而平行平板的微放电统计理论建模及敏感区域计算方法参见文献[21].对比发现,平行平板微放电的一阶与三阶敏感区域相互分离,但与其相比,同轴结构微放电的敏感区域则较为集中,尤其三阶敏感区域相对向左偏移,并与一阶敏感区域出现明显的交叠,这与早期Woo[27]在同轴结构微放电实验中得到的阈值规律相符合.

图7 铜材料镀膜同轴传输线的微放电敏感区域Fig.7.Multipactor sensitivity zone of coaxial transmission lines for copper coating.

图8 阿洛丁镀膜同轴传输线的微放电敏感区域Fig.8.Multipactor suscepbility zone of coaxial transmission lines for alodine coating.

此外,中间几阶敏感区域的下边界也不像平板微放电中那样平滑,并表现出较大波动,这使得两种结构微放电阈值的相对大小交替变化.可以看到,三阶敏感区域左侧的同轴结构微放电阈值要小于平行平板微放电阈值,但其右侧处却表现出相反的规律.同时在高阶敏感区域处,两种结构的微放电阈值差异情况对于不同材料也是不一样的.对于银、铜与铝材料而言,平行平板与同轴结构的微放电阈值在高阶敏感区域处较为一致,但阿洛丁中的阈值差异则较为显著.

为分析SEY参数对微放电敏感区域大小的影响,图9绘制了上述镀膜材料的同轴传输线微放电敏感曲线.可以看到,这些材料的微放电阈值大小顺序为Cu

图9 不同镀膜材料的同轴传输线微放电敏感曲线对比Fig.9.Comparison of multipactor suscepbility curves of coaxial transmission lines for different coating materials.

图10分别给出了1.15,1.6与3.0 GHz三个不同频率下微放电阈值电压与功率随同轴结构径比γ的变化曲线.为准确分析径比变化对微放电阈值的影响,我们在改变同轴结构径比时保持其内径与外径之间的差值不变,即d恒等于2.01 mm.另外要说明的是,本文的统计理论建模基于近似推导的电子轨迹表达式,其在计算高径比的同轴传输线微放电阈值时具有较大的误差,因此这里只分析了[1.2,4.2]范围内的径比变化对同轴传输线微放电阈值的影响规律.可以看到,在径比小于2.5时,同轴传输线的微放电阈值电压会随着径比的增加而缓慢降低,但由于其特征阻抗也随之升高,同轴传输线中发生微放电的阈值功率随之迅速减小.然而当径比增加到一定数值(2.7—3.5之间)时,微放电阈值电压会发生骤增现象.这是因为同轴结构径比的变化使得不同阶数的微放电敏感区域发生相对偏移,而当这种偏移使得计算频点从高阶敏感区域进入低阶敏感区域时,相应频点处的微放电阈值电压就会突然上升.另外,当径比位于该范围的中间段时,同轴传输线的微放电阈值电压与功率会出现最小值,而且不同频点下对应于微放电阈值最小值的径比值也不相同.由此可见,同轴微波器件的设计优化必须考虑其在工程应用中的实际工作频率,并通过择优选取合适径比值来获得相对更高的微放电阈值.

图10 不同频点下同轴传输线微放电阈值电压与功率随径比的变化Fig.10.Effect of the radius ratio of coaxial transmission lines on multipactor threshold voltage and power for different frequency points.

4 讨 论

本文通过同时考虑单边碰撞和双边碰撞的统计理论稳态建模实现了同轴结构微放电的敏感区域计算以及器件结构与材料对微放电阈值的影响分析.事实上,考虑矩形波导中横向非均匀场分布的影响,这种改进稳态建模方法同样可以推广到矩形结构微放电研究中,由此解决现有稳态模型无法考虑单边碰撞而造成阈值精度低的问题.此外,改进后的稳态模型还可以进一步推广应用到其他非对称的微放电过程分析中,例如外加垂直静电场作用下平行平板结构以及介质填充平行平板与矩形波导中的微放电研究.

另外,上述研究还表明电子的快速振荡振幅会随着ηi的减小而逐渐增强,而缓慢漂移对整体电子轨迹的影响则会随之变弱.ηi<3.0参数范围内几乎可以忽略同轴结构中场分布的非均匀性,并用具有均匀场分布的平行平板结构来等效,因而两种结构微放电的敏感区域在左上方处应较为相似,但上述敏感区域图中却表现出非常显著的差异,而这主要是不精确的电子轨迹表达式所造成的.对于低SEY的镀膜材料而言,轨迹误差甚至会影响到右下方敏感区域处的阈值计算精度.然而同轴结构中无法推导得到精确的电子轨迹表达式,要解决近似电子轨迹表达式带来的计算误差问题,就必须在采用数值方法计算电子轨迹的基础上实现统计理论建模,而这也是未来统计理论发展与应用亟待解决的难题.

5 结 论

为实现精确有效的同轴传输线微放电阈值分析,本文采用由微扰法近似推导同轴结构的电子轨迹表达式,提出基于隐式关联性的联合概率密度函数构建方法,并在考虑单边与双边碰撞对微放电影响的情况下,推导同轴结构内、外导体处电子出射相位分布所满足的稳态积分方程组,由此实现了同轴结构微放电统计理论的稳态建模与分析.然后,采用该稳态模型分别计算银、铝、铜与阿洛丁等工程常用镀膜材料的同轴传输线微放电敏感区域.与欧空局的实验结果对比表明,近似电子轨迹表达式的误差在右下方的敏感区域(满足ηi<3条件)处可以忽略,因此稳态模型可以准确预测同轴传输线的微放电阈值.而具有低SEY分布的阿洛丁镀膜具有相对较小的敏感区域及较高的微放电阈值,是工程实际中实现微放电抑制的有效镀膜选择.另外与平行平板微放电相比,同轴结构微放电的敏感区域较为集中,尤其一阶与三阶敏感区域会发生明显的交叠,同时两种结构微放电阈值的相对大小在中间几阶敏感区域边界处交替变化.最后分析同轴结构径比对微放电阈值的影响规律发现,不同频率的同轴传输线微放电阈值功率在特定径比下会达到最小,实际的微波器件设计中须尽可能地避免采用该径比值,才能获得相对更高的微放电阈值功率.