试论数形结合在初中数学的必要性

（江西省吉安市峡江县水边中学 江西吉安 343000）

引言

课改的实施，改变了我国传统的应试教育，初中数学教学模式也变得较为灵活。特别是将多媒体技术引进后，在提高了教学效率的同时，也使学生更为透彻且直观的理解了数学的概念。在初中数学教学中，较为常见的方法之一就是数形结合，此种教学模式主要就是利用图形的形式使数学概念以及性质表现的更为直接，以方便应用。本文针对初中数学课程的部分教学内容进行分析，以探究数形结合在初中数学教学中的具体应用。

一、”数“与”形“之间的相互转换

我们常说，，数形之间可以相互转化，在特定的条件与要求下“数”可 以向 “形”转化，“形”可以向 “数”发生转化。”数“为”形“提供着理论依据，”形“为”数“提供着解决办法。数形结合就是我们经常说的，将复杂问题简单化，形象化，深入浅出，一时帮助学生更好的理解课本上的概念，二是通过数形之间的结合帮助学生认识数学与现实生活之间的关系。通过形象思维，提高学生的积极性 、主动性，提高了学生的素质能力。数形结合的实际是通过我们看起来比较直观的图形，线条，较为清晰的把抽象的内容表达出来，把复杂的数量关系表示出来，以及我们无法理解的概念，表达出来。另一种情况则是为了便于记忆，比如一些函数，通过图像我们就可以很清晰的看出他的性质，这样就解决了对于多个函数概念不清晰，容易搞混的问题了，继而提高解题效率，优化教学效果。要促进学生高效运用数形结合这一方法解决数学问题，教师必须指导学生体会并理解数形结合的思想，同时加强其在解题中的运用。

二、数形结合解决函数问题

对于一些稍微简单的函数还比较好，学生可以轻而易举的了解其性质，并且可以将图像与函数对应起来。图形我们可以理解为某一数学问题所对应的模型，这种模型辅助我们更直观的理解数学知识。但是许多数学问题都比较抽象，我们很难找打简单的模型来表达这个复杂的问题，所以理解一些问题就相对来说比较困难。数学实验可以变抽象教学为直观教学，帮助学生更好地学习。比如在学习什么是极大值，极小值，以及最大值，最小值，他们的区别是什么，对于这个问题借助图像来比较好理解，首先画一个抛物线，抛物线的顶点即为该函数的最大值，最大值的左边斜率是大于零的，左边函数是增加的，最大值的右边，曲线的斜率是小于零的，并且函数是不断减小的。如果只是学生自己进行看书所得到的知识点是片面的，只知道是这样子的，但是不知道为什么是这个样子的，只能掌握表面的知识。但是如果通过数形结合，学生会掌握一大部分，但是如果让学生自己通过画几何图形，学生在做中学、做中乐、乐中学”、学生在几何图形中观察、归纳、总结，验证假设，自己亲历探索原理、发现规律、解决问题的过程，达到学习数学质的飞跃，开拓了学生的思维空间，提高数学思维能力和解决问题的能力。

三、通过数形结合解决平行线角度的问题

图形问题在我们初中阶段还是占据了相当大的一部分，但是因为概念比较多，比较复杂，有的同学记不清，容易将一些概念进行混淆，于是我们可以借助数形结合的办法辅助学生理解概念。比如图1的问题。

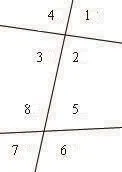
图1

同位角：∠1和∠5、∠2和∠6、∠3和∠7、∠4和∠8相对位置相同，称为“同位角”。同位角的形状似字母F。同位角相等两直线平行（可当定理使用）

内错角：∠2和∠8、∠3和∠5相互交错，且均在内部，称为“内错角”。内错角的形状似字母Z。内错角相等两直线平行（可当定理使用）

外错角：∠1和∠7、∠4和∠6相互交错，且均在外部，称为“外错角”。（有理论验证才可使用）

同旁内角：∠2和∠5、∠3和∠8在截线同旁，且均在内部，称为“同旁内角”。同旁内角的形状似字母U或门框形。同旁内角互补两直线平行（可当定理使用）

同旁外角：∠1和∠6、∠4和∠7在截线同旁，且均在外部，称为“同旁外角”。同旁外角的形状似希腊字母π。（有理论验证才可使用）

四、使用数轴解决数学问题

其实对于中学生而言，数轴是一个解决问题的好工具，数轴相较于其他工具而言啊，具有直观，清晰，明朗等优点。那么同学们必须要清楚的在数轴上进行表示出来其大小位置关系，并且能够一一对应，那么这样后面的问题就只有细心的发现了。数轴可以表示实数与非实数，绝对值等等，不仅仅可以表示一个数字，更可以表示一个方程，不等式之间的关系等等。如果能够熟练的使用方程，那么学生的学习将会轻松很多，逻辑思维能力，也会有待于提高，当然这一系列的过程离不开教师的辛苦引导。

结语

总而言之，基于初中学生的形象思维优于抽象思维的特点，数形结合教学方式，在初中，高中，乃至大学都是一个解题的好的方法，可以很大程度将书面语言转化成图形语言，形的重要性是不可忽视的。数与形的结合，有利于提高学生的探索欲望和求知欲，提高学生的自主学习能力。