数学数形结合思想在高中数学教学中的应用

（辽宁省大连市经济技术开发区得胜高级中学 辽宁大连 116635）

数形结合作为重要的数学思想，在高中数学学习中发挥着重要作用。通过数形结合可以将抽象数学问题具体化，让问题变的简单明了，降低教学难度，同时可以拓展学生解题思路，提高数学成绩。本文分析数形结合思想的内涵，结合高中数学特点，分析高中数学教学中数形结合思想的应用要点。

一、数形结合思想内涵分析

随着高中数学推行新课程标准，高考题型发生新的变化，出现如开放题、应用题及情景题，主要检测高中生数学创新思维能力、对数学思想方法的掌握，及综合运用数学知识的能力。分析历年高考试题发现，数学试卷中60%以上的试题含有数形结合思想，这意味着掌握数形结合法具有现实意义。

高中数学知识较为抽象，理解难度偏大，造成部分学生讨厌数学。但大部分数学知识都与几何图形存在联系，通过数形结合方法讲解知识点，可以降低数学知识理解难度。如绝对值讲解时，可以通过数轴让学生理解绝对值的含义，将抽象的理论知识具体化，加深记忆与理解；数形结合法本身就是一种解题方法，可以将抽象、繁琐的数学问题具体化、简单化，降低解题难度，提高解题效率。同时数形结合法可以帮助学生从不同角度解决问题，拓展出新的解题途径。总的来说，数形结合方法可以有效培养学生数学思维与解决数学问题的能力。

二、高中数学教学中数形结合的运用分析

1.数形结合解决集合问题

解决集合问题时，往往存在单纯求出各自集合答案，再进行合并计算，造成最终结构出现范围重叠，致使答案储蓄哦，也有可能出现无法计算的情况。引入数形结合思想，可以将这种复杂问题简单化，其中集合运算中Venn图最为常见。

如，一学校举行教学活动，此次教学活动共有50人参与，其中30人参加数学活动、26人参加物理活动，15人两种活动都参与。请问，这个班级中有多少同学既没参与数学也没参与物理活动？

一般解题思路：仅参加数学活动人数30-15＝15人，仅参加物理活动26-15＝11人，参加活动的人数＝15＋11＋15＝41人，什么也没参加的人数50-41＝9人。通过Venn图，可以直观观察到数量关系，简单的计算出最终结果。

2.数形结合解决函数问题

函数在高中数学中一向是复杂的存在，不但是一次函数的计算，更因为二次函数的复杂以及多变，不单单是解析法、列表法，更会直接出现图像法，会给计算带来更多的变化和复杂的计算量。尤其是在求定义域、最值和零点的时候，考虑的情况会更多，分情况讨论十分必要。这时候就必须要用数形结合的解题思路进行传统解题方式的突破。

例如在学习里程问题时，已知A、B两个地点的距离是4㎞，上午8点，甲从A地出发步行到B地，上午8点20，乙从B地出发骑自行车到A地，甲、乙两个人在离A地的距离与所用的时间之间的关系如图，根据图中的信息可以得知，乙到达A地的时间是多少？

通过题意可以知道，甲、乙两个人在离A地的距离与所用的时间关系图中所示，从原点出发的这条线是甲的图像，而另一条线是离A地的距离与所用时间是乙的图像。

此外，学生在解题过程中经常会遇到三角形的问题，但却没有办法与勾股定理相连结。数形结合是几何图形的纽带，如果用数形结合的方式去解决，学生就需要标注出三角形三边的边长，把边长与三角形有效的结合起来，使抽象的图形数字化，让学生在解题过程中能够更加直观，此时再用勾股定理的规律来判断就更加容易了。

3.数形结合对比函数值大小

高中数学学习中函数值大小比较较为常见，这也是高考常考题型之一，通过引入数形结合方法进行比较，可以快速得出直观答案，方便学生准确解决数学问题。

如：请判断0.3²、log20.3、20.3三个数的大小，并由小自大进行排序。

进行比较计算时可以将这三个数看成函数：y1＝x²、y2＝log2x、y3＝2x，假设x＝0.3时三个函数的对应值。随后在同一个坐标系上将三个函数的图像做出，如图2所示。

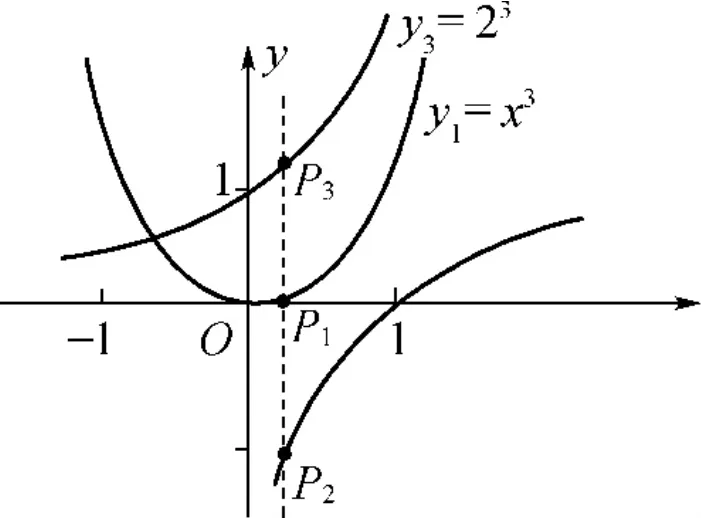
图2 y1＝x²、y2＝log2x、y3＝2x函数示意图

通过分析图像，可以很直观的看出，当x＝0.3时，三个函数分别对应P1、P2、P3三个点，进而获得20.3＞0.3²＞log20.3结果。

结语

总之，随着新课程改革深化，高中数学更加倾向考察学生灵活运用知识的能力。数形结合思想作为一种常见的数学方法，掌握其应用技巧，既可以降低数学教学难度，又可以提升学生解题效率，这就需要高中数学教学做好研究工作，促进教学质量提升。