主从机械手手爪设计与优化

丁彩红，张 中，赖 勇

（东华大学 机械工程学院，上海 201620）

1 引言

机械手爪在核电站内处于放射性物质的环境中，一旦发生故障，拆卸维修不仅使维修人员受到放射性污染，还会将污染源带到周边，造成二次污染。因此对机械手爪的设计提出了很高的可靠性要求。

美国，加拿大，德国都十分注重手爪的研制，分别研制了多种通用和专用机械手爪。如加拿大某公司与某大学合作研制成的欠驱动手爪SARAH[3]。该手爪结构简单，能获得类人手的抓举效果，但自由度少，对于不规则物体抓举缺少稳定性。美国斯坦福大学1983年研制成功Stanford/JPL多指灵巧手[3]。手指由12个直流伺服电机驱动关节元件，能够单独控制单根手指的运动，抓举适应性强，但控制复杂，设计开发难度较大。在国内，文献[1]设计了由电磁阀控制气缸运动，实现夹紧的搬运机械手爪。文献[4]于2013年研制了可对心抓取的平动机械手抓。手指之间的平动通过两端旋向不同的丝杠旋转完成张合动作，控制简单，自动对心，只适用于特定环境下圆柱形试管的抓举。

为此，针对现有机械手爪的优缺点，需要设计一种结构简单，控制方便，抓举可靠，适应性强的手钳。

2 手爪连杆设计

2.1 手爪设计要求

设计一款用于搬运核废料的机械手爪，要求能够抓举的尺寸不小于80mm，且能够抓举大于15kg的物体，设计安全系数不小于1.5。为了隔离辐射，人能够站在墙外隔墙操纵手爪。设计应考虑以下几个因素：（1）手爪的设计应有较大的载荷，保证抓举可靠。（2）手指应有足够的空间夹住物体，并对物体形状具有一定的适应性。（3）手爪应有足够的强度夹起物体。（4）在满足强度的要求下重量应尽可能小。

2.2 连杆设计方案

基于以上设计要求，采用钢丝绳带动拉杆传动，通过平行四边形机构实现平动，如图1所示。操作者通过手柄对手爪进行控制。操作者拉动手柄的连杆7，带动连杆8与收线轮9转动，收线轮9拉动钢丝绳10收线。钢丝绳穿过主手伸缩管、墙面和从手伸缩管与拉杆1的末端相连，拉杆1向上运动带动滑块2运动，滑块带动外臂3与内臂4以及手指5一起运动，实现抓举物体的功能，在手指5上固定橡胶，橡胶产生的变形对物体有一定的包络作用，增强机械手爪的适应性。连杆3与连杆4之间安装有弹簧以实现自动回中功能。

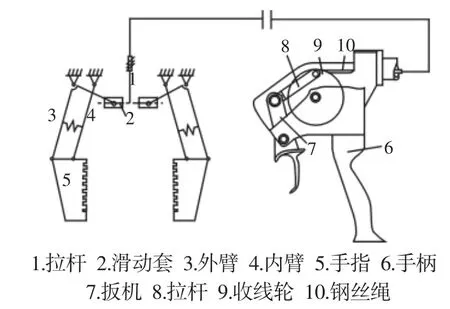
图1 手爪简图Fig.1 Gripper Diagram

由自由度的计算公式：

式中：n—运动机构的数目；Pl—低副的数目；Ph—高副的数目。

通过计算可得该装置的自由度为1，原动件的数目等于自由度的数目，可以确定唯一的运动。

3 最优力传递连杆尺寸及结构设计

连杆的力传动比是手爪设计的重要指标之一。机械手爪的连杆力传动比通过受力分析求得。

3.1 连杆受力分析

根据方案简图，选取滑块2、连杆3与手指5作为分析对象，忽略连杆所受的重力，其受力图，如图2所示。

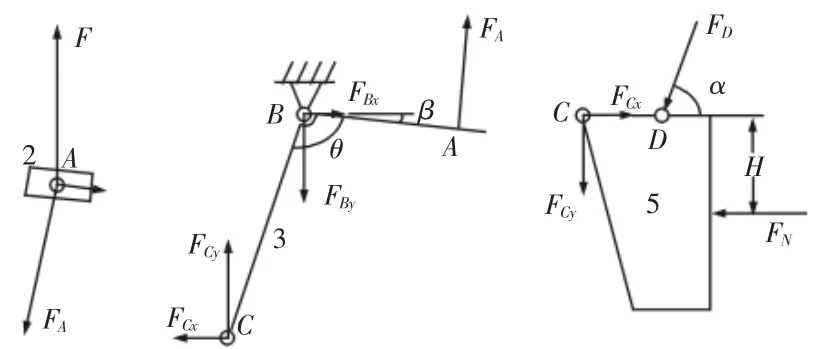
图2 手爪受力图Fig.2 Static Analysis of Gripper

由图2建立的受力图得到的静力方程为：

通过整理得到传动比i的表达式为：

根据平行四边形关系得到连杆夹角之间的关系为：

3.2 最优力传递连杆尺寸设计

3.2.1 设计变量

根据式（5）得到i只与 lAB、lBC、α、θ四个参数有关，在机构中lAB、lBC与α、θ互相独立，互不影响。因此先确定lAB、lBC的值。手爪最大张开距离为80mm，根据手爪最大张开距离和安装的空间限制选取lAB=50，lBC=40。将α、θ作为设计变量。

3.2.2 约束条件

连杆的C点到拉杆的垂直距离应在手爪的行程范围内。连杆点A到拉杆的垂直距离应在滑块的行程范围内。设滑块的最大行程为l，B点到连杆的垂直距离为d1，C点到手指端面的距离为d2，则α、θ的约束条件为：

l、d1、d2长度与 α、θ没有关联，因此可先确定 l、d1、d2的值。依据已确定的尺寸与空间限制确定l=4，d1=20，d2=37。经过计算得到α、θ的取值范围如下：

3.2.3 最优尺寸设计目标

连杆的传动比越大，输入力产生的输出力也越大。在手爪张合过程中连杆的位置不同，手爪传动比也不相等。选取手爪开闭过程中某一位置最小传动比作为手爪额定传动比，这一位置的最大抓举载荷作为机械手的额定载荷。并以额定传动比最大作为最优力传递目标。

3.2.4 Matlab最优力传递尺寸求解

由求得的公式用Matlab画出i关于α、θ关系图，如图3所示。

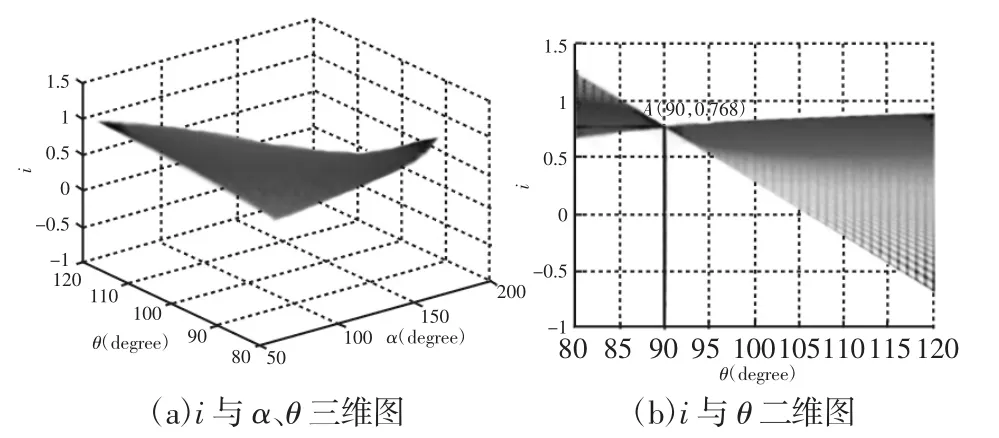
图3 i与α、θ关系图Fig.3 i，θCoordinate Diagram

在θ=90°时，手爪张合过程中传动比最小值取得最大，为0.768。因此选取θ=90°。得到的最终设计参数，如表1所示。

表1 手爪参数Tab.1 Gripper Parameter

根据载荷要求，选取直径为0.8mm的钢丝绳，其能提供的最大拉力为1000N，橡胶与金属的摩擦力为0.7。经过校核，该尺寸参数在1000N的输入力下能够对物体产生350N的提升力，满足所提出的设计要求。在Solidworks中完成手爪的三维建模，得到最终的模型。

4 连杆最大应力有限元求解

经典的材料力学只能解决简单结构力学问题，对于复杂的结构须借助有限元分析求解最大应力。

4.1 Workbench手钳有限元模型

4.1.1 建立物理模型

为了简化计算并得到质量更好的网格，在导入Work-bench模型前对Solidworks中的三维模型前处理，如去除小的圆角，小圆弧等。去除这些特征对模型的刚度影响很小，并不影响最后的分析结果。

4.1.2 接触约束

手爪与物体接触的面施加固定约束。在连杆与圆柱销相对转动的接触面添加不分离接触，允许其相对转动。在圆柱销与手爪过盈连接的地方施加绑定接触，限制所有自由度。

4.1.3 添加力载荷

钢丝绳传递主手施加的拉力并拉动拉杆。手爪的力载荷为手爪最大抓举力乘以安全系数。故在拉杆的端面施加1000N的拉力。

4.1.4 网格划分

采用Workbench自动划分网格，在计算机资源允许的情况下划分尽可能小的网格，保证求解的结果。划分四边形网格并指定网格大小为1mm，如图4（a）所示。

4.1.5 结果分析

根据图4（b）得到最大应力发生在弹簧安装位缺口处，其最大值为312MPa。在整体应力分布中，外支臂承受的应力分布最大。

4.2 Workbench外臂子模型分析

装备体中零件数量多，无法划分更多更小的网格。子模型分析将装配体中的一部分截取出来，并将装配体中的边界位移分析结果导入子模型边界，划分更小的网格，从而得到更精确的解，其他条件设置和装配体中的一样。

因在整体模型中最大应力发生在弹簧销的凹槽处，故切割靠近凹槽边界截取子模型。

图4 网格划分及结果Fig.4 Meshand Results

划分单元大小为0.3mm，如图4（c）所示。的网格得到最大应力值为359 MPa，如图4（d）所示。7075铝合金的许用应力值为455MPa，整个手爪的安全系数为1.28，低于许用安全系数1.5，故需对外臂结构进行优化设计。

5 外臂安全系数优化

在不改变原有的设计意图的情况下，运用尺寸优化法对其进行优化，使设计安全系数满足要求。

5.1 优化目标与约束条件

由有限元分析结果表明手爪外臂安装弹簧销的凹槽处安全系数小于设计值，故选取S最大作为优化目标。

式中：S-手爪安全系数；［σ］-材料屈服强度。

5.2 优化参数

凹槽的形状与尺寸参数P1，P2，P3有关，如图5所示。分别代表槽开口的长度，圆弧的直径，圆弧的深度。

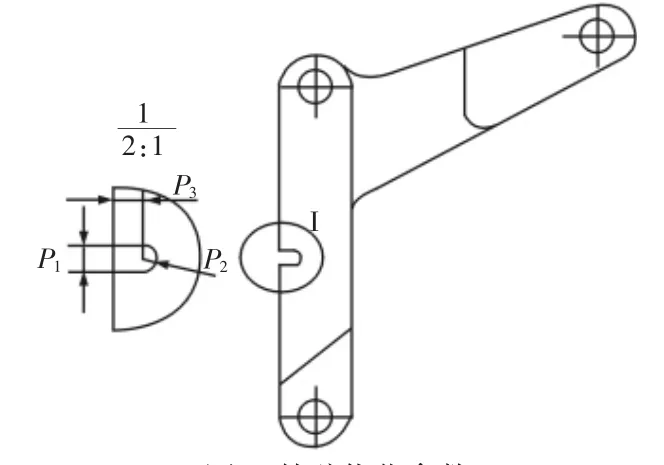
图5 外臂优化参数Fig.5 Outer Arm Optimization Parameters

5.3 约束条件

约束P1，P2，P3的主要因素是销的直径。销的直径不能太大或者太小。在原有的尺寸上下浮动：

同时应满足：

5.4 优化方法及结果分析

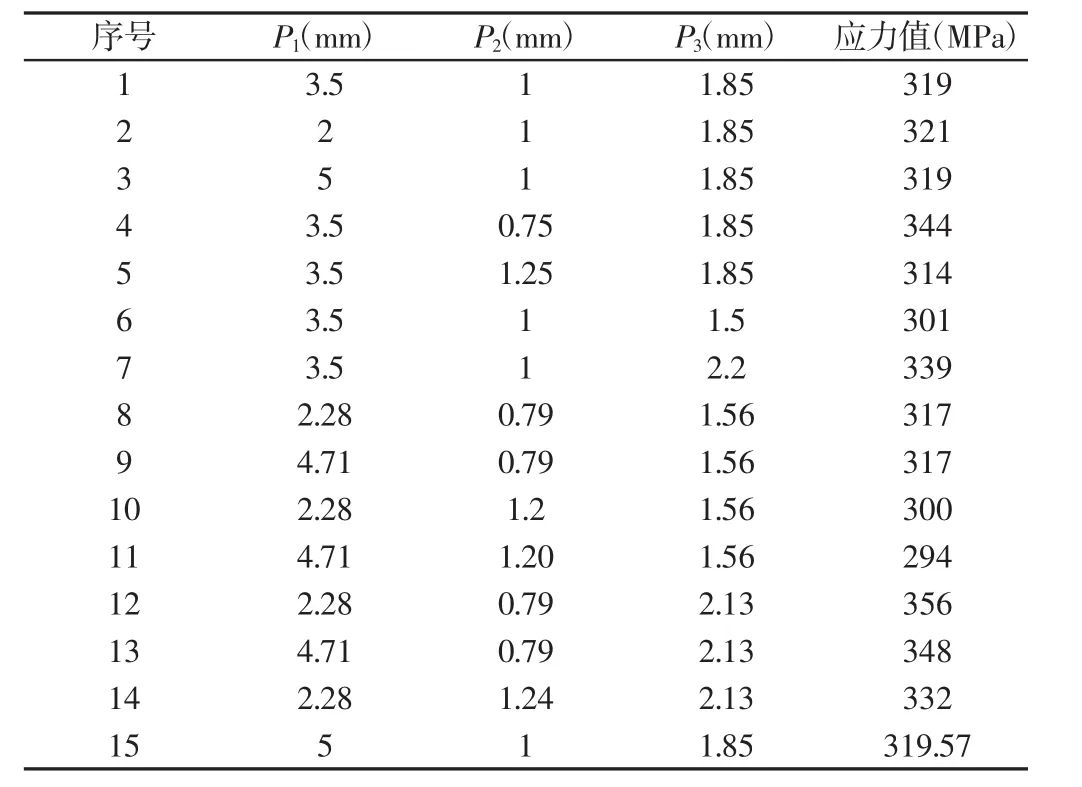
表2 设计参考点Tab.2 Design Point

在不改变原有的设计意图的情况下，对手爪进行尺寸优化。通过响应曲线法得到单个参数与优化目标的关系曲线，并得出最优尺寸。相对于DOE优化方法，响应曲面法能够有效地节约计算机资源，减少计算时间。在Solidworks建立优化变量并导入Workbench中，并将最大应力值作为优化目标。设置优化参数的上限和下限，Workbench自动生成设计参数点，求解并分析结果，如表2所示。根据生成的15组参数与对应的应力值Workbench运用统计学的方法，选取多项式模型拟合单个变量与结果之间的关系，如图6所示。响应曲线图中横坐标中的0表示设计参数的约束下限，横坐标中的1表示设计参数的约束上限。参数按比例从（0～1）由小变大。由图可得最大应力值与P1的变化无关，随P2的增大而减小，随P3的增大而增大，据此选择P1=2，P2=1.25，P3=1.5。优化前后结果，如表3所示。经过优化后的最大应力值减小了64MPa，如表3所示。相对于优化前提升了17.8%，满足了安全系数大于1.5的要求。

图6 参数响应曲线Fig.6 Parameters of the Response Curve

表3 优化前后对比Tab.3 Comparison Before and After Optimization

6 结论

结合上文提出以下结论：（1）结合国内外机械手爪的优缺点并针对设计要求，提出一种机械手爪的设计方案。（2）针对该方案，根据传动比确定连杆最优力传递性能，选取连杆长度与角度，并根据功能性与轻量化要求设计连杆的结构。（3）运用Workbench软件对手爪进行有限元分析，并得到手爪的薄弱环节，并运用Workbench中的响应曲线法找出优化尺寸与手爪最大应力之间的关系，确定优化尺寸参数。使手爪满足强度要求。（4）利用上述设计方法，设计出了尺寸合理，结构可靠的机械手爪，并缩短了设计时间，节省了设计费用。