不等径连续变截面圆管结构压降计算方法研究

姚利明，刘巨保，花明泽，刘玉喜

（1.东北石油大学 机械科学与工程学院，黑龙江 大庆 163000；2.大庆油田井下作业分公司 工程地质技术大队，黑龙江 大庆 163453）

1 引言

在石油管道及井下作业工具中，存在大量的圆管及连续变截面结构，准确计算其压降和水头损失不仅为输送管道设计、附件及工具选型提供理论依据，还为管道安全和高效运行提供技术支撑[1-2]。目前，国内外学者对圆管、缩径或扩径等变截面结构输送介质所产生的水头损失和压降已开展了大量的研究，文献[3-5]对突缩、突扩圆管进行了理论和实验研究，修正了摩阻系数；文献[6-8]人应用数值模拟和实验的方法，提出了速度水头的动能修正系数，给出了回流长度计算公式、计算了两相流变径管压力损失。文献[9]通过缩径、扩径结构验证了数值模拟的正确性，并确定缩径、扩径局部压降产生的流道有效长度，给出了缩扩结构、扩缩结构变径长小于临界长度的压降计算公式，及圆管连续变截面结构压降计算公式。这些研究成果为圆管、缩径或扩径变截面结构提供了可靠的压降计算公式，但对于截面尺寸不同的连续变截面结构压降计算，现有文献未给出明确结论和可行的计算公式。为此，通过理论分析和数值模拟相结合的方法，研究紊流状态下，不等径连续变截面圆管结构的压降计算方法，并回归出可靠的计算公式。

2 变截面圆管结构压降理论计算公式

2.1 缩径或扩径结构压降计算公式

在变截面圆管结构中，最常见的是缩径或扩径结构，如图1所示。在牛顿流体介质中，该结构已有成熟的压降计算公式[1-5]。

图1 圆管缩径或扩径结构示Fig.1 The Necking and Expanding Structure of Tube

对于缩径结构，如图1（a）所示。其压降计算公式为：

式中：Δps、Δpk—缩径和扩径压降，MPa；D、d—大径和小径直径，m；vD、vd—大径和小径截面平均流速，m/s；hjs、hjk—缩径和扩径水头损失，m；ρ—液体密度，kg/m3；g—重力加速度 m/s2；缩径、扩径局部压降产生的流道有效长度。

文献[9]通过对缩径、扩径结构的理论和数值模拟压降计算，验证了数值模拟的正确性，确定了缩径、扩径局部压降产生的流道有效长度，分别为0.25D和2.0D、0.0D和3.5D。

2.2 缩扩或扩缩结构压降计算公式

圆管缩扩和扩缩结构示意图，如图2所示。

图2 圆管缩扩和扩缩结构示意图Fig.2 The Necking-Expanding Structure and Expanding-Necking Structure of Tube

文献[9]通过对圆管缩扩和扩缩结构的流场数值模拟分析，提出了缩扩结构在变径长小于临界长度Ldcr=2.0D、扩缩结构变径长小于临界长度LDcr=3.75D的压降计算公式，如下：

缩扩结构压降计算公式为：

式中：Δpsk—缩扩结构压降；Kd—缩径结构压降影响系数；nd=Ld/d；当 0.04≤nd≤2，Kd按式（5）计算；当 nd≥2 时，Kd=1；Δpfd—缩径段沿程压降，缩径段直管长为Ld-2d。扩缩结构压降计算公式为：

式中：Δpks—扩缩结构压降；KD—扩径结构压降影响系数；nD=LD/D；当 0≤nD≤3.75，KD按式（6）计算；当 nD≥3.75 时，KD=1；ΔpfD—扩径段沿程压降，扩径段直管长为LD-2D。

2.3 连续变截面圆管结构压降计算公式

连续变截面圆管结构示意图，如图3所示。当图3中D1=D2=D3和d1=d2=d3时，文献[9]给出了连续变截面圆管结构压降计算公式：

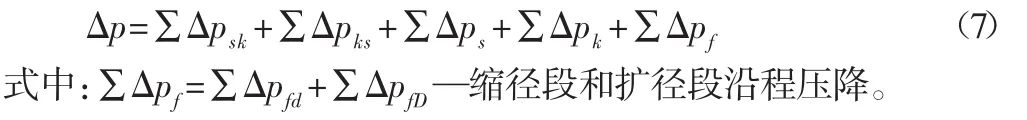
但式（7）不适用于 D1≠D2≠D3和 d1≠d2≠d3的情况。因此，拟采用理论分析与数值模拟结合的方法，推演出适用于D1≠D2≠D3和d1≠d2≠d3的连续变截面圆管压降计算公式。

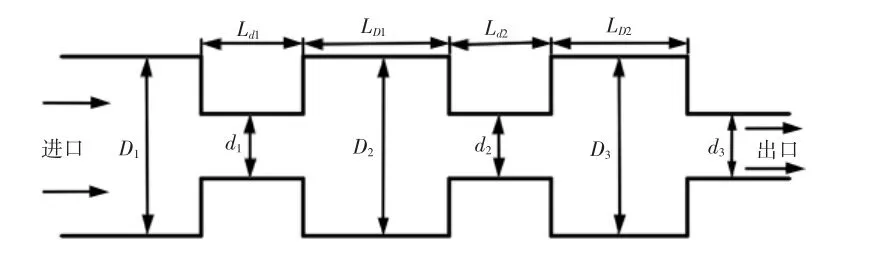
图3 连续变截面圆管结构示意图Fig.3 The Continuous Variable Cross-Section Tube Structure

3 进出口不等径缩扩和扩缩结构压降数值模拟与计算公式

3.1 进出口不等径缩扩和扩缩结构

当图2（a）所示圆管缩扩结构中D1≠D2时，构成了石油管道中普遍存在的进出口不等径缩扩结构，同理图2（b）所示圆管扩缩结构中d1≠d2时，便构成进出口不等径扩缩结构。前述研究结果适用于进出口等径的缩扩和扩缩结构，但是否适合于进出口不等径的缩扩和扩缩结构，有待于进一步研究验证。

3.2 进出口不等径缩扩和扩缩结构压降计算工况及数值模型

图2（a）所示的进出口不等径圆管缩扩结构取Ld为0.01D、0.1D、0.5D、2.0D 四种结构，当 D1＜D2时计算了 D1/D2为 0.4、0.6、0.8、1.0 四种结构，D1＞D2时计算了 D1/D2为 1.0、1.25、1.66、2.5 四种结构。2（b）所示的进出口不等径圆管扩缩结构取LD为0.1D、1.0D、2.0D、3.75D 四种结构，当 d1＜d2时计算了 d1/d2为 0.4、0.6、0.8、1.0 四种结构，d1＞d2时计算了 d1/d2为 1.0、1.0、1.25、1.66、2.5四种结构，流量均取5m3/min。

根据变截面圆管轴对称结构，建立其三维中心对称模型，采用非均匀化网格离散，并对壁面网格细化，要求单元的形状比率不超过8：1，倾斜的角度不超10°，缩扩结构网格模型如图4（a）所示。流态描述采用k-ε方程[10]。如图4（b）所示。模型处理为进口速度边界和出口压力边界，轴心线处理为对称边界。后面所涉及的模型网格划分及边界条件均采用上述方法处理。

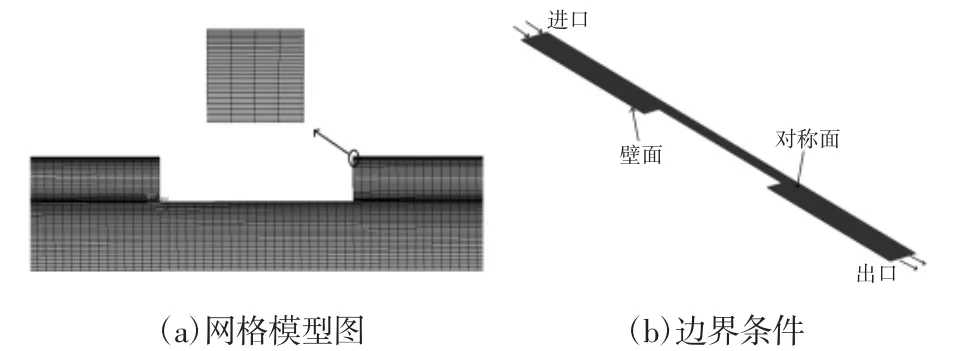
图4 缩扩结构数值模型及边界条件示意图Fig.4 The Numerical Model and Boundary Condition of Necking-Expanding Structure

3.3 计算结果与分析

进出口不等径缩扩结构的数值模拟和理论压降计算结果，如表1及式（3）所示。由表中数据可知，在计算的32种工况中，有7种工况相对误差在10%左右，其余25中工况相对误差均在5%左右，式（3）基本可应用于进出口不等径缩扩结构的压降计算。表2列出了进出口不等径扩缩结构的数值模拟和式（5）理论压降计算结果。由表中数据可知，式（5）与数值模拟计算结果相对误差在15%以上的占计算工况总数的六成以上，说明此式不适用于进出口不等径的扩缩结构压降计算。为此，需根据文献[9]研究得出的压降累加特性及变截面圆管能量损失原理，对式（5）修正，得通用扩缩结构压降计算公式：

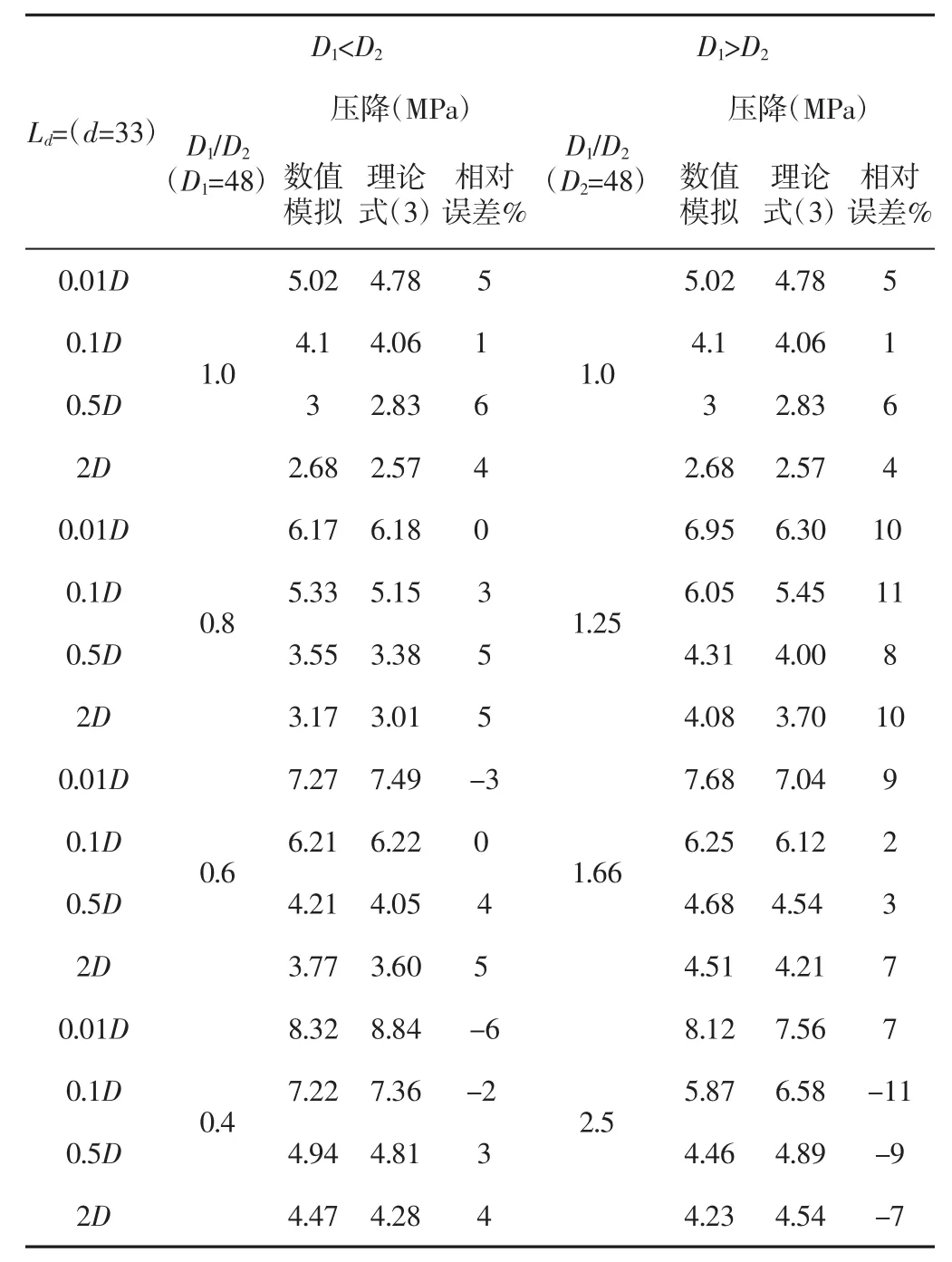
表1 进出口不等径缩扩结构压降计算结果Tab.1 The Pressure Drop Calculation Result of Unequal Diameter Inlet and Outlet Necking-Expanding Structure

将式（8）的计算结果一并列入表2中，由表2可见，计算的32种工况中，相对误差均在5%左右，最大误差不超过10%，因此该公式计算精度基本上能满足工程需要。另外，式（8）应用范围包括了进出口等径压降计算，故计算缩扩结构压降时，使用式（8）即可。

表2 不等径扩缩结构压降计算结果Tab.2 The Pressure Drop of Calculation Result of Unequal Expanding-Necking Structure

4 不等径连续变截面圆管结构压降计算

综合上述分析结果和变截面圆管结构压降的可叠加性，推广出圆管不等径连续变截面结构压降计算公式为：

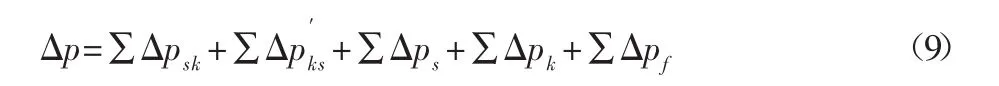
选取的不等径连续变截面圆管结构研究对象，如图3所示。结合图3分析可知，根据和长度不同，可将连续变截面圆管结构分为四种类型，而式（9）也可按照连续变截面圆管结构的不同类型化简为相应的计算公式，具体如下。

第一种：Ld≥Ldcr且LD≥LDcr，此时，算例可分为三个缩径、两个扩径和四段直管结构来计算压降，式（8）可化简为：

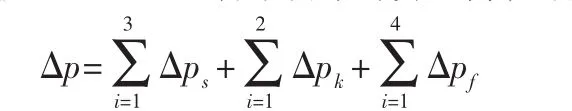
第二种：Ld≤Ldcr且LD≥LDcr，此时，算例可分为两个缩扩、一个缩径和两段直管结构来计算压降，式（8）可化简为：

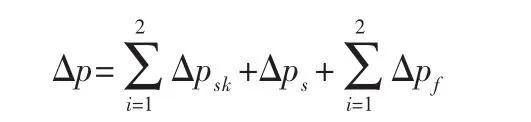
第三种：Ld≥Ldcr且LD≤LDcr，此时，算例可分为一个缩径、两个扩缩和两段直管结构来计算压降，式（8）可化简为：

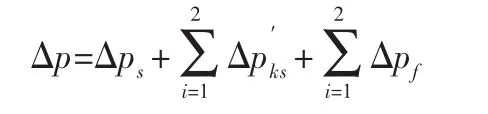
第四种：Ld≤Ldcr且 LD≤LDcr，此时，算例无法分解，式（9）无法应用。

为验证式（9）的可靠性，不防任选连续变截面结构参数，验证压降计算方法的准确性。圆管不等径连续变截面结构参数，如表3所示。计算流量取6m3/min，计算结果，如表4所示。

由表4可知，在第一至第三类结构中的共10种算例中，式（8）计算的变截面圆管结构压降结果均小于数值模拟结果，相对误差均在10%以内，这说明式（9）完全可以应用到前三种变截面圆管结构。但对于第四种结构（Ld≤Ldcr且LD≤LDcr），目前没有可行的理论计算公式。

表3 圆管不等径连续变截面结构参数Tab.3 Unequal Diameter Continuous Cross-Section Structure Parameter

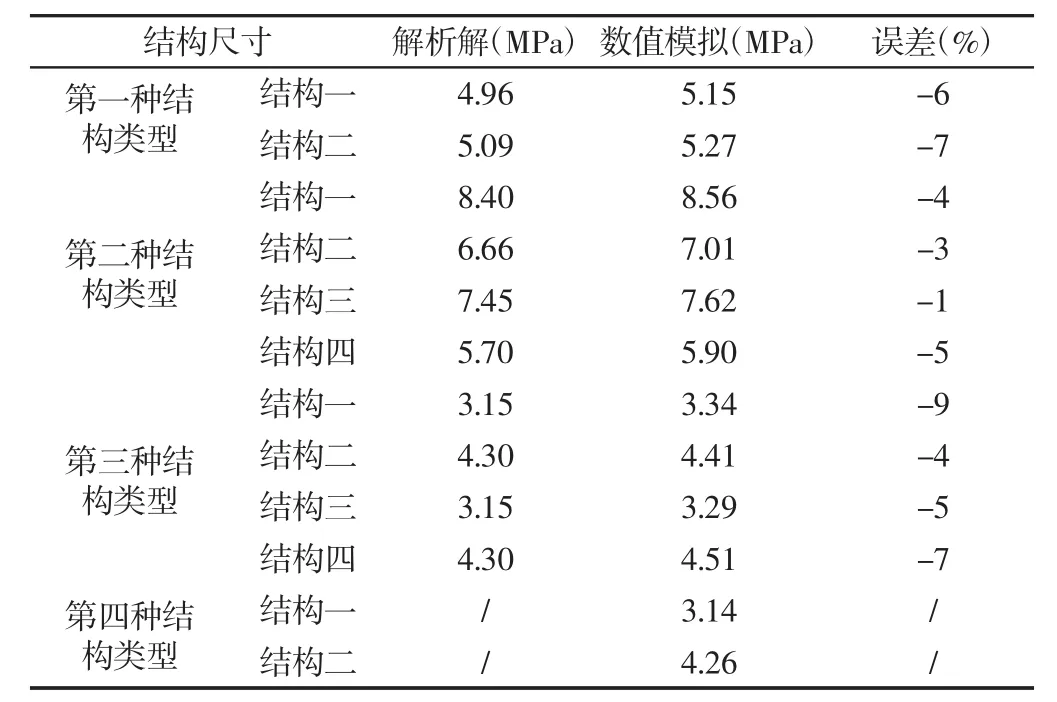
表4 不等径连续变截面结构计算结果Tab.4 Unequal Diameter Continuous Cross-Section Structure Calculation Result

5 结论

（1）通过对不同缩扩、扩缩变截面结构的流场数值模拟，得出进出口不等径的缩扩和扩缩结构压降计算公式及适用范围。

（2）根据管道沿程压降累加特性，建立了不等径连续变截面圆管结构压降计算方法，为相邻缩扩结构Ld与扩缩结构LD不同时小于临界长度的此类变截面圆管结构压降计算提供了理论计算公式。

（3）给出的连续变截面圆管结构压降计算公式仍具有局限性，如：相邻扩缩和缩扩结构的Ld与LD同时小于其临界值的连续缩扩结构无法使用，此类结构压降的理论计算公式，有待于进一步研究。