考虑Hoek-Brown准则和孔压效应隧道掌子面可靠度分析
张佳华,王卫军,张道兵,马宗宇
考虑Hoek-Brown准则和孔压效应隧道掌子面可靠度分析
张佳华1,王卫军1,张道兵1,马宗宇2
(1. 湖南科技大学 南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室, 煤矿安全开采技术湖南省重点实验室,湖南 湘潭 411201; 2. 湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201)
运用极限分析上限定理和可靠度理论构建隧道掌子面的可靠度模型,分析Hoek-Brown破坏准则和孔隙水对隧道掌子面可靠度的影响。研究结果表明,地质强度指标,扰动因子,孔隙水压力系数,水位线高度和岩体容重是影响隧道掌子面可靠度的主要因素。并且针对主要影响因素,给出3种不同安全等级下隧道掌子面维持稳定所需要的安全系数和支护力,为其支护设计提供理论依据和参考。
Hoek-Brown破坏准则;孔隙水;极限分析;可靠度
隧道开挖打破了掌子面前方围岩的原始平衡,继而产生变形,如果支护不及时或支护力不足会导致掌子面坍塌,这不仅给施工人员的生命带来极大的威胁,也给整个工程造成难以估量的损失。因此,确保掌子面稳定是隧道开挖的重点,对掌子面的稳定性进行可靠度分析具有重要的科研价值和工程意义[1−2]。近些年,许多国内外学者对隧道掌子面的稳定性问题进行研究,并且取得了一系列重要的成果。Subrin等[3]根据离心机的试验结果构建隧道掌子面的双对数螺旋曲线破坏模式,采用极限分析法得到不同破坏范围的围岩压力。Mollon等[4]采用“点对点”的方法构建隧道掌子面的破坏模式,该破坏模式形状极似双对数螺旋曲线,利用极限分析方法验证了破坏模式的合理性,并且求解了掌子面的极限支护压力。YANG等[5]针对隧道掌子面的坍塌破坏构建了速度场渐变的多块体破坏模式,采用极限分析法推导支护力的解析解,并且验证了结果的正确性,但是初始速度竖直向下的假定不太符合实际。杨峰等[6]认为隧道掌子面破坏时其速度发生突变是不严格的,于是构建由竖直方向渐变为水平方向的速度场,并且运用极限分析法得到掌子面坍塌时的围岩压力。但破坏模式比较复杂,不便于在实际工程中推广和应用。许敬叔等[7]根据二维对数螺旋曲线破坏模式,利用极限分析上限定理讨论土体参数对隧道掌子面围岩压力的影响。梁桥等[8]基于二维对数螺旋曲线破坏模式,采用极限分析上限法推导非均质土质隧道掌子面的围岩压力。杨子汉等[9]针对破碎软岩隧道,构建掌子面的二维多块体滑移破坏模式,并且通过极限分析上限法得到掌子面的坍塌压力以及潜在破坏面。上述研究运用极限分析上限定理确定隧道掌子面坍塌破坏时的围岩压力,但是并没有给出在安全等级下隧道掌子面维持稳定所需要的安全系数和支护力。因此,本文基于双对数螺旋曲线转动破坏模式,考虑孔隙水效应和Hoek-Brown破坏准则,采用极限分析上限定理和可靠度理论研究隧道掌子面稳定性的可靠度,为其支护设计提供理论指导和参考价值。
1 考虑孔隙水压效应的极限分析上限定理
孔隙水是影响岩土工程稳定性的重要因素,1955年Bishop提出确定孔隙水压力大小的方法,即孔隙水压力是岩土自重应力的一个分量,其表达式为:

式中:和u分别表示孔隙水压力及其系数;表示土体容重;表示在竖直方向上土中某点到地表的距离。
在岩土工程的稳定性分析中,孔隙水压力被分别视为内力和外力2种方法引入极限分析上限定理中进行研究。研究成果表明,当孔隙水压力被视为外力时,孔隙水压力使土体发生体应变做的功率和孔隙水压力在边界上做的功率等价于孔隙水压力被视为内力时渗透力和浮力做的功率,具体表达式如下所示[10−11]:



然而,将孔隙水压力当作外力时,物理意义更加明确,更容易让人接受,所以,后来很多学者都将孔隙水压力视为外力引入极限分析上限定理中。综上所述,孔隙水压力下的极限分析上限定理可表述为[12−13]:

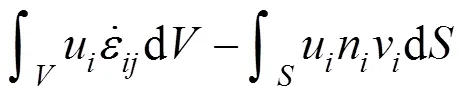

2 Hoek-Brown破坏准则
Hoek-Brown破坏准则是针对于岩体破坏的一个经验公式,为了在实际工程中得到应用,Hoek- Brown破坏准则经过5次较大的修改,最终表达式为[14−15]:

式中:1和3分别表示最大有效主应力和最小有效主应力;ci表示单轴抗压强度;b,和为无量纲参数,与岩体的特征有关,且有:

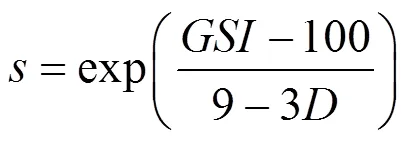

式中:表示岩体地质强度指标;m表示岩体常数;表示岩体扰动因子。针对实际工程,该参数可以参考文献[16]进行取值。
针对Hoek-Brown准则,YANG等提出“切线法”得到等效黏聚力和内摩擦角,如式(8)所示[17−18]。将式(8)代入极限分析上限定理中得到的解必定是真实值的一个上限解。


3 计算模型
隧道掌子面发生破坏时,前方岩体呈非均匀速度场,本文引用Subrin等[3]提出的双对数螺旋曲线破坏模式。如图1所示,为掌子面,高度为;和分别为2条对数螺旋曲线,且都以恒定角速度绕点旋转,其中长度为a,长度为b;另外,和与竖直线的夹角分别为1,2和3;T为掌子面支护力;为地下水位线到拱顶的高度,为孔隙水压力。

图1 隧道掌子面计算模型
在图1中,对数螺旋曲线和的表达式分别为:


根据图1中的几何关系可得:



4 计算过程
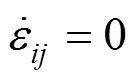
4.1 重力功率

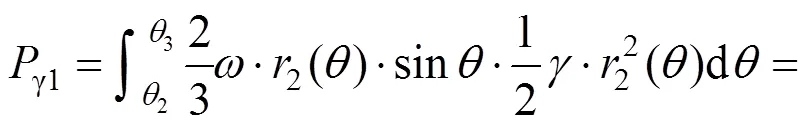
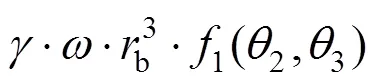




其中:
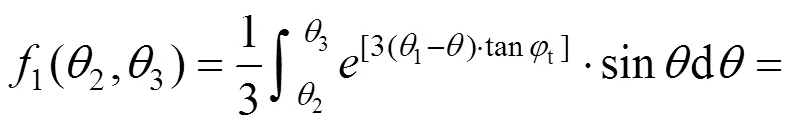



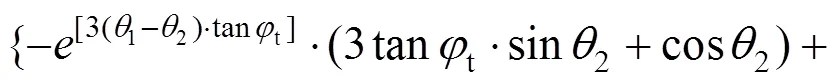
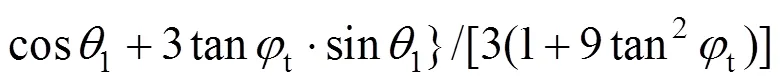
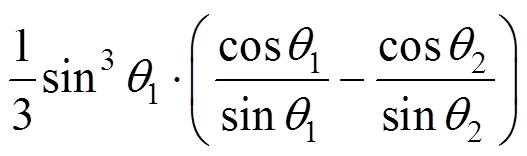
综上所述,岩体重力产生的总功率为:

4.2 孔隙水压力功率




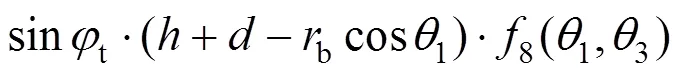
其中:
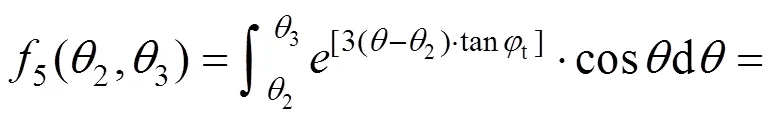

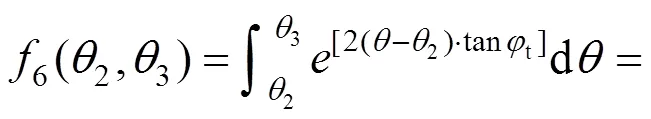




综上所述,孔隙水压力的总功率为:


4.3 支护力功率
在极限状态下,隧道掌子面的围岩压力等于其维持稳定所需要的支护力,可简化为均布荷载,记T,则支护力产生的功率为:


4.4 内能耗散率

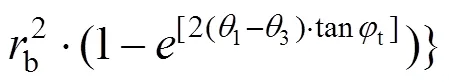
4.5 围岩压力与支护力
联立式(22),(29),(30)和(31),根据外功率与内能耗散率相等可求解隧道掌子面的围岩压力0,其表示为:

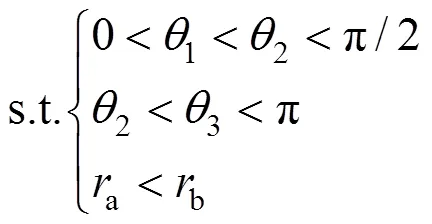
4.6 可靠度模型
若隧道掌子面支护设计的安全系数为s,则实际支护力T应为:

考虑岩体参数与荷载的随机性,则隧道掌子面的极限状态方程为:

要使隧道掌子面不发生破坏,则功能函数必须满足:

那么,隧道掌子面的可靠度模型为:

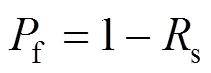

其中:s为可靠度;f为失效概率;为可靠指标;与()分别为随机变量组成向量与功能函数组成向量,表达式分别为:


5 对比验证


图2 本文与Senent等结果对比
6 可靠度分析
6.1 敏感性因子
随机变量的统计特性如表1所示,其他相应参数为:隧道直径=10 m,安全系数s=1。从图3中可得,扰动因子与孔隙水压力系数u对可靠度最敏感,水位线高度,岩体容重和地质强度指标对可靠度比较敏感,支护力T,岩体常数i和单轴抗压强度ci对可靠度不太敏感。
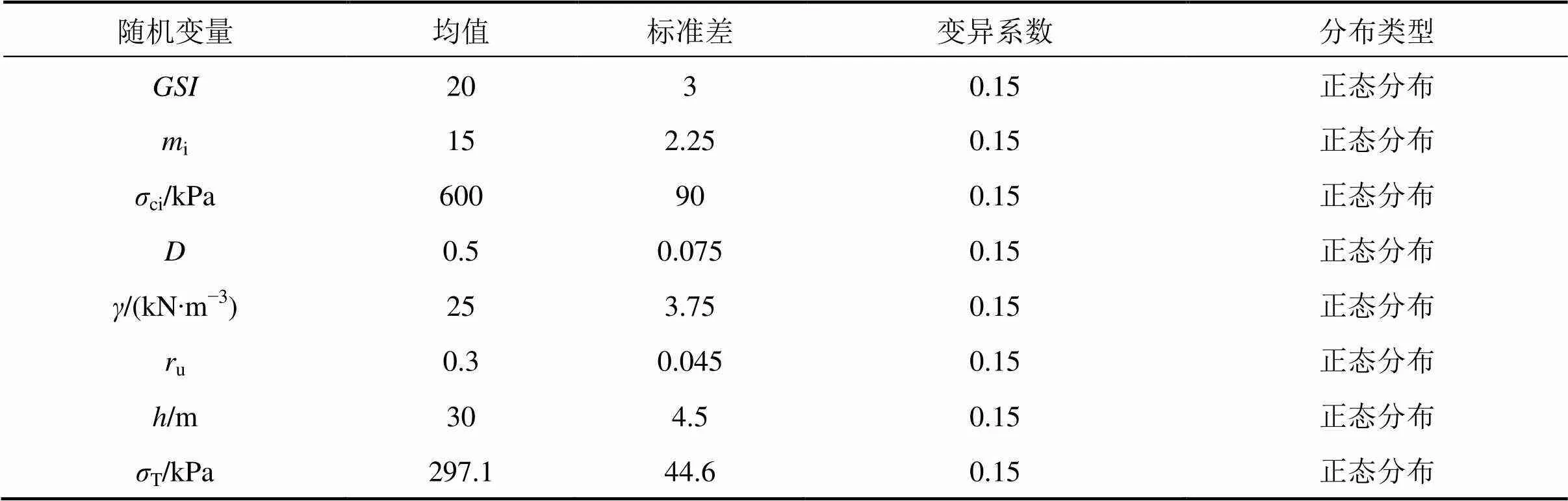
表1 随机变量的统计特性Ⅰ
6.2 安全系数与支护力
对随机变量进行敏感性分析可得,Hoek-Brown破坏准则参数中地质强度指标和扰动因子以及孔隙水压力系数u,水位线高度和岩体容重是影响隧道掌子面可靠度的主要因素。针对主要影响因素求解不同安全系数下隧道掌子面的失效概率。如图4所示,随着安全系数s的增大,失效概率f呈减小的趋势。对于Hoek-Brown破坏准则参数而言,扰动因子比地质强度指标的影响更大;对于孔隙水而言,水位线高度比孔隙水压力系数u的影响更大。针对图4,引入目标可靠指标[],可得到3种不同安全等级下隧道掌子面维持稳定所需要的最小安全系数与最小支护力,如表2所示,该计算结果可为隧道掌子面的支护设计提供理论依据和参考。
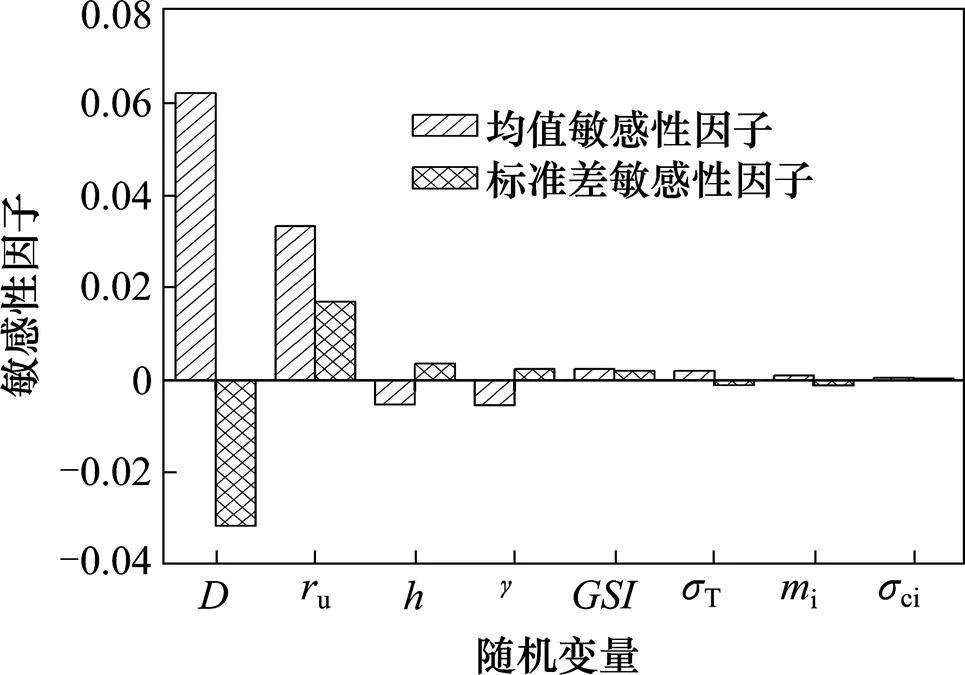
图3 各随机变量敏感性因子
表2 3种不同安全等级下隧道掌子面维持稳定所需要的最小安全系数与最小支护力
Table 2 Minimum safety factor and supporting pressure of tunnel face under 3 security levels

σ0/kPa[β] 3.23.74.2 FsminσTmin/kPaFsminσTmin/kPaFsminσTmin/kPa GSI10342.32.45838.62.88985.83.461 184.4 15316.02.47780.52.92922.73.481 099.7 20297.12.51745.72.97882.43.561 057.7 25282.32.52711.42.99844.13.561 005.0 D0256.12.55653.13.01770.93.63929.6 0.3276.62.52697.02.99827.03.61998.5 0.5297.12.49739.82.95876.43.601 069.6 0.7330.52.47816.32.90958.53.501 156.8 1484.62.591 255.13.041 473.23.721 802.7 ru0.1147.82.51371.02.97439.03.59530.6 0.2222.22.49553.32.93651.03.58795.5 0.3297.12.49739.82.93870.53.561057.7 0.4372.32.49927.02.931 090.83.561 325.4 0.5448.12.491 115.82.931 312.93.541 586.3

h/m10155.02.53392.22.99463.53.64564.2 20225.92.52569.32.96668.73.61815.5 30297.12.50742.82.95876.43.581 063.6 40368.42.47909.92.911 072.03.521 296.8 50439.82.431 068.72.851 253.43.441 512.9 γ/(kN∙m−3)17191.72.52483.12.95565.53.61692.0 19217.52.51545.92.95641.63.55772.1 21243.62.51611.42.95718.63.54862.3 23270.22.50675.52.93791.73.54956.5 25297.12.50742.82.93870.53.521 045.8
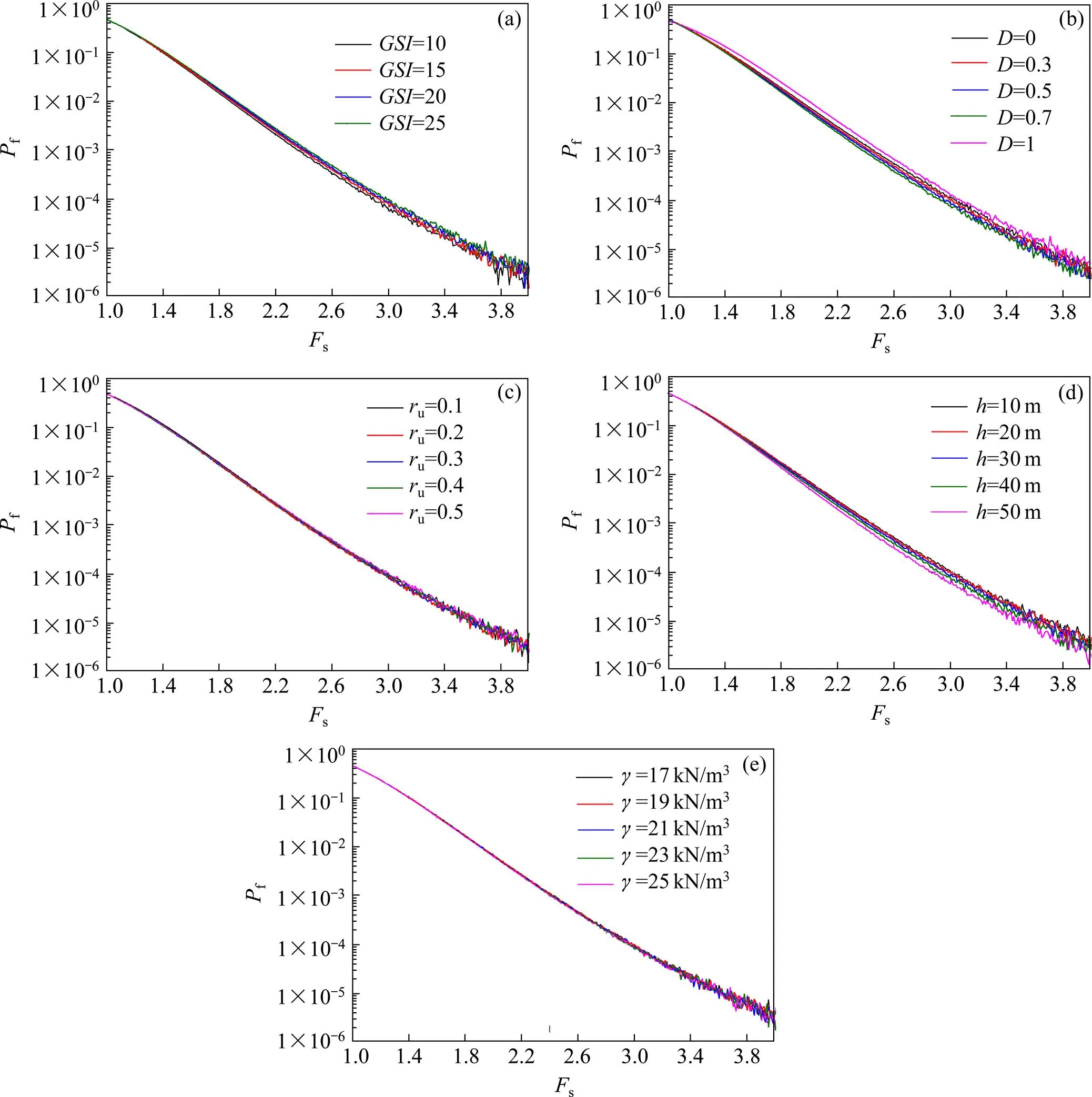
(a) 地质强度指标;(b) 扰动因子;(c) 孔隙水压力系数;(d) 水位线高度;(e) 岩体容重
7 结论
1) 基于Hoek-Brown破坏准则,采用极限分析上限定理推导孔隙水作用下隧道掌子面围岩压力的解析解。引入安全系数,根据围岩压力与支护力构建的极限状态方程建立了隧道掌子面的可靠度模型。
2) 通过敏感性分析可知,地质强度指标,扰动因子,孔隙水压力系数u,水位线高度和岩体容重是影响隧道掌子面可靠度的主要因素。对于Hoek-Brown破坏准则参数而言,扰动因子比地质强度指标的影响更大;对于孔隙水而言,水位线高度比孔隙水压力系数u的影响更大。因此,在围岩较差、扰动较大或孔隙水较丰富区段,应加强掌子面的预支护措施以及防排水措施,并且及时进行监控量测,以防止掌子面发生涌水突泥及坍塌事故。
[1] 张箭, 杨峰, 刘志, 等. 浅覆盾构隧道开挖面挤出刚性锥体破坏模式极限分析[J]. 岩土工程学报, 2014, 36(7): 1344−1349. ZHANG Jian, YANG Feng, LIU Zhi, et al. Three-dimensional limit analysis of blow-out failure modes of shallow shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1344−1349.
[2] Senent S, Mollon G, Jimenez R. Tunnel face stability in heavily fractured rock masses that follow the Hoek-Brown failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(1): 440−451.
[3] Subrin D, Wong H. Tunnel face stability in frictional material: a new 3D failure mechanism[J]. Comptes Rendus Mecanique, 2002, 330(7): 513−519.
[4] Mollon G, Dias D, Soubra A H. Rotational failure mechanisms for the face stability analysi of tunnels driven by a pressurized shield[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1363−1388.
[5] YANG Yuyou, LI Hongan. Failure mechanism of large-diameter shield tunnels and its effects on ground surface settlements[J]. Journal of Central South University, 2012, 19(10): 2958−2965.
[6] 杨峰, 阳军生, 赵炼恒. 浅埋隧道工作面破坏模式与支护反力研究[J]. 岩土工程学报, 2010, 32(2): 279−284. YANG Feng, YANG Junsheng, ZHAO Lianheng. Collapse mechanism and support pressure for shallow tunnel face[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 279−284.
[7] 许敬叔, 潘秋景. 盾构隧道开挖面支护力上限分析[J]. 铁道科学与工程学报, 2014, 11(4): 80−84. XU Jingshu, PAN Qiujing. Upper bound analysis of supporting pressure for shield tunnel faces[J]. Journal of Railway Science and Engineering, 2014, 11(4): 80−84.
[8] 梁桥, 杨小礼, 张佳华, 等. 非均质土体中盾构隧道开挖面支护力上限分析[J]. 岩土力学, 2016, 37(9): 2585− 2592. LIANG Qiao, YANG Xiaoli, ZHANG Jiahua, et al. Upper bound analysis for supporting pressure of shield tunnel in heterogeneous soil[J]. Rock and Soil Mechanics, 2016, 37(9): 2585−2592.
[9] 杨子汉, 杨小礼, 张佳华, 等. 不同饱和度下破碎软岩隧道掌子面破坏范围上限分析[J]. 中南大学学报(自然科学版), 2015, 46(6): 2267−2273. YANG Zihan, YANG Xiaoli, ZHANG Jiahua, et al. Upper bound analysis of collapsing area of tunnel face in broken soft rocks under different saturations[J]. Journal of Central South University (Science and Technology), 2015, 46(6): 2267−2273.
[10] Michalowski R L, Nadukuru S S. Three-dimensional limit analysis of slopes with pore pressure[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(9): 1604−1610.
[11] PAN Q J, Dias D. The effect of pore water pressure on tunnel face stability[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(15): 2123−2136.
[12] CHEN W F. Limit analysis and soil plasticity[M]. Florida: J. Ross Publishing, Inc, 2007.
[13] Shin J H. Analytical and combined numerical methods evaluating pore water pressure on tunnels[J]. Géotechnique, 2010, 60(2): 141−145.
[14] 许渊, 李亮, 邹金锋, 等. 考虑轴向力和渗透力时圆形隧道广义Hoek-Brown解[J]. 岩土力学, 2015, 36(10): 2837−2846. XU Yuan, LI Liang, ZOU Jinfeng, et al. Generalized Hoek-Brown solution of circular tunnel considering effects of axial stress and seepage force[J]. Rock and Soil Mechanics, 2015, 36(10): 2837−2846.
[15] 李硕标, 薛亚东. Hoek-Brown准则改进及应用[J]. 岩石力学与工程学报, 2016, 35(增1): 2732−2738. LI Shuobiao, XUE Yadong. Modification of Hoek-Brown criterion and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Suppl 1): 2732− 2738.
[16] Hoek E, Brown E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165−1186.
[17] YANG Xiaoli, YIN Jianhua. Slope equivalent Mohr- Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion[J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505−511.
[18] YANG Xiaoli, YANG Zihan, LI Yongxin, et al. Upper bound solution for supporting pressure acting on shallow tunnel based on modified tangential technique[J]. Journal of Central South University, 2013, 20(12): 3676−3682.
(编辑 阳丽霞)
Reliability analysis of tunnel face considering the effect of pore water pressure and Hoek-Brown failure criterion
ZHANG Jiahua1, WANG Weijun1, ZHANG Daobing1, MA Zongyu2
(1. Work Safety Key Lab on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines, Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China; 2. School of Resource Environment and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)
Reliability model of tunnel face was built based on the upper bound theorem of limit analysis and the reliability theory. The effect of pore water and parameters of Hoek-Brown failure criterion on the reliability of tunnel face was discussed. The results show that, geological strength index, disturbance factor, coefficient of pore water pressure, water height and unit weight of rock have significant influence to the reliability of tunnel face. In addition, safety factor and corresponding supporting pressure of tunnel face was presented under three security levels, which can provide theoretical basis and reference for the supporting design of tunnel face.
Hoek-Brown failure criterion; pore water; limit analysis; reliability
10.19713/j.cnki.43−1423/u.2018.12.021
TU43
A
1672 − 7029(2018)12 − 3173 − 08
2017−10−23
国家自然科学基金资助项目(51804113,51674115);湖南科技大学博士启动基金资助项目(E51768);湖南科技大学博士后科研基金资助项目(E61610);南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室开放基金资助项目(E21734)
张佳华(1983−),男,湖北天门人,讲师,博士,从事隧道与地下工程方面研究;E−mail:1010090@hnust.edu.cn

