铁路桥梁浅基础设计变量的不确定性分析

张威振



铁路桥梁浅基础设计变量的不确定性分析

张威振

(湖南中大设计院有限公司，湖南 长沙 410075)

设计变量不确定性的计算分析是修订基于可靠性理论设计规范的基础工作。对铁路桥梁浅基础采用以可靠性理论为基础的概率极限状态设计方法进行研究，将设计中各种设计变量的不确定性进行了归纳、整理。在此基础上，讨论荷载效应和地基土极限承载力的不确定性，确定永久作用和可变作用中几种主要荷载的无量纲化系数的均值、均方差和变异系数，并根据有关资料和可靠性原理推导地基土极限状态条件下的宽、深修正系数和地基土抗力变异系数的计算表达式。研究成果可为可靠性理论规范的改进和修订提供参考和借鉴。

浅基础；设计变量；不确定性；可靠性；变异系数

传统的岩土工程分析方法为定值分析方法，其中一个重要的参照指标就是安全系数[1]。而规范中给出的安全系数都是结合一定的工程经验总结得到，没有太多的理论指导，在适用范围上具有一定的局限性[2]。针对传统方法的缺陷，一种新的分析方法—可靠度分析法应运而生。李亚军等[3]采用响应面法分析研究岩土工程中的可靠度问题。WANG[4]提出了一种基于直接蒙特卡洛模拟的扩展可靠度设计方法。LI等[5]在岩土工程分析中引入了随机理论，将土体剖面视为一个空间二维随机场。工程结构的可靠性涵盖了安全性、适用性和耐久性。工程结构可靠是指在规定的时间内，在规定的条件下，其所预定的安全性、适用性和耐久性均得到保证，而工程结构的可靠度是指完成预定功能的概率，是工程结构可靠性的概率[6]。在建筑结构中已经采用概率论为基础、通过分项系数表达的极限状态设计方法，而岩土工程中的可靠性研究和设计理论落后于结构的发展[7]。岩土体是岩土工程中所涉及的主要材料之一，其主要特点是各向异性，其性质随着位置和方向的改变而改变[8]。土性参数的变异特性主要来自2个方面的原因：1) 土本身固有的空间不均质性；2) 取样、试验以及确定参数过程中包含的不确定性。在进行工程结构设计时往往会进行简化，假设岩土体的参数在一定区域内的同类土中是不发生变化的[9]。为了加强整个工程的安全性，我们应通过对勘察、设计、施工、监测等整个系统的各个部分的可靠度进行控制[10]。建(构)筑物总是通过基础将荷载传递到岩土体中去，所以基础的安全储备将直接影响上部结构的安全程度。本文将以铁路桥梁浅基础为对象进行研究。作用荷载和地基抗力的不确定性是浅基础承载能力设计变量不确定性的主要内容，这2个因素在工程设计时具有举足轻重的影响，故需要对其进行分析。通过对桥梁的下部结构即墩台基础的各种设计变量不确定性进行分析研究，为可靠性理论规范的修订提供参考。

1 浅基础设计变量

对于铁路桥涵浅基础承载能力可靠性分析的极限状态方程[11]可表述为：

=–(1)

式中：为极限荷载作用下基底压应力，是浅基础各种作用荷载(组合)的函数；为地基土抗力，即地基土极限承载力，为地基土强度、基础大小和埋深等设计变量的函数。

在极限荷载作用下，基底接触应力不再为线性分布，如何计算应做进一步研究。同样，现行桥规仅给出地基土的容许承载力[]计算模式，地基土极限承载力的计算模式也应研究。

根据式(1)，浅基础承载能力设计变量的不确定性分析，主要是荷载效应和地基土极限抗力的不确定性分析。但对于铁路桥梁浅基础，作用荷载的种类和组合比较多，荷载效应的不确定性分析按荷载的主要类型来分析。地基土极限抗力的不确定性计算中，由于岩土的复杂性，比一般结构抗力的不确定性计算要复杂得多，下面分别进行研究。

2 作用荷载的不确定性计算

铁路桥梁设计中的作用可分为永久作用、可变作用和偶然作用[12]，在浅基础承载力设计中，偶然作用一般不控制设计，因此本文对设计中的常遇作用即永久作用和可变作用的不确定性进行计算[13]。

2.1 永久作用

永久作用指的是对桥梁起经常性的作用，其作用点固定不变，也称为恒载。在铁路桥涵中，它主要指的是梁跨结构自重、桥面附加设施的荷载、桥墩及其基础的自重等。

2.1.1 桥面附加设施的荷载1

这部分荷载主要指上部结构中，除了梁体自重以外的荷载，包括人行道板、道碴和线路设备、栏杆及托架等。根据标准设计，桥面轨枕为混凝土枕时，对于直线梁，取均布荷载1=39.2 kN/m；对于曲线梁，取均布荷载1=48.1 kN/m。

根据上部结构的统计资料，N1的无量纲化系数(实际值与设计值之比，以下同)的均值为1.320 5，均方差0.089 9，变异系数为0.068 1。1或1的无量纲化系数服从正态分布。

2.1.2 梁跨自重2

一般采用标准设计的梁，由于梁体自重通过支座传递到墩顶，对于等跨桥，它等于单跨的每孔梁重，对于不等跨桥，则为两孔梁自重之和的一半。

统计资料表明，钢筋混凝土及预应力混凝土梁体自重2的无量纲化均值为1.020 2，均方差为0.021 9，变异系数为0.021 5。钢结构梁体自重2的无量纲化均值为1.019 0，变异系数为0.011 1。2或2的无量纲化系数服从正态分布。

2.1.3 桥墩及其基础(下部结构)自重3

这部分的自重应根据具体的设计而定，即根据下部结构的各自体积乘以相应容重而得的。以圆形桥墩为例，下部结构如采用同一材料，其变异性计算如下。

下部结构的体积为托盘、顶帽、墩身和基础的体积之和，其重量为：

3=×(2)

变异系数为：

通常视混凝土的容重为常量，3的变异性主要来自下部结构的体积V的变异。

例：设为圆形桥墩的上半径，墩高为，墩身坡度为，则墩底半径为+2/，又设基础(方形)的边长为，基础埋深为1，有

墩身体积

基础体积

4=21

并记托盘、顶帽的体积为5。于是下部结构的体积为

墩身坡度为常量，的变异性是由于下部结构的尺寸(，，和1等)的变异性引起的。由于长、宽、高尺寸的变异性较小，通常可认为它们的变异系数相等，均记为δ，则结合统计分析中的误差传递公式可得

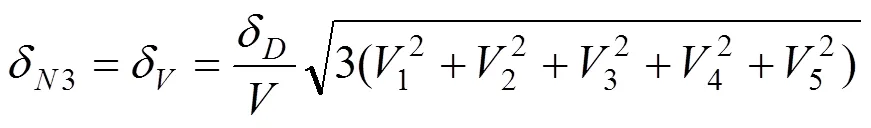
根据国内外资料，各尺寸的无量纲化(实际值与设计值之比)的均值k=1.01，δ=0.07，其中包括尺寸及位置偏移影响的变异性。

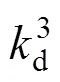
2.1.4 恒载(永久作用)的综合变异系数

上述恒载均服从同一分布(即正态分布)，根据统计理论，作用在基底上的总恒载=1+2+3也服从正态分布，总恒载的均值和变异系数可利用统计理论中的误差传递公式得到

实例计算：取标准图肆标桥4034的标准设计为例，其统计参数的计算如下：已知跨度为24+24米的简支梁桥，墩身高度为=22 m，墩身坡度为65.5:1(即=65.5)，墩顶直径为300 cm，墩底直径为368 cm，方形基底的边长为748 cm，基础埋深为3 m，则

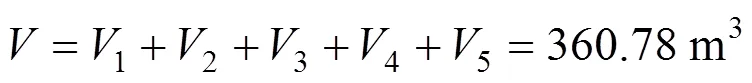
对于其他形式的桥墩如矩形桥墩、圆端形桥墩等，同样地进行其恒载的不确定性计算。

2.2 可变作用

可变荷载分为基本可变荷载和其他可变荷载。基本可变荷载包括列车的活载及动力效应、列车离心力、列车摇摆力以及列车活载产生的土压力；其他可变荷载则包括列车制动力或牵引力，风荷载，流水压力和冰压力等。

2.2.1 列车活载

对于铁路桥梁基础的设计，一般不考虑列车活载冲击力的作用，列车活载指的是列车静活载，规范规定列车静活载的加载图式为“中—活载”。浅基础承载力最不利的荷载一般为“双孔重载(低水位)”，根据统计资料，当桥跨>4 m时，列车静活载在基准期最大值的无量纲化均值为0.961 9，均方差为0.037 1，变异系数为0.038 6，且服从正态分布。

浅基础设计中的活载的均值和变异系数计算如下：

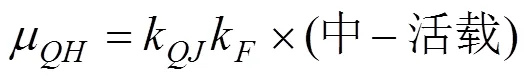
式中：k和δ为静活载的无量纲化均值和变异系数分别取0.961 86和0.038 6；k和δ为活载的超载系数的均值和变异系数，分别取1.000和0.013 0；(中—活载)为按照“中—活载”的加载图式求得最大支座反力(静活载)。

实例计算：对于标准图中24+24 m的简支梁，按照影响线加载图式，求得最大支座反力(静活载)为2 330.2 kN，则活载的统计参数为

2.2.2 列车离心力F

列车离心力F等于列车竖向静活载乘以离心力率C。离心力率C与线路设计行车速度及线路曲线半径有关，为一确定性系数，因此列车离心力F的变异性与列车竖向静活载的变异性有关，并具有相同的变异系数及分布。

2.2.3 列车横向摇摆力F

对于曲线桥应同时计算列车离心力与列车横向摇摆力，其作用方向相同。据上部结构的统计资料，列车横向摇摆力F的无量纲化系数(实际值与设计值之比，以下同)的均值为1.024，变异系数为0.322 3。列车横向摇摆力F或无量纲化系数可假定服从正态分布。

2.2.4 列车制动力或牵引力F

在浅基础的设计中，桥墩台的列车制动力为计算长度内列车竖向静活载的10%计，牵引力按加载长度等于或小于30 m内列车竖向静活载的15%计算。据上部结构的统计资料，列车制动力或牵引力F的无量纲化系数(实际值与设计值之比，以下同)的均值对于钢支座为1.00，变异系数为0.210。列车制动力或牵引力F服从正态分布。

2.2.5 风力

据上部结构的统计资料，风力服从极值I型分布。根据建工部门及林业部门的统计结果，风力的变异系数为0.35~0.47。

2.2.6 列车活载产生的土压力F,cp

这部分土压力的大小与静活载大小及土体的容重和内摩擦角有关。根据收集的资料，内摩擦角′的变异系数为0.10~0.15，容重的变异系数为0.04~ 0.10，由此得到土压力的变异系数为0.10~0.20。

2.2.7 流水压力F及冰压力F

目前缺乏这部分统计资料，有待于收集资料作进一步统计分析。

表1 铁路桥梁结构永久荷载及可变荷载的均值与标准值比值、变异系数和概率分布类型

Table 1 Ratio of mean to standard value, coefficient of variation and probability distribution type of permanent load and variable load of railway bridge structure

荷载分类荷载名称均值μ变异系数δ概率分布类型 桥跨自重钢筋混凝土及预应力混凝土结构N21.020 2N2K0.021 5正态分布 钢结构N21.019 0N2K0.011 1正态分布 附加恒载道碴桥面及线路结构自重N11.320 5N1K0.068 1正态分布 人行道明桥面自重N41.000N4K0.044 3正态分布 下部结构自重N31.030 3N3K正态分布 可变作用静活载(桥跨L>4 m)Q0.961 6NK0.038 6正态分布 列车离心力Fc0.961 6NCK0.038 6正态分布 列车横向摇摆力Fts1.024FtsK0.322 3正态分布

列车制动力或牵引力Fb1.00FbK0.210正态分布 风力W0.35值I型分布 列车活载产生的土压力Fq,cp0.10~0.20 流水压力Fwd及冰压力Fic———

注：下标表示标准值；在计算基础所受的可变作用时不考虑活载的冲击力

3 地基抗力的不确定性分析

现行桥规中，地基土的容许承载力采用地基土的基本承载力加宽深修正的形式来表示[14]。由于容许状态与极限状态的工作条件不一样，严格而言地基土的极限承载力不应采用和地基土的容许承载力类似的计算模式。考虑到规范修改的时间紧迫，其主要目的是对现行桥规作可靠度校核，且该计算模式为铁路设计人员所熟悉，铁路地基基础可靠性理论规范中推荐，地基土极限承载力计算表达式采用“极限承载力基本值加宽深修正值”的模式，如式(8)所示：

式中：为地基极限承载力计算值，kPa；0为地基极限承载力基本值，kPa，见文献[14]提出的研究报告和表2；1和2为地基极限承载力的宽深修正系数，由持力层确定，见表3，其确定方法参见文献[14]。

其他符号的意义与现行规范相同。

根据实测资料统计分析，在转换到极限状态时，地基土极限承载力基本值0比0对于不同类别的土有不同的提高，提高幅度大致在2左右，见表2。不同土的极限承载力基本值0已由“地基承载力标准值专题组”提出，本研究直接采用。

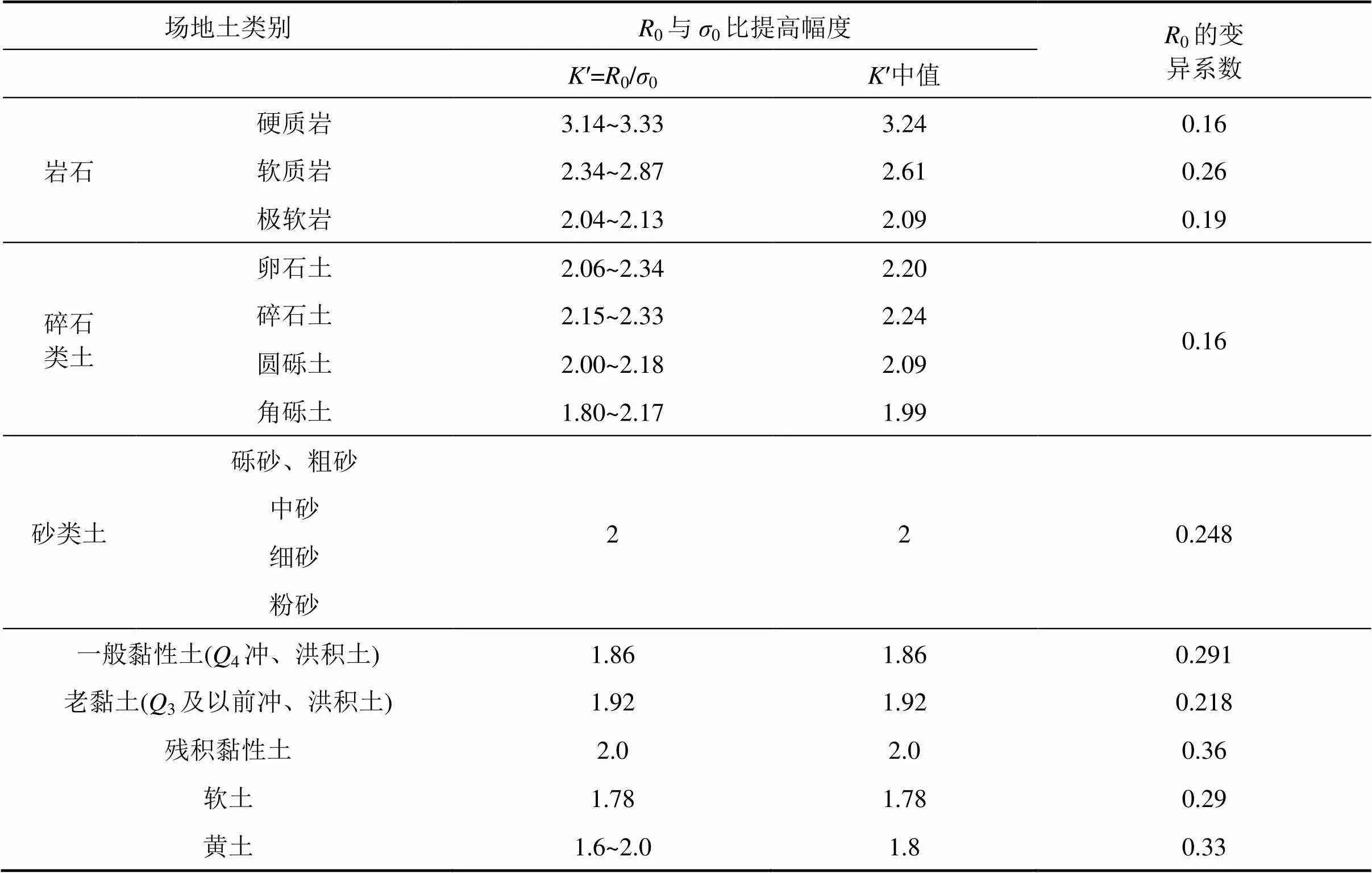
表2 地基土极限承载力基本值的特性

注：0为现行铁路桥涵设计规范中提供的承载力基本值

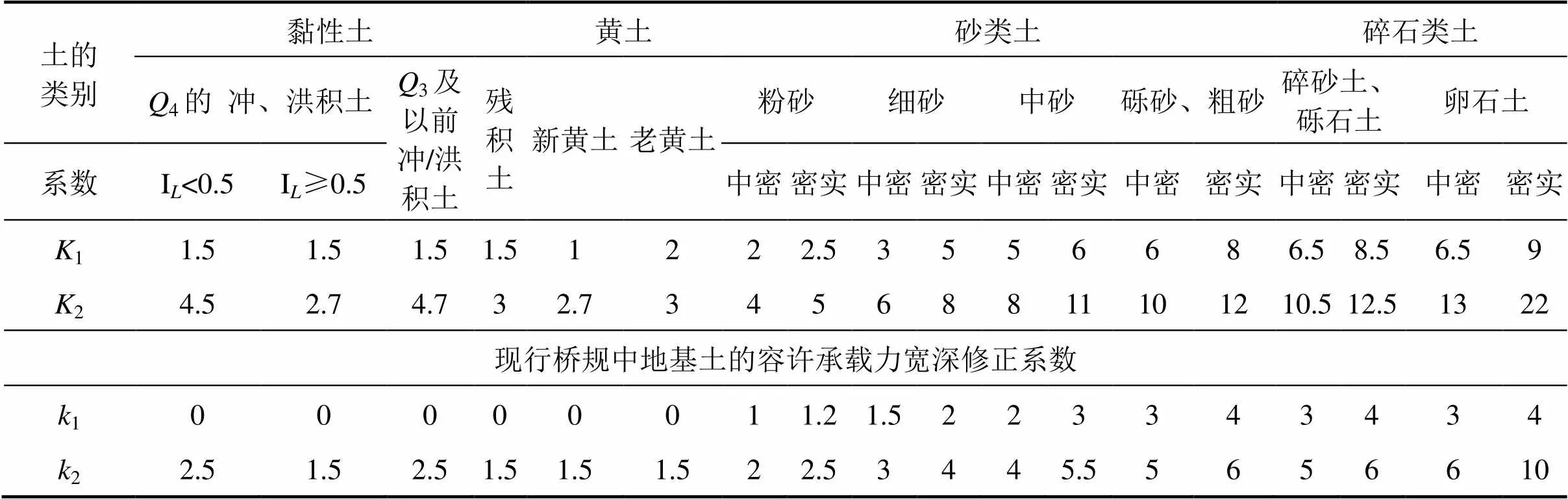
表3 地基极限承载力的宽深修正系数K1，K2

根据统计分析中的误差传递理论公式，可推导出式(8)中的变异系数，如式(9)所示。

式中：0的变异性已由“地基承载力标准值专题组”提出，如本文表2所示。

式(9)考虑了极限承载力的各因素的不确定性对极限承载力的变异系数的影响。由于1和2是根据与大量的试验和理论计算对比而得到的经验系数，可以不考虑其变异系数。一般地，0的变异系数比较大，为δ0=0.15~0.35，综合反映了地基土强度参数的不确定性；几何参数和的变异性较小，其范围为0.05~0.07；土容重的变异系数根据国内外的统计分析为δ=0.04~0.10。

取土容重的变异系数δ=0.07，几何参数变异系数约δ=δ=0.05，δ0=0.15~0.35，将以上数据代入式(9)得：δ=0.2~0.37，变异系数δ的中值约为0.3，这与国外绝大多数研究成果和国外可靠性理论规范校准时采用的数值是一致的[15]。

如果用集中力的方式对地基承载能力极限状态进行分析，这时除了考虑的各种变异系数以外，有时还应该考虑基础的尺寸变异性，即由于基础承载力极限值为×××。其中，和分别为基础的长度和宽度，得基础极限承载力P的变异系数为

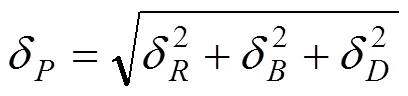
如果忽略基础尺寸的变异性，则的变异系数变为

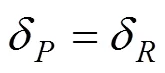
4 结论

1) 针对桥梁设计中的永久作用和可变作用的不确定性进行计算。除风力、列车活载产生的土压力、流水和冰压力外的其余荷载大小及其无量纲化系数均服从正态分布。风力服从极值I型分布，流水压力及冰压力目前缺乏统计资料，有待于进一步统计分析。

2) 地基土极限承载力的计算表达式采用“极限承载力基本值加宽深修正值”的模式。地基土极限承载力基本值0比0(规范中提供的承载力基本值)对于不同类别的土有不同的提高，提高幅度大致在2倍左右。

3) 根据统计分析中的误差传递理论公式，推导出地基极限承载力计算值的变异系数δ的中值约为0.3，这与国外绝大多数研究成果和国外可靠性理论规范校准时采用的数值是一致的。如果用集中力的方式对地基承载能力极限状态进行分析，还应该考虑基础的尺寸变异性。

4) 文中求得的作用荷载和地基土抗力的不确定性数值用于浅基础可靠度分析，其结果是合理的。在规范设计理念由容许应力法向极限状态法转变时，文中提供的地基极限承载力的宽深修正系数等内容可为可靠性理论规范的改进和修订提供基础数据。

[1] 纵雷. 岩土工程的可靠度研究浅述[J]. 中国新技术新产品, 2014, 10: 103. ZONG Lei. Discussion on reliability of geotechnical engineering[J]. China New Technologies and Products, 2014, 10: 103.

[2] 陈祖煜. 建立在相对安全率准则基础上的岩土工程可靠度分析与安全判据[J]. 岩石力学与工程学报, 2018, 37(3): 521−544. CHEN Zuyu. Reliability analysis and safety criterion in geotechnical engineering based on the index of safety margin[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3): 521−544.

[3] 李亚军, 刘斯宏, 傅中志, 等. 多层地基土坡的随机有限元模型不同参数比较分析[J]. 岩土工程学报, 2014, 36(1): 162−169. LI Yajun, LIU Sihong, FU Zhongzhi, et al. Comparative study on the effect of different parameters of random finite element models of an embankment supported by multilayered foundations[J]. Chinese Journal of Geotechnical engineering, 2014, 36(1): 162−169.

[4] WANG Y. Reliability-based design of spread foundations by Monte Calro simulations[J]. Geotechnique, 2011, 61(8): 677−685.

[5] LI S, ZHAO H B, RU Z. Slope reliability analysis by updated support vector machine and Monte Carlo simulation[J]. Natural Hazards, 2013, 65(1): 707−722.

[6] 张启兵. 岩土工程可靠性分析方法及应用发展现状[J] .安徽建筑, 2016: 154−156. ZHANG Qibing. Geotechnical engineering reliability analysis method and application development[J] . Anhui Architecture, 2016: 154−156.

[7] Reale C, Xue J, Gavin K. System reliability of slopes using multimodal optimization[J]. Geotechnique, 2016, 66(5): 1−11.

[8] 许红梅. 岩土参数的不确定性及取值分析[J] .中国水运, 2016, 16(1): 312−315. XU Hongmei. Uncertainty and value analysis of geotechnical parameters[J]. China Water Transport, 2016, 16(1): 312−315.

[9] 龚勋, 张冬梅. 二维空间随机场的浅基础极限承载力可靠度分析[J] . 地下空间与工程学报, 2012, 8: 1676− 1679. GONG Xun, ZHANG Dongmei. Reliability anlysis of allowable pressure on shallow foundation based on 2D random field[J]. China Journal of Underground Space and Engineering, 2012, 8: 1676−1679.

[10] 刘锡金. 对岩土工程进行系统的可靠度控制[J]. 山东工业技术, 2014, 21: 154−154. LIU Xijin. System reliability control for geotechnical engineering[J] .Shandong Industrial Technology, 2014, 21: 154−154.

[11] WANG Y, CAO Z. Expanded reliability-based design of piles in spatially variable soil using efficient Monte Carlo simulations[J]. Soils and Foundations, 2013, 53(6): 820−834.

[12] LI L, WANG Y, CAO Z J. Probabilistic slope stability analysis by risk aggregation[J]. Engineering Geology, 2014, 176: 57−65.

[13] 冷伍明. 基础工程可靠度分析与设计理论[M]. 长沙: 中南大学出版社, 2000: 61−91. LENG Wuming. Basic engineering reliability analysis and design theory[M]. Changsha: Central South University Press, 2000: 61−91.

[14] LI L, CHU X S. Multiple response surfaces for slope reliability analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(2): 175−192.

[15] 杨光华, 姜燕, 张玉成, 等. 确定地基承载力的新方法[J]. 岩土工程学报, 2014, 36(4): 597−603. YANG Guanghua, JIANG Yan, ZHANG Yucheng, et al. New method for determination of bearing capacity of soil foundation[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 597−603.

(编辑 涂鹏)

Analysis on the uncertainty of design variables of shallow foundation in railway bridge

ZHANG Weizhen

(Hunan Zhongda Design Institute Co., Ltd, Changsha 410075, China)

The calculation and analysis on the uncertainty of design variables is a basic work for revising some specifications in reliability-based codes. In this paper, a study on shallow foundation of railway bridge was carried out by using the probabilistic limit state design method based on the reliability theory, and the uncertainty for a series of design variables in engineering design was summarized and classified. On this basis, the uncertainty of the load effect and the ultimate bearing capacity of the foundation soil were mainly discussed. The mean value, the variance and the variation coefficient were determined for the dimensionless coefficients of the permanent and variable loads. The related data and the reliability principle were used to deduce the expressions for the correction coefficients of width and depth, and the variation coefficient of soil resistance under the limit state of the foundation soil. The results can be referenced and utilized for the revision of the reliability-based codes.

shallow foundation; design variables; uncertainty; reliability; coefficient of variation

10.19713/j.cnki.43−1423/u.2018.12.012

U24

A

1672 − 7029(2018)12 − 3106 − 07

2017−11−21

国家自然科学基金资助项目(51478478)

张威振(1979−)，男，山东安丘人，高级工程师，从事道路、桥梁、隧道设计与研究工作；E−mail：linquanzhang@yeah.net