大跨平坡屋盖风荷载折减的移动平均法
祝志文,程国用
大跨平坡屋盖风荷载折减的移动平均法
祝志文1, 2,程国用1
(1. 湖南大学 土木工程学院,湖南 长沙 410082;2. 汕头大学 土木与环境工程系,广东 汕头 515063)
根据大跨平坡屋盖脉动风压相干函数导出气动导纳函数,将气动导纳函数与滑动平均滤波器按照截止频率相等的原则进行等效匹配,推导出适用于大跨平坡屋盖风荷载折减的移动平均法。基于某博物馆大跨平坡屋盖风洞测压试验,对本文提出的风荷载折减方法合理性进行验证。研究结果表明:基于风洞试验的统计方法比规范方法在计算大跨平坡屋盖最不利设计风荷载方面更合理;而随着平坡屋盖结构尺寸的增大,最不利设计风荷载折减程度趋于稳定;本文提出的风荷载折减方法,能为大跨平坡屋盖结构最不利设计风荷载的合理确定提供参考。
大跨平坡屋盖;风荷载折减;气动导纳函数;移动平均法
脉动风压在建筑表面上的分布并不完全正相关,导致作用在结构不同部位处的脉动风压并不同时达到最大值。因此,随着围护结构尺度的增大,作用在围护结构上的总风荷载将会减小,这即是围护结构风荷载折减的尺寸效应[1]。对风荷载作用面积较大的大跨屋盖,其尺寸折减效应可能较显著。由于试验条件和费用的限制,在风洞试验中不太可能通过在建筑模型表面上布置十分密集的测压点进行空间积分以精确考虑围护结构风荷载折减的尺寸效应。目前,大跨屋盖一般通过风洞试验获得全部测点各自最不利风压进行屋盖的设计,并且各个测点最不利风压并非同一风向角下取值,由此确定的大跨屋盖风荷载可能明显偏大,因而结构设计可能是非常保守的。因此,需要考察脉动风压相关性随空间的变化,合理考虑大跨屋盖设计风荷载的折减,为大跨屋盖的设计提供合理的风荷载。移动平均法可折减作用在建筑上的风荷载[2]。该方法先对测点的风压时程进行滑动平均,再计算测点最不利风压并替代测点附属面积的风压极值,从而达到风荷载的折减。风洞试验基于此方法考虑风荷载折减时,无需在建筑模型表面上布置特别密集的测压点,这在大型结构风洞测压试验研究中,能合理减少测点数量并减少试验费用。移动平均法用于大跨屋盖风荷载折减的合理性与移动平均时间取值有关。Lawson[2]基于Royex House现场实测提出移动平均时间表达式,但Royex House属于低矮建筑物,其风压特性与大跨建筑物有较大差别。Holmes[3]基于Royex House现场实测得到的迎风墙上的脉动风压相干函数,给出移动平均时间表达式,但其在大跨屋盖上的适用性有待验证。大跨平坡屋盖结构是近年出现的大跨度结构形式,其平坡状上、下屋面坡度均很小,因而形成尖锐的气动外形,其风荷载特征尚无相关研究报道,因而,研究其风荷载折减特征对合理确定其最不利设计风荷载非常重要。本文基于某博物馆大跨平坡屋盖风洞测压试验数据,利用移动平均法,分析平坡屋盖风荷载折减变化规律,提出考虑折减效应后的大跨平坡屋盖最不利设计风荷载的计算方法,以期为大跨平坡屋盖最不利设计风荷载合理确定提供参考。
1 移动平均法
1.1 滑动平均滤波器
滑动平均滤波器可以对输入信号进行平滑,起到低通滤波的效果[4]。在输入信号为脉动风压信号时,输出信号(即滑动平均脉动风压信号)可表示为:
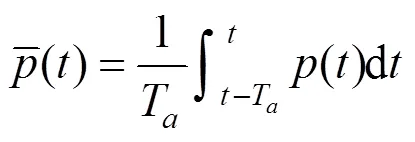
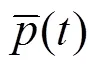
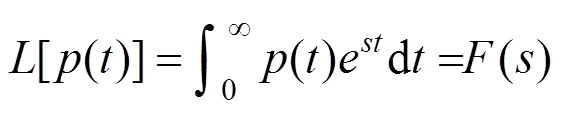
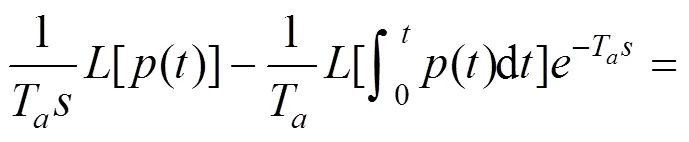
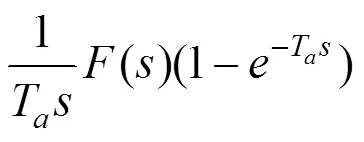
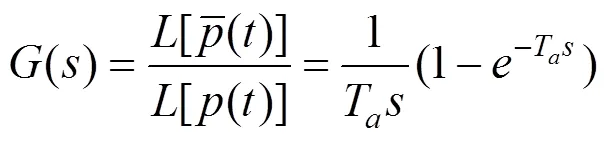
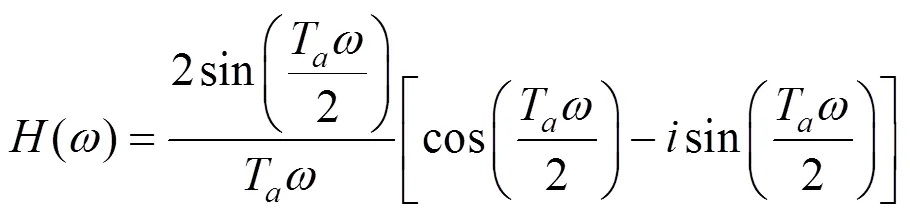
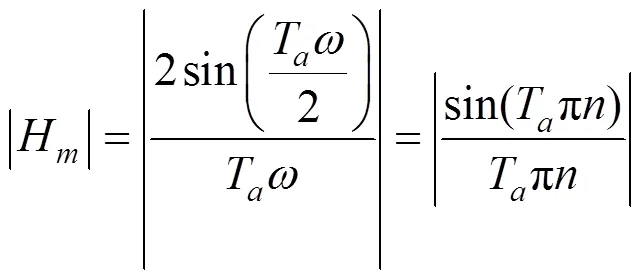
滑动平均滤波器幅值频率响应截止频率n(即−3 dB频率)的方程式如下[4]:
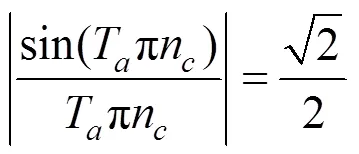
由式(7)可得到n为:
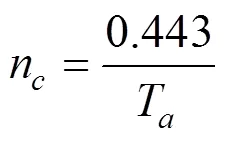
1.2 气动导纳函数
作用在大跨平屋盖上边长为×的矩形板单元上的脉动风荷载为:
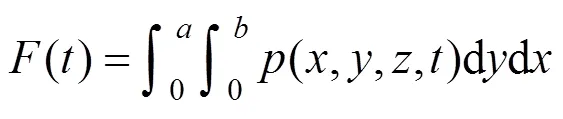
矩形板上的脉动风荷载互相关函数为:
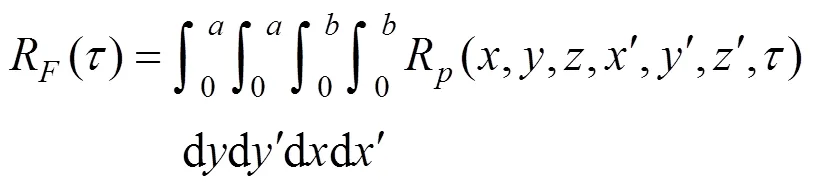
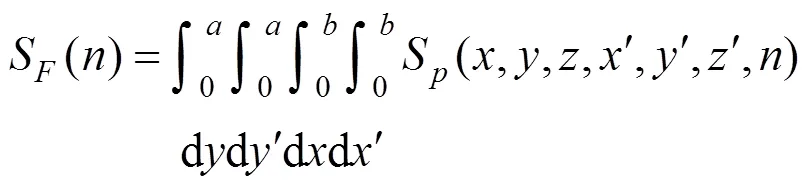
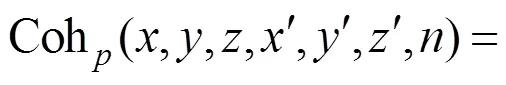
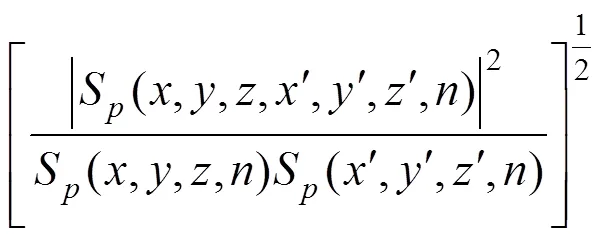
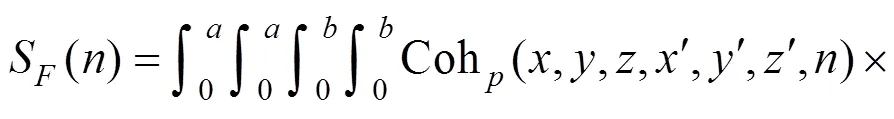
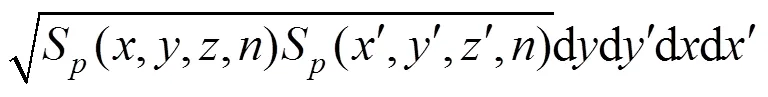
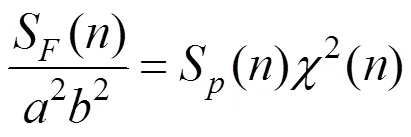
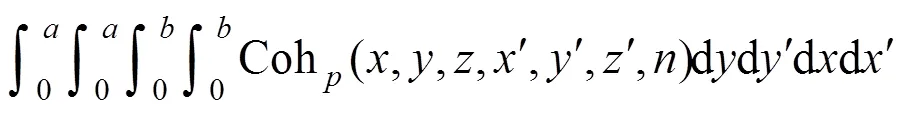
1.3 移动平均时间
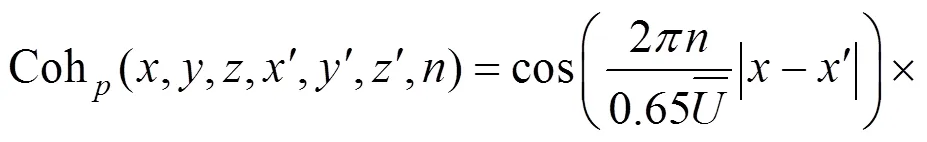
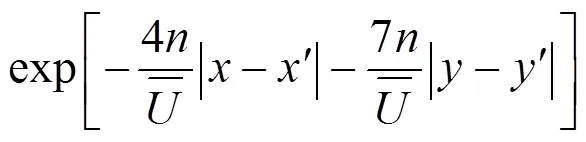
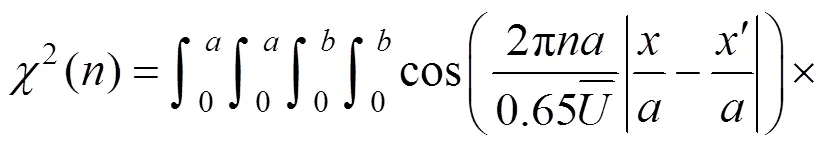
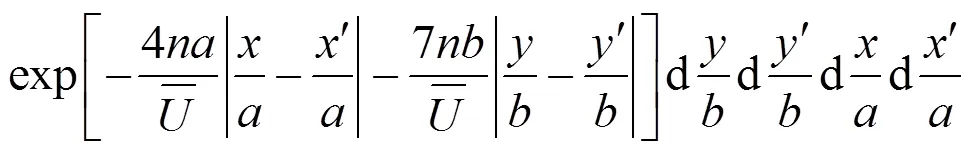
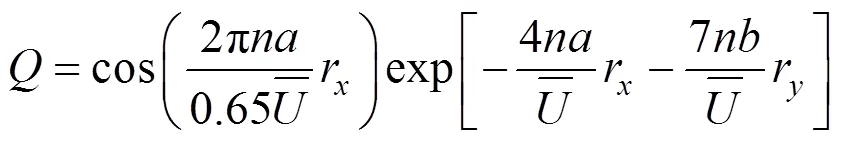
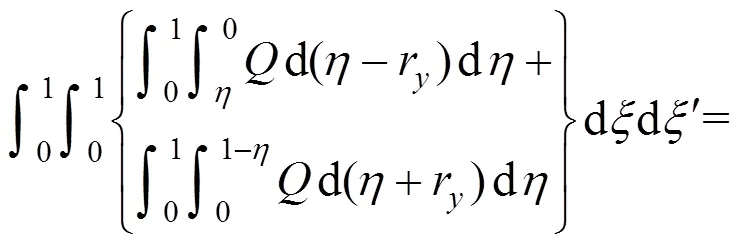
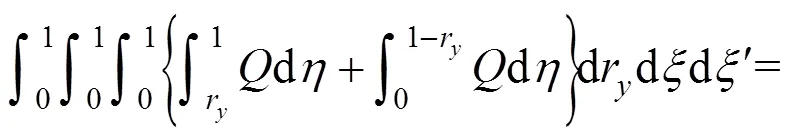
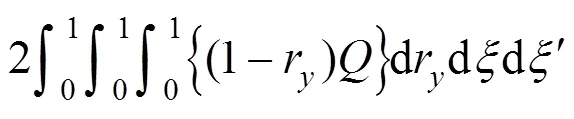
使用与式(18(b))相类似的处理过程,四重积分便可化为二重积分,即式(17)可以变为下列简化形式进行数值计算:
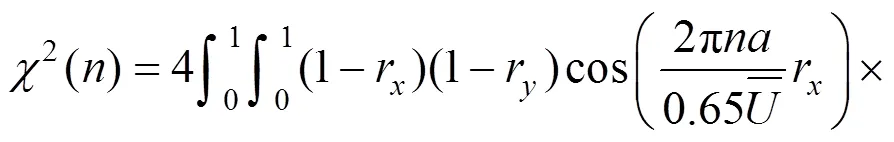

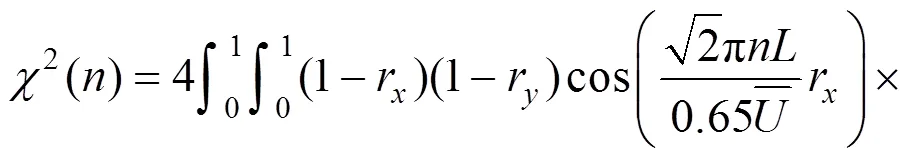
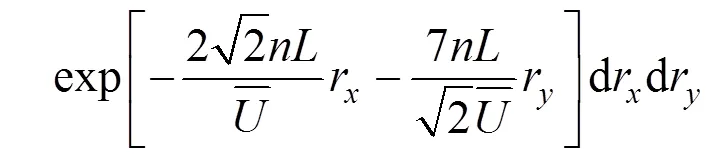
气动导纳截止频率n(即−3 dB频率)的方程式如下[4]:
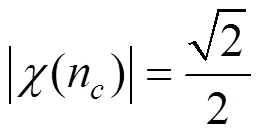
由式(20)和式(21)可得到n为:
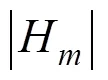
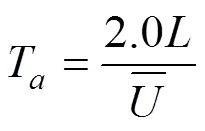
式(23)即为适用于大跨平屋盖风荷载折减的移动平均时间表达式。
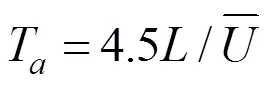
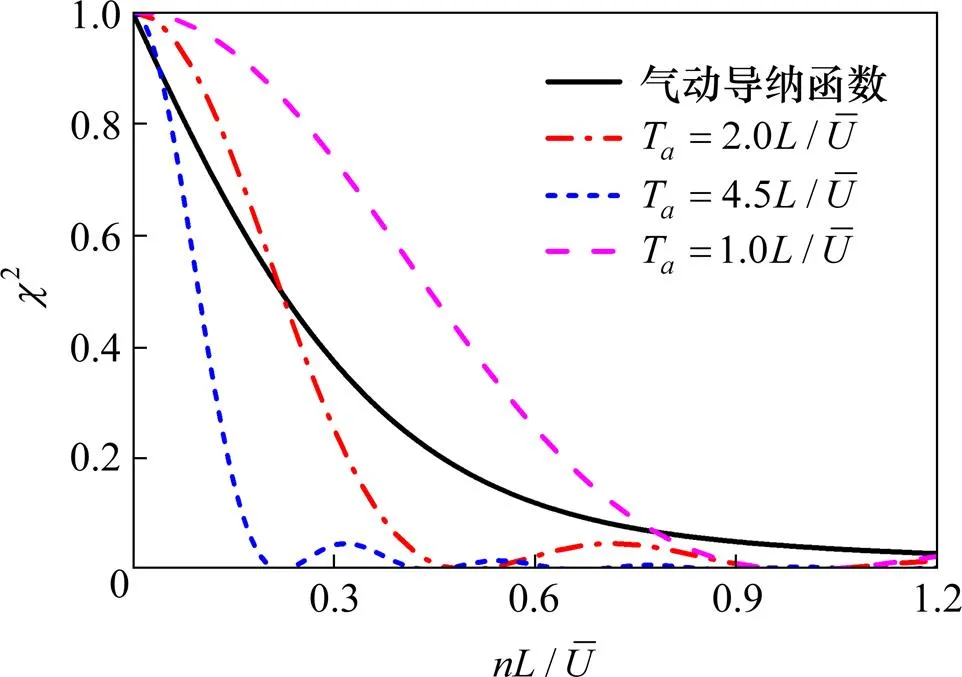
图1 气动导纳函数与等效滑动平均滤波器
2 风洞测压试验
2.1 试验概况
某博物馆改扩建工程项目(后称新博物馆)效果图如图2所示。新博物馆主体结构上的屋盖为大跨平坡屋盖,该屋盖东西向最大长度为144.4 m,南北向最大宽度84 m,屋盖顶部相对室外路面的高度为49.7 m,结构设计使用年限为100年。
新博物馆测压试验采用刚性模型,试验模型缩尺比为1:200,如图3所示。根据建筑外形和结构受力特征分别对模型平坡屋盖上下表面分块,屋盖分块如图4所示,部分测点布置如图5所示。

图2 新博物馆外景

图3 新博物馆风洞试验模型
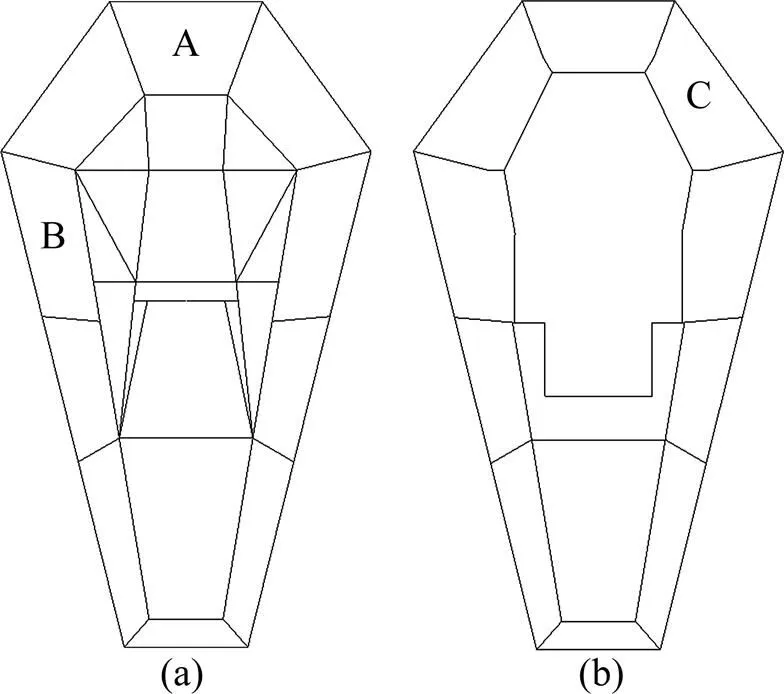
(a) 上表面;(b) 下表面
新博物馆试验风向角间隔为10°,共36个风向角,风向角定义见图6。采用二元尖劈和粗糙元来模拟B类地貌平均风速剖面和湍流度剖面,平均风速剖面和湍流度剖面如图7所示,图7中还显示了我国现行规范(GB50009—2012)[8]目标平均风剖面和湍流度剖面,在湍流度风剖面图中还绘制了日本规范(AIJ2004)[9]对湍流度剖面的要求。由图7可见,平均风剖面与规范目标风剖面吻合非常好,湍流度剖面与我国规范要求的剖面有一致的趋势性,在100 m高度以下湍流度值稍大于我国规范值(与日本规范相比,中国规范的湍流度值偏小),但基本满足规范对湍流度剖面的要求。动压和静压参考点设置在风洞转盘前方靠近风洞平面轴线位置,高度为0.3 m,通过眼镜蛇风速仪测定不同风向角下的风速和静压平均值。
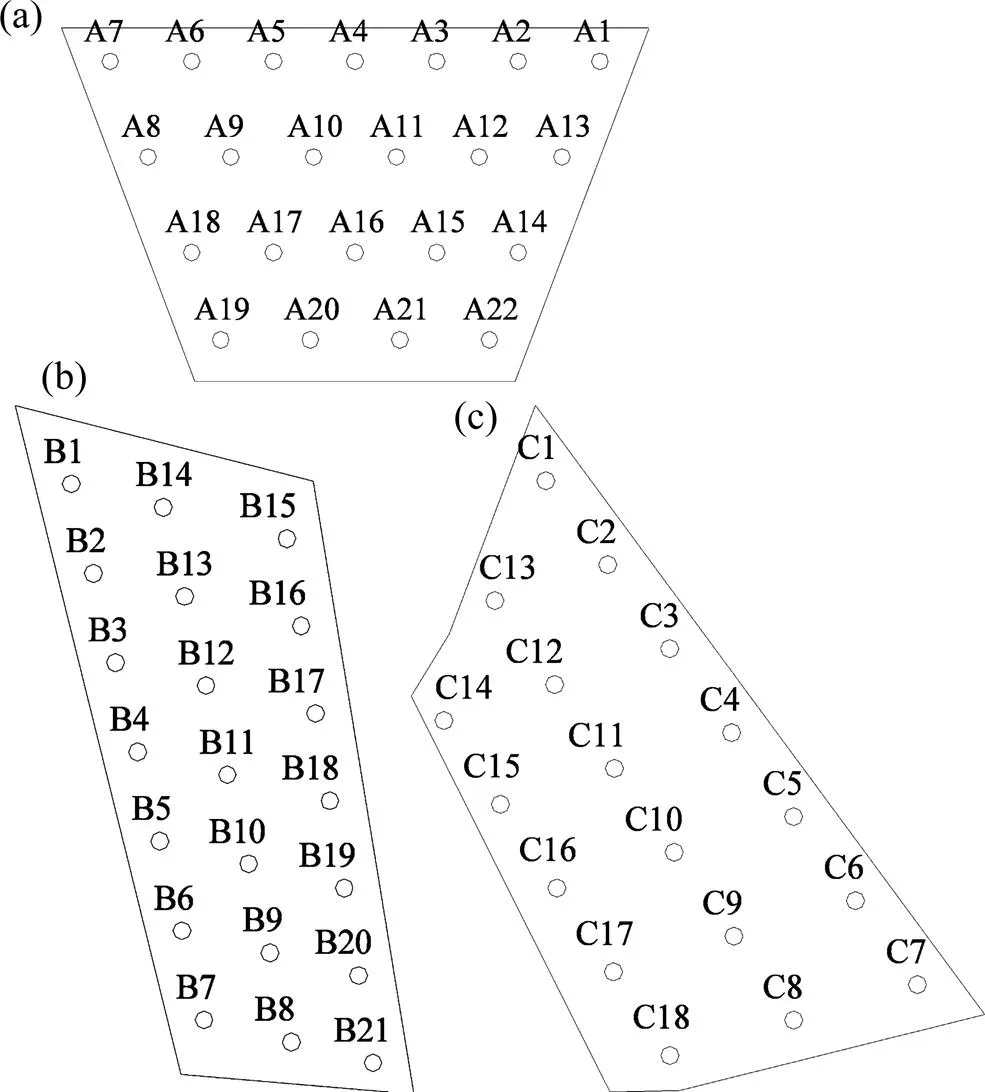
(a) A块测点布置;(b) B块测点布置;(c) C块测点布置
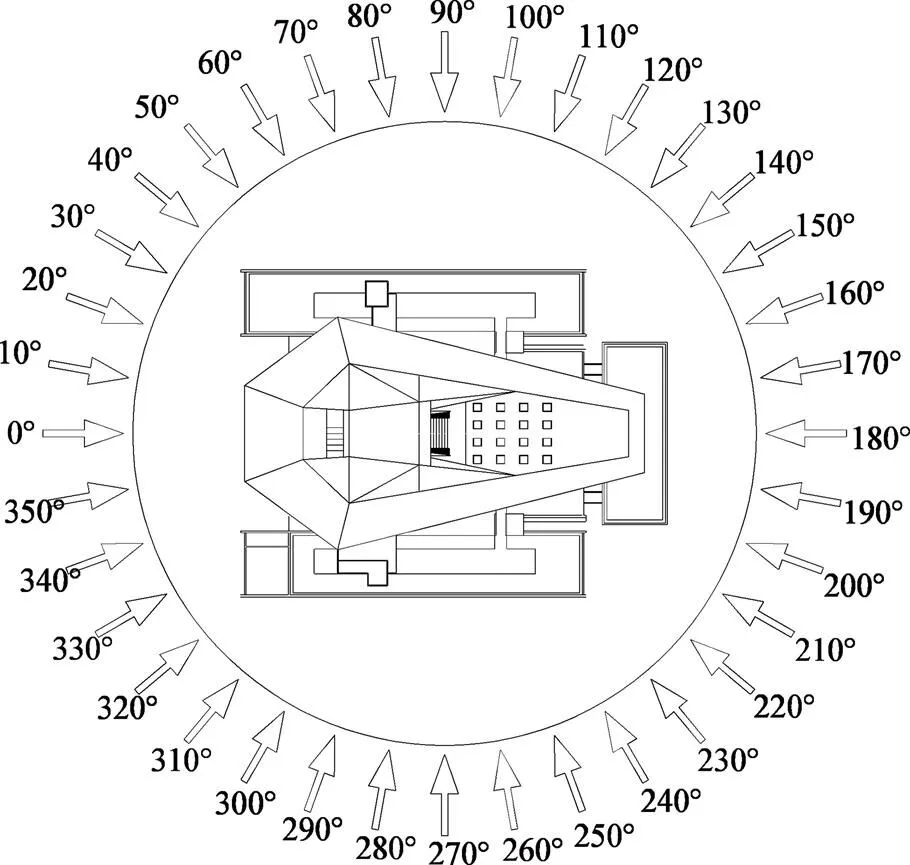
图6 试验风向角定义
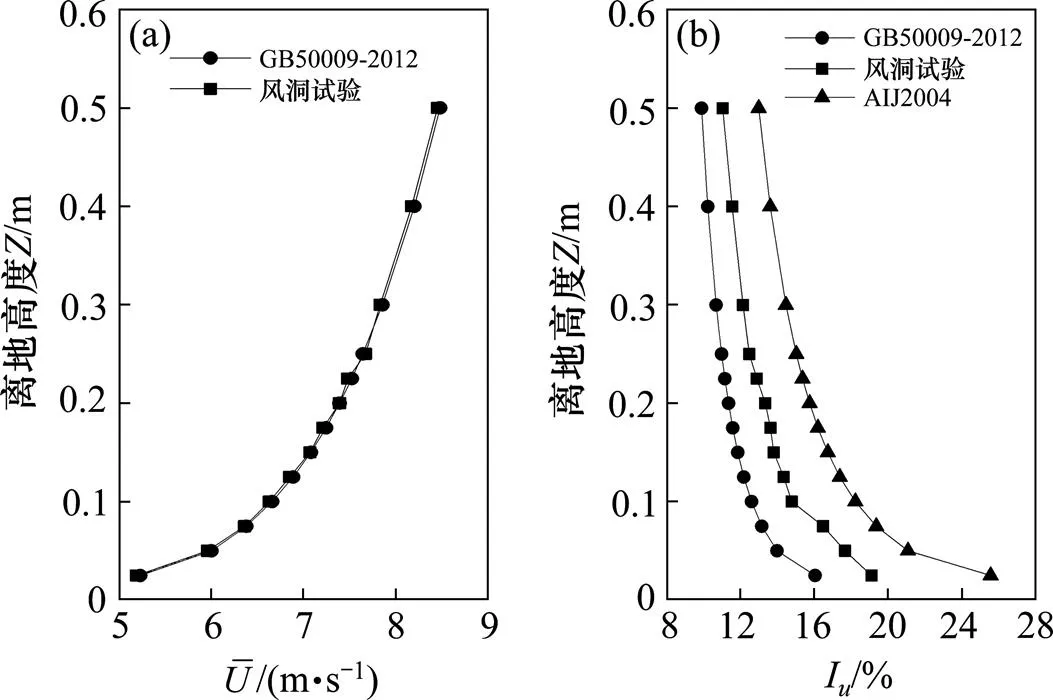
(a) 风剖面;(b) 湍流度剖面
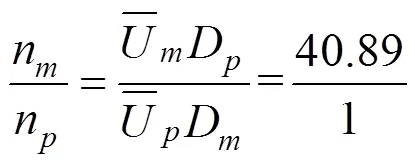
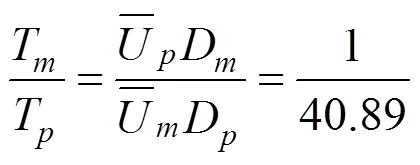
本试验测压信号采样频率312.5 Hz,采样时长32 s,则对应实际结构25.25 min采样时长。
2.2 数据处理
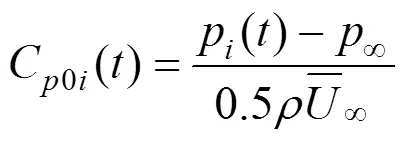
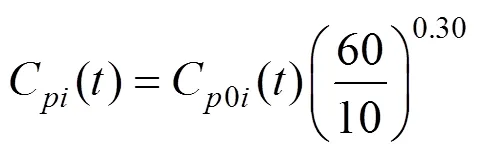
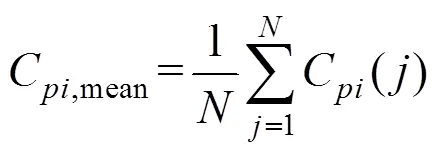
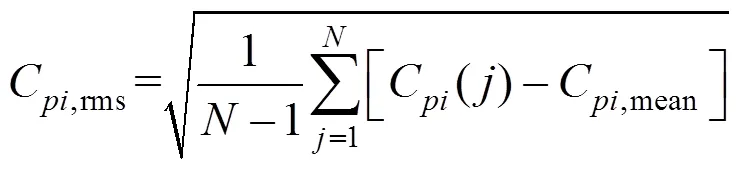
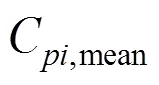
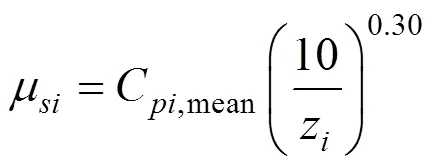
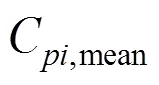
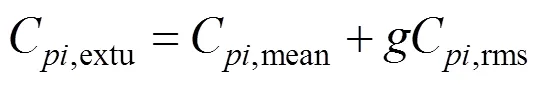
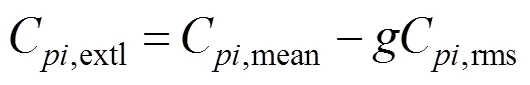
式(31)和式(32)中为峰值因子,在此取=3.5。对于每个测压点可以找到所有风向角下C,extu的最大值,称为该测点的最大极大值风压系数C,max,同理可以得到该测点的最小极小值风压系数C,min。
3 试验结果分析
3.1 统计方法和规范方法的对比
为比较统计方法和规范方法计算测点最不利风压值的大小,绘出2种方法计算A块各测点最不利负压值柱状图,如图8所示。由图8可见,大多数测点按照统计方法计算的最不利负压绝对值大于按照规范方法计算的最不利负压绝对值。同时,大跨屋盖表面的脉动压力受气流的分离、再附和漩涡脱落的影响较为严重。因此,在计算大跨平坡屋盖最不利设计风荷载时,只考虑来流的湍流特性和屋盖表面平均压力系数的规范方法可能并不可信,而基于屋盖表面风压统计特性的统计方法更合理。
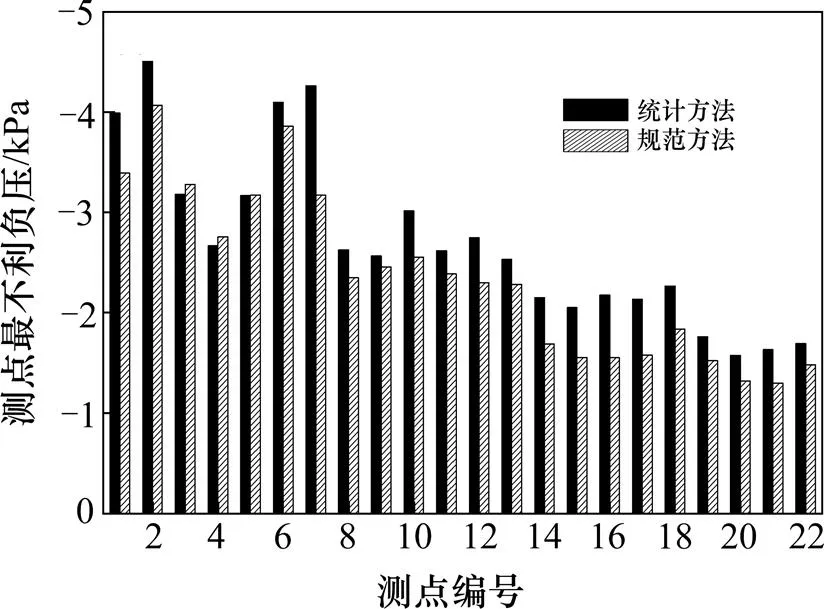
图8 在A块测点上统计方法和规范方法的对比
3.2 大跨平坡屋盖移动平均时间的选择
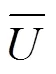

(a) ;(b) ;(c)
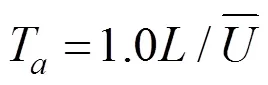
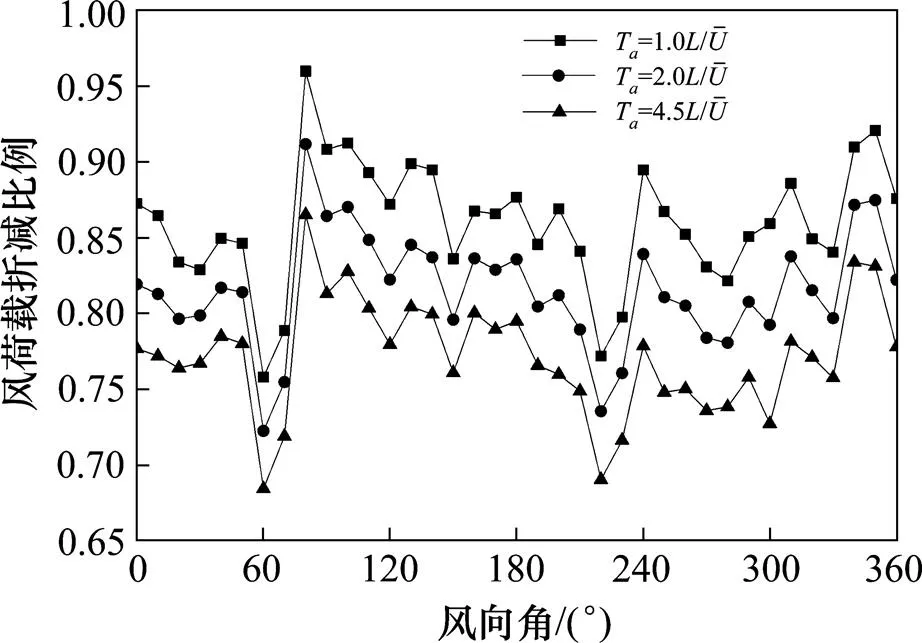
图10 在B块上风荷载折减比例随风向角变化曲线
3.3 大跨平坡屋盖风荷载尺寸折减因子
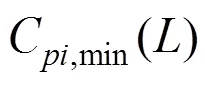
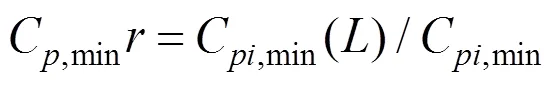
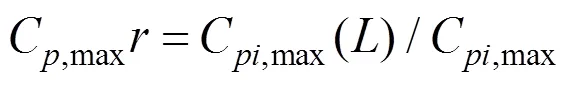
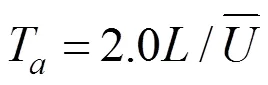
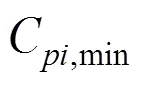
在实际应用中,可以先得到大跨平坡屋盖各测点的风荷载尺寸折减因子随特征尺寸的变化曲线,只要确定测点附属平坡屋盖的特征尺寸,便可以找到对应的风荷载尺寸折减因子,将得到的折减因子乘以最不利极值风压系数,按照统计方法计算便可得到考虑尺寸效应的大跨平坡屋盖结构最不利设计风荷载。上述基于移动平均的风荷载折减方法,可为大跨平坡屋盖结构最不利设计风荷载的合理确定提供有益的参考。
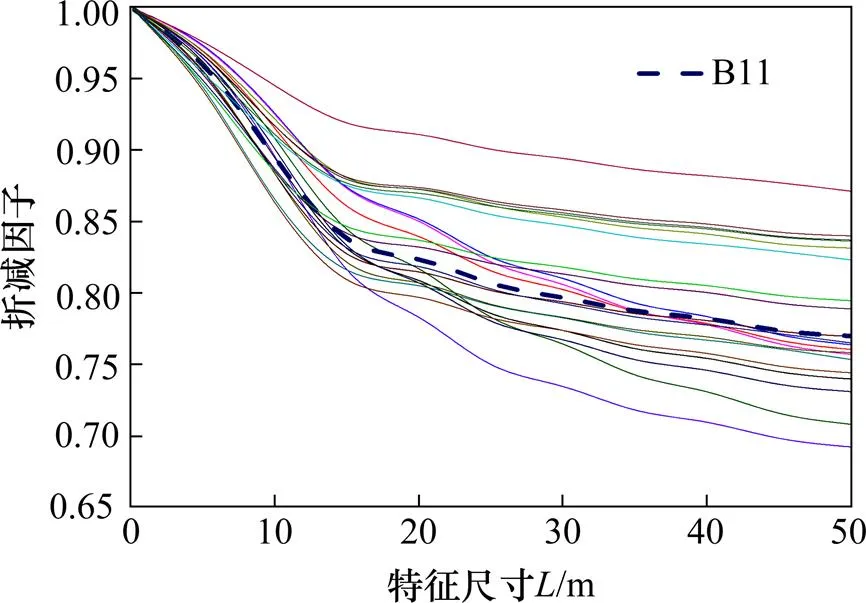
图11 B块各测点负压尺寸折减因子
4 结论
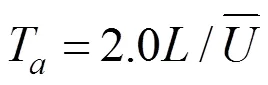
2) 统计方法考虑了脉动风压的统计特性,基于风洞试验的统计方法比规范方法在计算大跨平坡屋盖最不利设计风荷载方面更合理。
4) 随着平坡屋盖结构尺寸的增大,最不利设计风荷载的折减程度趋于稳定。
5) 基于大跨平坡屋盖风荷载尺寸折减因子曲线和最不利极值风压系数,并按照统计方法计算,可以方便得到考虑尺寸效应的大跨平坡屋盖结构最不利设计风荷载。
[1] Stathopoulos T, Surry D, Davenport A G. Effective wind loads on flat roofs[J]. Journal of the Structural Division, 1981, 108(2): 495−498.
[2] Lawson T V. The design of cladding[J]. Building & Environment, 1976, 11(1): 37−38.
[3] Holmes J D. Equivalent time averaging in wind engineering[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1997, 72(72): 411−419.
[4] Vegte J V D. 数字信号处理基础[M]. 侯正信, 王国安译. 北京: 电子工业出版社, 2003. Vegte J V D. Fundamentals of digital signal processing [M]. HOU Zhengxin, WANG Guoan, trans. Beijing: Publishing House of Electronics Industry, 2003.
[5] Dyrbye C, Hansen S O. Wind loads on structures[M]. New York: John Wiley & Sons, 1997.
[6] Uematsu Y, Moteki T, Hongo T. Model of wind pressure field on circular flat roofs and its application to load estimation[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2008, 96(6−7): 1003−1014.
[7] Greenway M E. An analytical approach to wind velocity gust factors[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1979, 5(1): 61−91.
[8] GB 50009—2012, 建筑结构荷载规范[S]. GB 50009—2012, Load code for the design of building structures[S].
[9] AIJ—2004. Recommendations for loads on buildings[S]. Tokyo: Architectural Institute of Japan, 2004.
[10] Holmes J D. Wind loading of structures[M]. 2nd ed. London: Taylor & Francis Group, 2007.
[11] 周晅毅, 顾明, 臧健, 等. 深圳机场T3航站楼风压特性研究[J]. 建筑结构, 2011, 41(1): 122−125. ZHOU Xuanyi, GU Ming, ZANG Jian, et al. Research on wind pressure of terminal 3 in shenzhen international airport[J]. Building Structure, 2011, 41(1): 122−125.
(编辑 阳丽霞)
Wind loading reduction on large-span flat roofs using moving average method
ZHU Zhiwen1, 2, CHENG Guoyong1
(1. College of Civil Engineering, Hunan University, Changsha 410082, China; 2. Department of Civil and Environmental Engineering, Shantou University, Shantou 515063, China)
Based on the expression of the coherence function of fluctuating wind pressure on the large-span flat roof, the aerodynamic admittance function was first presented. Then the moving average method for wind loading reduction on large-span flat roofs was provided after matching the cut-off frequency of the aerodynamic admittance to that of the moving average filter. Finally, the rationality of the present method was verified by using the pressure data on a flat-roof museum building from wind tunnel test. The research shows that, compared to the code method, the statistical method based on wind tunnel test data is more acceptable for calculating the most critical wind pressure on large-span flat roof; while with the increase on roof span, the wind loading reduction of a flat roof under the most critical scenario tends to be stable. The present method can provide a useful way to reasonably determine the most critical wind loading on large-span flat roof structures.
large-span flat roof; wind pressure reduction; aerodynamic admittance function; moving average method
10.19713/j.cnki.43−1423/u.2018.12.025
TU242.9
A
1672 − 7029(2018)12 − 3208 − 09
2017−09−28
国家重点基础研究发展计划(973计划)项目(2015CB057701);国家自然科学基金资助项目(51878269)
祝志文(1968−),男,湖南益阳人,教授,博士,从事工程结构抗风研究;E−mail:zhuzw@stu.edu.cn

