含能材料反应釜温度模型仿真辨识
陈冲,王冬磊,江沛,尹爱军,张智禹
(1.重庆大学 机械工程学院,重庆 400044;2.中国工程物理研究院 化工材料研究所,成都 621900)
反应釜广泛应用于石油、化工、医药、食品等行业,是用来完成硫化、硝化、聚合、缩合等工艺过程的压力容器。国内外对反应釜控制的自动化程度偏低,如何实现对反应釜温度的精确控制成为制造瓶颈,对反应釜在线控制技术的研究也越来越受到关注[1]。目前对于反应釜的在线控制技术如预测控制、优化控制等都是基于模型的控制策略,因此,实施在线控制的首要任务即建立准确的反应釜温度模型[2]。受投料数量和种类的影响,反应釜中存在一系列复杂的反应,如成球工艺蒸溶阶段乙酸乙酯溶液蒸发的吸热效应[3],使得反应釜的温度动态特性具有时变性、非线性、大时滞的特点[4],很难根据反应的动态特性和平衡方程进行机理建模。文献[5]采用机理建模的方法通过分析夹套式反应釜的结构对蒸汽加热过程中的热传递方式建立了发射药反应釜传温模型,建模过程繁琐,模型适应性差。
近年来,基于系统正常运行过程中输入和输出数据的实验建模方法广泛应用于工业控制领域[6],而最小二乘法(RLS)通过最小化误差的平方和来寻找数据的最佳函数匹配,加入遗忘因子后能克服“数据饱和”现象,实现时变过程的参数辨识[7]。文献[8]根据系统开环实验获得的数据,利用最小二乘方法对模型进行辨识,并在 SIMULINK中进行了仿真实验。文献[9]采用自整定遗忘因子对含有有色噪声的时变系统进行了系统辨识,有较强的实时跟踪能力和较高的估计精度。
文中以含能材料成球工艺反应釜为研究对象,对收集到的历史数据进行预处理,基于机理建模的原理得到系统模型结构。利用遗忘因子最小二乘法(FFRLS)对系统模型参数进行辨识,得到含能材料反应釜温度模型,为实现反应釜温度在线控制提供预测模型。
1 反应釜结构特点
成球工艺是含能材料生产线上最重要的一道工艺,将直接决定成球尺寸,影响产品质量。目前采用如图1所示的夹套式反应釜完成含能材料的成球,通过设定电机转速,调节蒸汽阀门开度来控制反应釜的温度,进而间接控制产品成球的尺寸。电机转速在成球过程中基本处于恒定状态,因此反应釜温度控制系统可以简化为单输入单输出(SISO)系统。其中控制量为阀门开度,输出量为反应釜内温。

图1 反应釜结构
2 系统辨识方法
2.1 递推最小二乘法
递推最小二乘法的基本思想就是在前次估计的基础上,利用被控对象不断提供的新的输入输出数据来修正模型参数,提高辨识精度,递推算法可概括为:
被控对象的模型采用 ARX(Autoregressive Exogenous)模型为:

式中:y(k)和 u(k)为系统的输入输出量;d为时滞系数;w(k)为白噪声。
系统离散传递函数为:
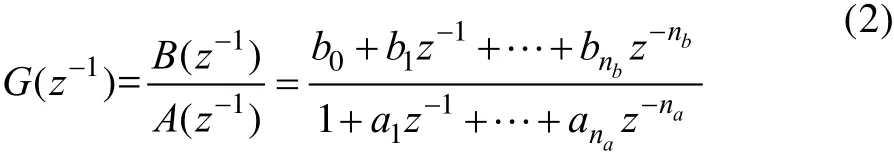
参数估计即用系统输入/输出数据来确定 A(z-1)与B(z-1) 的系数。
将式(1)改为最小二乘形式:

取性能指标:


令:

代入式(5),则k时刻的最小二乘估计可表示为:
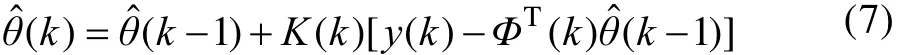
式中: K( k )=P( k) Φ ( k) 。

2.2 遗忘因子递推最小二乘法
递推最小二乘法适用于定常未知参数系统[10-11],其在参数时变系统中有其局限性。随着数据的增长,将出现“数据饱和”现象。即随着时间的推移,新数据所提供的信息被淹没在长期积累的旧数据中,修正作用变得越来越弱。故为提高新数据的计算权重,利用带遗忘因子对数据施加时变加权系数,最新的数据以1加权,前n个采样数据以λn加权,降低旧数据的信息量,保证新数据的有效性,由式(4),其性能指标变为:

同理,其递推公式如下:

3 仿真验证
3.1 模型分段
以差分方程为数学模型来描述和分析反应釜温度特性,在各种扰动因素下反应釜温度控制系统具有非线性、时变性等特性,控制难度大。同时该系统还具有大时滞、大惯性的特点。随着含能材料生产中不断投料和发生各种物理反应,系统的时滞和惯性不断变化,系统辨识的难度加大。在含能材料反应釜温度模型辨识中,采用浙大中控DCS系统对反应釜温度、阀门开度等数据进行采集,采样具有时间间隔,为离散模型,辨识模型取如式(1)所示的ARX模型。
含能材料成球工艺分为混棉、升温、溶解、成球、预蒸、脱水、蒸溶和冷却出料八个工序,如图2所示,其中t1至t2为升温工序,t3至t4处于成球工序,t5至t6处于蒸溶工序,t1、t3、t5前一段时间内,阀门开度为0,反应釜内温基本处于平衡状态,t1、t3、t5时,阀门开度发生阶跃变化,反应釜内温变化曲线可看作阶跃响应曲线。
升温工序前,混棉工序内反应釜需要加入水、硝化棉及溶剂等原材料,混棉完成后反应釜内温降为θ1作为温度模型的第一段初始点。溶解工序需要加入室温存放的明胶试剂,导致反应釜内原材料成分、含量及温度发生改变,反应釜内温降为θ3,作为温度模型第二段初始点。脱水工序需要加入室温存放的盐水试剂,反应釜内温降为θ5,作为温度模型的第三段初始点。除去添加原料带来的模型时滞系数突变,在成球工艺过程中,由于溶剂蒸发,将会造成模型参数随时间缓慢变化。

图2 成球工艺反应釜内温及阀门开度变化趋势
3.2 时滞系数
图 2 中,t1、t2、t3、t4、t5、t6为温度发生变化时的时间节点,阀门开度变化时间皆在上述节点,这与反应釜温度模型具有大时滞的特点相符。取不同日期的成球工序生产历史数据,并加以分析计算,去除扰动带来的偶然性误差,对阀门开度变化时刻与温度变化时刻时间间隔取均值,得到温度变化对阀门开度变化的滞后时间,见表1。由于其他时刻无法保证阀门开度变化前反应釜内温处于平衡状态,无法观测到反应釜内温的大时滞特性,为方便计算,取 θ1~θ3内温度模型滞后时间τ1=240 s,θ3~θ4内温度模型滞后时间τ2=210 s,θ5~θmax内温度模型滞后时间 τ3=150 s。时滞系数d=τi/h,其中h为仿真步长。
3.3 仿真研究
成球工艺中,反应釜为一个参数时变系统,由于物理反应,系统模型参数随时间不断缓慢变化。同时由于投料混棉、溶解、脱水工序前的投料,模型时滞系数发生突变。由式(10)可知,模型时滞系数对模型参数的辨识无影响,由不同时滞系数将反应釜温度系统分成三段后,对每段模型皆可以 FFRLS进行仿真辨识。
以FFRLS对参数突变与参数时变问题进行辨识,借用Maltab进行仿真计算[12]。具体仿真步骤如下:
1)已知 d、na、nb,确定参数、P(0)与遗忘因子λ,并输入初始数据;
2)采样当前输入u(k)与输出y(k);
4)k=k+1,返回2),循环。
考虑如下仿真系统: y( k ) + a1y( k - 1) + a2y( k - 2)=b0u( k -τ ) + b1u( k -τ- 1) + w( k )。式中,w(k)为方差为0.1的白噪声。系统模型参数突变时,取对象参数θ( k )= [a1, a2, b0, b1]T为:


表1 温度滞后时间(节选)
其中L为仿真步数,由历史数据得三个工序分别间隔3 h,取仿真步长为h=10 s,则L=1080。遗忘因子0.9<λ<1,λ越小,跟踪能力越强,λ越大,收敛精度越高。文中取遗忘因子 λ=0.975,θˆ(0)=0,P (0)=106I。辨识输入信号采用M序列,其性质近似于白噪声,可保证良好的辨识精度,工程上也易于实现。采用 FFRLS算法进行参数估计,参数突变与参数时变系统仿真结果如图3、图4所示。
利用FFRLS,在系统参数突变和时变情况下,对系统进行参数辨识。因为输入信号 M序列为随机信号,为消除随机误差,进行10次仿真。由图1可知,仿真开始后1 min内辨识参数波动较大,即取仿真开始6步后的数据,分别计算各参数均方根误差,并对其取平均值,结果见表2。可以看出,除去参数突变时b1均方根误差为18.69%,其他皆小于10%。模型参数中a2辨识效果最好,b1辨识效果最差。
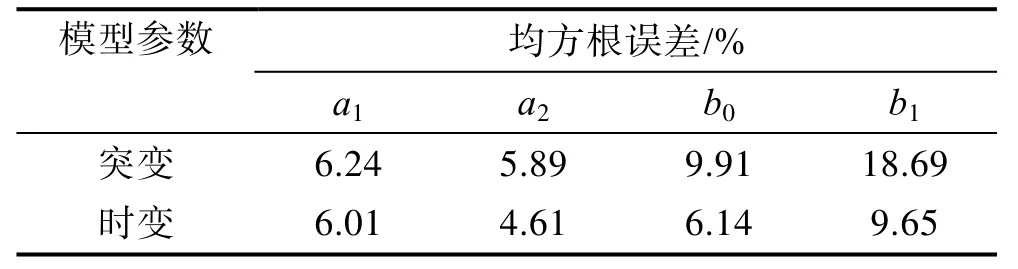
表2 模型参数均方根误差

图3 突变系统参数辨识

图4 时变系统参数辨识
4 结论
1)由于成球工艺生产过程中分阶段的投料和不断进行的物理反应,系统模型具有突变和时变特性。对于模型时滞系数的突变,可采用分段模型进行辨识;对于模型参数的时变,可采用 FFRLS进行实时修正。
2)FFRLS能克服“数据饱和”现象,实时地跟踪参数的变化,且相较于参数突变系统,该算法更适合对参数慢时变系统进行参数辨识。
3)通过加入合适的自适应算法,在系统模型参数突变情况下,遗忘因子先减小以提高追踪能力,靠近真实值时,遗忘因子增大,提高算法收敛精度,可提升对模型参数突变系统的辨识效果。

