基于二级近似的航天器结构的模型修正方法

李建宏宇，庞贺伟

（1. 北京卫星环境工程研究所 可靠性与环境工程技术重点实验室，北京 100094；2. 中国空间技术研究院，北京 100094）

航天技术的进步和任务需求的扩展，特别是遥感卫星分辨率性能指标的不断提高，对航天器结构的动力学模型的准确性要求越来越高[1]。在轨微振动环境影响遥感卫星的分辨率，因此对于微振动分析，不仅要求航天器结构的动力学模型的模态频率准确，还需要提高频率响应计算的准确性。

根据动力学实验产生的频率响应对结构的动力学模型进行修正是提高模型精度的重要方法[2-3]。模型修正问题实际是一个结构优化问题[4]，目标是最小化实验实测数据和分析结果数据之间的误差。模型修正理论应用到航天器结构中，将面临严重的效率问题。对于航天器结构，其有限元模型的自由度数达到十万[5-6]，甚至更高，对其进行频率响应分析需要耗费大量的计算成本和存储成本。因此直接对航天器有限元模型进行修正，需要的时间成本是不可接受的。

模型缩聚[7]最早提出是用于提高大规模有限元模型的结构动力学分析的计算效率和减少计算机存储空间的使用，是一种近似模型。近些年，模型缩聚主要用于基于试验测量的模型修正，将模型缩聚到实验测量的自由度上，缩聚后动力学模型自由度的个数等于实验测量自由度的个数。动力学实验中传感器的数量和位置受实验条件的限制，影响缩聚后模型的精度。缩聚后的模型往往只能近似表达低频段的动力学特征，无法正确反映中高频段的动力学特征。

文中首次利用二级近似算法，在模型修正过程中高效率地计算结构参数修改后结构的频率响应，并建立多重优化流程消除近似计算引入的误差。

1 频率响应及其敏度的近似计算

1.1 一级近似计算

Ritz法的基本假设是用r个n维形状向量{Ψi}和幅值αi线性表示位移向量，写成矩阵形式为：

在模型修正过程中，以初始结构的前r阶特征向量为形状向量来表示结构的位移响应。设初始结构的刚度矩阵为[K0]，初始结构的质量矩阵为[M0]。则形状向量满足条件：

动刚度矩阵为：

在载荷{F(ω)}的作用下，结构的位移向量频率响应为：

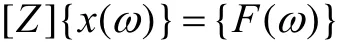
将Ritz法带入动力学方程并左乘[Ψ]T：

可以得到位移的频率响应：

其中：

设：

得到位移的频率响应的一级近似计算公式：

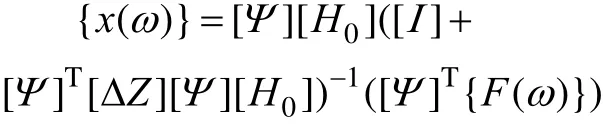
对于结构参数p的敏度公式为：

一级近似计算公式中，矩阵运算为 r阶矩阵运算，而 r远小于结构的自由度数，所以具有较高的计算效率。

第一级近似引入的误差分为两部分：

1）由于仅考虑前 r阶模态的叠加，产生的截断误差。可以通过增加r值的大小，减少误差，同时r值增大将降低计算效率。一般经验，r可以根据动力学实验的频段进行选择。动力学试验测量的最高频率点为m Hz，则计算频率小于3m Hz的所有模态。

2）模型修正过程中对结构参数进行调整后，结构的特征向量也发生变化并导致前r阶特征向量组成的Ritz空间也发生相应变化。考虑到航天器有限元模型建模技术比较成熟，模型修正过程中仅对模型的结构参数进行微小调整。结构参数修改前后的Ritz空间是相近的，同时，可以引入多重优化流程来消除近似计算的误差。

1.2 频率响应函数及其敏度的二级近似计算

文中采用一种改进的Hermit插值方法[8]。其形式与 Hermit差值类似，通过增加非线性参数 r来提高插值的准确性。设 F（ x）为原函数，（ x）为近似函数；x的维数为n；h个已知原函数函值和敏度值的点xj。构造如下的近似函数）：

[Ψ]T[Δ Z ][Ψ]和[Δ Z]与结构参数的非线性关系是相同的，同时[Δ Z ]与结构参数的非线性关系是可以预测的，且大部分是代数式关系。典型的结构参数如材料的弹性模量、密度、板厚、杆的截面积等，与[Δ Z]均为线性关系。可以根据结构参数的属性确定 r值。通过二级近似后，频率响应的计算效率得到了提高。

2 优化模型与多重优化流程

模型修正问题为无约束的优化问题。目标函数是描述理论模型特性和实验模型特性相关程度的一个表达式。文中采用Zang[9]引入的频率响应相关性指标准则作为目标函数：

拟牛顿法是无约束最优化方法中最有效的一类算法。其优点为：迭代中仅需要一阶导数，具有二次终止性，对于一般情况，具有超线性收敛速率。文中将采用拟牛顿法作为优化算法。

图1为多重优化流程。该流程的优点是通过两次引入近似计算，提高目标函数的计算效率，同时通过多重优化保证优化结果的准确性。

图1 多重优化流程

3 数值算例

3.1 GARTEUR梁的模型修正

以 GARTEUR梁结构为算例进行模型修正。GARTEUR梁结构如图2所示，为平面钢架结构。有限元模型由74个节点、78个梁单元构成。每个节点的自由度为 3，为 x，y两个方向的平动自由度和 xy面的转动自由度。其材料参数为：E=7.5×1010N/m2，ρ=2.8×103kg/m3，μ=0.3。梁截面面积为：水平梁Sx=0.004 m2，竖直梁 Sy=0.006 m2，对角梁 Sd=0.003 m2。各梁的截面惯性距均为I=0.0756 m4。

图2 GARTEUR梁结构

选取结构中的21个自由度测量频率响应。在1,2节点的y方向施加振幅为1×106N的正弦载荷，对结构在频段5~505 Hz进行频率响应分析。为了构造动力学实验产生的频率响应数据作为参考值，采用更加密集的网格划分并使用直接法分析频率响应。通过模态分析可知，结构小于1515 Hz的频率共有41阶。

以梁的截面积作为模型修正需要修正的结构参数。初始结构的梁截面面积为：水平梁Sx=0.005 m2，竖直梁Sy=0.005 m2，对角梁Sd=0.005 m2。目标函数的迭代曲线如图3所示，经过18次迭代，模型修正结束。在整个模型修正过程中，进行了2次模态分析和4次结构动刚度矩阵的组装，其他迭代计算都是近似计算。为模型修正前后结构参数的误差。

3.2 CMG平台的模型修正

某卫星CMG平台由超过380 000个有限单元和110 000个节点组成。有限元模型的自由度数超过370 000，CMG平台有通过5组共15个隔振器与底座连接，隔振器有限单元属性为 PBUSH，局部模型如图4所示。以PBUSH的刚度为模型修正的结构参数，对结构在频段1~300 Hz进行频率响应分析，近似计算中取结构前200阶模态。

图3 目标函数迭代曲线

表1 模型修正结果

图4 隔振器与底座的局部模型

经过360次迭代，模型修正结束。在整个过程中，进行了3次模态分析，17次动刚度矩阵组装，360次近似计算。整个模型修正过程中计算时间成本分布见表2。模型修正前后典型测量点的位移频率响应如图5所示。模型修正后，频率响应曲线的误差得到了明显改善。

表2 计算时间成本分布

图5 模型修正前后典型测量点的位移频率响应

4 结语

航天器结构自由度数高且结构复杂，在模型修正过程中不易对有限元模型直接进行修正。文中基于特征向量构建Ritz空间，并推导出结构频率响应的近似计算公式。之后根据动力学实验的频段选择相应的模态阶数来减小截断误差，通过多重优化算法消除近似误差。引入近似函数计算动刚度矩阵，减小迭代过程中的计算成本和存储成本。两个数值算例证明了该方法的准确性和高效性，因此该方法适用于实际航天器结构模型修正的工程应用。