全桥型DC/DC变换器的DMC-PID串级控制策略研究
王利波,余明扬,王一军
(中南大学信息科学与工程学院,长沙 410075)
DC/DC变换器,如Buck变换器、单端反激变换器和多级开关组合变换器等的拓扑结构众多,它们均属于典型的开关非线性系统[1-4],显然选用经典控制理论的线性控制策略不是最优的控制方案。然而长期以来,DC/DC变换器所采用最多的控制方法就是线性PID控制,尽管该控制系统结构设计简单,通用性较好,但将其应用于非线性的DC/DC变换器会使得系统的动态响应慢,控制特性差,无法实现优化控制和高精度控制。
为解决上述问题,文献[5]提出采用基于状态反馈线性化的最优控制,该控制方法的静态误差小,对负载扰动具有较强鲁棒性,但该控制方案对所建模型的准确性要求较高,模型失配会降低控制效果;文献[6]运用自适应PID串级控制,通过仿真表明该方案对系统的寄生参数要求不高且能获得较好的控制性能,但需要对参数进行在线估计,一些实时扰动会影响估计的精度;文献[7]采用模糊PID控制以克服环路时延对系统瞬态响应的影响,但对控制量因子和PID控制参数的选取较为复杂。
针对上述问题,本文以全桥型DC/DC变换器为研究对象,提出了基于输入输出状态反馈线性化的DMC-PID串级控制策略。运用状态空间平均法,推导出变换器的非线性模型,根据微分几何方法得到其单输入单输出的仿射非线性控制系统,由状态反馈线性化将非线性系统线性化。从而将复杂的非线性控制问题转化为线性系统的控制问题,这样就可以设计线性控制器来镇定系统。本文基于预测控制方法,提出了DMC-PID串级控制,该控制策略只需得到线性系统的阶跃响应,实现简单,相较于常用的PID-PID串级控制策略,具有较为优秀的控制性能。
1 全桥型DC/DC变换器状态空间平均模型
图1为全桥型DC/DC变换器的拓扑结构,其电源的输入电压为Uin,输出电压为Uo;IGBT开关管Q1~Q4组成全桥逆变电路;肖特基二极管D1、D2组成半波不控整流电路,电感L和电容C组成LC滤波电路。
为了获得良好的滤波性能,滤波电路中的电感L和电容C的取值尤为关键。C越大,其吸收的基波电流越大,电阻负载时会加重开关器件和整流器件承受的电流负担,同时电容的体积也会增大;C越小,动态性能优秀,但滤波性能较差[8]。同理,电感参数的选取也会受上述因素的影响,故需综合考虑,选取合适的滤波电容和滤波电感。主电路的参数如表1所示。
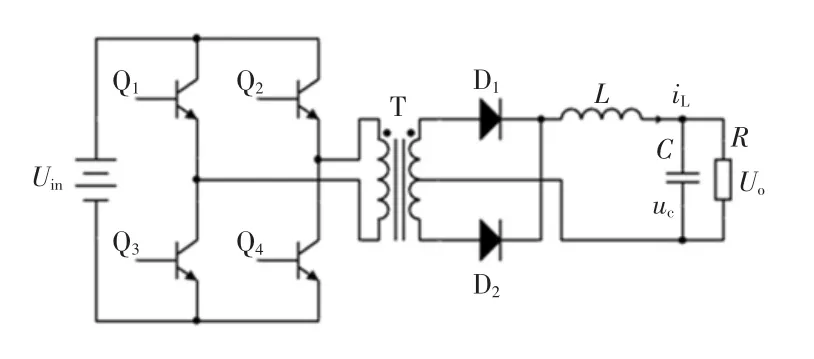
图1 全桥DC/DC变换器拓扑Fig.1 Topology of full-bridge DC/DC converter

表1 主电路参数Tab.1 Parameters of main circuit
上述等效电路如图2所示[9-11],为了综合考虑滤波电容的等效串联电阻、开关管开通与关断的死区效应以及直流母线电源的等效串联电阻等因素的影响,引入等效电阻Rd,Upwm为半桥整流输出电压。

图2 等效电路Fig.2 Equivalent circuit
选取电感电流iL和电容电压uC为状态变量,则选择开关函数 K(s)为:K(s)=1-s,其中:s取 0 或1。s=0表示全桥桥臂中点输出正电压或负电压,s=1表示桥臂中点输出零电压。
依据图2,可得该系统双输入单输出的状态空间方程[12-13]为

式中:Ui为直流母线电压;n为变压器一次侧、二次侧和三次侧的变比;io为负载电流。
应用状态空间平均法构成数学模型为
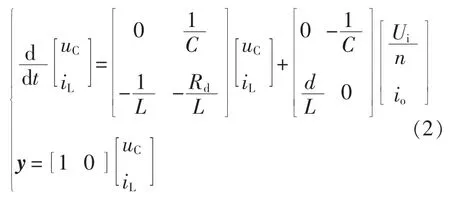
式中,d为开关管驱动脉冲占空比。
2 变换器的状态反馈精确线性化
由式(2)可知,系统的输出电压即电容电压uC是受输入电压Ui控制的,但在实际系统中,输入电压是不具可控性的,系统输出电压uC的稳定是通过调节脉冲占空比d实现的,因此d才是系统实际的控制输入。
通过分析系统的状态空间平均模型可知,该系统呈典型的仿射非线性,为了避免使用复杂的非线性控制策略和获得实际的控制输入,需要通过坐标变换将其线性化。
选取状态变量x=[x1x2]=[uCiL],输入变量u=d,输出变量 y=h(x)=x1,则可得变换器 SISO 仿射非线性状态空间方程为

根据微分几何理论,求解上述系统的导数和系统的关系度,即
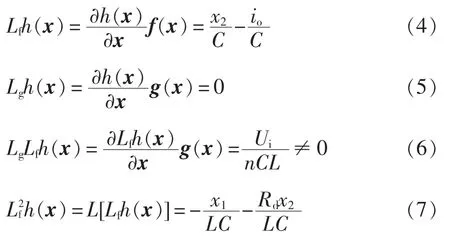
由式(6)可知,系统的关系度r=2是等于系统的阶数的,满足文献[14-15]中精确线性化的条件。因此可以通过如下的非线性坐标变换将系统线性化,即

则得到新的线性系统为

式中,v为线性系统新输入。在此坐标系下的状态控制率为
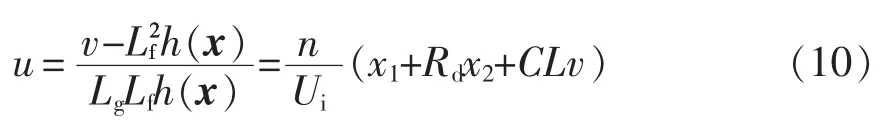
3 DMC-PID控制器的实现
DMC-PID串级控制的结构如图3所示,其副回路的控制对象为G2(s),采用频率较高的数字PID控制,主要是为了克服进入对象的二次干扰,减小干扰引起的偏差幅值,同时有利于主回路DMC的设计;主回路的控制对象为G1(s)和副回路组成的广义对象(图3中虚框所示),采用DMC算法,主要目的是获得良好的跟踪性能和较强的鲁棒性。

图3 DMC-PID控制结构框图Fig.3 Control block diagram of DMC-PID
依据式(9)的线性化模型,可得系统的传递函数为

则令:G1(s)=G2(s)=1/s。
在常规PID控制中,微分环节具有的预测功能和积分环节的消除静差功能都可以由DMC算法更好地替代,因此,在副回路的PID控制中通常只需要加入比例环节。又由于副回路采用的是数字PID控制,故可以采用工程整定方法,如响应曲线法、扩充临界比例法等来确定PID控制参数。
在确定了PID控制器的参数后,可得DMC算法的控制对象为

其中,KP为PID比例参数。
对式(12)的单位阶跃响应进行采样,令采样周期为T0,得DMC算法的预测模型向量a=[a1,a2,…,aN],N为建模时域。在M个连续控制增量Δw(k),…,Δw(k+M-1)的作用下,未来时刻的输出值为
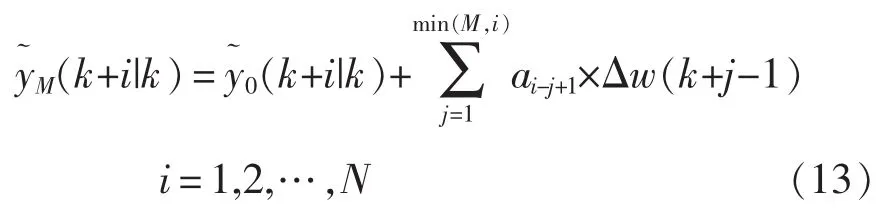
在控制过程中,为了能够平滑地调节脉冲占空比和获得稳定的输出电压,取优化性能指标为
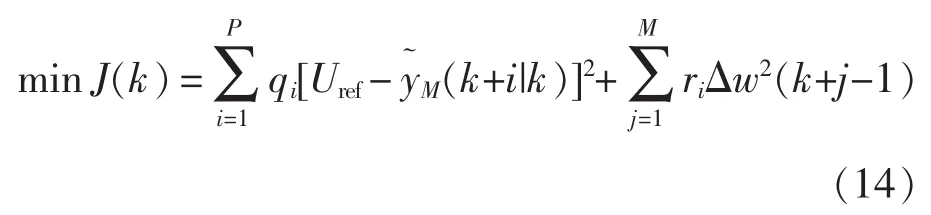
式中,qi和ri为权系数。求解无约束条件下的一系列最优解为
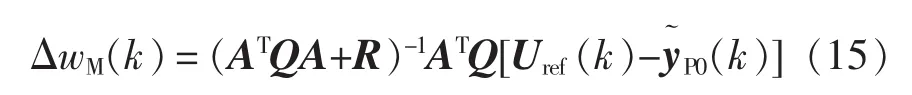
由于脉冲占空比有一定的调节范围,一般设为0.1≤u≤0.45,T为采样周期,Ui(k)为输入电压采样值,uC(k)为电容电压的采样值,iL(k)为电感电流采样值,则得
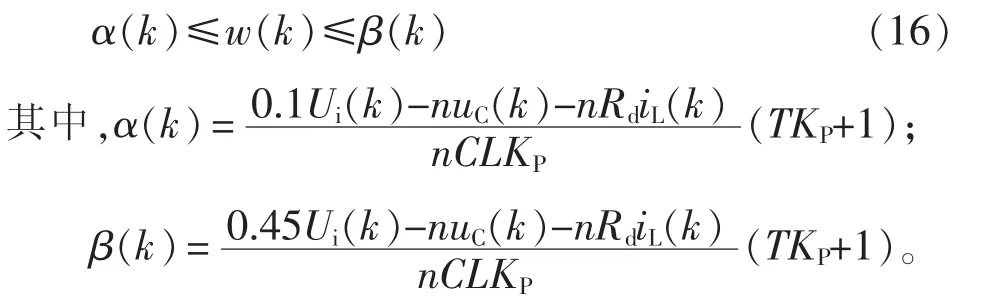
依据上述约束条件筛选出符合条件的最优解,将破坏约束条件的最优解修正上一采样时刻的最优解,得到局部最优。
得到在约束条件内的最优解w(k)后,采样同一时刻的输入电压 Ui(k)、电容电压 uC(k)和电感电流iL(k),通过坐标变换得到实际最优控制量——脉冲占空比u(k),并作用于全桥DC/DC直流电源以取得最优的控制效果。占空比的计算公式为

4 仿真与实验结果
为验证上述控制策略的有效性和优越性,对图1所示的全桥DC/DC直流电源系统同时进行DMC-PID和PID-PID串级控制算法的仿真和实验验证。主电路的参数如下:Ui=500 V,L=180 μH,C=20 μF,Rd=0.01 Ω,开关管开关频率为 20 kHz,输出电压期望值为27 V,负载电阻R=0.5 Ω。电压电流的采样频率为200 kHz。经过多次仿真实验,得到如下PID参数能使两种控制算法的控制性能达到最优。DMC-PID串级控制的内环参数为:KP=80,KI=KD=0;PID-PID 串级控制的内环参数为:KP1=1,KI1=KD1=0,外环参数为:KP2=8,KI2=0.7,KD2=0.4。对于输出端负载突变和输入电压突变,分别对全桥DC/DC直流电源的DMC-PID控制算法和PID-PID控制算法的控制特性进行仿真分析和实验验证。
4.1 仿真分析
图4和图5为2种控制算法的仿真结果,在仿真过程中将负载突变和输入电压突变当作外界干扰来处理。图4(a)为输入电压突变的调节过程,依次为:①2 ms时,Ui从 500 V跳变到 550 V;②3.5 ms时,Ui从 550 V 跳变到 500 V,图4(b)为 DMCPID控制量w的变化曲线。图5(a)为负载突变的调节过程,依次为:①2 ms时,R从0.5 Ω跳变到2 Ω;②3.5 ms 时,R 从 2 Ω 跳变到 1 Ω,图5(b)为DMC-PID控制量w的变化曲线。
在图4(a)中,当输入电压从500 V突变到550 V和从550 V突变到500 V时,DMC-PID控制算法输出电压的超调量分别为7.4%和2.4%,达到稳定的时间分别为0.5 ms和0.3 ms;PID-PID控制算法输出电压的超调量分别为5.1%和1.6%,达到稳定的时间分别为0.9 ms和0.9 ms。在图5(a)中,当负载电阻从0.5 Ω突变到2 Ω和从2 Ω突变到 1 Ω时,DMC-PID控制算法输出电压的超调量分别为3.6%和1.7%,达到稳定的时间分别为0.4 ms和0.2 ms;PID-PID控制算法输出电压的超调量分别为2.5%和1.1%,达到稳定的时间分别为0.9 ms和0.8 ms。
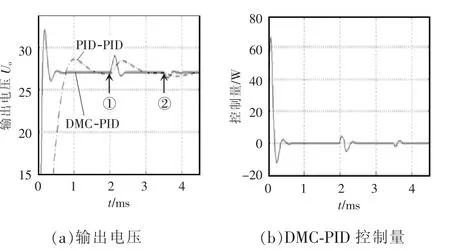
图4 输入电压突变仿真结果Fig.4 Simulation results of input voltage mutation

图5 负载突变仿真结果Fig.5 Simulation results of load mutation
由以上仿真结果可知,DMC-PID串级控制算法的超调量稍大于PID-PID串级控制算法,但其达到稳定的时间远远少于PID-PID串级控制算法。由此可知,DMC-PID串级控制具有更快速的响应速度和更优秀的快速性和稳定性。
4.2 实验结果
为了验证DMC-PID串级控制策略的实际控制效果,对其进行实验验证,并与PID-PID串级控制算法进行比较。实验的参数设置与仿真参数保持一致,控制算法由DSP实现,DSP的输出脉冲经驱动电路加载到开关管的C级和E级,霍尔传感器完成输出电压、输入电压和电感电流的采集,并将采集到的输出电压数据送至示波器显示。图6(a)为输入电压从500 V跳变到550 V时,运用DMC-PID串级控制算法的输出电压波形;图6(b)为相同条件下运用PID-PID串级控制算法的输出电压波形。图7(a)为负载电阻从 2 Ω 跳变到 1 Ω,运用 DMC-PID串级控制算法的输出电压的波形;图7(b)为相同条件下运用PID-PID串级控制算法的输出电压波形。
由图6可知,DMC-PID串级控制和PID-PID串级控制的输出电压达到稳定的时间分别为1.5 ms和3.2 ms,超调量分别为9.4%和8.9%。由图7可知,DMC-PID串级控制和PID-PID串级控制的输出电压达到稳定的时间分别为0.8 ms和1.8 ms,超调量分别为11.1%和9.3%。实验结果和仿真结果基本一致,对比两种控制策略的仿真和实验结果,验证了DMC-PID串级控制算法运用到全桥DC/DC直流电源系统能够更为快速地实现对输出电压的精确控制,具有更为优良的控制特性。

图6 输入电压突变输出电压波形Fig.6 Waveforms of output voltage when input voltage is mutated

图7 负载电压突变输出电压波形Fig.7 Waveforms of output voltage when load voltage is mutated
5 结语
本文将非线性系统转换为线性系统,从根本上解决了线性控制技术应用于开关电源上的不足。通过坐标变换将非线性转换为线性模型,选择DMCPID串级控制策略,计算出最优的控制量,最终将其转化为系统的实际控制量——开关管驱动脉冲的脉宽,使得系统获得了良好的鲁棒性和较强的抗干扰能力。通过对DMC-PID和PID-PID这两种控制方法的仿真分析和实验对比,验证了所提控制策略的可行性和优越性。
对比仿真和实验的结果可知,实际实验电压稳定的时间和超调量均差于仿真结果,这是因为数字控制的响应时间和电流电压的采集时间造成的。
本文所提出的基于状态反馈精确线性化的DMC-PID控制策略应用于其他拓扑结构的DC/DC变换器时,要根据情况加入微分环节和积分环节,只加入比例环节可能达不到理想的控制效果。

