基于PID控制的磨粒流机床液压缸压力变化的研究

盛亮，李俊烨，张红伟，孟文卿，何洋，李丹妮

（1.长春理工大学 机电工程学院，长春 130022；2.长春设备工艺研究所，长春 130012）

随着科技的快速进步，工业领域的发展逐渐倾向于精密和超精密加工方向，磨粒流加工（简称AFM）技术是一种非常具有代表性的精密加工方法，广泛应用于具有微小孔及复杂内曲面工件的精密加工[1]。通过磨粒与工件接触进行微摩擦到微切削的过程来达到工件内表面光整加工的目的，从而提高工件的加工精度[2]。磨粒流加工效果在很大程度上取决于磨粒流机床的整体性能和加工精度，而磨粒流机床控制系统是磨粒流加工机床的控制核心[3-5]。因此，控制系统的稳定性是保证被加工工件精度与质量的重要因素[6，7]。PID控制凭借其参数便于整定、结构改变灵活等特点，在众多工业控制中得到了广泛的应用[8-10]。

目前，磨粒流机床控制系统大多采用普通PID控制，然而，普通PID控制并不能保证机床整体性能和加工精度，因此，本文采用基于遗传算法优化下的积分分离式PID控制，通过分析机床液压缸压力的变化，对比普通PID控制和基于遗传算法优化下的积分分离式PID控制的模拟效果，探讨遗传算法优化后的积分分离式PID算法对机床控制系统的影响，为磨粒流机床控制系统的稳定性提供一定的理论基础和技术支持[11，12]。

1 磨粒流机床液压系统的基本组成及原理

磨粒流机床液压系统主要是由油泵、液压缸、液压阀、液压油和滤油器等辅助元件组成，其中液压缸是由液压缸筒、液压缸盖、液压缸活塞杆、缓冲和排气装置等组成，加工时，液压泵的转动带动活塞杆运动，磨料受到活塞杆的挤压对工件进行加工。其主要的工作流程为：当液压泵正转时，活塞杆上移，停止加工；当液压泵反转时，活塞杆下移，开始对工件进行加工。如图1所示。

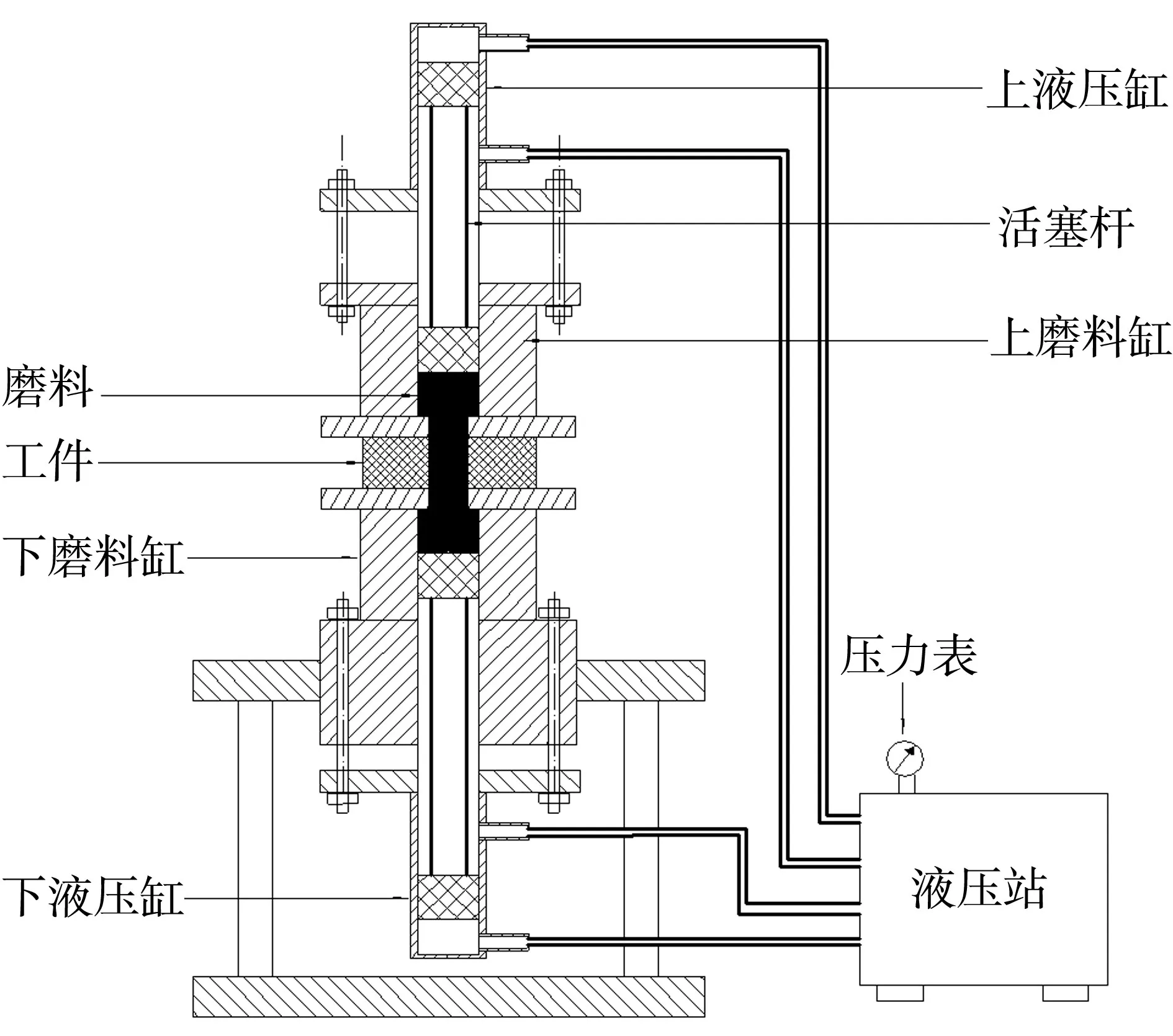
图1 磨粒流机床示意图

由于液压缸属于非线性单元，在运动过程中非常容易受到外界因素的干扰，随着液压泵的工作环境和负载的实时变化，其控制系统的参数也会发生持续波动，控制性能会受到较大影响，因此，液压缸控制系统模型如图2所示。

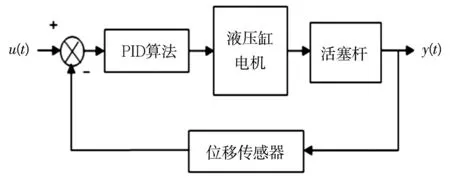
图2 液压缸控制系统模型

当给定系统输入信号u(t）时，此时输出量为y(t），当液压缸位置传感器测量出y(t）后，将输出量y(t）和输入量u(t）进行比较，然后将偏差量进行相应的算法处理，驱动液压泵正、反转促使活塞杆做往、返运动。在闭环控制下如此反复调整相应的误偏差，直到最终误偏差值为零。

1.1 液压缸活塞杆模型

液压缸活塞杆的移动是通过双向泵将液压油推向单向阀，从而使液压缸活塞杆做上下往复运动。活塞杆上、下运动的模型分别为：

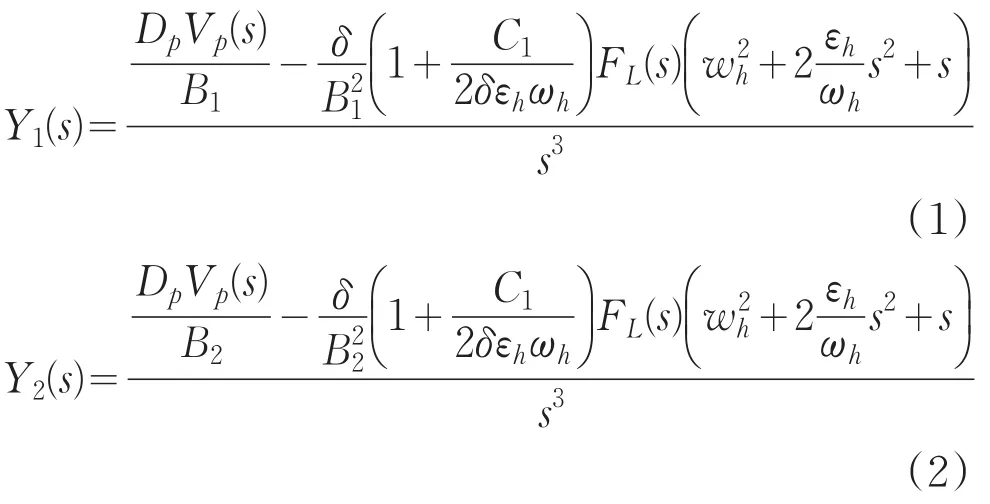
其中，Dp为双向泵液压油排量；B1、B2为液压缸活塞杆上、下表面横截面面积；δ为密封系数；C1为液压缸体积；FL(s)为负载；εh为阻尼系数；ωh为固有频率；Vp为运动速度。

2 磨粒流机床液压缸PID控制系统

2.1 普通PID控制器设计及原理

普通PID控制器以其控制方法简单、可靠性强，且参数设置简单方便等优点，大量应用于自动化控制系统中，其控制流程如图3所示。

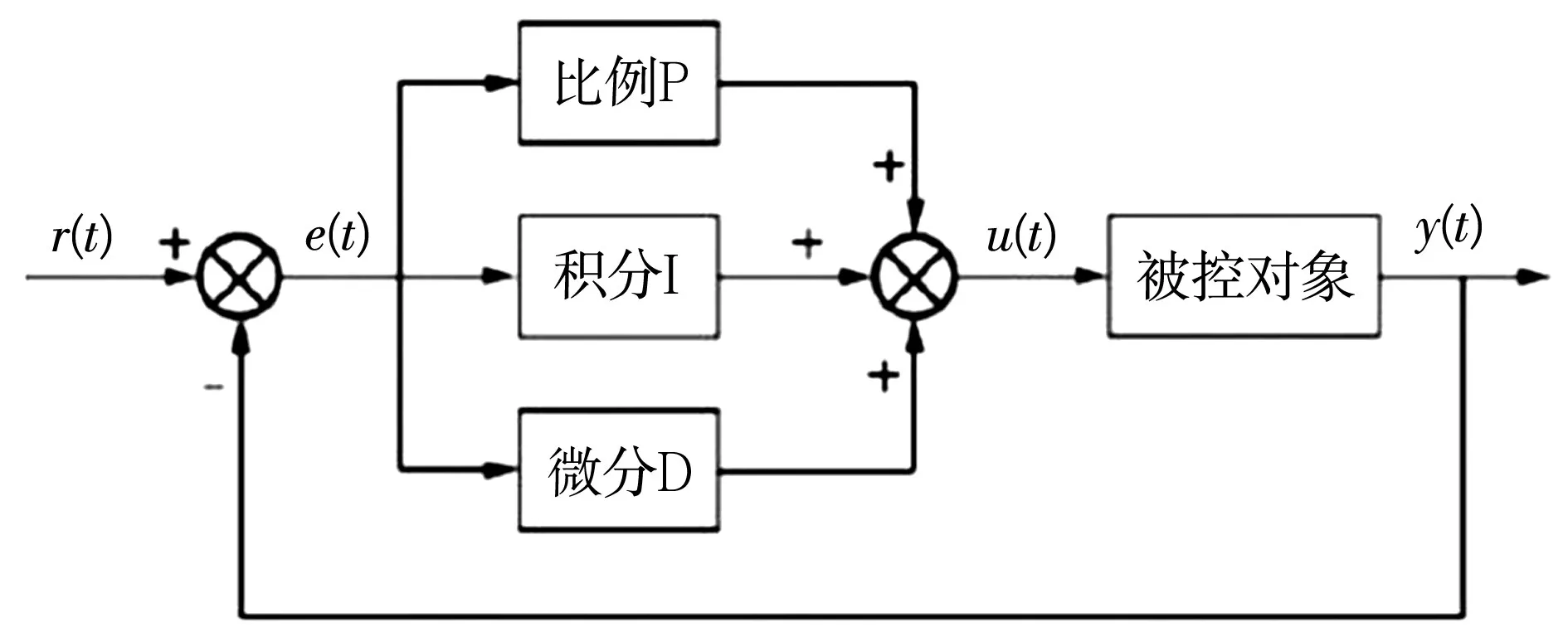
图3 普通PID控制流程

e(t)为输出和输入的偏差：

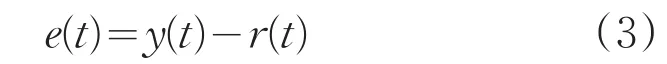
其中，r(t)为输入信号量；y(t)为输出量。

其普通PID的输出方程为可表示为：

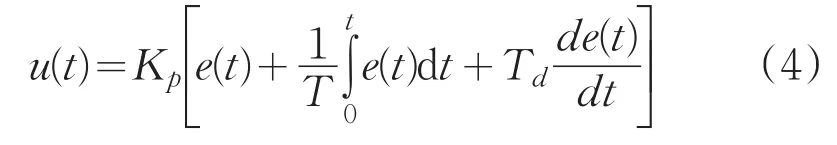
其中，Kp为比例系数；T为积分时间系数；Td为微分时间常数。

频率响应分析是在拉普拉斯域中讨论的，通过拉氏变量来分析频率特性，由于磨粒流机床的磨料是一种粘性流体，其初始压力公式为：

其中，d为被加工工件的横截面积；p为压强；γ为加工阻力系数；v为磨料缸运动速度；ρ为磨料密度；l为被抛光工件长度。

其拉氏变换为：

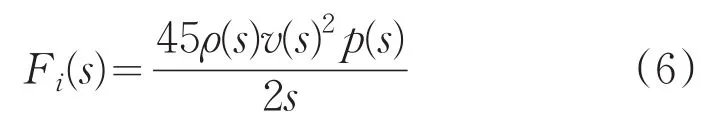
实际输出压力为：

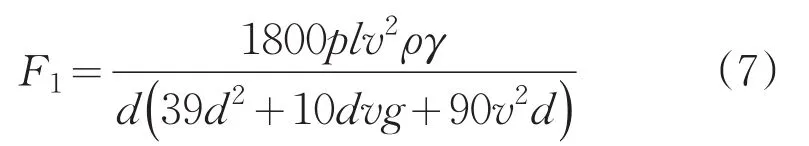
对式（7）进行拉氏变换后得到：

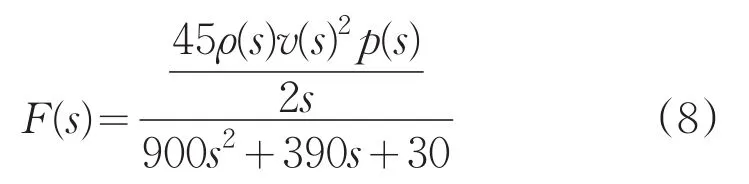
其输出压力与输入压力的拉氏变换之比为：

将S=jω代入G(s)中得到液压系统频率特性为：

根据磨粒流液压缸频率特性，磨粒流液压缸传递函数为：

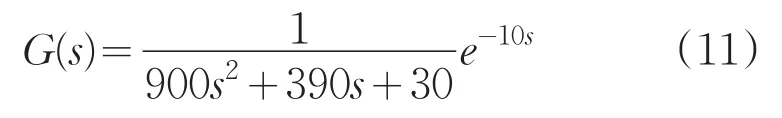
在开始加工时，系统在阶跃信号的响应下，利用MATLAB软件中的Simulink对普通PID控制器进行仿真，Simulink仿真程序如图4所示。

图4 普通PID Simulink的仿真程序

仿真结果如图5所示。通过仿真图5可以看出，普通PID算法虽能使得系统最终的输出趋于稳定，但存在超调系统响应时间缓慢和系统小幅振荡的现象，且在达到稳定状态之前，出现2次明显的振荡和3次超调现象。基于上述问题，利用遗传算法对常规的PID参数（Kp、Ki、Kd）进行优化，使系统输出达到稳定的状态。

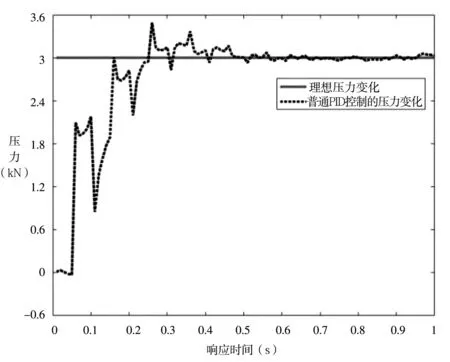
图5 普通PID控制阶跃响应曲线

2.2 遗传算法（GA）PID自整定设计

遗传算法PID自整定是将生物学原理应用到PID参数优化而形成的编码群体中，根据所选取的适配值函数，经过遗传中的复制、交叉和变异对个体进行筛选后，能够使适配值高的个体保存下来，并组成新的群体，遗传算法具有算法简单、可并行处理等特点，同时还能够得到全局最优解。将遗传算法应用到磨粒流机床液压系统的控制中，由于磨粒流机床液压缸的压力主要受液压缸电动机的转速的影响，因此液压缸电机主要采用交流伺服电机，为获得理想的动态性能，并采用误差绝对值的方法，作为最小目标函数，即：

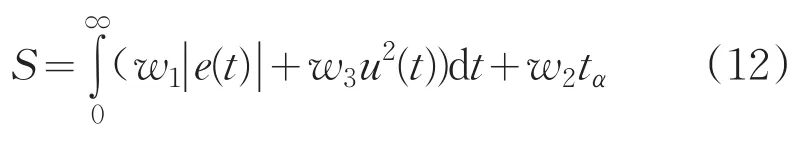
其中，e(t)为误差；u(t)为控制器输出；tα为上升时间；w1、w2、w3为权值。

系统超调量的表达式为：

其中，B为系统超调量；Y(tm)为第一个波峰值；Y(t∞)为给定值。

防止超调现象的产生，将系统超调量代入公式，即：

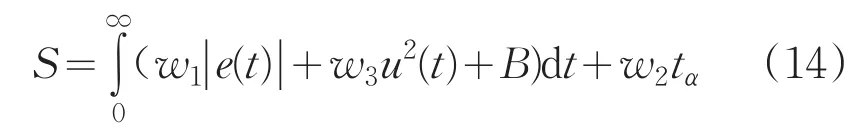
在仿真中，设置遗传算法的样本总体数50，交叉概率Pc=0.6，变异概率Pm=0.05，比例项Kp的取值范围选择0≤Kp≤10，积分项Ki取值范围选择为 0≤Ki≤1，微分项Kd取值范围选择为0≤Kd≤0.5，取w1=0.7，w2=0.003，w3=1，采用实数编码方式计算，通过150代进化获得以下优化参数为Kp=8.3741，Ki=0.093，Kd=0.2541，输入信号采用阶跃信号，经遗传算法优化后的PID控制器对磨粒流机床液压缸压力的控制如图6所示。

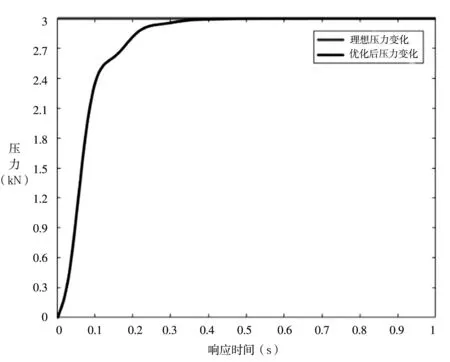
图6 遗传算法优化阶跃响应曲线

通过图6可得到，经过遗传算法优化后，系统没有明显的超调量，相比于普通PID算法有了很大的提高，系统输出较为平稳，但仍然存在系统响应时间较长的现象。为减少系统的响应时间，设计了积分分离式PID控制算法，将优化后的参数代入到积分分离式算法中，使系统在短时间内到达理想的工作状态，减少系统的响应时间。

2.3 积分分离式PID控制原理及设计

在普通的PID控制算法中，积分环节的作用是为了消除系统因其他干扰因素而产生的偏差，提高控制系统的加工精度，若系统在启动、结束过程或者系统进行大幅度增减设定时，系统会在短时间内产生较大的偏差，系统开始出现超调，甚至系统会出现剧烈的振荡现象。基于上述问题，采用积分分离式PID算法能够解决系统因其他干扰因素产生超调，积分分离式的算法基本原理为：系统在工作时，如果系统的被控制量与系统的设定值相差很大时，消除积分项对系统的控制作用；若系统的被控量在系统的设定值上下浮动或等于设定值时，加入积分项对系统的控制作用，从而达到消除偏差，提高控制精度。积分分离式算法可表示为：

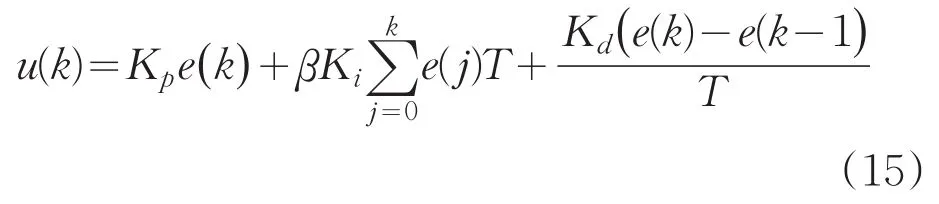
其中，T为采样时间；β为积分项开关系数；e(k)为系统偏差；e(k-1)为上一次采样偏差；Kp、Ki、Kd为比例、积分、微分项系数。

将遗传算法优化后的参数（Kp、Ki、Kd）代入到积分分离算法表达式中，即：

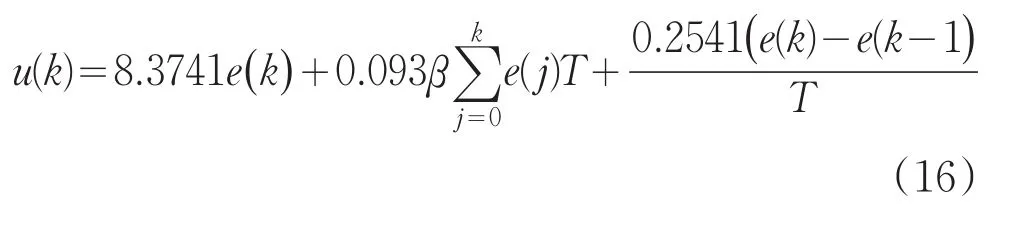
根据实际情况，设定阈值∂=0。当e(k)＜0时，β=1，引入积分作用，当e(k)≥0，β=0，取消积分作用。系统的输入信号采用阶跃信号，利用Simulink进行仿真，程序如图7所示。

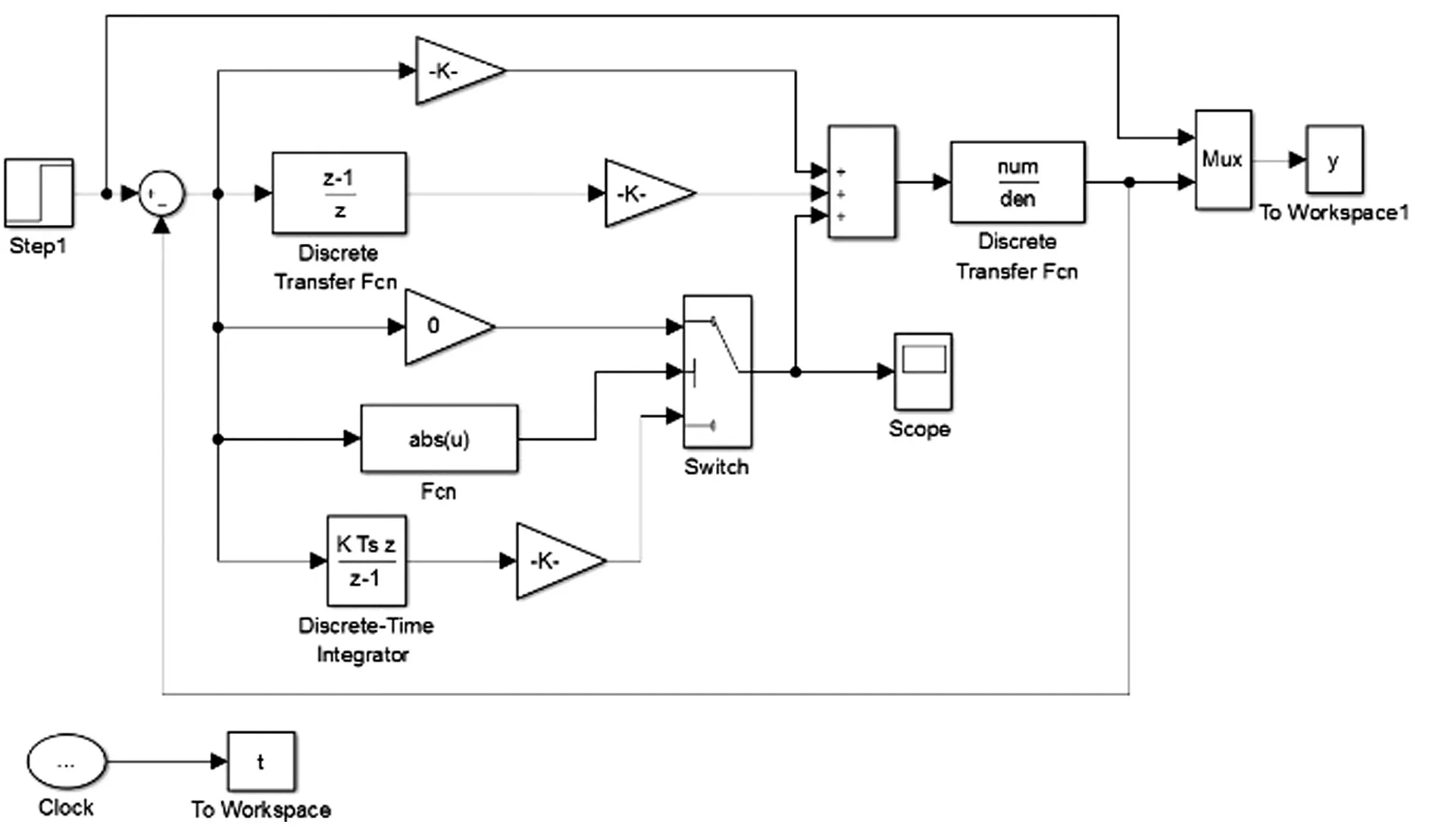
图7 积分分离Simulink仿真图

优化后的积分分离式PID算法对压力的控制结果如图8所示。

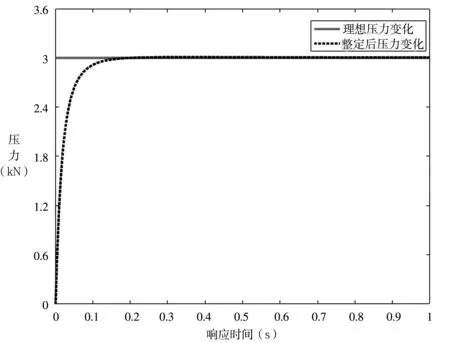
图8 基于遗传算法优化后的积分分离式PID阶跃响应

通过图8可知，经过遗传算法优化下的积分分离式阶跃响应后，系统无振荡现象产生，系统的输出更加平缓，系统的响应时间缩短了41.2%，系统响应更加迅速。无明显的超调现象，实现了在短时间内，系统能够最快的达到理想工作状态。

3 结论

本文主要以磨粒流机床液压缸压力变化为研究对象，通过比较普通PID算法、遗传算法优化、基于遗传算法优化下的积分分离式算法对液压缸压力变化的影响，利用MATLAB软件分别进行仿真，仿真结果显示，磨粒流机床液压缸控制系统采用先遗传算法优化参数，再进行积分分离式PID控制能够更好地保证系统的稳定性，系统的动态特性得到提高，超调量减小，达到稳定的时间更快，响应更加迅速，能够满足设计要求。通过仿真结果可知：

（1）三种控制方式都能最终使系统趋于稳定状态。但普通PID算法存在明显的超调量以及小幅振荡的现象。

（2）经遗传算法优化后，系统没有明显的超调量，也没有小幅振荡现象的存在。系统的输出更加平稳，但响应时间却没有很明显的变化。

（3）经遗传算法优化后的积分分离算法使系统响应速度更快，与遗传算法控制相比，其响应速度提升了41.2%。